こんにちは|こんばんは。カエルのアイコンで活動しております @kyamaz ![]() です。
です。
【はじめに】本稿の対象は次のような方を想定しております。
- 量子コンピューターや量子プログラミングに興味がある方
先日、2024/1/20にQCoderの第1回めの量子プログラミングコンテストが開催されました。このコンテストの主催者は、情報処理推進機構(IPA)の未踏ターゲット事業の2023年度採択者である雪吉さんです。IPA支援のもと開発された量子プログラミングコンテストシステム1の成果として、このたび運営が開始されたそうです。
本稿では、このコンテストで出題された問題の1つA4『Generate state $\displaystyle \frac{1}{\sqrt{3}} ( \vert 0 \rangle + \vert 1 \rangle + \vert 2 \rangle)$ I』で回答の解説にもある「制御アダマールゲート(Controlled Hadamard Gate)」について見ていきたいと思います。
2のべき乗個ではない計算基底状態の重ね合わせを作る
アダマールゲート($H := \frac{1}{\sqrt{2}} \begin{pmatrix}1 & 1 \\1 & {-1}\end{pmatrix}$)を使えば、2のべき乗個の計算基底の重ね合わせ状態は簡単に作れることは良く知られています。アダマールゲートの詳細は、@shnchrさんのHadamard(アダマール)ゲートとはどんな回転なのか?のエントリが詳しく、X基底とZ基底の変換として解説されております。
制御アダマールゲートは次のような行列で表される演算です。
$
cH =
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
0 & 0 & \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{pmatrix}
$
この演算を用いると、制御ビットの状態が$\vert 1 \rangle $の状態だけが重ね合わせの操作がされることになり、選択的に重ね合わせ状態が作れることになります。前出のコンテストの回答は次のような操作を行うことで、3つの計算基底状態の重ね合わせを作成できることが出題されました。
$\qquad
\begin{aligned}
\vert00\rangle \stackrel{H(0)}{\longrightarrow}
&\frac{1}{\sqrt{2}}(\vert00\rangle+\vert10\rangle) \\
\stackrel{cH(0,1)}{\longrightarrow}
&\frac{1}{\sqrt{2}}\vert00\rangle+\frac{1}{2}(\vert10\rangle+\vert11\rangle) \\
\stackrel{cX(1,0)}{\longrightarrow}
&\frac{1}{\sqrt{2}}\vert00\rangle+\frac{1}{2}(\vert10\rangle+\vert01\rangle)
\end{aligned}
$
Qiskitでは、制御アダマールゲートch()がライブラリで提供されています。この演算を使えば楽にプログラムがかけます。
A1の解答例
from qiskit import QuantumCircuit
def solve() -> QuantumCircuit:
qc = QuantumCircuit(2)
qc.h(0)
qc.ch(0, 1)
qc.cx(1, 0)
return qc
制御アダマールゲートを分解する
制御アダマールゲートをパウリゲート、Tゲート、CNOTゲートで表わすことを考えます。下記のサイトにヒントがあります。
ブロッホ球のy軸周りの回転(回転角は$\theta$)を
$\qquad
R_y(\beta) = \begin{pmatrix}
\cos\frac{\beta}{2} & -\sin\frac{\beta}{2} \\
\sin\frac{\beta}{2} & \cos\frac{\beta}{2}
\end{pmatrix}
$
とすると、アダマールゲート($H$)は次のように表せます。
$\qquad
H = R_y\left(\frac{\pi}{4}\right) \cdot Z \cdot R_y\left(-\frac{\pi}{4}\right)
$
ここで、
$\qquad
Z = H X H ,
R_y\left(\frac{\pi}{4}\right) = S H T H ,
R_y\left(-\frac{\pi}{4}\right) = H T^{\dagger} H S^{\dagger}
$
の関係式をつかうと、
$\begin{equation}\label{H}
H = S H T X T^{\dagger} H S^{\dagger} \tag{1}
\end{equation}$
となります。式$(\ref{H})$を検算してみてください。
$\begin{aligned}
S H T X T^{\dagger} H S^{\dagger} &= \frac{1}{2}
\begin{pmatrix} 1 & 0 \\ 0 & i \end{pmatrix}
\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}
\begin{pmatrix} 1 & 0 \\ 0 & e^{i\frac{\pi}{4}} \end{pmatrix}
\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}
\begin{pmatrix} 1 & 0 \\ 0 & e^{-i\frac{\pi}{4}} \end{pmatrix}
\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}
\begin{pmatrix} 1 & 0 \\ 0 & -i \end{pmatrix}
\\ &= \frac{1}{2}
\begin{pmatrix} 1 & 1 \\ i & -i \end{pmatrix}
\begin{pmatrix} 0 & e^{-i\frac{\pi}{4}} \\ e^{i\frac{\pi}{4}} & 0 \end{pmatrix}
\begin{pmatrix} 1 & -i \\ 1 & i \end{pmatrix}
\\ &= \frac{1}{2}
\begin{pmatrix} e^{i\frac{\pi}{4}} & e^{-i\frac{\pi}{4}} \\ e^{-i\frac{\pi}{4}} & e^{i\frac{\pi}{4}} \end{pmatrix}
\begin{pmatrix} 1 & -i \\ 1 & i \end{pmatrix}
\\ &= \frac{e^{i\frac{\pi}{4}}+e^{-i\frac{\pi}{4}}}{2}
\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}
= \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} = H
\end{aligned}$
$\begin{equation}\label{CH}
[cH] = S H T \cdot [CNOT] \cdot T^{\dagger} H S^{\dagger} \tag{2}
\end{equation}$
量子回路図で記述すると次のようになります。(※式$(\ref{CH})$とは逆順になります。)
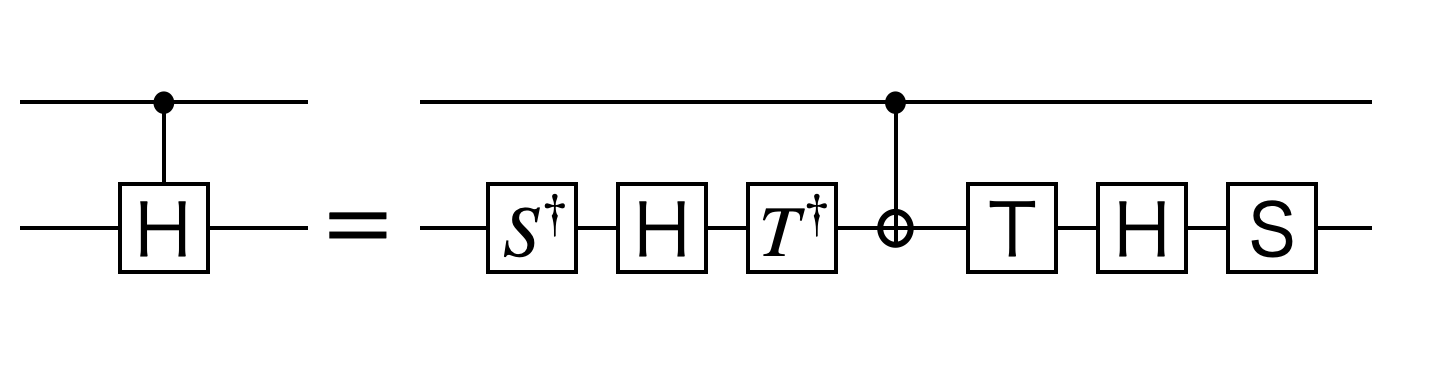
制御アダマールゲートを式$(\ref{CH})$のように、パウリゲート、Tゲート、CNOTゲートで表すことができました。
-
2023年度未踏ターゲット事業(量子コンピューティング技術を活用したソフトウェア開発分野)採択プロジェクト概要(雪吉PJ) プロジェクト名『量子プログラミングコンテストシステムの開発と量子回路シミュレータのWebAssembly化』 ↩