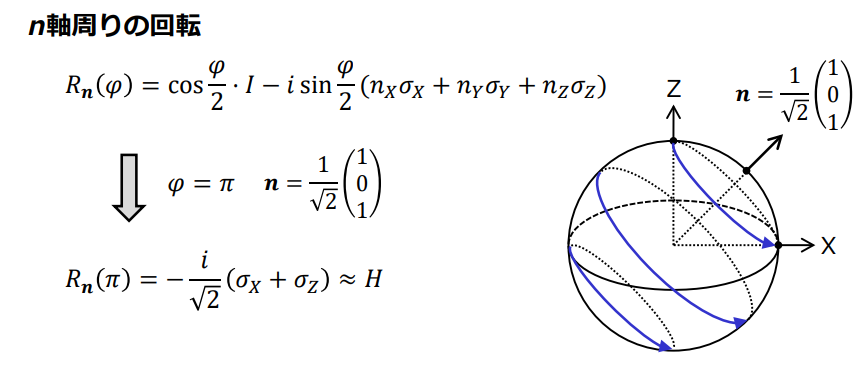この記事について
$H$(Hadamard)ゲートですが、
% basic braket
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\ketbra}[2]{\left| #1 \right\rangle \left\langle #2 \right|}
\newcommand{\ketbraket}[3]{\left| #1 \right\rangle \left\langle #2 \middle| #3 \right\rangle}
% small-size
\newcommand{\bras}[1]{\left\langle {\scriptsize #1} \right|}
\newcommand{\kets}[1]{\left| {\scriptsize #1} \right\rangle}
\newcommand{\brackets}[2]{\left\langle {\scriptsize #1} \middle| {\scriptsize #2} \right\rangle}
\newcommand{\ketbras}[2]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \right|}
\newcommand{\ketbrakets}[3]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \middle| {\scriptsize #3} \right\rangle}
% Matrix
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}
H = \frac{1}{\sqrt{2}}\mtrx{1}{1}{1}{-1}
よく知られたゲートで、重ね合わせ状態を作り出したり、
Z基底(計算基底)$\ket{0},\ket{1}$とX基底(アダマール基底)$\kets{+},\kets{-}$の行き来に利用されます。
ですが、Y基底(円基底)$\ket{i},\ket{i-}$に対して、$H$ゲートを適用すると何が起きるでしょうか?
(個人的には)予想を超える動作と$H$ゲートの実体が見えた気がしました。
ポエム的な内容ですがお付き合い頂ければと。
また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。
おさらい
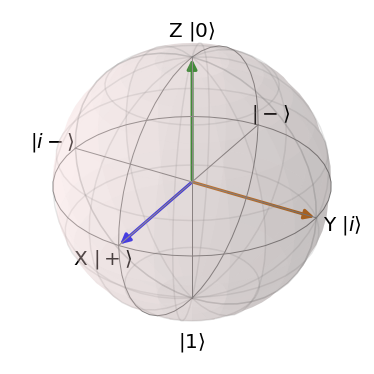
ブロッホ球と各基底
ブロッホ球上の位置関係ですが、各基底は下記のように配置されています。
Z基底、X基底でのHゲート
$Z$基底、$X$基底と$H$ゲートの関係を確認しておきましょう。
関係としては、$Z$基底と$X$基底の変換を$H$ゲートが担います。具体的には、
Z基底からX基底へは、
H\ket{0} = \frac{ \ket{0}+\ket{1} }{\sqrt{2}} = \kets{+}
\ \ \ \
H\ket{1} = \frac{ \ket{0}-\ket{1} }{\sqrt{2}} = \kets{-}
X基底からZ基底へは、
H\kets{+} = \ket{0}
\ \ \ \
H\kets{-} = \ket{1}
ブロッホ球と対応して見ていくと、下記の通りで、
- $H$ゲートによって、 $Z$軸の$\ket{0},\ket{1}$ と $X$軸の$\ket{+},\ket{-}$ の変換が行われます。
- $\pi/2(90^\circ)$回転のゲート($Ry,Y^{1/2}$)にも見えてきます。
ZとXの世界においては、上記の整理で良さそうです。
| 対応する式 | ゲート適用前 | ゲート適用後 |
|---|---|---|
| $H\ket{0}=\ket{+}$ |  |
 |
| $H\ket{+}=\ket{0}$ |  |
 |
| $H\ket{1}=\ket{-}$ |  |
 |
| $H\ket{-}=\ket{1}$ |  |
 |
HゲートとY基底
では、本題に入ります。
Y基底$\ket{i},\ket{i-}$に対して、$H$ゲートを適用するとどうなるでしょうか?
- Z-Xと同じ様に、座標軸の変換がおきるのか?
- その時の回転角は、おなじように、$\pi/2(90^\circ)$なのか?
等、確認していきたいと思います。
H|i> と H|i->の計算
計算で確認しておきたいと思います。
\ket{i} = \frac{\ket{0} + i\ket{1}}{\sqrt{2}}
\ \ \
\ket{i-} = \frac{\ket{0} - i\ket{1}}{\sqrt{2}}
ですので、$H$ゲートを適用すると、
\displaylines{
H\ket{i} = \frac{H\ket{0} + iH\ket{1}}{\sqrt{2}}
= \frac{1}{\sqrt{2}} \frac{1}{\sqrt{2}}
\left(
\ket{0} + \ket{1} + i\ket{0} - i\ket{1}
\right)
\\
= \frac{(1+i)}{2}\ket{0} + \frac{(1-i)}{2}\ket{1}
}
何やら、見慣れない式になったのですが、グローバル位相がかかっているだけで、
くくりだしてあげると、
\displaylines{
\frac{(1+i)}{2}\ket{0} + \frac{(1-i)}{2}\ket{1}
\\
=\frac{(1+i)}{2}\ket{0} -i \frac{(1+i)}{2}\ket{1}
=\frac{(1+i)}{\sqrt{2}} \times \frac{\ket{0}-i\ket{1}}{\sqrt{2}}
\\
=\frac{(1+i)}{\sqrt{2}}\ket{i-}
}
つまり、グローバル位相はかかりますが、$Y$基底においては$H$は$\ket{i} \rightarrow \ket{i-}$の反転である、$\pi(180^\circ)$回転の操作であることがわかりました。(興味深いです。)
\therefore H\ket{i} =\frac{(1+i)}{\sqrt{2}}\ket{i-}
同じ様に$H\ket{i-}$を計算すると結果としては、
H\ket{i} =\frac{(1+i)}{\sqrt{2}}\ket{i-}
\ \ \
H\ket{i-} =\frac{(1-i)}{\sqrt{2}}\ket{i}
ブロッホ球でも確認しておく
下記のとおり、$Y$基底においては、$H$ゲートは $\pi(180^\circ)$回転の操作 であることがブロッホ球でも読み取ることができます。
なお、グローバルフェーズを省略するために、下記は等号ではなく、合同記号で表現しています。
| 対応する式 | ゲート適用前 | ゲート適用後 |
|---|---|---|
| $H\ket{i} \equiv \ket{i-}$ |  |
 |
| $H\ket{i-} \equiv \ket{i}$ |  |
 |
Hを2回適用すると
上記式から自明ではありますが、
- Hを1回適用で、 $\pi(180^\circ)$回転の操作
- Hを2回適用で、 $2\pi(360^\circ)$回転の操作
となることを確認しておこうと思います。
つまり、下記の確認です。
H^2\ket{i} = \ket{i}
\ \ \
H^2\ket{i-} = \ket{i-}
ちなみに、1回適用の際にはグローバルフェーズが付きましたが、2回適用するとグローバルフェーズも含めて、状態が一致します。(つまり、合同でなく、等号となります。)
今までの結果から、$H$ゲートは、下記のように表現できます
H=\frac{(1+i)}{\sqrt{2}}\ketbra{i-}{i}
+\frac{(1-i)}{\sqrt{2}}\ketbra{i}{i-}
Hを2回適用する$H^2$を計算すると
\displaylines{
H^2=
\left(
\frac{(1+i)}{\sqrt{2}}\ketbra{i-}{i}
+\frac{(1-i)}{\sqrt{2}}\ketbra{i}{i-}
\right)^2
\\
= 0 + \frac{(1+i)(1-i)}{2}\ketbra{i-}{i-} + \frac{(1-i)(1+i)}{2}\ketbra{i}{i} + 0
\\
=\ketbra{i-}{i-} + \ketbra{i}{i}
}
よって、$H^2$では、グローバルフェーズもつかずに初期の状態に戻ることが確認できました。
\therefore H^2=\ketbra{i-}{i-} + \ketbra{i}{i}
H(Hadamard)ゲートとは
これまでの議論をまとめると、
- $ZX$基底では、相互の軸の変換を、回転角$\pi/2(90^\circ)$ で行う。
- $Y$基底では、同一軸上の変換となり、回転角$\pi(180^\circ)$ で行う。
さて、$H$ゲートの動きはブロッホ球上でどのように表現できるでしょうか?
答えは、下記の資料にありました。
上記より、引用させていただくと、
上述の説明とブロッホ球の軸のとり方が少し違うのですが、$H$ゲートは、
- Z軸とX軸の間、$45^\circ$(図中のベクトル $\mathbb{n}$)方向を中心とする回転なのです。
- この回転であれば、下記の説明が付きます。
- $H$ゲートは$ZX$基底では、相互の軸の変換を、 回転角$\pi/2(90^\circ)$ で行う。
- $H$ゲートは$Y$基底では、同一軸上の変換となり、 回転角$\pi(180^\circ)$ で行う。
まとめ
$H$ゲートの動きがブロッホ球上でご理解いただけたでしょうか?
ちょっとそれますが、$X$と$Z$に関して、下記の関係式が成り立ちます。
X = HZH
\ \ \ \ \
Z = HXH
上記であれば、ブロッホ球上の単純な回転を追えば理解できるのですが、類似の関係式で
X^{\frac{1}{2}} = V = HSH
\ \ \ \ \
Z^{\frac{1}{2}} = S = HVH
があります。
こちらの式になると、$H$ゲートの上記の様な動きを理解しないと、、、
なかなか納得できないのでは無いでしょうか?(私はそうでした)
ということで、ブロッホ球上での$H$ゲートの動きを理解頂ければ嬉しく思います。
何かあれば、コメント等、よろしければLGTMいただけると嬉しいです。