はじめに
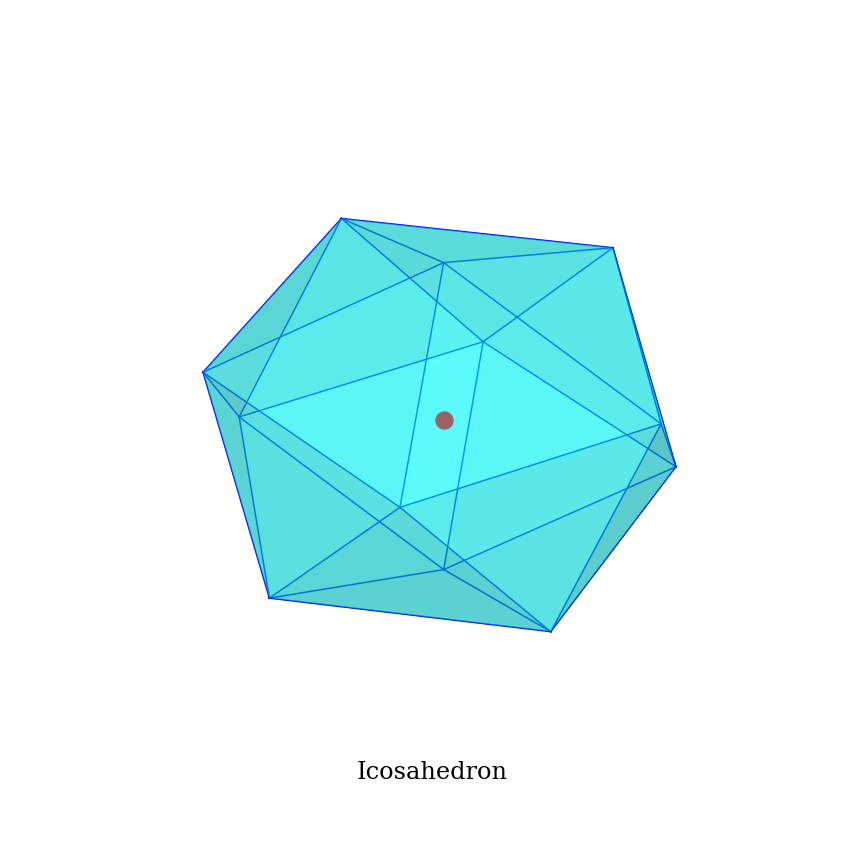
論文に載せられるレベルの綺麗な多面体の画像を、手軽に出力したいと思ったので自分でコードを書いてみました(コードを書くのは手軽じゃなかったですが笑)。
今回は、@ikiuo 様の「正多面体のデータを作る」で計算された多面体の座標などのデータを使って実際に正多面体をプロットしていきます。ただし、三角形で構成された多面体( 正四面体・正八面体・正二十体 )に限ってプロットするコードになります。正六面体と正十二面体のバージョンも時間があれば投稿します。
正多面体の描画は以下の関数で行います。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LightSource
def plot_polyhedron(ax, VERTEX, EDGE, FACET):
#グラフの描画
for i in range(len(EDGE)):
coordinates = np.array([VERTEX[EDGE[i][0]], VERTEX[EDGE[i][1]]])
x, y, z = coordinates.T
ax.plot(x, y, z,markersize=6, color='blue', linewidth=1.5)
ls = LightSource(40, 70) #光源の設定
# 面の塗りつぶし
for i in range(len(FACET)):
coordinates = np.array([VERTEX[FACET[i][0]], VERTEX[FACET[i][1]], VERTEX[FACET[i][2]]])
x, y, z = coordinates.T
ax.plot_trisurf(x, y, z, alpha=0.4, antialiased=True, shade=True,lightsource=ls, color='cyan')
# 任意の点のプロット
ax.scatter(0, 0, 0, color='red', s=300)
ax.set_axis_off() # 座標の透明化
ax.view_init(elev=40, azim=10) # 視点の設定
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
ax.set_zlim(-1, 1)
return ax
- LightSource関数について: matplotlib.colors.LightSource — Matplotlib 3.4.3 documentation
- plot_trisurf関数について:The mplot3d Toolkit — Matplotlib 3.4.3 documentation
解説
入力データ
まず、プログラムと出力結果のところから、好きな多面体のデータを丸っとコピーします。ここでは、例として正四面体の場合で行います。そのままでは使えないので、これらの配列をNumPyで扱うために修正して、以下のものを使います(データはコピペしてすぐ使える形式で最後にまとめて置いています)。
# 正四面体の情報
# 頂点
VERTEX = np.array([
[ 0. , 0. , 1. ], #0
[ 0.942809, 0. , -0.333333], #1
[-0.471405, 0.816497, -0.333333], #2
[-0.471405, -0.816497, -0.333333] #3
])
# 面と法線ベクトルと、面を構成する頂点
FACET = np.array([
[2, 0, 1], #0
[3, 0, 2], #1
[3, 1, 0], #2
[3, 2, 1] #3
])
# 辺を構成する頂点
EDGE = np.array([
[0, 1],
[1, 2],
[2, 0],
[2, 3],
[3, 0],
[3, 1]
])
Matplotlibで出力
# アスペクト比は1:1にするのがおすすめです。
fig = plt.figure(figsize = (12, 12))
ax = fig.add_subplot(1,1,1, projection='3d')
ax = plot_polyhedron(ax, VERTEX, EDGE, FACET)
ax.set_title(r"Tetrahedron", y=0.1, size=24)
plt.show()
データ置き場
コードまとめ
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LightSource
def plot_polyhedron(ax, VERTEX, EDGE, FACET):
#グラフの描画
for i in range(len(EDGE)):
coordinates = np.array([VERTEX[EDGE[i][0]], VERTEX[EDGE[i][1]]])
x, y, z = coordinates.T
ax.plot(x, y, z,markersize=6, color='blue', linewidth=1.5)
ls = LightSource(40, 70) #光源の設定
# 面の塗りつぶし
for i in range(len(FACET)):
coordinates = np.array([VERTEX[FACET[i][0]], VERTEX[FACET[i][1]], VERTEX[FACET[i][2]]])
x, y, z = coordinates.T
ax.plot_trisurf(x, y, z, alpha=0.4, antialiased=True, shade=True,lightsource=ls, color='cyan')
# 任意の点のプロット
ax.scatter(0, 0, 0, color='red', s=300)
ax.set_axis_off() # 座標の透明化
ax.view_init(elev=40, azim=10) # 視点の設定
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
ax.set_zlim(-1, 1)
return ax
# アスペクト比は1:1にするのがおすすめです。
fig = plt.figure(figsize = (12, 12))
ax = fig.add_subplot(1,1,1, projection='3d')
ax = plot_polyhedron(ax, VERTEX, EDGE, FACET)
ax.set_title(r"Tetrahedron", y=0.1, size=24)
plt.show()
正四面体の情報
# 正四面体の情報
# 頂点
VERTEX = np.array([
[ 0. , 0. , 1. ], #0
[ 0.942809, 0. , -0.333333], #1
[-0.471405, 0.816497, -0.333333], #2
[-0.471405, -0.816497, -0.333333] #3
])
# 面と法線ベクトルと、面を構成する頂点
FACET = np.array([
[2, 0, 1], #0
[3, 0, 2], #1
[3, 1, 0], #2
[3, 2, 1] #3
])
# 辺を構成する頂点
EDGE = np.array([
[0, 1],
[1, 2],
[2, 0],
[2, 3],
[3, 0],
[3, 1]
])
正八面体の情報
# 正八面体の情報
VERTEX= np.array([
[ 0., 0., 1.], #0
[ 1., 0., 0.], #1
[ 0., 1., 0.], #2
[-1., 0., 0.], #3
[-0., -1., 0.], #4
[ 0., -0., -1.] #5
])
FACET = np.array([
[2, 0, 1], #0
[3, 0, 2], #1
[4, 0, 3], #2
[4, 1, 0], #3
[5, 1, 4], #4
[5, 2, 1], #5
[5, 3, 2], #6
[5, 4, 3] #7
])
EDGE = np.array([
[0, 1],
[1, 2],
[2, 0],
[2, 3],
[3, 0],
[3, 4],
[4, 0],
[4, 1],
[4, 5],
[5, 1],
[5, 2],
[5, 3]
])
正二十面体の情報
# 正二十面体の情報
VERTEX = np.array([ #12
[ +0.000000, +0.000000, +1.000000 ], #0
[ +0.894427, +0.000000, +0.447214 ], #1
[ +0.276393, +0.850651, +0.447214 ], #2
[ -0.723607, +0.525731, +0.447214 ], #3
[ -0.723607, -0.525731, +0.447214 ], #4
[ +0.276393, -0.850651, +0.447214 ], #5
[ +0.723607, -0.525731, -0.447214 ], #6
[ +0.723607, +0.525731, -0.447214 ], #7
[ -0.276393, +0.850651, -0.447214 ], #8
[ -0.894427, -0.000000, -0.447214 ], #9
[ -0.276393, -0.850651, -0.447214 ], #10
[ -0.000000, +0.000000, -1.000000 ], #11
])
FACET = np.array([ #20
( +0.491123, +0.356822, +0.794654 ), ( 2, 0, 1 ), #0
( -0.187592, +0.577350, +0.794654 ), ( 3, 0, 2 ), #1
( -0.607062, +0.000000, +0.794654 ), ( 4, 0, 3 ), #2
( -0.187592, -0.577350, +0.794654 ), ( 5, 0, 4 ), #3
( +0.491123, -0.356822, +0.794654 ), ( 5, 1, 0 ), #4
( +0.794654, -0.577350, +0.187592 ), ( 6, 1, 5 ), #5
( +0.982247, -0.000000, -0.187592 ), ( 7, 1, 6 ), #6
( +0.794654, +0.577350, +0.187592 ), ( 7, 2, 1 ), #7
( +0.303531, +0.934172, -0.187592 ), ( 8, 2, 7 ), #8
( -0.303531, +0.934172, +0.187592 ), ( 8, 3, 2 ), #9
( -0.794654, +0.577350, -0.187592 ), ( 9, 3, 8 ), #10
( -0.982247, -0.000000, +0.187592 ), ( 9, 4, 3 ), #11
( -0.794654, -0.577350, -0.187592 ), ( 10, 4, 9 ), #12
( -0.303531, -0.934172, +0.187592 ), ( 10, 5, 4 ), #13
( +0.303531, -0.934172, -0.187592 ), ( 10, 6, 5 ), #14
( +0.187592, -0.577350, -0.794654 ), ( 11, 6, 10 ), #15
( +0.607062, +0.000000, -0.794654 ), ( 11, 7, 6 ), #16
( +0.187592, +0.577350, -0.794654 ), ( 11, 8, 7 ), #17
( -0.491123, +0.356822, -0.794654 ), ( 11, 9, 8 ), #18
( -0.491123, -0.356822, -0.794654 ), ( 11, 10, 9 ), #19
])
EDGE = np.array([
[ 0, 1], [ 1, 2], [ 2, 0], [ 2, 3],
[ 3, 0], [ 3, 4], [ 4, 0], [ 4, 5],
[ 5, 0], [ 5, 1], [ 5, 6], [ 6, 1],
[ 6, 7], [ 7, 1], [ 7, 2], [ 7, 8],
[ 8, 2], [ 8, 3], [ 8, 9], [ 9, 3],
[ 9, 4], [ 9, 10], [ 10, 4], [ 10, 5],
[ 10, 6], [ 10, 11], [ 11, 6], [ 11, 7],
[ 11, 8], [ 11, 9],
])
FACET=FACET[1::2].astype(int)
References
