概要
なんかカレンダーイベントやってるのでその「波」に乗じて学部時代の授業でやった「波」のシミュレーションで改めて遊んでみようと思い立ちました。
数値計算が主ですので細かい差分法などの紹介は省き、簡単に数式と差分解法の結果を載せて実装に移ります。
ちなみに全くの素人ですので、細かい話や難しい話はできませんししないのでご了承ください。また間違いも散見されるかと思いますので、発見したらご指摘よろしくお願いします。
以下のコードは全てMacのターミナル上で実行しています。
jupyter notebookなどを使用する場合はセルの先頭に
%matplotlib nbagg
をつければOKなはずです。
目次
波動方程式
波動方程式は「波」を記述する方程式の一つです。例えば皆さんもシュレーディンガー方程式の名前くらいは聞いたことがありませんかね〜そのシュレーディンガー方程式も波動方程式の一種です。
シュレーディンガー方程式は粒子などの運動を記述する方程式です。皆さんも知っての通り物質は実態のあるモノとして見て触れて感じることができますが、粒子レベルのミクロな世界では物質と波動の境界線は曖昧になり、電子などは波としてしか計算することができません。
このようにいろいろと「波」に関する方程式を記述しているため、例えばマクロ世界における弦の振動や膜の振動も波動方程式で表すことができます。
そんな波動方程式の数値計算で遊んでみたいと思います。
1次元波動方程式
まずは1次元、弦のシミュレーションです。
\rho \cfrac{\partial^2 y}{\partial t^2} = T \cfrac{\partial^2 y}{\partial x^2} - k \cfrac{\partial y}{\partial t} \\
\Leftrightarrow \rho y_{tt} = T y_{xx} - k y_t
$\rho$は線密度、$T$は張力、$k$は減衰率を表しています。
この偏微分方程式を
\begin{align}
\cfrac{\partial^2 y}{\partial t^2} &= \cfrac{y^{(n+1)}_j - 2y^{(n)}_j + y^{(n-1)}_j}{\Delta t^2} \\
\cfrac{\partial^2 y}{\partial x^2} &= \cfrac{y^{(n)}_{j+1} - 2y^{(n)}_j + y^{(n)}_{j-1}}{\Delta x^2} \\
\cfrac{\partial y}{\partial t} &= \cfrac{y^{(n)}_j - y^{(n-1)}_j}{\Delta t}
\end{align}
のようにして差分方程式を作ります。
y^{(n+1)}_j = 2y^{(n)}_j - y^{(n-1)}_j + \cfrac{T}{\rho} \cfrac{\Delta t^2}{\Delta x^2} \left( y^{(n)}_{j+1} - 2y^{(n)}_j + y^{(n)}_{j-1} \right) - \cfrac{k}{\rho} \Delta t \left( y^{(n)}_j - y^{(n-1)}_j \right)
なお、境界条件は固定端(ディリクレ境界条件)、初期条件は$y^{(0)} = \sin \pi x$としています。
y_0 = y_n = 0
実験コード
import sys
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as anim
def is_float(value):
try:
float(value)
except ValueError:
return False
else:
return True
def get_params():
"""Get parameters from command prompt."""
kwds = {}
kwds["Nx"] = 100
kwds["Nt"] = 10000
kwds["x_range"] = 1.0
kwds["y_range"] = 0.0125
kwds["t_range"] = 1.0
kwds["rho"] = 1e-2
kwds["tension"] = 1.0
kwds["decay"] = 0.0
kwds["frames"] = 64
kwds["interval"] = 100
kwds["title"] = "1D-wave"
kwds["fps"] = 10
opts = sys.argv[1:]
for opt in opts:
key, value = opt.split("=")
if value.isdecimal():
value = int(value)
elif is_float(value):
value = float(value)
kwds[key] = value
return kwds
def _cal_next(i, y, t, n, Nx, ratio, decay, dt, y_max):
for j in range(1, Nx):
y[n+1, j] = (2*y[n, j] - y[n-1, j]
+ ratio*(y[n, j+1] - 2*y[n, j] + y[n, j-1])
- decay*dt*(y[n, j] - y[n-1, j]))
y[n-1] = y[n].copy()
y[n] = y[n+1].copy()
if np.max(y[n+1]) > 1.1*y_max or np.min(y[n+1]) < -1.1*y_max:
print("Overflow will occur.")
print("t = {}".format(t[i]))
sys.exit(1)
if np.any(np.isnan(y[n+1])):
print("Not a number has come.")
print("t = {}".format(t[i]))
sys.exit(1)
return y
def init(x, y_range, n):
return np.tile(y_range*np.sin(np.pi*x), reps=(n+2, 1))
def update(i, frames, y, x, t, n, Nx, Nt, ratio, decay, dt, y_max):
plt.cla()
for j in range(int(i/frames*Nt), int((i+1)/frames*Nt)):
per = int((j+1)/Nt*50)
bar = "/"*per + " "*(50 - per)
print("\r[{}]".format(bar), end="")
y = _cal_next(j, y, t, n, Nx, ratio, decay, dt, y_max)
plt.ylim(1.1*y_max, -1.1*y_max)
plt.plot(x, y[n], "c")
plt.title("t={}".format(np.round(t[int((i+1)/frames*Nt)], 3)))
def wave_plot(x_range=0.0, t_range=0.0, y_range=0.0, Nx=0, Nt=0,
rho=0.0, decay=0.0, tension=0.0,
frames=0, interval=0, title="", fps=0):
n = 1
x = np.linspace(0.0, x_range, Nx+1)
t = np.linspace(0.0, t_range, Nt+1)
y = init(x, y_range, n)
y_max = np.max(y)
dx = x[1] - x[0]
dt = t[1] - t[0]
c = np.sqrt(tension/rho)
decay /= rho
ratio = (c*dt/dx)**2
print("check values")
print("\t dx = {},\t dt = {}".format(dx, dt))
print("\tdecay = {},\tc={}".format(decay, c))
print("\tratio = {}".format(ratio))
args = (frames,y, x, t, n, Nx, Nt, ratio, decay, dt, y_max)
fig = plt.figure()
ani = anim.FuncAnimation(fig, update, fargs=args,
frames=frames, interval=interval)
ani.save(title+".gif", writer="pillow", fps=fps)
if __name__ == "__main__":
kwds = get_params()
wave_plot(**kwds)
$ python wave_1d.py (オプション)
| オプション | 説明 |
|---|---|
| Nx | x軸方向の分割数 |
| Nt | 時間方向の分割数 |
| x_range | x軸方向の長さ |
| y_range | y軸方向の範囲 |
| t_range | 時間方向の長さ |
| rho | 線密度 |
| tension | 張力 |
| decay | 減衰率 |
| frames | GIFの枚数 |
| interval | GIFの間隔 |
| title | GIFのタイトル |
| fps | GIFのFPS |
$ python wave_1d.py decay=0.125
def init(x, y_range, n):
#return np.tile(y_range*np.sin(np.pi*x), reps=(n+2, 1))
return np.tile(y_range*x*np.log(x+0.01), reps=(n+2, 1))
$ python wave_1d.py rho=0.1 tension=3
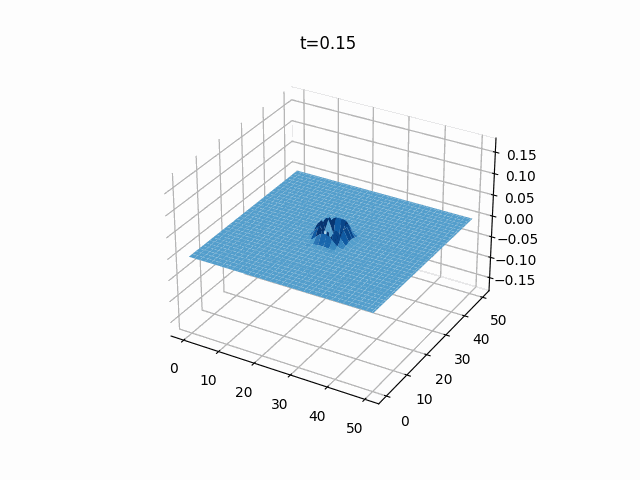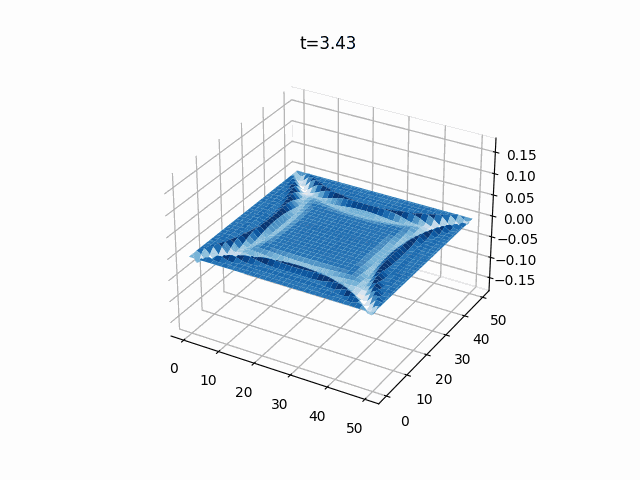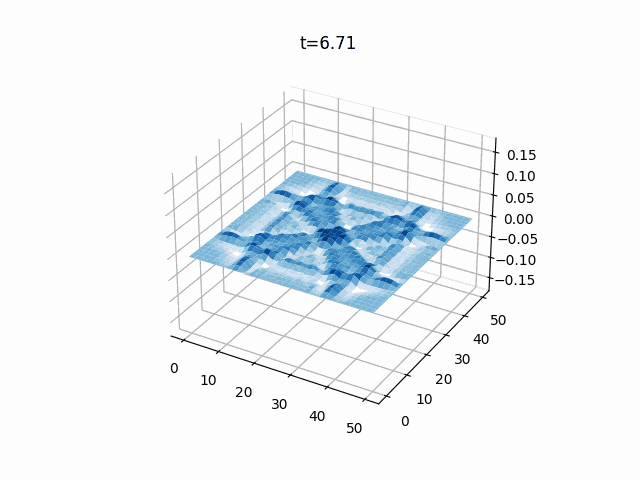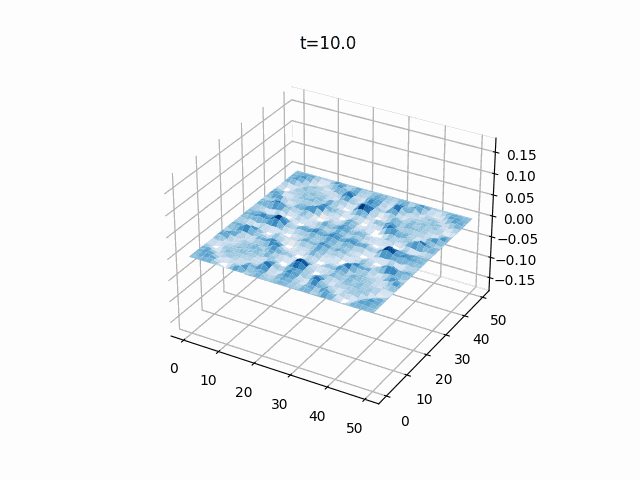
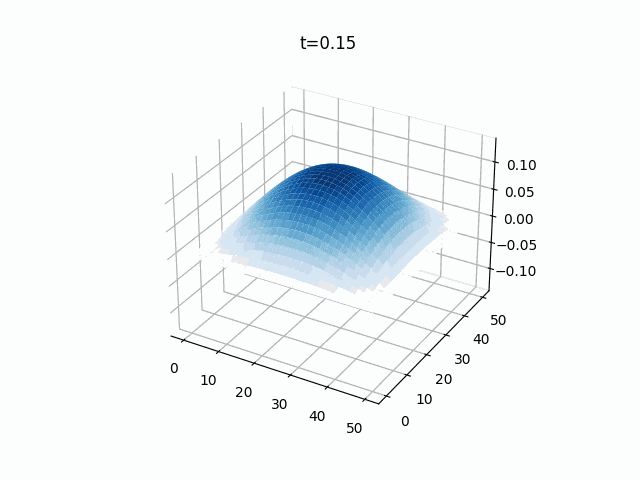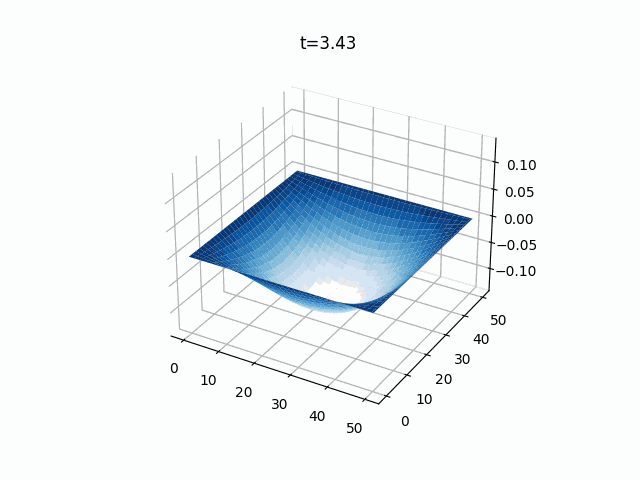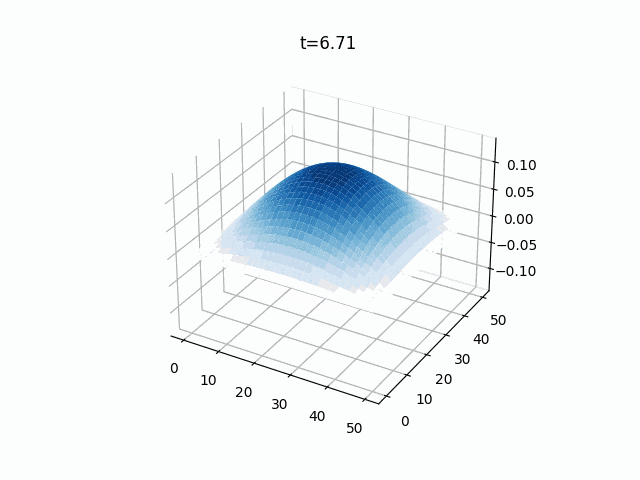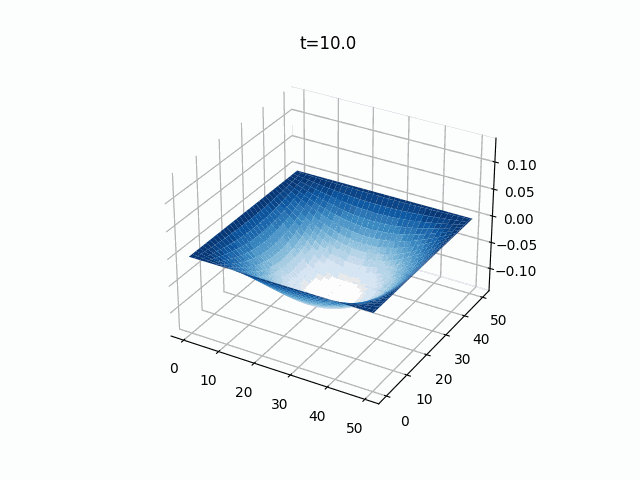
2次元波動方程式
こちらは2次元の膜のシミュレーションです。
\begin{align}
\rho \cfrac{\partial^2 z}{\partial t^2} &= T \left( \cfrac{\partial^2 z}{\partial x^2} + \cfrac{\partial^2 z}{\partial y^2} \right) - k \cfrac{\partial z}{\partial t} \\
\rho z_{tt} &= T (z_{xx} + z_{yy}) - k z_t
\end{align}
変数やらは1次元波動方程式と同じです。この偏微分方程式を同じように
\begin{align}
\cfrac{\partial^2 z}{\partial t^2} &= \cfrac{z^{(n+1)}_{j, k} - 2z^{(n)}_{j, k} + z^{(n-1)}_{j, k}}{\Delta t^2} \\
\cfrac{\partial^2 z}{\partial x^2} &= \cfrac{z^{(n)}_{j+1, k} - 2z^{(n)}_{j, k} + z^{(n)}_{j-1, k}}{\Delta x^2} \\
\cfrac{\partial^2 z}{\partial y^2} &= \cfrac{z^{(n)}_{j, k+1} - 2z^{(n)}_{j, k} + z^{(n)}_{j, k-1}}{\Delta y^2} \\
\cfrac{\partial z}{\partial t} &= \cfrac{z^{(n)}_{j, k} - z^{(n-1)}_{j, k}}{\Delta t}
\end{align}
とすることで差分方程式を作ります。
z^{(n+1)}_{j, k} = 2z^{(n)}_{j, k} - z^{(n-1)}_{j, k} + \cfrac{T}{\rho} \left\{ \cfrac{\Delta t^2}{\Delta x^2} \left( z^{(n)}_{j+1, k} - 2z^{(n)}_{j, k} + z^{(n)}_{j-1, k} \right) + \cfrac{\Delta t^2}{\Delta y^2} \left( z^{(n)}_{j, k+1} - 2z^{(n)}_{j, k} + z^{(n)}_{j, k-1} \right) \right\} - \cfrac{k}{\rho} \Delta t \left( z^{(n)}_{j, k} - z^{(n-1)}_{j, k} \right)
境界条件は先ほどと同じく固定端(ディリクレ境界条件)で、初期値は2次元ガウス分布
z^{(0)} = \frac{1}{\sqrt{(2\pi)^2 |\boldsymbol{\sigma}|}} \exp \left\{ -\frac{1}{2}(\boldsymbol{x} - \boldsymbol{\mu})^{\top} \boldsymbol{\sigma}^{-1} (\boldsymbol{x} - \boldsymbol{\mu}) \right\} \\
\boldsymbol{x} = \left( \begin{array}[c]
xx_1 \\
x_2
\end{array} \right), \qquad
\boldsymbol{\mu} = \left( \begin{array}[c]
m\mu_{x_1} \\
\mu_{x_2}
\end{array} \right), \qquad
\boldsymbol{\sigma} = \left( \begin{array}[cc]
s\sigma_{x_1}^2 & \sigma_{x_1 x_2} \\
\sigma_{x_2 x_1} & \sigma_{x_2}^2
\end{array} \right)
実験コード
import sys
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as anim
from mpl_toolkits.mplot3d import Axes3D
from scipy.stats import multivariate_normal
def is_float(value):
try:
float(value)
except ValueError:
return False
else:
return True
def get_params():
"""Get parameters from command prompt."""
kwds = {}
kwds["Nx"] = 100
kwds["Ny"] = 100
kwds["Nt"] = 1000
kwds["x_range"] = 50.0
kwds["y_range"] = 50.0
kwds["z_range"] = 0.125
kwds["t_range"] = 10.0
kwds["x_center"] = 0.5*kwds["x_range"]
kwds["y_center"] = 0.5*kwds["y_range"]
kwds["rho"] = 1e-2
kwds["tension"] = 1.0
kwds["decay"] = 0.0
kwds["frames"] = 64
kwds["interval"] = 100
kwds["title"] = "2D-wave"
kwds["fps"] = 10
opts = sys.argv[1:]
for opt in opts:
key, value = opt.split("=")
if value.isdecimal():
value = int(value)
elif is_float(value):
value = float(value)
kwds[key] = value
return kwds
def _cal_next(i, z, t, n, Nx, Ny, ratio_x, ratio_y, decay, dt, z_max):
for j in range(1, Nx):
for k in range(1, Ny):
z[n+1, j, k] = (2*z[n, j, k] - z[n-1, j, k]
+ ratio_x*(z[n, j+1, k] - 2*z[n, j, k] + z[n, j-1, k])
+ ratio_y*(z[n, j, k+1] - 2*z[n, j, k] + z[n, j, k-1])
- decay*dt*(z[n, j, k] - z[n-1, j, k]))
z[n-1] = z[n].copy()
z[n] = z[n+1].copy()
if np.max(z[n+1]) > 1.1*z_max or np.min(z[n+1]) < -1.1*z_max:
print("Overflow will occur.")
print("t = {}".format(t[i]))
sys.exit(1)
if np.any(np.isnan(z[n+1])):
print("Not a number has come.")
print("t = {}".format(t[i]))
sys.exit(1)
return z
def init(x, y, z_range, n, x_center, y_center):
mu = np.array([x_center, y_center])
sigma = np.array([[1, 0], [0, 1]])
pos = np.dstack((x, y))
return np.tile(multivariate_normal(mu, sigma).pdf(pos), (n+2, 1, 1))
def update(i, ax, frames, z, x, y, t, n, Nx, Ny, Nt,
ratio_x, ratio_y, decay, dt, z_max):
for j in range(int(i/frames*Nt), int((i+1)/frames*Nt)):
per = int((j+1)/Nt*50)
bar = "/"*per + " "*(50 - per)
print("\r[{}]".format(bar), end="")
z = _cal_next(i, z, t, n, Nx, Ny, ratio_x, ratio_y, decay, dt, z_max)
ax.cla()
ax.set_zlim(-1.1*z_max, 1.1*z_max)
ax.plot_surface(x, y, z[n], cmap="Blues")
ax.set_title("t={}".format(np.round(t[int((i+1)/frames*Nt)], 3)))
def wave_plot(x_range=0.0, y_range=0.0, z_range=0.0, t_range=0.0,
x_center=0.0, y_center=0.0, Nx=0, Ny=0, Nt=0,
rho=0.0, decay=0.0, tension=0.0,
frames=0, interval=0, title="", fps=0):
n = 1
x = np.linspace(0.0, x_range, Nx+1)
y = np.linspace(0.0, y_range, Ny+1)
t = np.linspace(0.0, t_range, Nt+1)
dx = x[1] - x[0]
dy = y[1] - y[0]
dt = t[1] - t[0]
x, y = np.meshgrid(x, y)
z = init(x, y, z_range, n, x_center, y_center)
z_max = np.max(z)
c = np.sqrt(tension/rho)
decay /= rho
ratio_x = (c*dt/dx)**2
ratio_y = (c*dt/dy)**2
print("check values")
print("\t dx = {},\t dy = {},\t dt = {}".format(dx, dy, dt))
print("\tdecay = {},\tc={}".format(decay, c))
print("\tratio_x = {},\t ratio_y = {}".format(ratio_x, ratio_y))
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
args = (ax, frames, z, x, y, t, n, Nx, Ny, Nt,
ratio_x, ratio_y, decay, dt, z_max)
ani = anim.FuncAnimation(fig, update, fargs=args,
frames=frames, interval=interval)
ani.save(title+".gif", writer="pillow", fps=fps)
if __name__ == "__main__":
kwds = get_params()
wave_plot(**kwds)
$ python wave_2d.py (オプション)
| オプション | 説明 |
|---|---|
| Nx | x軸方向の分割数 |
| Ny | y軸方向の分割数 |
| Nt | 時間方向の分割数 |
| x_range | x軸方向の長さ |
| y_range | y軸方向の長さ |
| z_range | z軸方向の範囲 |
| t_range | 時間方向の長さ |
| x_center | 2次元ガウス分布のx軸中心(平均値) |
| y_center | 2次元ガウス分布のy軸中心(平均値) |
| rho | 面密度 |
| tension | 張力 |
| decay | 減衰率 |
| frames | GIFの枚数 |
| interval | GIFの間隔 |
| title | GIFのタイトル |
| fps | GIFのFPS |
$ python wave_2d.py decay=25e-3
え?膜っぽくないって?そんな時はinit関数を次のように変更してください。膜っぽくなります。
z^{(0)} = \sin \left( \pi * \cfrac{x}{\max x} \right) \sin \left( \pi * \cfrac{y}{\max y} \right)
def init(x, y, z_range, n, x_center, y_center):
return np.tile(z_range*np.sin(np.pi*x/np.max(x))*np.sin(np.pi*y/np.max(y)), (n+2, 1, 1))
Burgers方程式
続いて衝撃波の方程式らしいBurgers方程式の数値解析です。いまだにどうしてこれが衝撃波方程式なのかわかっていません...
\begin{align}
\cfrac{\partial y}{\partial t} + y \cfrac{\partial y}{\partial x} & = \nu \cfrac{\partial^2 y}{\partial x^2} \\
y_t + y y_x &= \nu y_{xx}
\end{align}
$\nu$は動的粘性率と呼ばれる粘性を表す項になります。
これを
\begin{align}
\cfrac{\partial y}{\partial t} &= \cfrac{y^{(n+1)}_j - y^{(n)}_j}{\Delta t} \\
\cfrac{\partial y}{\partial x} &= \cfrac{y^{(n)}_j - y^{(n)}_{j-1}}{\Delta x} \\
\cfrac{\partial^2 y}{\partial x^2} &= \cfrac{y^{(n)}_{j+1} - 2y^{(n)}_j + y^{(n)}_{j-1}}{\Delta x^2}
\end{align}
として、
y^{(n+1)}_j = y^{(n)}_j - \cfrac{\Delta t}{\Delta x} y^{(n)}_j \left( y^{(n)}_j - y^{(n)}_{j-1} \right) + \nu \cfrac{\Delta t}{\Delta x^2} \left( y^{(n)}_{j+1} - 2y^{(n)}_j + y^{(n)}_{j-1} \right)
とすることで差分方程式を作ります。
境界条件を固定端、初期値を$\sin \pi x$として数値計算を行うと次のようになります。
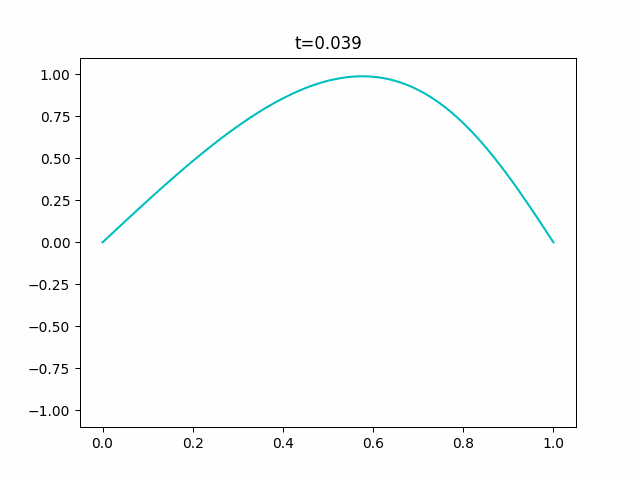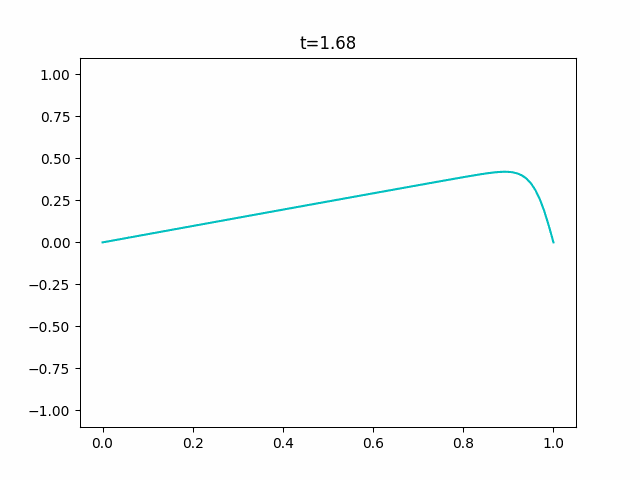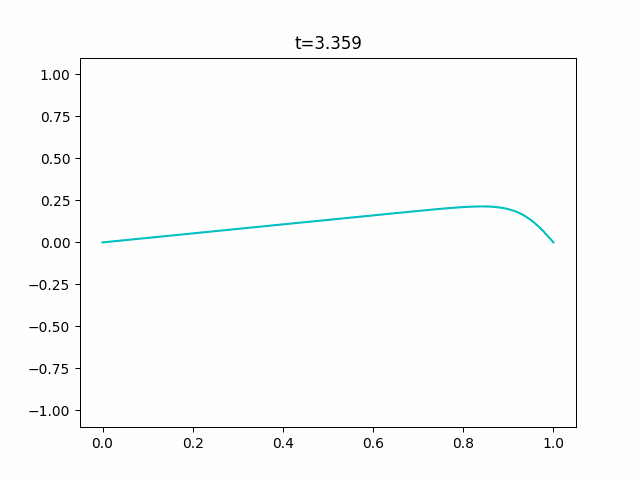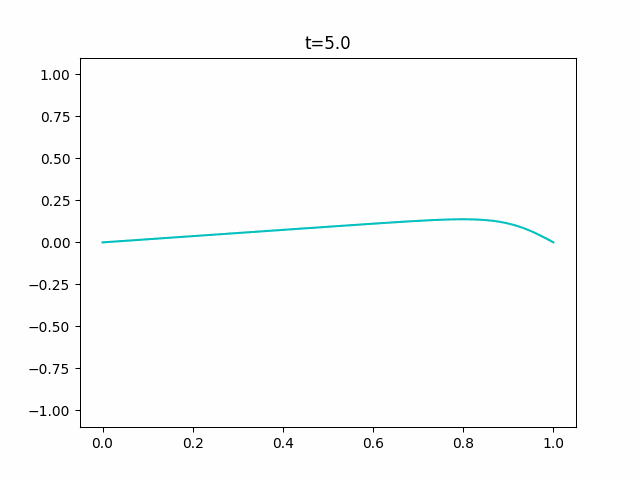
実験コード
import sys
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as anim
def is_float(value):
try:
float(value)
except ValueError:
return False
else:
return True
def get_params():
"""Get parameters from command prompt."""
kwds = {}
kwds["Nx"] = 100
kwds["Nt"] = 10000
kwds["x_range"] = 1.0
kwds["y_range"] = 0.125
kwds["t_range"] = 5.0
kwds["v"] = 0.01
kwds["frames"] = 128
kwds["interval"] = 100
kwds["title"] = "burgers"
kwds["fps"] = 20
opts = sys.argv[1:]
for opt in opts:
key, value = opt.split("=")
if value.isdecimal():
value = int(value)
elif is_float(value):
value = float(value)
kwds[key] = value
return kwds
def _cal_next(i, y, t, n, Nx, ratio1, ratio2, y_max):
for j in range(1, Nx):
y[n+1, j] = (y[n, j] - ratio1*y[n, j]*(y[n, j] - y[n, j-1])
+ ratio2*(y[n, j+1] - 2*y[n, j] + y[n, j-1]))
y[n] = y[n+1].copy()
if np.max(y[n+1]) > 1.1*y_max or np.min(y[n+1]) < -1.1*y_max:
print("Overflow will occur.")
print("t = {}".format(t[i]))
sys.exit(1)
if np.any(np.isnan(y[n+1])):
print("Not a number has come.")
print("t = {}".format(t[i]))
sys.exit(1)
return y
def init(x, y_range, n):
return np.tile(np.sin(np.pi*x), (n+2, 1))
def update(i, frames, y, x, t, n, Nx, Nt, ratio1, ratio2, dt, y_max):
for j in range(int(i/frames*Nt), int((i+1)/frames*Nt)):
per = int((j+1)/Nt*50)
bar = "/"*per + " "*(50 - per)
print("\r[{}]".format(bar), end="")
y = _cal_next(j, y, t, n, Nx, ratio1, ratio2, y_max)
plt.cla()
plt.ylim(-1.1*y_max, 1.1*y_max)
plt.plot(x, y[n], "c")
plt.title("t={}".format(np.round(t[int((i+1)/frames*Nt)], 3)))
def wave_plot(x_range=0.0, t_range=0.0, y_range=0.0, Nx=0, Nt=0,
v=0.0, frames=0, interval=0, title="", fps=0):
n = 0
x = np.linspace(0.0, x_range, Nx+1)
t = np.linspace(0.0, t_range, Nt+1)
y = init(x, y_range, n)
y_max = np.max(y)
dx = x[1] - x[0]
dt = t[1] - t[0]
ratio1 = dt/dx
ratio2 = v*dt/dx**2
print("check values")
print("\t dx = {},\t dt = {}".format(dx, dt))
print("\tratio1 = {},\tratio2 = {}".format(ratio1, ratio2))
args = (frames, y, x, t, n, Nx, Nt, ratio1, ratio2, dt, y_max)
fig = plt.figure()
ani = anim.FuncAnimation(fig, update, fargs=args,
frames=frames, interval=interval)
ani.save(title+".gif", writer="pillow", fps=fps)
if __name__ == "__main__":
kwds = get_params()
wave_plot(**kwds)
$ python burgers.py (オプション)
| オプション | 説明 |
|---|---|
| Nx | x軸方向の分割数 |
| Nt | 時間方向の分割数 |
| x_range | x軸方向の長さ |
| y_range | y軸方向の範囲 |
| t_range | 時間方向の長さ |
| v | 動的粘性率($\nu$の代わりに$v$を使用しています。) |
| frames | GIFの枚数 |
| interval | GIFの間隔 |
| title | GIFのタイトル |
| fps | GIFのFPS |
KdV方程式
続いて孤立波(ソリトン)で有名なKdV方程式を紹介します。
\begin{align}
\cfrac{\partial y}{\partial t} + y \cfrac{\partial y}{\partial x} + \delta^2 \cfrac{\partial^3 y}{\partial x^3} &= 0 \\
y_t + y y_x + \delta^2 y_{xxx} &= 0
\end{align}
これをZabuskyとKruskalの論文にある差分式を利用して
y^{(n+1)}_j = \left\{ \begin{align}
y^{(n)}_j - 0.5 \times \cfrac{\Delta t}{3 \Delta x} \left( y^{(n)}_{j+1} + y^{(n)}_j + y^{(n)}_{j-1} \right) \left( y^{(n)}_{j+1} - y^{(n)}_{j-1} \right) - 0.5 \times \cfrac{\Delta t}{\Delta x^3} \left( y^{(n)}_{j+2} - 2y^{(n)}_{j+1} + 2y^{(n)}_{j-1} - y^{(n)}_{j-2} \right) && (n = 0) \\
y^{(n)}_j - \cfrac{\Delta t}{3 \Delta x} \left( y^{(n)}_{j+1} + y^{(n)}_j + y^{(n)}_{j-1} \right) \left( y^{(n)}_{j+1} - y^{(n)}_{j-1} \right) - \cfrac{\Delta t}{\Delta x^3} \left( y^{(n)}_{j+2} - 2y^{(n)}_{j+1} + 2y^{(n)}_{j-1} - y^{(n)}_{j-2} \right) && (n \ge 1)
\end{align} \right.
とすることで数値計算ができるようになります。
境界条件に周期境界条件を用いて、初期値を$y^{(0)} = \cos 2 \pi x$とすると次のようなGIFが得られます。
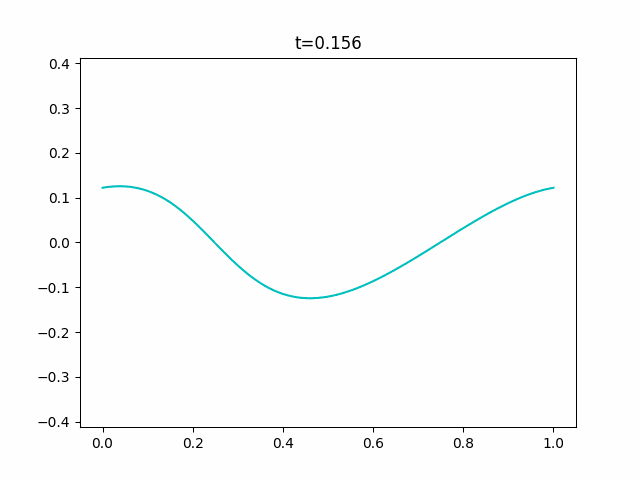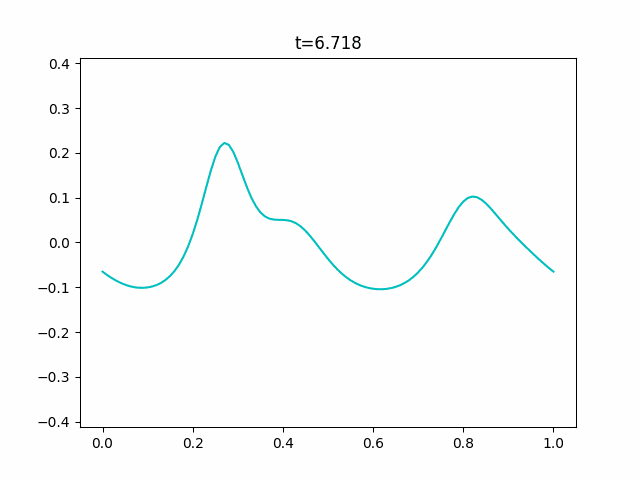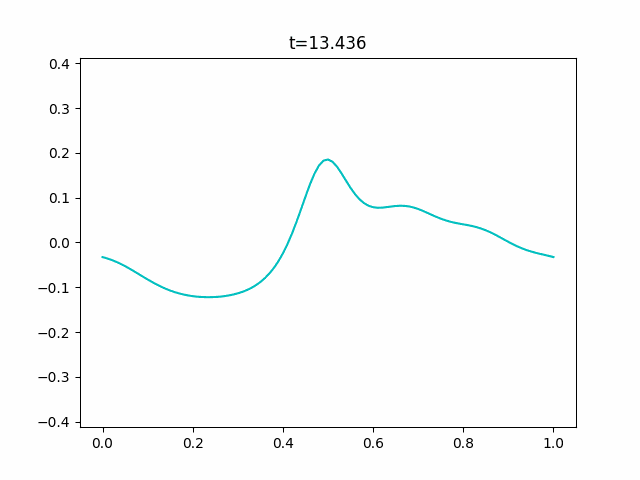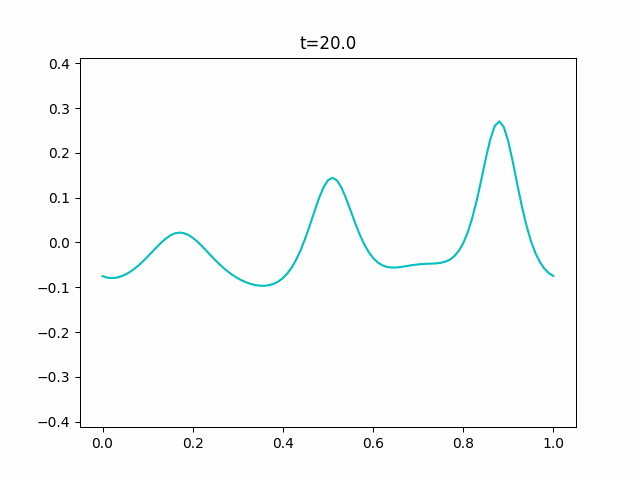
実験コード
import sys
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as anim
def is_float(value):
try:
float(value)
except ValueError:
return False
else:
return True
def get_params():
"""Get parameters from command prompt."""
kwds = {}
kwds["Nx"] = 100
kwds["Nt"] = 10000
kwds["x_range"] = 1.0
kwds["y_range"] = 0.125
kwds["t_range"] = 20.0
kwds["delta"] = 0.01
kwds["frames"] = 128
kwds["interval"] = 100
kwds["title"] = "KdV"
kwds["fps"] = 10
opts = sys.argv[1:]
for opt in opts:
key, value = opt.split("=")
if value.isdecimal():
value = int(value)
elif is_float(value):
value = float(value)
kwds[key] = value
return kwds
def _cal_next(i, y, t, n, Nx, ratio1, ratio2, y_max):
f = np.zeros(Nx+1)
for j in range(Nx+1):
p2 = y[n, (j+2)%Nx]
p1 = y[n, (j+1)%Nx]
m1 = y[n, (j-1)%Nx]
m2 = y[n, (j-2)%Nx]
numerator1 = (p1 + y[n, j] + m1)*(p1 - m1)
numerator2 = (p2 - 2*p1 + 2*m1 - m2)
f[j] = - ratio1*numerator1 - ratio2*numerator2
if i == 0:
y[n+1] += 0.5*f
else:
y[n+1] = y[n-1] + f
y[n-1] = y[n].copy()
y[n] = y[n+1].copy()
if np.max(y[n+1]) > 1.1*y_max or np.min(y[n+1]) < -1.1*y_max:
print("Overflow will occur.")
print("t = {}".format(t[i]))
sys.exit(1)
if np.any(np.isnan(y[n+1])):
print("Not a number has come.")
print("t = {}".format(t[i]))
sys.exit(1)
return y
def init(x, y_range, n):
return y_range*np.tile(np.cos(2*np.pi*x), (n+2, 1))
def update(i, frames, y, x, t, n, Nx, Nt, ratio1, ratio2, dt, y_max):
for j in range(int(i/frames*Nt), int((i+1)/frames*Nt)):
per = int((j+1)/Nt*50)
bar = "/"*per + " "*(50 - per)
print("\r[{}]".format(bar), end="")
y = _cal_next(j, y, t, n, Nx, ratio1, ratio2, y_max)
plt.cla()
plt.ylim(-1.1*y_max, 1.1*y_max)
plt.plot(x, y[n], "c")
plt.title("t={}".format(np.round(t[int((i+1)/frames*Nt)], 3)))
def wave_plot(x_range=0.0, t_range=0.0, y_range=0.0, Nx=0, Nt=0,
delta=0.0, frames=0, interval=0, title="", fps=0):
n = 1
x = np.linspace(0.0, x_range, Nx+1)
t = np.linspace(0.0, t_range, Nt+1)
y = init(x, y_range, n)
y_max = np.max(y)*3
dx = x[1] - x[0]
dt = t[1] - t[0]
ratio1 = dt/(3.0*dx)
ratio2 = dt*delta**2/dx**3
print("check values")
print("\t dx = {},\t dt = {}".format(dx, dt))
print("\tratio1 = {},\tratio2 = {}".format(ratio1, ratio2))
args = (frames, y, x, t, n, Nx, Nt, ratio1, ratio2, dt, y_max)
fig = plt.figure()
ani = anim.FuncAnimation(fig, update, fargs=args,
frames=frames, interval=interval)
ani.save(title+".gif", writer="pillow", fps=fps)
if __name__ == "__main__":
kwds = get_params()
wave_plot(**kwds)
$ python burgers.py (オプション)
| オプション | 説明 |
|---|---|
| Nx | x軸方向の分割数 |
| Nt | 時間方向の分割数 |
| x_range | x軸方向の長さ |
| y_range | y軸方向の範囲 |
| t_range | 時間方向の長さ |
| delta | 無次元化係数 |
| frames | GIFの枚数 |
| interval | GIFの間隔 |
| title | GIFのタイトル |
| fps | GIFのFPS |
y^{(0)} = \cfrac{c}{2} \textrm{sech}^2 \cfrac{3}{4} \sqrt{\cfrac{c}{\delta}} (x - \theta_0)
y_t + 6 y y_x + y_{xxx} = 0
y^{(t)} = \cfrac{c}{2} \textrm{sech}^2 \cfrac{\sqrt{c}}{2} (x - ct - \theta_0)
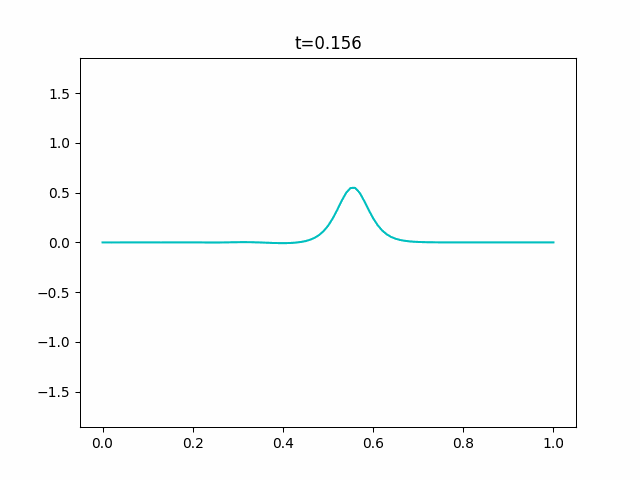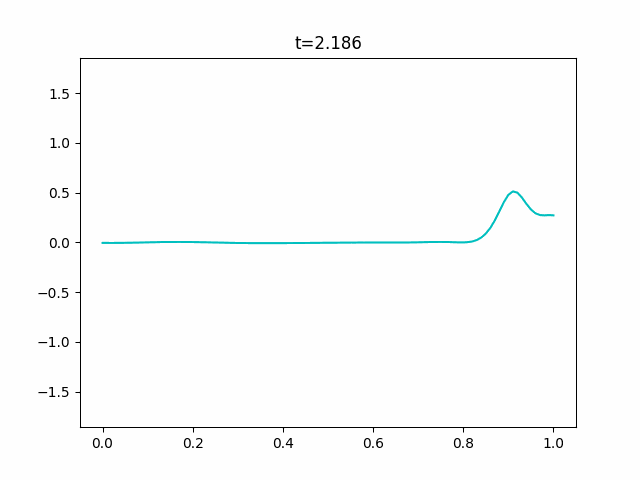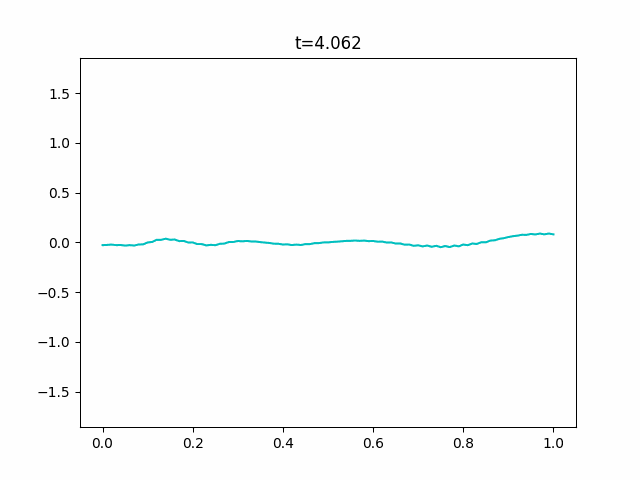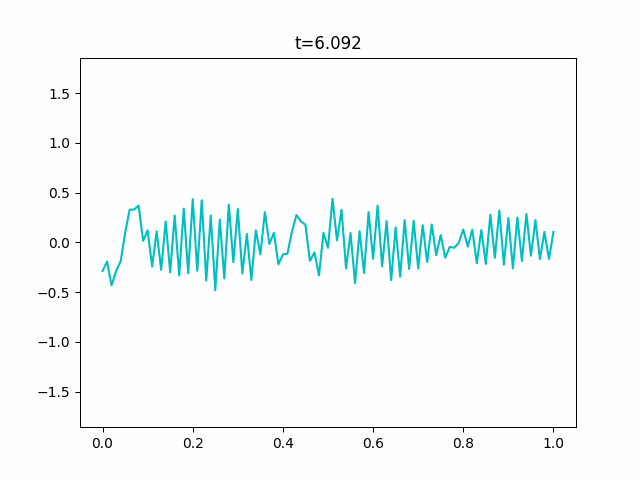
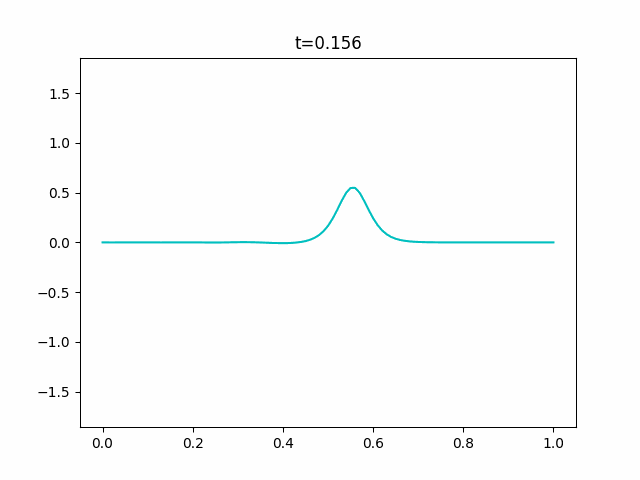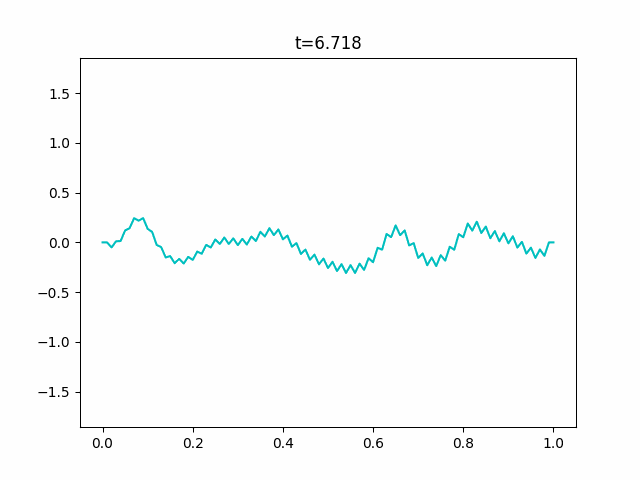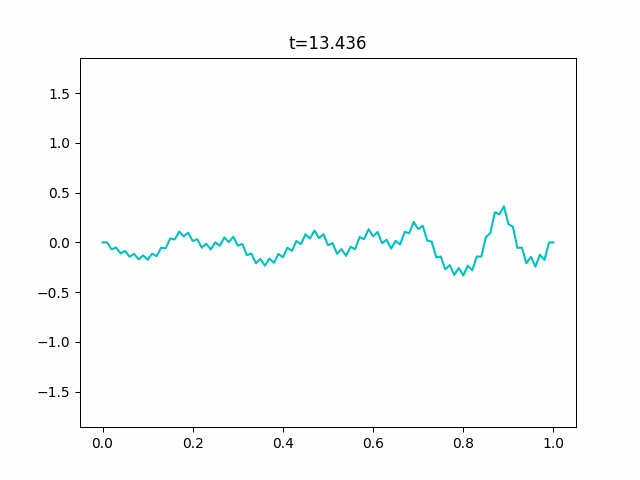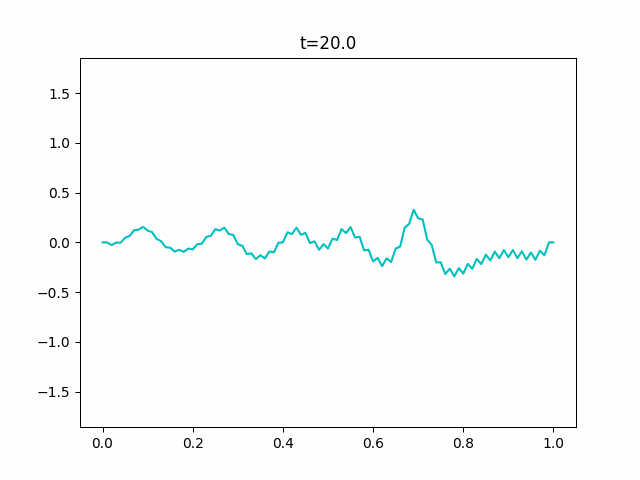
KdV方程式で描けない反射をシミュレーションする
※先に言っておきます。この数値計算はうまくいきませんでした。
KdV方程式は周期境界条件でないとうまく数値計算することができません。
自由端
import sys
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as anim
def is_float(value):
try:
float(value)
except ValueError:
return False
else:
return True
def get_params():
"""Get parameters from command prompt."""
kwds = {}
kwds["Nx"] = 100
kwds["Nt"] = 10000
kwds["x_range"] = 1.0
kwds["y_range"] = 0.125
kwds["t_range"] = 20.0
kwds["delta"] = 0.01
kwds["frames"] = 128
kwds["interval"] = 100
kwds["title"] = "KdV_free"
kwds["fps"] = 10
opts = sys.argv[1:]
for opt in opts:
key, value = opt.split("=")
if value.isdecimal():
value = int(value)
elif is_float(value):
value = float(value)
kwds[key] = value
return kwds
def _cal_next(i, y, t, n, Nx, ratio1, ratio2, delta, dt, dx, y_max):
f = np.zeros(Nx-3)
for j in range(2, Nx-1):
p2 = y[n, j + 2]
p1 = y[n, j + 1]
m1 = y[n, j - 1]
m2 = y[n, j - 2]
numerator1 = (p1 + y[n, j] + m1)*(p1 - m1)
numerator2 = (p2 - 2*p1 + 2*m1 - m2)
f[j-2] = - ratio1*numerator1 - ratio2*numerator2
if i == 0:
y[n+1, 2:Nx-1] += 0.5*f
else:
y[n+1, 2:Nx-1] = y[n-1, 2:Nx-1] + f
y[n+1, 0:2] = y[n+1, 3:5]
y[n+1, Nx-1:Nx+1] = y[n+1, Nx-3:Nx-1]
y[n-1] = y[n].copy()
y[n] = y[n+1].copy()
if np.max(y[n+1]) > 1.1*y_max or np.min(y[n+1]) < -1.1*y_max:
print("Overflow will occur.")
print("t = {}".format(t[i]))
sys.exit(1)
if np.any(np.isnan(y[n+1])):
print("Not a number has come.")
print("t = {}".format(t[i]))
sys.exit(1)
return y
def init(x, y_range, n, delta):
#return np.tile(y_range*np.cos(2*np.pi*x), (n+2, 1))
c = 9
return np.tile(y_range*0.5*c
/np.cosh(0.75*np.sqrt(c/delta)*(x-np.mean(x)))**2, (n+2, 1))
def update(i, frames, y, x, t, n, Nx, Nt, ratio1, ratio2, delta, dt, dx, y_max):
for j in range(int(i/frames*Nt), int((i+1)/frames*Nt)):
per = int((j+1)/Nt*50)
bar = "/"*per + " "*(50 - per)
print("\r[{}]".format(bar), end="")
y = _cal_next(j, y, t, n, Nx, ratio1, ratio2, delta, dt, dx, y_max)
plt.cla()
plt.ylim(-1.1*y_max, 1.1*y_max)
plt.plot(x, y[n], "c")
plt.title("t={}".format(np.round(t[int((i+1)/frames*Nt)], 3)))
def wave_plot(x_range=0.0, t_range=0.0, y_range=0.0, Nx=0, Nt=0,
delta=0.0, frames=0, interval=0, title="", fps=0):
n = 1
x = np.linspace(0.0, x_range, Nx+1)
t = np.linspace(0.0, t_range, Nt+1)
y = init(x, y_range, n, delta)
y_max = np.max(y)*3
dx = x[1] - x[0]
dt = t[1] - t[0]
ratio1 = dt/(3.0*dx)
ratio2 = dt*delta**2/dx**3
print("check values")
print("\t dx = {},\t dt = {}".format(dx, dt))
print("\tratio1 = {},\tratio2 = {}".format(ratio1, ratio2))
args = (frames, y, x, t, n, Nx, Nt, ratio1, ratio2, delta, dt, dx, y_max)
fig = plt.figure()
ani = anim.FuncAnimation(fig, update, fargs=args,
frames=frames, interval=interval)
ani.save(title+".gif", writer="pillow", fps=fps)
if __name__ == "__main__":
kwds = get_params()
wave_plot(**kwds)
固定端
import sys
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as anim
def is_float(value):
try:
float(value)
except ValueError:
return False
else:
return True
def get_params():
"""Get parameters from command prompt."""
kwds = {}
kwds["Nx"] = 100
kwds["Nt"] = 10000
kwds["x_range"] = 1.0
kwds["y_range"] = 0.125
kwds["t_range"] = 20.0
kwds["delta"] = 0.01
kwds["frames"] = 128
kwds["interval"] = 100
kwds["title"] = "KdV_fixed"
kwds["fps"] = 10
opts = sys.argv[1:]
for opt in opts:
key, value = opt.split("=")
if value.isdecimal():
value = int(value)
elif is_float(value):
value = float(value)
kwds[key] = value
return kwds
def _cal_next(i, y, t, n, Nx, ratio1, ratio2, delta, dt, dx, y_max):
f = np.zeros(Nx-3)
for j in range(2, Nx-1):
p2 = y[n, j + 2]
p1 = y[n, j + 1]
m1 = y[n, j - 1]
m2 = y[n, j - 2]
numerator1 = (p1 + y[n, j] + m1)*(p1 - m1)
numerator2 = (p2 - 2*p1 + 2*m1 - m2)
f[j-2] = - ratio1*numerator1 - ratio2*numerator2
if i == 0:
y[n+1, 2:Nx-1] += 0.5*f
else:
y[n+1, 2:Nx-1] = y[n-1, 2:Nx-1] + f
y[n-1] = y[n].copy()
y[n] = y[n+1].copy()
if np.max(y[n+1]) > 1.1*y_max or np.min(y[n+1]) < -1.1*y_max:
print("Overflow will occur.")
print("t = {}".format(t[i]))
sys.exit(1)
if np.any(np.isnan(y[n+1])):
print("Not a number has come.")
print("t = {}".format(t[i]))
sys.exit(1)
return y
def init(x, y_range, n, delta):
#return np.tile(y_range*np.cos(2*np.pi*x), (n+2, 1))
c = 9
return np.tile(y_range*0.5*c
/np.cosh(0.75*np.sqrt(c/delta)*(x-np.mean(x)))**2, (n+2, 1))
def update(i, frames, y, x, t, n, Nx, Nt, ratio1, ratio2, delta, dt, dx, y_max):
for j in range(int(i/frames*Nt), int((i+1)/frames*Nt)):
per = int((j+1)/Nt*50)
bar = "/"*per + " "*(50 - per)
print("\r[{}]".format(bar), end="")
y = _cal_next(j, y, t, n, Nx, ratio1, ratio2, delta, dt, dx, y_max)
plt.cla()
plt.ylim(-1.1*y_max, 1.1*y_max)
plt.plot(x, y[n], "c")
plt.title("t={}".format(np.round(t[int((i+1)/frames*Nt)], 3)))
def wave_plot(x_range=0.0, t_range=0.0, y_range=0.0, Nx=0, Nt=0,
delta=0.0, frames=0, interval=0, title="", fps=0):
n = 1
x = np.linspace(0.0, x_range, Nx+1)
t = np.linspace(0.0, t_range, Nt+1)
y = init(x, y_range, n, delta)
y_max = np.max(y)*3
dx = x[1] - x[0]
dt = t[1] - t[0]
ratio1 = dt/(3.0*dx)
ratio2 = dt*delta**2/dx**3
print("check values")
print("\t dx = {},\t dt = {}".format(dx, dt))
print("\tratio1 = {},\tratio2 = {}".format(ratio1, ratio2))
args = (frames, y, x, t, n, Nx, Nt, ratio1, ratio2, delta, dt, dx, y_max)
fig = plt.figure()
ani = anim.FuncAnimation(fig, update, fargs=args,
frames=frames, interval=interval)
ani.save(title+".gif", writer="pillow", fps=fps)
if __name__ == "__main__":
kwds = get_params()
wave_plot(**kwds)
なのでこの仮定をする前の偏微分方程式を数値解析すれば反射も実現できるはずです。
そこで、KdV方程式の一つ前のブジネスク(Boussinesq)方程式を数値解析します。
\left\{ \begin{array}[cc]
c\cfrac{\partial y}{\partial t} + h \cfrac{\partial v}{\partial x} + v \cfrac{\partial y}{\partial x} + y \cfrac{\partial v}{\partial x} &= 0 \\
\cfrac{\partial v}{\partial x} + g \cfrac{\partial y}{\partial x} + v \cfrac{\partial v}{\partial x} - \cfrac{h^2}{3}\cfrac{\partial^3 v}{\partial x^2 \partial t} &= 0
\end{array} \right.
\Leftrightarrow
\left\{ \begin{array}[cc]
yy_t + (h + y) v_x + v y_x &= 0 \\
v_t + g y_x + v v_x - \cfrac{h^2}{3} v_{xxt} &= 0
\end{array} \right.
$y$は変位、$v$は流速、$h$は水深、$g$は重力加速度になります。この連立偏微分方程式をうまく差分方程式にして解きます。
なお、以下に書く差分方程式化と数値解析の過程はどうやって導いたかは覚えていません...確か何かの論文を参考にしたはず...
先に述べておきますが、変位$y$については自由端、流速$v$については固定端で差分化します。
- $y_t + (h + y) v_x + v y_x = 0$を次のように差分化します。こうすると次のように変形できます。
\begin{align} y_t &= \cfrac{\hat{y}_j - y^{(n)}_j}{\Delta t} & y &= \cfrac{1}{2} \left( \hat{y}_j + y^{(n)}_j \right) \\ v_x &= \cfrac{v^{(n)}_{j+1} - v^{(n)}_{j-1}}{2 \Delta x} & y_x &= \cfrac{y^{(n)}_{j+1} - y^{(n)}_{j-1}}{2 \Delta x} \end{align}\begin{align} \hat{y}_j &= \cfrac{y^{(n)}_j - \cfrac{1}{4} \cfrac{\Delta t}{\Delta x} \left\{ \left( 2h + y^{n)}_j \right) \left( v^{(n)}_{j+1} - v^{(n)}_{j-1} \right) + 2 v^{(n)}_j \left( y^{(n)}_{j+1} - y^{(n)}_{j-1} \right) \right\}}{1 + \cfrac{1}{4} \cfrac{\Delta t}{\Delta x} \left( v^{(n)}_{j+1} - v^{(n)}_{j-1} \right)} \\ \hat{y}_0 &= \cfrac{y^{(n)}_0 - \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} \left( 2h + y^{(n)}_0 \right) v^{(n)}_1}{1 + \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} v^{(n)}_1} \qquad \hat{y}_{N_x} = \cfrac{y^{(n)}_{N_x} + \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} \left( 2h + y^{(n)}_{N_x} \right) v^{(n)}_{N_x-1}}{1 - \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} v^{(n)}_{N_x-1}} \end{align}ここで、$\hat{y}$は次時刻の仮の変位です。
2. $v_t + g y_x + v v_x - \cfrac{h^2}{3} v_{xxt} = 0$を次のように差分化します。このように差分化すると行列積でまとめることができます。\begin{align} v_t &= \cfrac{v^{(n+1)}_j - v^{(n)}_j}{\Delta t} & y_x &= \cfrac{\hat{y}_{j+1} - \hat{y}_{j-1} + y^{(n)}_{j+1} - y^{(n)}_{j-1}}{4 \Delta x}\\ v_x &= \cfrac{v^{(n+1)}_{j+1} - v^{(n+1)}_{j-1} + v^{(n)}_{j+1} - v^{(n)}_{j-1}}{4 \Delta x} & v_{xxt} &= \cfrac{v^{(n+1)}_{j+1} - 2 v^{(n+1)}_j + v^{(n+1)}_{j-1} - v^{(n)}_{j+1} + 2 v^{(n)}_j - v^{(n)}_{j-1}}{\Delta x^2 \Delta t} \end{align}この疎行列をきちんと書き下すと以下のようになります。\begin{align} \left( \begin{array}[c] -- \cfrac{1}{4} \cfrac{\Delta t}{\Delta x} v^{(n)}_j - \cfrac{h^2}{3} \cfrac{1}{\Delta x^2} \\ 1 + 2 \cfrac{h^2}{3} \cfrac{1}{\Delta x^2} \\ \cfrac{1}{4} \cfrac{\Delta t}{\Delta x} v^{(n)}_j - \cfrac{h^2}{3} \cfrac{1}{\Delta x^2} \end{array} \right)^{\top} \left( \begin{array}[c] vv^{(n+1)}_{j-1} \\ v^{(n+1)}_j \\ v^{(n+1)}_{j+1} \end{array} \right) &= v^{(n)}_j - \cfrac{1}{4} \cfrac{\Delta t}{\Delta x} \left\{ g \left( \hat{y}_{j+1} - \hat{y}_{j-1} + y^{(n)}_{j+1} - y^{(n)}_{j-1} \right) + v^{(n)}_j \left( v^{(n)}_{j+1} - v^{(n)}_{j-1} \right) \right\} - \cfrac{h^2}{3} \cfrac{1}{\Delta x^2} \left( v^{(n)}_{j+1} - 2 v^{(n)}_j + v^{(n)}_{j-1} \right) \\ \left( \begin{array}[c] 11 + 2 \cfrac{h^2}{3} \cfrac{1}{\Delta x^2} \\ \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} v^{(n)}_0 \end{array} \right)^{\top} \left( \begin{array}[c] vv^{(n+1)}_0 \\ v^{(n+1)}_1 \end{array} \right) &= v^{(n)}_0 - \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} v^{(n)}_0 v^{(n)}_1 + 2 \cfrac{h^2}{3} \cfrac{1}{\Delta x^2} v^{(n)}_0 \qquad \left( \begin{array}[c] -- \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} v^{(n)}_{N_x} \\ 1 + 2 \cfrac{h^2}{3} \cfrac{1}{\Delta x^2} \end{array} \right)^{\top} \left( \begin{array}[c] vv^{(n+1)}_{N_x-1} \\ v^{(n+1)}_{N_x} \end{array} \right) = v^{(n)}_{N_x} + \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} v^{(n)}_{N_x} v^{(n)}_{N_x-1} + 2 \cfrac{h^2}{3} \cfrac{1}{\Delta x^2} v^{(n)}_{N_x} \end{align}3. 最後にもう一度$y_t + (h + y) v_x + v y_x = 0$を次のように差分化します。\begin{array}[ccc] pp_j = - \cfrac{1}{4} \cfrac{\Delta t}{\Delta x} v^{(n)}_j - \cfrac{h^2}{3} \cfrac{1}{\Delta x^2}, & q = 1 + 2 \cfrac{h^2}{3} \cfrac{1}{\Delta x^2}, & r_j = \cfrac{1}{4} \cfrac{\Delta t}{\Delta x} v^{(n)}_j - \cfrac{h^2}{3} \cfrac{1}{\Delta x^2} \end{array} \\ s_j = v^{(n)}_j - \cfrac{1}{4} \cfrac{\Delta t}{\Delta x} \left\{ g \left( \hat{y}_{j+1} - \hat{y}_{j-1} + y^{(n)}_{j+1} - y^{(n)}_{j-1} \right) + v^{(n)}_j \left( v^{(n)}_{j+1} - v^{(n)}_{j-1} \right) \right\} - \cfrac{h^2}{3} \cfrac{1}{\Delta x^2} \left( v^{(n)}_{j+1} - 2 v^{(n)}_j + v^{(n)}_{j-1} \right) \\ \left( \begin{array}[ccccccccccc] qq & \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} v^{(n)}_0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 \\ p_1 & q & r_1 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 \\ 0 & p_2 & q & r_2 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & p_3 & q & r_3 & \cdots & 0 & 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & 0 & \cdots & p_{N_x-3} & q & r_{N_x-3} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \cdots & 0 & p_{N_x-2} & q & r_{N_x-2} & 0 \\ 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & p_{N_x-1} & q & r_{N_x-1} \\ 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & - \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} v^{(n)}_{N_x} & q \end{array} \right) \left( \begin{array}[c] vv^{(n+1)}_0 \\ v^{(n+1)}_1 \\ v^{(n+1)}_2 \\ v^{(n+1)}_3 \\ \vdots \\ \vdots \\ \vdots \\ v^{(n+1)}_{N_x-3} \\ v^{(n+1)}_{N_x-2} \\ v^{(n+1)}_{N_x-1} \\ v^{(n+1)}_{N_x} \end{array} \right) = \left( \begin{array}[c] vv^{(n)}_0 - \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} v^{(n)}_0 v^{(n)}_1 + 2 \cfrac{h^2}{3} \cfrac{1}{\Delta x^2} v^{(n)}_0 \\ s_1 \\ s_2 \\ s_3 \\ \vdots \\ \vdots \\ \vdots \\ s_{N_x-3} \\ s_{N_x-2} \\ s_{N_x-1} \\ v^{(n)}_{N_x} + \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} v^{(n)}_{N_x} v^{(n)}_{N_x-1} + 2 \cfrac{h^2}{3} \cfrac{1}{\Delta x^2} v^{(n)}_{N_x} \end{array} \right)こうすると次のように変形できます。\begin{align} y_t &= \cfrac{y^{(n+1)}_j - y^{(n)}_j}{\Delta t} & v_x &= \cfrac{1}{4 \Delta x} \left( v^{(n+1)}_{j+1} - v^{(n+1)}_{j-1} + v^{(n)}_{j+1} - v^{(n)}_{j-1} \right) \\ v &= \cfrac{1}{2} \left( v^{(n+1)}_j + v^{(n)}_j \right) & y_x &= \cfrac{y^{(n)}_{j+1} - y^{(n)}_{j-1}}{2 \Delta x} \end{align}\begin{align} y^{(n+1)}_j &= y^{(n)}_j - \cfrac{1}{4} \cfrac{\Delta t}{\Delta x} \left\{ \left( h + y^{(n)}_j \right) \left( v^{(n+1)}_{j+1} - v^{(n+1)}_{j-1} + v^{(n)}_{j+1} - v^{(n)}_{j-1} \right) + \left( v^{(n+1)}_j + v^{(n)}_j \right) \left( y^{(n)}_{j+1} - y^{(n)}_{j-1} \right) \right\} \\ y^{(n+1)}_0 &= y^{(n)}_0 - \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} \left( h + y^{(n)}_0 \right) \left( v^{(n+1)}_1 + v^{(n)}_1 \right) \qquad y^{(n+1)}_{N_x} = y^{(n)}_{N_x} + \cfrac{1}{2} \cfrac{\Delta t}{\Delta x} \left( h + y^{(n)}_{N_x} \right) \left( v^{(n+1)}_{N_x} + v^{(n)}_{N_x} \right) \end{align}実験コード
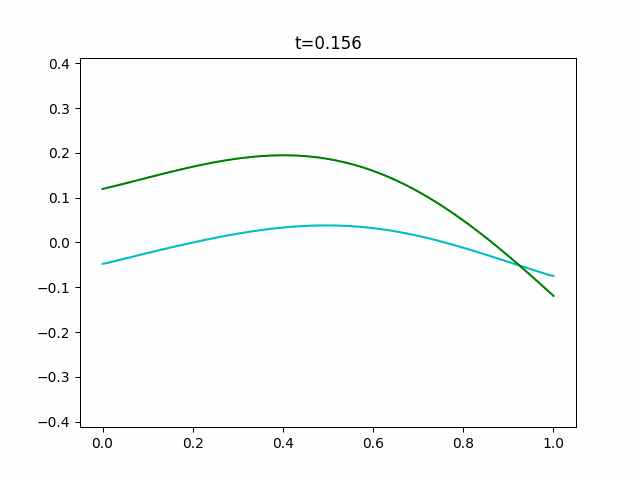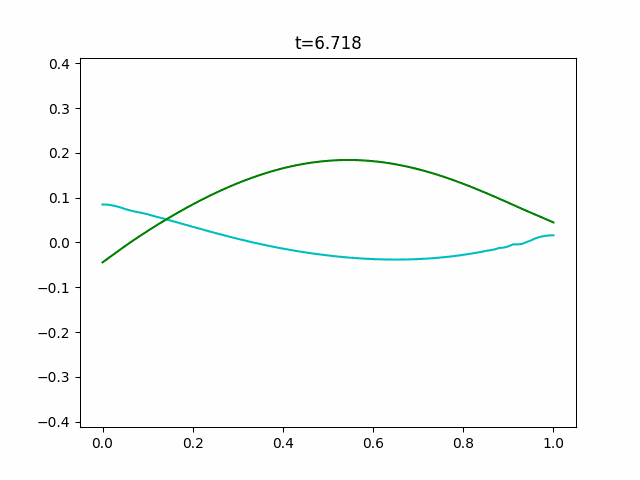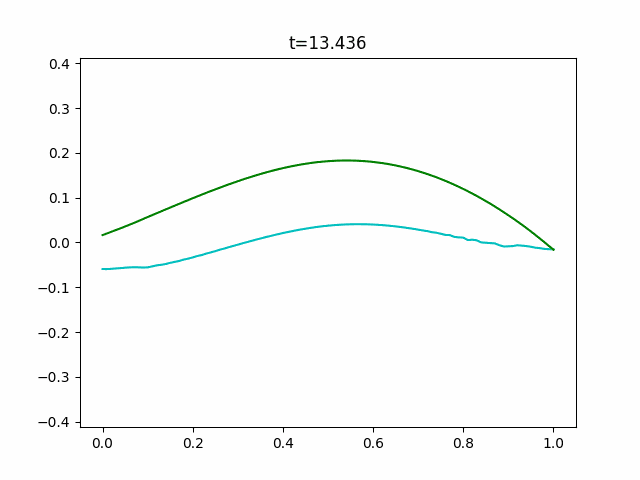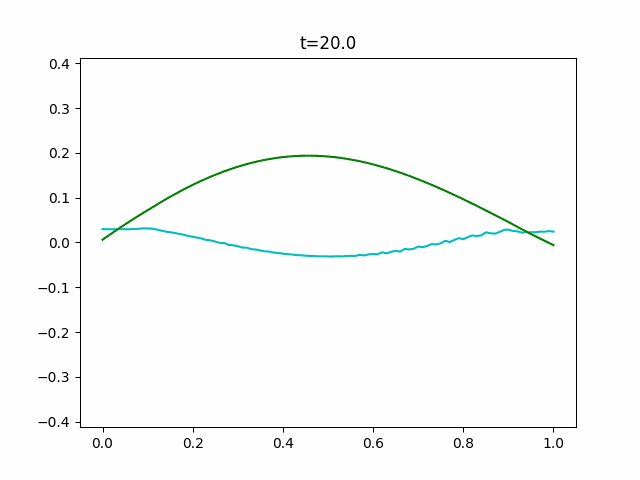
Boussinesq.pyimport sys import numpy as np import scipy.sparse as sp from scipy.sparse.linalg import dsolve import matplotlib.pyplot as plt import matplotlib.animation as anim def is_float(value): try: float(value) except ValueError: return False else: return True def get_params(): """Get parameters from command prompt.""" kwds = {} kwds["Nx"] = 100 kwds["Nt"] = 10000 kwds["x_range"] = 1.0 kwds["y_range"] = 0.125 kwds["t_range"] = 20.0 kwds["h"] = 1.0 kwds["g"] = 9.8 kwds["frames"] = 128 kwds["interval"] = 100 kwds["title"] = "Boussinesq" kwds["fps"] = 10 opts = sys.argv[1:] for opt in opts: key, value = opt.split("=") if value.isdecimal(): value = int(value) elif is_float(value): value = float(value) kwds[key] = value return kwds def _cal_next(i, y, v, t, n, Nx, ratio1, ratio2, h, g, dt, dx, y_max): tilde_y = np.zeros(Nx+1) tilde_y[0] = ((y[n, 0] - 2*ratio1*(2*h + y[n, 0])*v[n, 1]) /(1 + 2*ratio1*v[n, 1])) tilde_y[Nx] = ((y[n, Nx] + 2*ratio1*(2*h + y[n, Nx])*v[n, Nx-1]) /(1 - 2*ratio1*v[n, Nx-1])) for j in range(1, Nx): tilde_y[j] = ((y[n, j] - ratio1*((2*h + y[n, j])*(v[n, j+1] - v[n, j-1]) + 2*v[n, j]*(y[n, j+1] - y[n, j-1]))) /(1 + ratio1*(v[n, j+1] - v[n, j-1]))) inv_coef = sp.lil_matrix((Nx+1, Nx+1)) ans = np.zeros(Nx+1) q = 1 + 2*ratio2 inv_coef[0, 0] = q inv_coef[0, 1] = 2*ratio1*v[n, 0] inv_coef[Nx, Nx-1] = -2*ratio1*v[n, Nx] inv_coef[Nx, Nx] = q ans[0] = v[n, 0] - 2*ratio1*v[n, 0]*v[n, 1] - 2*ratio2*v[n, 0] ans[Nx] = v[n, Nx] + 2*ratio1*v[n, Nx-1]*v[n, Nx] - 2*ratio2*v[n, Nx] for j in range(1, Nx): inv_coef[j, j-1] = -ratio1*v[n, j] - ratio2 inv_coef[j, j] = q inv_coef[j, j+1] = ratio1*v[n, j] - ratio2 ans[j] = (v[n, j] - ratio1*(g*(tilde_y[j+1] - tilde_y[j-1] + y[n, j+1] - y[n, j-1]) + v[n, j]*(v[n, j+1] - v[n, j-1])) - ratio2*(v[n, j+1] - 2*v[n, j] + v[n, j-1])) inv_coef = inv_coef.tocsr() v[n+1] = dsolve.spsolve(inv_coef, ans) y[n+1, 0] = y[n, 0] - 2*ratio1*(h + y[n, 0])*(v[n+1, 1] + v[n, 1]) y[n+1, Nx] = y[n, Nx] + 2*ratio1*(h + y[n, Nx])*(v[n+1, Nx-1] + v[n, Nx-1]) for j in range(1, Nx): y[n+1, j] = y[n, j] - ratio1*((h + y[n, j])*(v[n+1, j+1] - v[n+1, j-1] + v[n, j+1] - v[n, j-1]) + (v[n+1, j] + v[n, j]) * (y[n, j+1] - y[n, j-1])) y[n] = y[n+1].copy() v[n] = v[n+1].copy() if np.max(y[n+1]) > 1.1*y_max or np.min(y[n+1]) < -1.1*y_max: print("Overflow will occur.") print("t = {}".format(t[i])) sys.exit(1) if np.any(np.isnan(y[n+1])): print("Not a number has come.") print("t = {}".format(t[i])) sys.exit(1) if np.max(v[n+1]) > 1.1*y_max or np.min(v[n+1]) < -1.1*y_max: print("Overflow will occur.") print("t = {}".format(t[i])) sys.exit(1) if np.any(np.isnan(v[n+1])): print("Not a number has come.") print("t = {}".format(t[i])) sys.exit(1) return y, v def init(x, y_range, n, h, g): y = np.tile(y_range*np.cos(np.pi*x/np.max(x)), (n+2, 1)) #c = 9 #y = np.tile(y_range*0.5*c/np.cosh(0.5*np.sqrt(c)*(x-np.mean(x)))**2, # (n+2, 1)) v = y.copy() return y, v def update(i, frames, y, v, x, t, n, Nx, Nt, ratio1, ratio2, h, g, dt, dx, y_max): for j in range(int(i/frames*Nt), int((i+1)/frames*Nt)): per = int((j+1)/Nt*50) bar = "/"*per + " "*(50 - per) print("\r[{}]".format(bar), end="") y, v = _cal_next(j, y, v, t, n, Nx, ratio1, ratio2, h, g, dt, dx, y_max) plt.cla() plt.ylim(-1.1*y_max, 1.1*y_max) plt.plot(x, y[n], "c") plt.plot(x, v[n], "g") plt.title("t={}".format(np.round(t[int((i+1)/frames*Nt)], 3))) def wave_plot(x_range=0.0, t_range=0.0, y_range=0.0, Nx=0, Nt=0, h=0.0, g=0.0, frames=0, interval=0, title="", fps=0): n = 0 x = np.linspace(0.0, x_range, Nx+1) t = np.linspace(0.0, t_range, Nt+1) y, v = init(x, y_range, n, h, g) y_max = np.max(y)*3 dx = x[1] - x[0] dt = t[1] - t[0] ratio1 = 0.25*dt/dx ratio2 = h**2 / dx**2 / 3 print("check values") print("\t dx = {},\t dt = {}".format(dx, dt)) print("\tratio1 = {},\tratio2 = {}".format(ratio1, ratio2)) args = (frames, y, v, x, t, n, Nx, Nt, ratio1, ratio2, h, g, dt, dx, y_max) fig = plt.figure() ani = anim.FuncAnimation(fig, update, fargs=args, frames=frames, interval=interval) ani.save(title+".gif", writer="pillow", fps=fps) if __name__ == "__main__": kwds = get_params() wave_plot(**kwds)ソリトン解がどういう数式か分からなかったのでそっちは実験できていません。また、よくよく見るとこのGIFも実はちょっとブレていることに気づくと思います。
ついでにx_rangeを変化させると計算に失敗します。
多分差分解法がまずいか、どこかコーディングミスしているか、いろいろと原因が考えられるのですがちょっと分からないので置いておきます...
何がまずいかわかる方はぜひ教えてください。おわりに
久しぶりにマクロシミュレーションっぽいことやりましたが、やっぱり目で見える成果はやりがいあっていいですね〜
今回はBoussinesq方程式に敗北してしまいましたが、またいろいろな差分解法で試して見ます。参考