ソリトン〜計算機から生まれた数理物理学〜

こんばんは。数学とコンピュータ II　Advent Calendar 10100日目の記事を書かせていただきます。

この記事では、ソリトンと呼ばれる対象についてご紹介します。

やや数学・物理色が強め、ですが、あまり詳細に囚われず読んでいただければ幸いです。
ちなみにソリトンは歴史的に見ても計算機のおかげで発展したと言っても過言ではなく、一方で近年ではセルオートマトンといった対象とも関わりがありますので、テーマ的にはあっていると思います。
そして日本が元々強い分野でありながら、あまり周知されていない気がするので、もし興味ある方(特に計算機に強い方々)が増えて、この分野が活気づけばいいな、と思って今回投稿しました。

本論に入る前に

１．まずちょっと言い訳(お詫び)です。
もともとlatexで書いていて、後でマークダウン用に変換したのですが、慣れていないためレイアウト等がかなり適当です。また数式の表示に問題が有るかもしれません。随時修正しています。

２．数学や物理がある程度得意な方向けに、『進んだ注』を加えたpdfファイルを順次公開中(2017/12/29:KdV方程式の範囲は全てアップしました)です。

３．ソースコードはpythonでjupyter notebookを随時GitHubで公開予定です。

• KdV方程式のN-ソリトン解 (2017/12/29公開)

• 箱玉系で遊ぼう (2018/1/6公開)

イントロダクション

そもそも皆さんはソリトンという言葉を聞いた事があるでしょうか？
簡単に言いますと、形状を保ったまま進行し、互いに衝突・追突しても崩れないような孤立(局在)した波の事です。すなわち波の塊でありながら安定であり、粒子的に振る舞うような物理的対象です。¹

もう少しソリトンのイメージをつけたい方は、soliton, solitary wave (追加でcollisionといった単語を付け加えると良いかもしれません)といった単語で是非動画検索をしてみてください。そんな暇ないよ、という方には、動画 Collision of KdV solitons (youtube.com)をお勧めしておきますのでご覧ください。³

このソリトンの歴史的な詳細は後に譲りますが、その発見から理論的研究が本格的に進展するまでの間、100年以上の歳月が流れています。そしてこのきっかけを作ったのが、計算機の登場でした。
そして現在においても、ソリトン研究から派生した分野において計算機は重要な役割を担っていると言えます。

さて話は唐突に変わりますが、ここで次の式を見てください。

\begin{align}
y = 2\dfrac{ e^{x-t} + 4e^{2x-8t} + 2e^{3x-9t} + \tfrac{4}{9}e^{4x-10t} + \tfrac{1}{9}e^{5x-17t} }{ (1 + e^{x-t} + e^{2x-8t} + \tfrac{1}{9}e^{3x-9t} )^2}
\end{align}

皆さんは$t$が適当な実数値の時に、この実関数の概形(横軸$x$、縦軸$y$)を描けますか？
おそらく適切なプロットツールを用いればグラフの概形を描けるでしょう。

ではこれが次のような簡単な(非線形)偏微分方程式の解である、と言ったら驚くでしょうか？

\begin{align}
\dfrac{\partial}{\partial t}y + 6y \dfrac{\partial}{\partial x}y + \dfrac{\partial^3}{\partial x^3}y = 0.
\end{align}

実はこの偏微分方程式こそがソリトンを記述する方程式(KdV方程式)なのです。

しかしこれだけだと、ある簡単な偏微分方程式の特殊な解がたまたま存在しただけじゃないか、と思う方も多いでしょう。果たして、たまたま1個見つかっただけなのでしょうか？
実はこの方程式には、驚く事に各点がそれぞれ異なる解析解に対応するような$``$無限次元の空間$"$が付随しています。⁴

前半は、この単純な偏微分方程式とその解たちのお話になります。

一方で後半では、このソリトンの概念がセルオートマトンでも姿を表すというお話をご紹介します。セルオートマトンの有名な例としては、ライフゲームがあります。聞いたこと無い方は是非一度ググってみる事をおすすめします。

特に今回取り上げる系は、高橋大輔・薩摩順吉両氏により提案された。箱玉系と呼ばれているものです。⁵

なおこの箱玉系の話は、今回ご紹介する限りにおいては前半の偏微分方程式の話とは独立ですので、前半が難しかったな、あるいは興味持てなかったな、という方でも後半を読む事ができると思います。⁶

最後に、幾つか補足pdfをつけたので少しコメントしておきます。

まずソリトンの簡単な歴史については、ソリトンの夜明けまでの簡単な歴史を参照してください。ただし最近の発展については書いていません。

またソリトンは元々物理学の様々な分野で見られる現象・概念でしたが、可積分系を通して、

• 代数曲線論(楕円積分(Abel-Jacobi写像)、$\Theta$関数、Novikov予想(最後のはよく知りません))
• Kac-Moody環(佐藤-Wilson理論、頂点作用素、Drinfeld-Sokolov系)
• 量子群の表現論(クリスタル・R行列)
• 組み合わせ論(KKR対応)
• 数論(Riemann予想、特にChebyshef関数の漸近評価)
• 確率解析
• $``$離散幾何$"$(例えばtropical幾何)

といった数学の諸分野とも関係しています。⁷

KdV方程式

まず前半ではKdV方程式と呼ばれる偏微分方程式のお話をします。
一般に偏微分方程式が与えられると、原理的には数値計算でこれを解く事ができますが、今回はそういった話はしません。勿論それ自体重要な話ではありますが、それ以上に面白い数理現象が存在するからです。⁸

KdV方程式とその進行波解

まずは、(ソリトンの発見者である)Russelの追体験、というわけにはいきませんが、次のような空間方向$1$次元に広がる水面上の波を想像してください。

この波のダイナミクスを特徴づける方程式について考えていきます。

上図のように、ある時刻$t$、ある位置$x$における波の高さを$u = u(x,t)$とおきます。⁹

\begin{align}
u_t + 6uu_x + u_{xxx} = 0
\end{align}

\begin{align}
u_t := \dfrac{\partial u}{\partial t} \qquad
u_x := \dfrac{\partial u}{\partial x} \qquad
u_{xxx} := \dfrac{\partial^3 u}{\partial x^3}
\end{align}

以下、同様の記号を随時用いますが、一般化は明らかでしょう。

さて微分方程式を解く際には、一般に、適当な境界条件を定める必要があります。
ここでは境界条件として、各時刻$t$に対して$\displaystyle \lim_{x \to \pm \infty} u(x,t) = 0$を課す事にします。¹¹

準備が整いましたので、このKdV方程式を早速解いてみましょう。ただし解の形として、1個の実変数$\xi:= x-vt$ (ただし$v$は正の定数)の関数$f$でかける、すなわち
$u = f(\xi)$を仮定します。言い換えると$v f_x = f_t$との連立微分方程式を考える事に対応します。
するとこの偏微分方程式は次のような常微分方程式に帰着します：

\begin{align}
-v f_\xi(\xi) + 6 f(\xi) f_\xi(\xi) + f_{\xi\xi\xi}(\xi) = 0.
\end{align}

まず各項を$\xi$について積分してみると、

\begin{align}
-vf(\xi) + 3f(\xi)^2 + f_{\xi\xi}(\xi) = 0.
\end{align}

ここで境界条件$f,f_{\xi\xi} \rightarrow 0$ ($\xi \rightarrow \pm \infty$)を用いました。
さらに今度は$f_\xi(\xi) = \tfrac{d}{d \xi} f(\xi)$をかけて$\xi$についてまた積分すると、再び境界条件の下

\begin{align}
-\tfrac{v}{2}f(\xi)^2 + f(\xi)^3 + \tfrac{1}{2} f_\xi(\xi)^2 = 0
\end{align}

を得ます。そして変数変換

\begin{align}
\eta:=\dfrac{\sqrt{v}}{2}\xi \qquad z(\eta) := \sqrt{ \dfrac{v}{2f(\xi)} }
\end{align}

を行うとこの微分方程式は解く事ができ、

\begin{align}
\eta = \pm \int^z \dfrac{dz'}{\sqrt{z'^2 - 1}} = \cosh^{-1}(z) + \mathrm{const.}
\end{align}

となります。最後に、元の$x,t,u$で書き直すと、$u(x,t) = \dfrac{v}{2\cosh\left(\tfrac{\sqrt{v}}{2}(x-vt)-\theta\right)^2}$という解が得られます。余力がある方はこれを元のKdV方程式に代入して、実際に解になっている事を再確認してみてください。

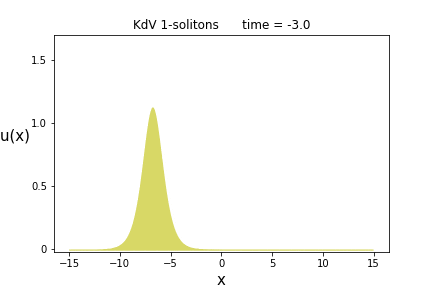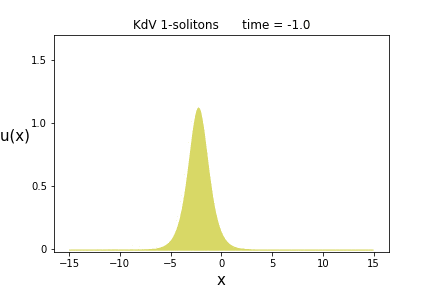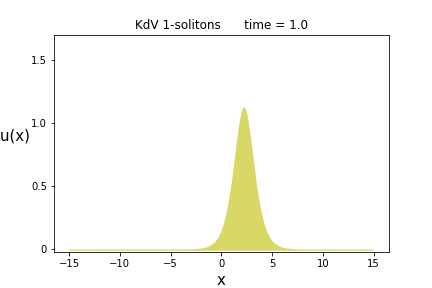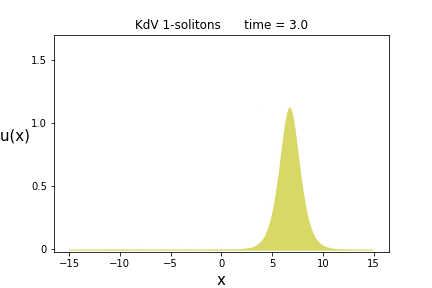
今得られた解を1-ソリトン解(または進行波解とも言う)と呼びますが、次にこの意味について説明します。
そのためにこの関数の概形を各時刻$t$で描いてみましょう。それが次のアニメーションになります。

一つの山からなる波が、時間の経過と共に右側へ進行している様子が見て取れます。
そして(この山の頂点から見た)波の形は全く変わっていない事が分かると思います。
これがまさにKdV方程式におけるソリトンなのです。

進んだ注：KdV方程式と楕円積分・Riemann面

進んだ注：KdV方程式と楕円積分・Riemann面

$\tau$関数による新たな解の考察

前節でKdV方程式の解を求めましたが、解はこれで全てでしょうか？実はこれで全てではありません。ソリトン１個を表す1-ソリトン解を求めたので、ソリトン2個を表す解も存在しそうです。

ところで線形微分方程式においては２つの解の、任意の線型結合も微分方程式の解になる事を思い出してみます。これは数学的に述べますと、線形微分方程式の解空間(線形微分演算子の核)は加法について閉じた線形空間になっていると表現できます。
一方でKdV方程式は非線形方程式ですので、２つの解の和は必ずしも解になるとは言えません。
物理学の言葉では重ね合わせの原理が成り立ないとも言えます。
しかしながら２つのソリトンの山の位置が十分離れている時は、KdV方程式の良い近似解になっていると期待できます。

以上を踏まえて、かなり天下り的ではありますが、1-ソリトン解を次のように書き換えます。

\begin{align}
u(x,t;p=\sqrt{v},\theta) = 2 \dfrac{\partial^2}{\partial x^2} \log( \cosh(\tfrac{\sqrt{v}}{2}(x-vt)-\theta )
= 2 \dfrac{\partial^2}{\partial x^2} \log( 1 + a \exp( \sqrt{v} (x-vt) ).
\end{align}

ただし$a=a(\theta):=e^{-\theta}$とおきました。
また任意の$\alpha \in \mathbb{R}$に対して、$\dfrac{\partial^2}{\partial x^2} \log(e^{\alpha x}) = 0$という事実を用いました。

ここで上記の書き換えで$\log$が表れている事に注目してください。これにより解の和は、$\log$の中では積になります。すなわち

\begin{align}
\nonumber & u(x,t;p_1,\theta_1) + u(x,t;p_2,\theta_2) \\
& \qquad\quad = 2 \dfrac{\partial^2}{\partial x^2}\log\left( 1 + a(\theta_1) \exp( p_1 (x-p_1^2t) ) \right)\left( 1 + a(\theta_2) \exp( p_2 (x-p_2^2t) ) \right)
\end{align}

であり、$\log$の中身を展開すると

\begin{align}
1 + a(\theta_1) \exp( p_1 (x-p_1^2t) ) + a(\theta_2) \exp( p_2 (x-p_2^2t) ) + a(\theta_1)a(\theta_2) \exp( (p_1+p_2)x - (p_1^3+p_2^3)t )
\end{align}

となります。勿論この1-ソリトン解の和は解になりませんが、ここで$\log$の中身第４項について、$a(\theta_1)a(\theta_2)$を$a(\theta_1)a(\theta_2)c$に置き換え、KdV方程式に代入してみます。
詳細な計算は省きますが、KdV方程式の解になる時、$c = \left( \tfrac{p_1-p_2}{p_1+p_2} \right)^2$が導かれます。ここで$x$や$t$に依らない事に注意してください。

以後、この$\log$の中身を$\tau^{(2)}(x,t)$とおくと、

\begin{align}
\nonumber \tau^{(2)}(x,t) &= 1 + \exp( p_1 x-p_1^3 t-\theta_1) + \exp( p_2 x-p_2^3 t-\theta_2) \\
&+ \left( \tfrac{p_1-p_2}{p_1+p_2} \right)^2 \exp\left( (p_1+p_2)x -(p_1^3+p_2^3)t-\theta_1-\theta_2 \right)
\end{align}

となります。

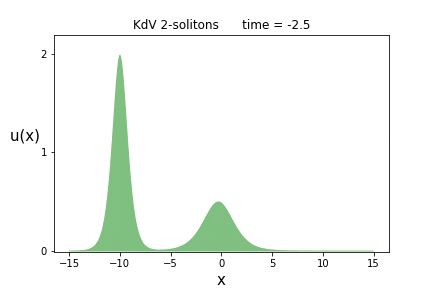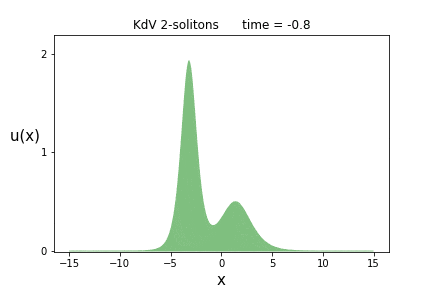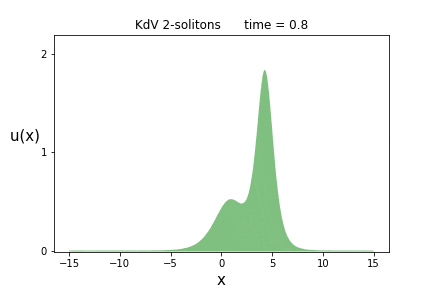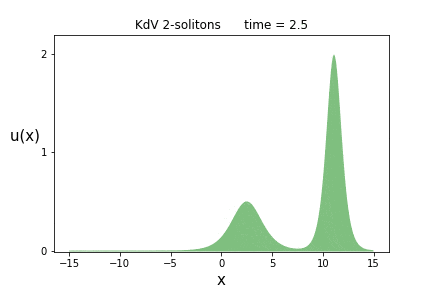
さて、この式で$p_1=1, p_2=2$とおいて$u(x,t)$を計算してみますと、実はイントロダクションで唐突に出した式に一致します。
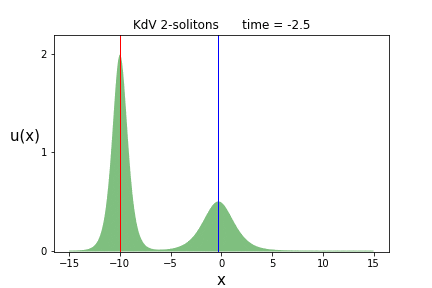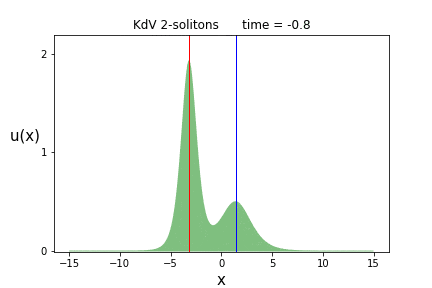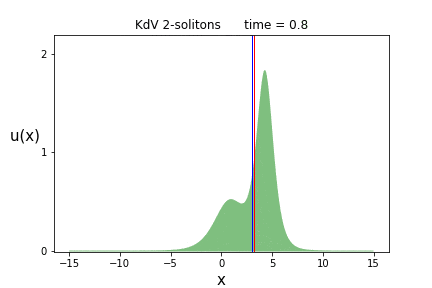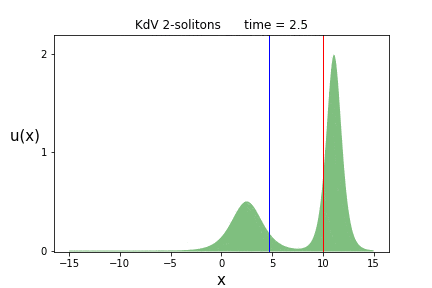
これを各時刻$t$でプロットしたものが次のアニメーションです。

背の高いソリトン(波の塊)が、背の低いソリトンを追いかけ、$t=0$付近で追いついたと思ったら、そのまま追い抜かしてしまう事が見て取れます。
これはソリトンが２つあるので、2-ソリトン解と呼ばれます。

我が道を征くソリトン達、その生き征き様には憧れてしまいますね。

$n$-ソリトン解

$2$-ソリトン解があるのだから、一般に$n$-ソリトン解があるはずだ、という期待は人としてもソリトンとしても自然なものでしょう。実際にそのような解析解はなんと存在します。
先の方法を一般化すれば原理的には解を求める事ができるのですが、$n\ge 4$以上であまりその方法は賢明でないため、ここでは結果を天下り的に与える事にします。意欲的な方はまず$\tau$関数が

\begin{align}
\tau_{xt}\tau - \tau_{x}\tau_{t} + 3\tau_{xx}^2 -4 \tau_{x}\tau_{xxx} + \tau\tau_{xxxx} = 0
\end{align}

を満たすならば、$u(x,t):=2(\log(\tau(x,t)))_{xx}$はKdV方程式を満たす事を証明し、
そして$n=3$の場合に、前節と同様の方法で3-ソリトン解を自力で求めてみてください。¹²

では、先に与えた$\tau^{(2)}(x,t)$を一般化します。$n$を1以上の整数としましょう。この時、$i \in \{1,2,\ldots,n\}$に対し、

\begin{align}
\eta_i(x,t;p_i,\theta_i) := p_i x - p_i^{\;3} t - \theta_i
\end{align}

とおき、$\tau$関数を

\begin{align}
\tau^{(n)}(x,t) := \tau(x,t;\{p\},\{\theta\}) &:= \sum_{\mu \in \{0,1\}^n} \exp\left[ \sum_{i=1}^{n} \mu_i \eta_i + \sum_{1\le i<j\le n} \mu_i \mu_j \log\left(\dfrac{p_i-p_j}{p_i+p_j} \right)^2 \right] \\
& = \sum_{I\subset \{1,2,\ldots,n\}} \prod_{\substack{i<j \\ i,j \in I}} \left(\tfrac{p_i-p_j}{p_i+p_j} \right)^2 \prod_{i \in I} e^{\eta_i(x,t)}
\end{align}

と定めましょう。ここで第１行目は$\mu = \{\mu_1\mu_2 \ldots \mu_n\}$は可能な$n$ビット列に関する和、すなわち$2^n$個の和による表現、第２行目は$1$から$n$までの整数からなる集合の冪集合に関する和による表示です。すると

\begin{align}
u^{(n)}(x,t:\{p\},\{\theta\}) := 2 \dfrac{\partial^2}{\partial x^2} \log(\tau^{(n)}(x,t;\{p\},\{\theta\}))
=
2 \left[
\dfrac{\tau^{(n)}_{xx}}{\tau^{(n)}}
-\left(
\dfrac{\tau^{(n)}_{x}}{\tau^{(n)}}
\right)^2
\right]
\end{align}

はなんとKdV方程式の解であり、これは$n$-ソリトン解と呼ばれます。これらの動く様(アニメーション)は後のお楽しみとしてとっておきましょう。

KdV方程式である事の数値的確認

さて$n$-ソリトン解の啓示を受けたわけですが、これが実際にKdV方程式の解になっている事を確認するのはとてもとても大変です。
具体的に示す方法としては、逆散乱法による方法(『進んだ注：Miura変換を経て散乱問題へ』参照)、広田形式とWronskian表示(『余談：$\tau$関数の様々な表示』参照)による方法、頂点演算子(『進んだ注：ソリトン解に潜む対称性』参照)と双線形恒等式(広田形式の別表現)による方法など幾つかあります。興味がある方は調べてみてください。

代わりにここでは、先に与えた$\tau$関数の表式を元に$u(x,t)$を計算し、それが実際にKdV方程式を満たしている事を数値的に確認する事にします。

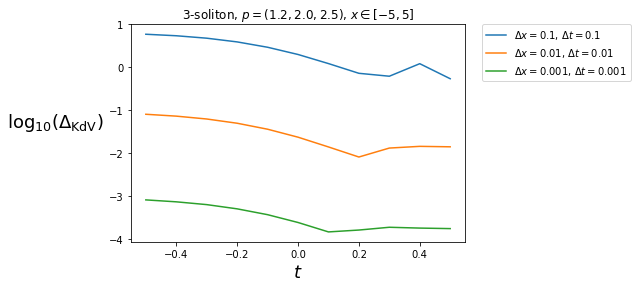
今回は$n=3$、すなわち3-ソリトン解で、$(p_1,p_2,p_3) = (1.2, 2.0, 2.5)$の場合でチェックしてみます。
なおこの数値を選んだ理由は、特にありません。

\begin{align}
K_{\mathrm{KdV}}[u](x,t) := u_t + 6uu_x + u_xxx
\end{align}

と定義すると、$u=u(x,t)$がKdV方程式の解である時、定義より$K[u](x,t) \equiv 0$を満たします。

よって、

\begin{align}
\Delta_{\mathrm{KdV}}[u](t) := \sup_{x \in \mathbb{R}} ( K[u](x,t) )
\end{align}

とおき、これが数値的に十分小さい事を確認すれば良さそうです。¹³

そのためには本来$u(x,t)$だけでなく、その微分である$u_t$や$u_{xxx}$も$\tau$関数から直接計算する必要があるのですが、$u_{xxx}(x,t)$は$\log(\tau)$の$x$に関する5階微分なので、ちょっと計算は面倒です。
なので今回は直接数値的に計算してしまいましょう。¹⁴

すなわち次の公式を用います。

\begin{align}
& u_x(x,t) = \dfrac{u(x,t+\Delta t) - u(x,t-\Delta t)}{2\Delta t} + \mathcal{O}(\Delta t^2) \\
& u_x(x,t) = \dfrac{u(x+\Delta x,t) - u(x-\Delta x,t)}{2\Delta x} + \mathcal{O}(\Delta x^2) \\
\nonumber & u_{xxx}(x,t) = \dfrac{u(x+3\Delta x,t) - u(x-3\Delta x,t)}{8 \Delta x^3} - \dfrac{ u(x+2\Delta x,t) - u(x-2\Delta x,t) }{\Delta x^3} \\
& \qquad\qquad + \dfrac{13}{8} \dfrac{ u(x+\Delta x,t) - u(x-\Delta x,t)}{\Delta x^3} + \mathcal{O}(\Delta x^2).
\end{align}

この辺りは私より詳しい方が多いはずなので説明は省略します。

すると残差項があるため、$u$がKdV方程式の解であっても、$\Delta_{\mathrm{KdV}}[u](t)$は一般に$\Delta x^2$程度の大きさがあります。ですので、実際にこれが$\Delta x$や$\Delta t$を小さくした時に、$0$に近づく事を確認する必要があります。
それを確認したものが次のグラフになります。グラフは片対数、すなわち縦軸が$\Delta_{\mathrm{KdV}}[u]$の対数、横軸が時刻$t$で、３つのグラフが上から順に$\Delta x=\Delta t =0.1,0.01,0.001$である事に注意すると、見事に$\Delta x^2$で$0$へ収束する事が十分期待できると思います。

実際には様々な$n$と$p,\theta$についてこの事実を確認する必要がありますが(そしてこれは当然ですが数学的証明ではありません)、まあ(書いている私も疲れるので)いいでしょう。

$n$-ソリトン解

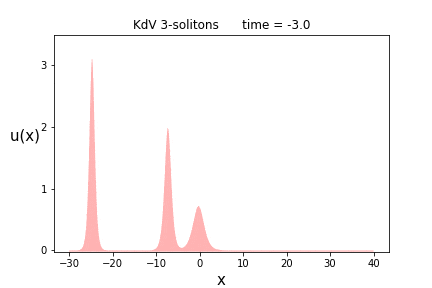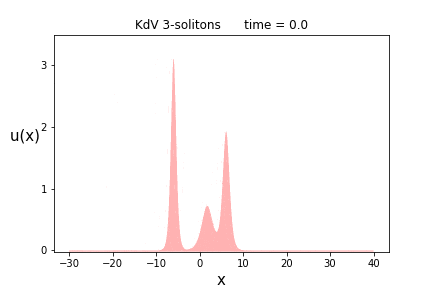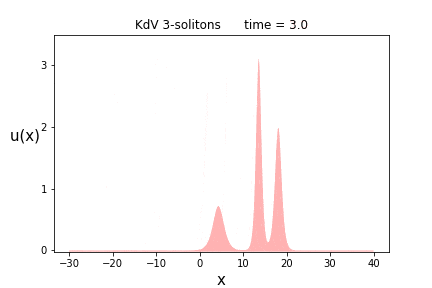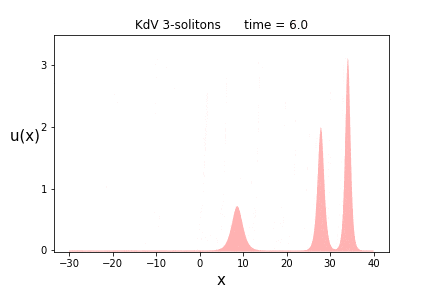
さて、お待ちかねの$n$-ソリトン解の御姿を拝見いたしましょう。
まずは$n=3$です。解の(スペクトラル)パラメータは$p$は前節の場合に等しく($p = \{ 1.2, 2.0, 2.5 \}$)、位相パラメータ$\theta = \{ 0.0, 5.0, -15.0 \}$)に置いています。

もうお分かりだとは思いますが、ソリトンの高さが高いほど、その進む速さも速いです。
実際、1-ソリトン解を見て分かる通り、速さ$v$のソリトンの高さは$\frac{v}{2}$になります。

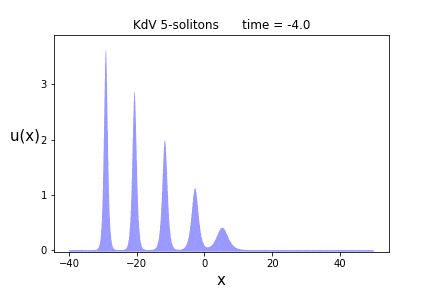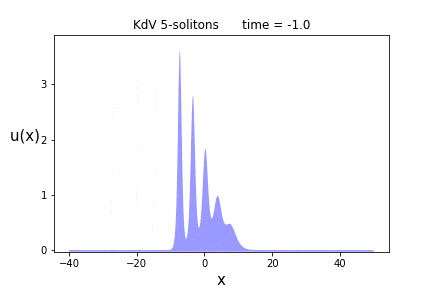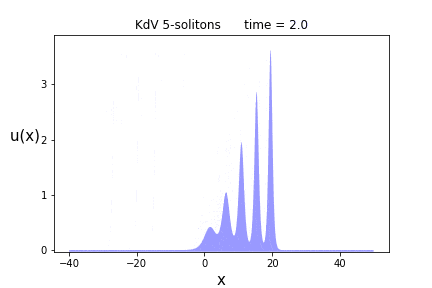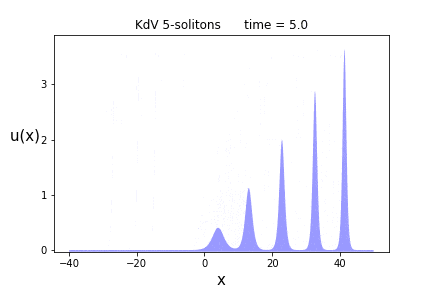
次は$n=5$です。
今度はまとめてぶつけてみましょう。ここで解のパラメータは$p = \{0.9, 1.5, 2.0, 2.4, 2.7\}$と$\theta = \{ 0.0, 0.0, 0.0, 0.0, 0.0 \}$に選びました。

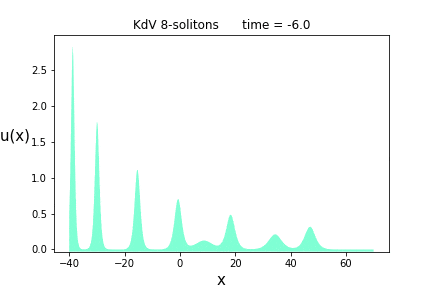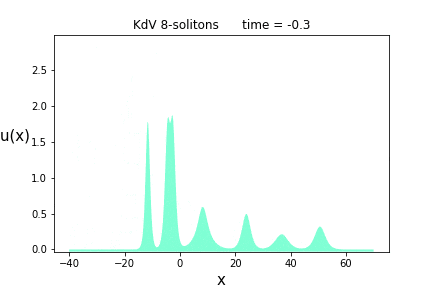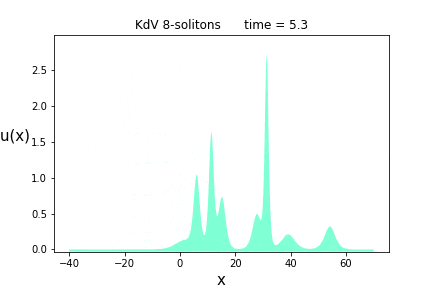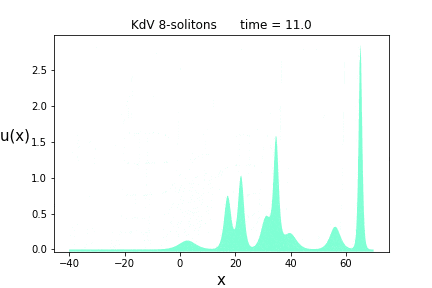
次は$n=8$です。解のパラメータは$p= \{ 0.5, 0.65, 0.8, 1.0, 1.2, 1.5, 1.9, 2.4 \}$と$\theta = \{ 0.0, 10.0, 20.0, 10.0, 0.0, -10.0, -20.0, -10.0 \}$です。

癒やされますね。

相互作用による位相のズレ(phase shift)

最後にソリトン間の衝突(というか追突？追い越し？...)について一言コメントしておきます。

以下のアニメーションをご覧ください。

これは追い越し前の各ソリトンの頂上を基準に、一定速度で進行した場合に、どの位置にいるか、を表したものです。散乱後に想定位置からずれているのがお分かりかと思います。

余談：$\tau$関数の様々な表示

先に$\tau$関数は他にも次のような表示が存在します：

＊逆散乱表示

\begin{align}
\tau^{(n)}(x,t) = \det_{1\le i,j \le n}\left( \delta_{i,j} + \dfrac{2(p_ip_j)^{1/2}}{p_i + p_j}e^{\eta_i(x,t)} \right).
\end{align}

＊Wronskian表示

\begin{align}
\tau^{(n)}(x,t) = \det_{1\le i,j \le n}\left( \dfrac{\partial^j}{\partial x^j} f_i(x,t) \right).
\end{align}

ここで$f_i(x,t) := 2\cosh[ \tfrac{1}{2} ( p_i x - p_i^3 t + \theta_i + \delta_i^{(n)} ) ]$かつ$\displaystyle e^{\delta_i^{(n)}} := \prod_{\substack{ 1 \le j \le n \ j \neq i}} \dfrac{p_j - p_i}{p_j + p_i}$です。
なお、$\tau$関数は以前述べた通り$e^{\alpha x}$をかける自由度(``gauge自由度")があり、一意に定まらないことに注意してください。

ちなみに$n=4$くらいまでは計算機を用いて等価性を簡単にチェックできると思いますので、興味ある方はやはり確認してみてください。

進んだ注：ソリトン解に潜む対称性

進んだ注：ソリトン解に潜む対称性

保存量

KdV方程式が前節で見たような解析解を持つのはなぜでしょうか。
これは数学的に「無限次元の対称性」が存在するから(前節の「進んだ注」参照)、というのが簡潔な一つの答えなのですが、洗練されすぎてて明確な答えにはなっていません。¹⁵

ここでのKdVにおける保存量とは、各時刻$t$において$u$から計算される量で、実際は$t$の値に依らない量の事を言います。¹⁷

まず$u$の局所的な汎関数というものを考えます。
ここで局所的とつけているのは、時刻と位置$(t,x)$を指定すると値が決まる事を強調するためです。
また汎関数とは、関数を引数に取る関数の事で、特に今回の場合、
$u$とその有限回微分$\tfrac{\partial^k}{\partial x^k} u$($k=1,2,3,\ldots$)の多項式(微分多項式と呼ぶこともある)で書けるものとします。
もし関数解析などをご存じの方は、これが線形でない事に注意してください。
局所的な汎関数の例としては、$u$はもちろん、$uu_xu_{xx}$や$u^2 + u_x^3$などいろいろ考えられます。

さてこの局所的な汎関数$q[u](x,t)$から、$x$に依存しない$t$だけの関数(かつ$u$の汎関数でもある)を次のように積分で構成しましょう。

\begin{align}
Q(t)=Q[u](t) = \int^{\infty}_{-\infty} dx\; q[u](x,t)
\end{align}

この量$Q$が$t$に依存しない定数である時、すなわち$\dfrac{d}{dt} Q(t) = 0$を満たす時、(KdV方程式の)保存量と呼びましょう。また$Q$が保存量の時、物理学の用語を流用して$q$を電荷密度と呼ぶ事にしましょう。

定義したので早速例を見てみましょう。実は$q[u] = u$は電荷密度であり、$Q_1 := \displaystyle \int dx u(x,t)$は保存量です。
これが保存量であることはKdV方程式を用いて

\begin{align}
\dfrac{d}{dt} Q(t) = \int^{\infty}_{-\infty} dx \tfrac{\partial}{\partial t}u(x,t)
 = -\int^{\infty}_{-\infty} dx \tfrac{\partial}{\partial x} [ 3u(x,t)^2 + u_{xx}(x,t) ] \\
 = - \lim_{x \to \infty} [ 3u(x,t)^2 + u_{xx}(x,t) ] + \lim_{x \to -\infty} [ 3u(x,t)^2 + u_{xx}(x,t) ] = 0
\end{align}

ここでKdV方程式が$u_t + (3u^2 + u_{xx})_x = 0$と書き直せる事と、$\displaystyle \lim_{ x \to \pm \infty} u(x,t) = 0$や$\displaystyle \lim_{ x \to \pm \infty} u_{xx}(x,t) = 0$を用いました。物理をご存じの方は$3u^2 + u_{xx}$が電流密度(カレント)に対応する事が解ると思います。

また

\begin{align}
uu_t = -(2u^3)_x - (uu_{xx})_x + u_xu_{xx} = - (2u^3 + uu_{xx} - \tfrac{1}{2}u_x^2)_x
\end{align}

より、$\displaystyle Q_2 := \int_{-\infty}^\infty dx; u^2(x,t)$も保存量である事が分かります。

なおここまでで勘の良い方は、$q[u]$が電荷密度、すなわち$Q[u]$が保存量であるためには、ある$u$の局所的汎関数$j[u]$で$j[u \equiv 0] = 0$を満たすものが存在して、

\begin{align}
\dfrac{\partial}{\partial t} q[u] = - \dfrac{\partial}{\partial x} j[u]
\end{align}

が成立すれば良い、という事がお分かりだと思います。例えば２つ目の例では、$j[u] = 2u^3 + uu_{xx} - \tfrac{1}{2}u_x^2$です。

では他に保存量はないのでしょうか？
実は独立な保存量が無限個存在する事が知られています。例えば

\begin{align}
Q_3 := \int_{-\infty}^\infty dx\; ( u^3 - \tfrac{1}{2}u_x^2 )
\qquad
Q_4 := \int_{-\infty}^\infty dx\; ( u^4 - 2 uu_x^2 + \tfrac{1}{5}u_{xx}^2 )
\end{align}

なども保存量である事が示せます。これらの保存量の導出については『余談：保存量の導出』で行います。

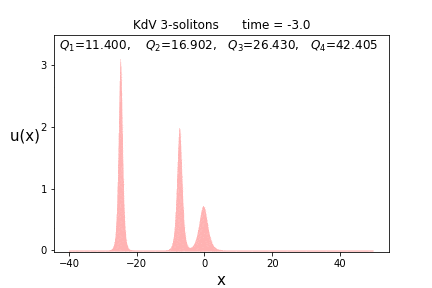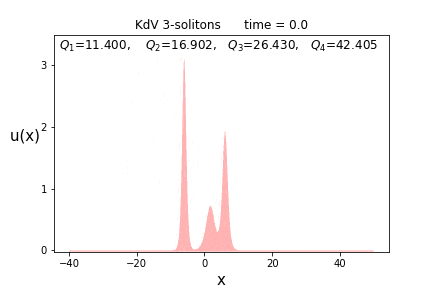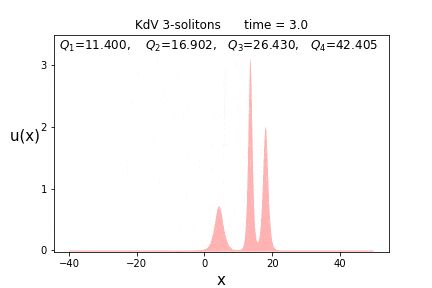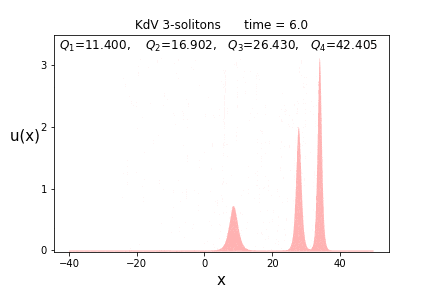
実際にこれらの保存量の値を先の3-ソリトン解の場合の数値計算してみた結果が以下です。

上に記した四つの値が各時刻に(数値的に)計算した積分値です。$t$が変化してもほとんど変わらない事が分かるでしょう。
これが実際に保存量になっていることは、数値計算が上手くいっているかの重要な判断指標にもなります。

余談：保存量の導出

余談：保存量の導出＆進んだ注：Miura変換を経て散乱問題へ

箱玉系

前章では、KdV方程式と、その解であるソリトンについて見てきました。本章では、このKdV方程式の記述する系をある種「離散化」した、箱玉系について考えていきます。

一般に箱玉系、というと無限系で定義するのが普通なのですが、今回は周期系にのみ限定します。

定義

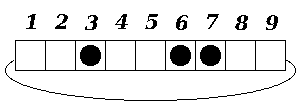
まずは下図のように$1$次元上に、$L$個の箱を周期的に並べてみましょう。ただし各箱は空(□)またはボール(●)が$1$個入っています。

本章で考えるのは、このような箱と玉だけ構成される単純なシステムです。
そのままですが、これを箱玉系(box-ball-system)と呼びます。

まずはイメージをつけるために以下のアニメーションをご覧ください。

ここで箱の数は変わっておらず、玉の位置だけが変化している事に注目してください。このような玉の並びの事を箱玉系の状態と呼びます。
空の箱は$0$、ボール入の箱は$1$で表す事にすると、状態は$0$と$1$から成る$L$個の列($i$番目の箱の有無が$i$列目に対応)で表すことができます。¹⁸

上の例ですと、$\{001001100\} \in \Omega_9$ ($L=9$)になります。

また時間の概念も存在しますが、KdV方程式の表す系が時刻について連続的であったのに対し、箱玉系では離散的です。つまり$t$を時刻とした時、$t$は整数値のみ取ります。スナップショットをとってるようなものだと理解してください。よって以後、「時刻$t+1$は時刻$t$の$1$ステップ後」、と言ったような表現をする事にします。そして各時刻には上記の状態がそれぞれ割り当てられます。
時刻$t+1$の状態は、時刻$t$の状態から一意に決まるのですが、この具体的な規則については後で述べます。

また始まりの時刻を$t=0$としましょう。特に始まりの時刻の状態を初期状態(initial state)と呼びます。

実は後述する時間発展規則は状態空間に作用する全単射(可逆)であるため、負の時刻(すなわち過去)を考える事もできますが、ここでは考えない事にします。

さてもう少し数学的に表現してみましょう。まず時刻$t$での状態を$\varphi(t) = \{ \varphi^t_1 \varphi^t_2 \cdots \varphi^t_L \} \in \Omega_L$と表します。ここで$\varphi^t_k \in \{0,1\}$は時刻$t$における$k$番目の箱の状態を表します。

すると箱玉系は写像$\varphi : \mathbb{Z}_{\ge 0} \longrightarrow \Omega_L$で記述されます。また(可逆な)時間発展とは(全単射な)写像$T : \Omega_L \to \Omega_L$に他なりません。特に定義から$T^s \circ \varphi_{t} = \varphi_{t+s}$が成り立ちます。ここで$T^s := \underbrace{T \circ T \circ \cdots \circ T}_{s}$です。

時間発展規則

さて前節では箱玉系の状態を定義しました。次に時間発展規則について述べましょう。規則を述べるにあたって、箱の数$L$は玉の数に比べてそこそこ大きいとしておきますが、あまり気にしないでください。

先に述べた通り、時刻$t+1$の状態は、ある規則に従って時刻$t$の状態から一意的に決まるのですが、この規則の事を「箱玉系の時間発展規則」と呼ぶ事にします。これを与える事は$T$を与える事と他なりません。ここでは、運搬車(玉をたくさん積み込めるトラックだと思ってください)と呼ばれる概念を用いて、この箱玉系の時間発展規則を定めたいと思います。

運搬車は、どの箱の前に入るか、という位置情報と、玉を何個積んでいるか、という積載情報の２つを持っています。あくまで説明の便宜のため導入した概念であり、箱玉系の状態にこれらの情報は含まれない事に留意してください。

さらに説明を分かりやすくするため、時間発展規則を説明する際は、各箱の状態として「玉が１個入っている」、「空いている」に加えて、「封鎖してある」(中身はどちらでも良い)状態を導入します。

さて$\varphi^{t}$から$\varphi^{t+1}$を決めるにあたって、時刻$t$で一旦時を止めます。しかしこの間に運搬車は自由に動け、玉の積み下ろしも自由に行えるとします。

また最初、全ての箱は封鎖していない状態にあるとします。後でアニメーションも置いておきますので、適宜ご参照ください。

まず$1$番目の箱の前に、運搬車を止めます。この時、運搬車は何も積んでいません。もし$1$番目の箱に玉がある場合、その玉を回収し、運搬車に積み込んだ後、$1$番目の箱を封鎖してから次の箱へ移動します。もし玉がない場合は、何もせず、次の箱へ向かいます。

次に$2$番目の箱の状態も、玉がある場合とない場合の$2$通りが考えられます。玉があった場合はやはりそれを積み込み、封鎖してから次の箱へ移動します。箱に玉がなかった場合はどうでしょうか？もし$1$番目の箱にも玉がなかった場合、運搬車に玉を積んでいないため、やはり何もせず次の箱へ向かいます。しかし$1$番目の箱で玉を回収していた場合、運搬車には玉が$1$個積まれているので、それを積み降ろします。そして積み降ろした後、箱を封鎖して次の箱に行きます。

さて以上の行動を一般的にまとめましょう。まず、$i \in \{1,2,\ldots, L\}$番目の箱に到着したとします。この時、次の$4$通りのケースに分かれます。

• 箱に玉がある場合は、玉を運搬車に積み込んだ後、$i$番目の箱を玉が置けないように封鎖します
• 箱が空で、運搬車に玉がある時、箱へ１個だけ積み下ろした後、箱を封鎖します
• 箱が空で、運搬車に玉がない時、何も行いません
• 箱が封鎖済みの時、何も行いません

いずれかの行動を選択した後、運搬車は$i+1$番目の箱へ移動します。ただし$i=L$の時、周期性から運搬車は$1$番目の箱へ移動するものとします。

以上のルールを繰り返し行うと、いずれ全ての玉が移動済み(封鎖された箱に入っている状態)で、かつ運搬車に玉が積まれていない状態になります。この時、時刻を$t$から$t+1$に増やします。そして封鎖していた箱を全て開放すると、この時の状態が、時刻$t+1$の箱玉系の状態になります。

この時間発展規則は決定的であり、時刻$t$の状態$\varphi_t$から時刻$t+1$の状態$\varphi_{t+1}$は一意に定まります。この時間発展規則を箱玉系の状態空間$\Omega_L$上の写像とみなし、$\varphi_{t+1} = T(\varphi_{t})$とも表現できます。なお(何度か先走って使っているのですが)、この写像$T : \Omega \to \Omega$は全単射である事が証明でき、この事実を、時間発展規則は可逆的である、と言います。

最後に玉数について考えてみます。$\displaystyle M := \sum_{i=1}^{L} \varphi^t_i \in \mathbb{Z}_{\ge 0}$
とおくと、これは玉の全個数を表します。上述の規則から、これは時間発展のもとで不変です。

そして察しがいい方は気づいておられたかもしれませんが、上述の規則が成り立つためには、$M \le \dfrac{L}{2}$が実は必要でした。
以降、これを仮定しましょう。¹⁹

シミュレーション

上述の時間発展規則に従う箱玉系の例を幾つか眺めてみましょう。

例１

シンプルですね。5個連なった玉の塊がまとめて移動しているだけです。

例２

今度は4個と2個の塊が動いていますね。4個の方が動く速度が速いので、途中で2個を追い越しているのが解ると思います。
ここで追い越した後も4個と2個の塊を保っている事に注目してみましょう。この性質は前章で見たKdV方程式のソリトンと類似しています。
すなわち、この連続する玉の塊こそが箱玉系におけるソリトンなのです。

形が崩れないのは偶々玉だけにであろう、と疑い深い方のために、もう少し例をお見せしましょう。

例３

例４

例５

保存量

上記の箱玉系にも保存量があります。箱玉系における保存量を、状態から計算できる数学的対象(集合)で、時間発展の元で不変なものと定義しましょう。すなわち$X$を適当な数学的対象として、写像$Q : \Omega_L \longrightarrow X$で、写像の等式として$Q \circ T = Q$を満たすものを、箱玉系の保存量と呼ぶ事にします。

例えばボールの数$M$は時間発展の元で変わらないので、これは保存量で、この時$X = \{0,1,2,\ldots,L/2\}$です。しかしながら箱玉系にはより詳細な情報を持った不変量が存在することが知られています。この事について説明しましょう。

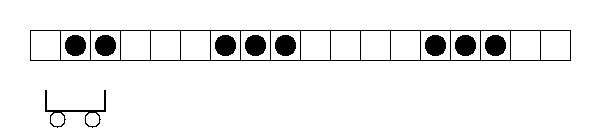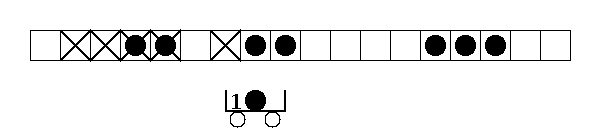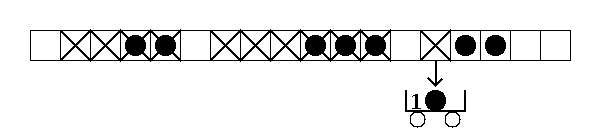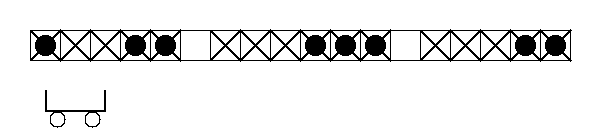
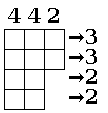
まず$\phi_1 = \varphi^t$とおきます。下図の例では、$\phi_1 = \varphi = \{001110011000111001100000\}$です。

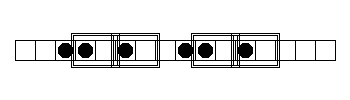
ここで$10$の順番で並び合っているもの(上図の二重矩形で囲んだ領域)に着目します。(系は周期的であるので、$L$番目の箱の右隣は$1$番目の箱である事に注意してください。)このペアの個数を数え上げると、$4$個になります。そしてこの4つのペアを取り除きくと、以下のようになります。

ここで対応するビット列を$\phi_2$とおくと、$\phi_2 = \{0011010011010000\}$です。この時$10$のペアは$4$個ありますが、再びこれを取り除きましょう。新しい状態を$\phi_3$とおくと、$\phi_3 = \{00101000\}$であり、下図のようになります。

最後に残ったペア$2$個を取り除くと、玉がなくなるのでここで終了です。これまでに数えたペアの数は順番に$4,4,2$でした。

この数分だけの箱を左から列毎に下図の並べたものが保存量となります。この図形をYoung図形と呼び、$X$はYoung図形の集合、という数学の対象になります。

さらに一番上の行から箱の数を順番に読み取ってみましょう。すると$3,3,2,2$という数列が得られますが、これはまさに連続する玉の塊の数になっています。

以上を一般の場合にまとめ直すと、

• まず$\phi_1 = \varphi^t$とおき、$i=1$とします
• ビット列$\phi_i$に対し、$``10"$対の数を数え上げ、$p_i$とします
• 前ステップで見つけた$``10"$対を取り除き、新しい列を$\varphi_{i+1}$とします
• 新しい列に$1$が含まれていたら$i$を1増やしてステップ2に戻ります
• $j$列目に$p_j$個の箱を縦に並べます

このようにして、箱玉系の状態$\Omega_L$からYoung図形の集合$\mathcal{Y}$への写像が構成できました。これが実際に時間発展の下で不変である事の証明は、今回行いませんが、様々な例で計算してみてください。時間発展で不変である事が分かります。

基本周期

さて、ある箱玉系の状態$\varphi \in \Omega_L$が与えられた時、その軌道$\mathcal{O}_{\varphi} := \{ T^{; n}(\varphi) ;|; n \in \mathbb{Z}_{\ge 0} \}$を考えてみましょう。これは状態$\varphi$を初期状態とした時、時間発展によって取りうる状態を列挙したものです。$\Omega_L$は有限個の要素から成る有限集合であり、軌道$\mathcal{O}_\varphi$は状態空間の部分集合ですから、明らかに有限集合です。

先に挙げた例からも分かる通り、有限個の集合ということは、ある時刻$t=T_{\varphi}$に初期状態$\varphi$へと戻ってきます。実際に上記例では準に、例１が$T_{\varphi} = 18$、例２が$T_{\varphi} = 15$、例３が$T_{\varphi} = 216$、例４が$T_{\varphi} = 72$、例５が$T_{\varphi} = 24$です。アニメーションはこの時刻まで作ってありますので、お暇な方は眺めてみてください。

この$T_{\varphi} := \min \{ n \in \mathbb{Z}_{> 0} | T^n(\varphi) = \varphi \}$を、箱玉系の状態$\varphi$に対する基本周期と呼びます。なお、明らかに$T_{\varphi} = T_{T^k(\varphi)}$ (下付き部分の$T$は時間発展の写像)が任意の$k \in \mathbb{Z}$について成立します。

以上が、箱玉系の基本的事項になります。
本当はここから箱玉系の基本周期の分布を議論するために、$L$が$30$位になると計算時間の問題から安直に計算できない事、そして計算する公式(証明はしない)を話す予定だったのですが、時間の制約上、割愛させて頂きます。

なお『進んだ注：Riemann予想との関係』をpdf版には追加予定ですので、興味がある方はご覧ください。

まとめ・書けなかった事項を学ぶための参考文献

以上、駆け足ではありましたが、ソリトンの世界をほんの少しだけご紹介しました。

自然現象から発見された概念でありながら、計算機の登場によりその普遍性が認識され、そして背後に豊かな数理構造を持つ、まさに数理物理学の申し子と言うべき存在だと私は思っています。何より($1+1$次元ではあるが)連続な世界で発見されたソリトンは、完全デジタルな離散世界にも姿を表し、離散世界の真理を暴きだす手助けをしてくれているようにも見えます。

例えばKdV方程式、箱玉系共に、$\mathfrak{sl}_2(\mathbb{C})$や$\hat{\mathfrak{sl}}_2(\mathbb{C})$というLie代数と(複数の)関係がある事はその一つの現れでしょうか。

さて、時間の制約、私の力量・理解不足から書ききれなかったトピックが大量にあります。参考文献と合わせて提示しておきましょう。

1.

KdV方程式ですと、逆散乱法・擬微分作用素の話はどちらも中心となるトピックです。特に後者は、pdf版『進んだ注：ソリトン解に潜む対称性』で導入した無限個の変数(解の変形パラメータ)で微分した際の微分方程式や、『進んだ注；保存量の導出』で導いたKdV方程式の無限個の保存量を、統一的に理解する道具となります。

逆散乱法については『非線形波動』(和達三樹著)が非常にまとまっていて物理系の人には読みやすいですし、後ろの方では量子可積分系と結び目の話も書かれていて、一冊ニ眺です。数学系の方には、『ソリトン理論とハミルトン形式(上)』(Ludwig Faddeev, Leon Takhtajan著)(英語タイトルは``Hamiltonian Methods in the Theory of Solitons")か『KdV方程式』(田中俊一・伊達悦朗著)を挙げておきます。前者は、非線形Schr"odinger模型をベースに古典的な可積分系を意識して割とかっちりしていますが、アイデアが分かりにくいです。
後者はAbel写像や準周期解との関係を述べている、数少ない日本語で読める本です。

ちなみに世界的には``Solitons and the Inverse Scattering Transform"(Mark J. Ablowitz・Harvey Segur著)(翻訳も見た気がします)をよく目にしますが、分厚くて私もあまり読んでいません。

擬微分作用素については、例えば『ソリトンの数理』(三輪・伊達・神保著)辺りが詳しいと思います。逆散乱法と併せて書いてあるものとしては、Graeme Segalの``Integrable systems and inverse scattering"が簡潔で読みやすいです。

一方で箱玉系ですと、Riemann予想(Chebyshev関数の漸近評価版)とのつながりは勿論、量子群の表現論とKKR写像、といったテーマとの関連が面白いと思っています。これについては例えば『箱玉系の数理』(時弘哲治著)、『ベーテ仮説と組合せ論』(國場敦夫著)、数理物理サマースクール2011講義録の「箱玉系の可積分性ークリスタルとトロピカル幾何」(井上玲著)をご参照ください。また超離散の話は『差分と超離散』(広田良悟・高橋大輔著)が丁寧かつ詳しいです。

2.

一方で、本年は戸田格子提唱50周年記念(残念ながら素数ではありません)にあたりますので、本当はこの戸田格子をご紹介したかったのですが、ソリトンの話をするならやはりKdV方程式と箱玉系は外せない、と思いましたので、今回は割愛させて頂きます。
戸田格子についてはまた機会がありましたら、いずれ解説したいと思いますが、書籍としては、発見者の戸田先生が本をたくさん書かれているので、それらのどれかを参照すると良いと思います。

3.

最後は『位相的ソリトン』です。これは現代物理学の最重要成果の一つである場の量子論で重要な役割を果たします。インスタントン(instanton)やモノポール(monopole)、量子渦(例えば第二種超伝導状態で実現)もソリトンの一種です。²⁰

1. 量子論をご存じの方は、所謂「波と粒子の二重性」と混同しないようにしてください。全く別物です。
   実際に、ソリトンの英語スペルはsolitonであり、これはsolitary(孤立した)+on(粒子につける接尾辞)から来ています。² ↩

2. KruskalとZabusky(『ソリトンの夜明けまでの簡単な歴史』参照)により名付けられました。本来はsolitronという名前が候補だったらしいですが、同名の電気素子会社が存在していたのでやめにしたそうです。(Ref. 数理科学`80-5『場の理論におけるソリトン』和達三樹) ↩

3. もしこれは、という動画を見つけた方は是非ご一報ください。(実はあんまりないですよね、solitonの良い動画...) ↩

4. このKdV方程式を一般化したKP方程式の解空間は佐藤-Grassman多様体、あるいは普遍Grassmanianなどと呼ばれている対象になっています。そしてKdV方程式の解はこのKP方程式の解を(2-)簡約(パラメータの特殊化)したものになっています。この片鱗は『進んだ注：ソリトン解に潜む対称性』を参照してください。 ↩

5. ↩

6. ちなみに前半は連続な系、後半は離散な系ですが、両者は共通の方程式(離散KdV方程式)から、それぞれ連続極限と超離散極限で姿を表します。詳細は例えば『箱玉系の数理』(時弘哲治著)を参照してください。 ↩

7. 正確にはソリトン自体も数学の諸分野と関連しています。特に位相的ソリトンと呼ばれる対象はベクトル束やK理論と関わりがあります。これに関しては最後に文献を紹介する予定です。
   うち幾つかの分野との関係の片鱗も少しばかり紹介したいな、という事で、「進んだ注」という形でpdf版では軽く触れました。これら背後に潜む数学の雰囲気だけでも掴んでいただければ幸いです。 ↩

8. 数値計算に関して可積分系がご専門の黒木先生がtwitterこのツイートを含むスレッドにて有益なコメントとJuliaのコード・計算例を紹介してくださっているので、是非そちらも併せてご覧ください。
   これについて見ていきましょう。 ↩

9. 以降この章において、断らない限り全ての変数は実数に値を取るとします。
   この波が、次のKdV(Korteweg-de Vriesの略)方程式(偏微分方程式)に従うとしましょう。¹⁰ ↩

10. KdV方程式の導出方法としては、例えば流体力学と逓減摂動法に基づく導出が知られています。例えば『非線形波動とソリトン』（戸田盛和著）を参照してください。
    ただし、ここで次のような記号を導入しています： ↩

11. 系によってはどれくらいの速さで$0$に収束するか、が解析解の存在に影響してきます。 ↩

12. 具体的には$(i,j)=(1,2),(2,3),(3,1)$について、$a(\theta_i)a(\theta_j)$を$a(\theta_i)a(\theta_j)\left( \tfrac{p_i-p_j}{p_i+p_j} \right)^2$に置き換え、さらに$a(\theta_1)a(\theta_2)a(\theta_3)$を$a(\theta_1)a(\theta_2)a(\theta_3) \times c$と置き変えて、$c$を$p_{i=1,2,3}$について解くだけです。
    紙とペンでやると、心が折れそうになったり、もしくは指関節が痛くなったりするかもしれません。そして次に示す結果を(二重の意味で)自然に受け入れられるようになるでしょう。 ↩

13. 当たり前ですが、計算機上は$x$の取りうる範囲は$\mathbb{R}$の有限部分集合です。 ↩

14. 実際は、5階微分も計算できるように設計していたのですが、直接計算する方が楽だったので、今回はそうしました。 ↩

15. そもそも「無限次元の対称性」が存在するからと言って、解析解が存在するとは限りません。しかしながらこの事実は経験的によく成り立つ事が多いです。
    代わりにここでは、KdV方程式には保存量 や着色料がたっぷり存在する、という事実に焦点を当てます。¹⁶ ↩

16. 有限次元自由度においては、Liouville-Arnoldの定理より「十分な数の」保存量が存在することは、系が「求積的」である事とほぼ同義であり、これが「可積分」の定義です。しかしながらKdV方程式の記述する系は、(例えば、$u$が許される関数空間がvector空間の次元として無限である事から)無限自由度を持ちます。この(=可積分系の)文脈での「無限次元」というのは一般には有限次元でない、以上の意味はなく、万人が納得する(一般的な系での)「可積分」の定義は現時点でありませんし、おそらく存在しません。ただし多くの場合、「解析解が存在する事」と「可積分である事」はほぼ同義である事が多いです。 ↩

17. KdV階層(前節での「進んだ注」参照)における保存量は、無限個の時間の生成子になっています。
    それではより丁寧に保存量の定義$q[u](t,x)$と、その例を見る事にしましょう。 ↩

18. ボールありを$2$、空を$1$で表す流儀もあります。これは各箱の状態を、$A_1$型Lie代数の基本表現のウェイトに対応させた場合に自然な記法です。ちなみに$A_1$型Lie代数を一般の``Lie代数"に置き換えると、対応して箱玉系も一般的なものに置き変わります。詳しくは『進んだ注：KKR対応』を参照してください。}
    すなわち状態は$L$ビット列で表され、全ての可能なビット列の集合は$\Omega_L := \{0, 1\}^L$になります。
    この$\Omega_L$を箱玉系の状態空間(力学系の言葉では位相空間(phase space)とも言います)と呼びます。 ↩

19. この仮定が満たされない場合も(周期)箱玉系は定義可能です。例えば先に挙げた『箱玉系の数理』を参照してください。 ↩

20. これらは数学的には、principal G-budnleの特性類(=cohomology)の代表元としての接続や、適当な切断の組に対応しています。
    超弦理論で姿を表すD-ブレーンも、超重力理論におけるソリトンです。²¹ ↩

21. これも先と同様ですが、こちらはtorsionなども考慮したある種のK理論で記述される事が知られています。
    この辺りの話は例えば、David Tongによる``TASI Lectures on Solitons"が大変良くまとまっていてオススメです。 ↩