3次ベジェ曲線間の交点を高精度で高速に求める手法を提案する。ベジェ曲線の陰関数表示を経由して、交点のパラメータ値を代数的に求める手法であるImplicitization法が知られていたが、この手法における代数方程式の実根を、安定的に効率良く求める手法は確立されていなかった。今回、ブダン・フーリエの定理で候補を絞り、ヴァンサンの定理の応用であるVAG法で実根分離を行い、二分法とリダーズ法によって実根を求める手法を試みた。高次の代数方程式の解法として一般的なDKA法に対し、本手法では根の探索範囲をベジェ曲線のパラメータの値域の実数に限定できること、値域外の根の影響を受けないことがわかった。ベジェ曲線の形状や交差のパターンによって重根となった場合、反復的な求根法(二分法やリダーズ法など)が適用できない、との課題が抽出され、VAG法を拡張し求根にも用いる解決策を考案し有効性を確認した。本手法を C++/Qt 環境において試行実装し、任意に入力された3次ベジェ曲線間の交点を正しく求めることができることを確認し、さらに所要メモリや処理時間等が実用可能なレベルであることを確認した。本手法は対象をベジェ曲線に特化しておらず、他の3次パラメトリック曲線にも適用できると考えられる。
本稿で扱うベジェ曲線間の交点の例を以下に示す。オレンジ色は制御点 ${\boldsymbol{p}}_0, {\boldsymbol{p}}_1, {\boldsymbol{p}}_2, {\boldsymbol{p}}_3$ で定義されるベジェ曲線 ${\boldsymbol{B}}_0$、青色は制御点 ${\boldsymbol{p}}_4, {\boldsymbol{p}}_5, {\boldsymbol{p}}_6, {\boldsymbol{p}}_7$ で定義されるベジェ曲線 ${\boldsymbol{B}}_1$ である。
| 例1 |  |
1点で交差 |
| 例2 |  |
1点で交差 |
| 例3 |  |
9点で交差 |
| 例4 |  |
${\boldsymbol{B}}_0$ が2次 |
| 例5 |  |
${\boldsymbol{B}}_0$ が1次 |
| 例6 |  |
1点で交差 交点で1次微分が一致 |
| 例7 |  |
1点で交差 交点で1次微分が一致 |
| 例8 |  |
1点で接触 交点で1次微分が一致 |
| 例9 |  |
1点で接触 交点で1次微分が一致 |
| 例10 |  |
カスプ点が接触 |
| 例11 | 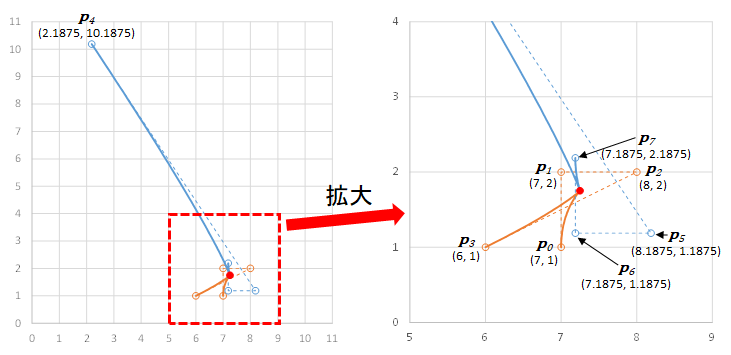 |
カスプ点どうし接触 |
背景と関連研究
ベジェ曲線はコンピュータグラフィックスやGUI描画、CADなどで広く用いられるパラメトリック曲線である。曲線同士の交点を求める必要性は高い。
交点検出の既存手法としては、曲線を小さな線分に区切って衝突判定を行う折れ線近似法がある。ベジェ曲線を画面に表示するためのレンダリング処理においては、OpenGLなどの描画APIでは曲線の描画はサポートされていないため、その上位(Qt GUIやCairoなど)でベジェ曲線は折れ線に近似変換される。その折れ線情報を衝突判定に流用して交点検出ができるため、折れ線近似による交点検出は合理的であると言える。交点の位置精度も、レンダリング処理では画素単位かその数分の一程度で十分である。
一方、CADその他においては、交点検出だけのためにベジェ曲線を折れ線に近似変換することは効率が悪く、求められる精度も高いことから、折れ線近似法は不向きである。このような用途では、ベジェ曲線は制御点に外接するポリゴンに内包される性質を用いて、ポリゴンどうしの交差から交点が含まれる曲線の範囲を限定し、分割して切り出されたサブ曲線に対し、同様の処理を反復して交点を絞り込むサブディビジョン法が用いられてきた。サブディビジョン法の例として、T. W. Sederbergと西田友是が提案したベジェクリッピングが知られている。[1]
しかし、この手法はベジェ曲線の形状や交差のパターンによっては収束性が悪かったり、精度の保証が難しかったりする場合がある。
T. W. Sederbergらは、ベジェ曲線を陰関数化して代数方程式(3次ベジェ曲線どうしの交差であれば9次式)に変換し、解を求めるアプローチであるImplicitization法を提案した。[2][3]
Implicitization法では、パラメトリック形式のベジェ曲線を陰関数に変換し、もう一方の曲線のパラメトリック関数を代入することで代数方程式(陰伏方程式)を得て、これの実根、すなわち交点のパラメータを求める。この手法はベジェ曲線の形状や交差のパターンの影響を受けにくく、効率良く高い精度で交点位置が求められると期待されるが、陰伏方程式を解く適当な方法は示されていなかった。そこで今回、Implicitization法のアプローチをベースに、陰伏方程式を効率良く安定的に解く手法を検討し、ベジェ曲線の交点を求めるための実用的な実装を実現することを目指した。
9次方程式は代数的に解くことができないため、反復的な求根法により近似解を求める必要がある。ニュートン・ラフソン法をベースに、高次方程式に対応したDKA法が一般に知られている。
DKA法は複素根に対応しており、複素平面上で根を包含する円周上に初期値を等間隔で配置し(Aberthの初期値)、近似計算を反復する。複数の近似解がひとつの根に収束しないよう、近似解どうしの差が漸化式の計算に反映されるしくみ(斥力の作用)が備わっている。初期値を配置する円の半径はAberthの方法により正しく設定する必要がある。半径が小さすぎると収束計算において不安定な挙動が発生し、大きすぎると収束が遅くなる。
最初に、陰伏方程式の実根をDKA法で求めることを試みた。DKA法の実装は、文献[4]を参考にExcel上に評価ワークシートを構築した。ただし、初期値の円の半径は文献[5]のプログラムを用いて求めた値を用いた。
すべての根が $(0,1)$ の実数であるサンプルに対しては、良好な収束が得られた。冒頭の例3がこれにあてはまる。
| $F_0(u)=0$ の根 | $F_1(t)=0$ の根 |
|---|---|
| 0.0192470 0.0549916 0.122057 0.320989 0.442531 0.488156 0.900476 0.944674 0.963072 |
0.0705391 0.0972454 0.151318 0.423317 0.504785 0.616234 0.858628 0.947328 0.966598 |
初期値の円の半径は 0.891145 と 0.815073 と小さく、DKA法は15回程度の反復で収束した。
ところが、曲線の交差パターンによってベジェ曲線のパラメータの値域から大きく外れた根(交点検出には不要な根)が含まれる場合には、初期値の円が巨大化して収束性が大幅に悪化した。冒頭の例1がこれにあてはまる。
| $F_0(u)=0$ の根 | $F_1(t)=0$ の根 |
|---|---|
|
-567116 0.557665 1.61807 5.16799 5.79814 -0.570942-0.800873*I -0.570942+0.800873*I 283560-491136*I 283560+491136*I |
-248197 -1.03331 0.446194 1.86453 2.90335 -213844-446352*I -213844+446352*I 0.534608-0.882298*I 0.534608+0.882298*I |
初期値の円の半径は 624194 と 518608 と巨大であり、DKA法は50回反復しても収束しなかった。これら試行の結果、DKA法は本用途には不向きとの結論に至った。
NVIDIAのAlexander Reshetovは、多数のベジェ曲線でモデリングされたPBRTのhairやfurを対象としたレイトレーシングにおいて、実根分離を先に行い、実根が唯一含まれる区間を特定してから反復的な求根法を適用するアプローチを発表した。[6]
- 3次ベジェ曲線と光線(直線)の交点を求める。ベジェ曲線を太さのあるものとして扱う必要があり、曲線と直線の間隔の2乗(6次関数)が最小になる位置を求めるため、その微分(5次関数)の根を求める。
- 根を求めるため、ブダン・フーリエの定理により絞り込んでヴァンサンの定理により実根を分離し、求根アルゴリズムをなるべく反復なしで適用する。
- ベジェ曲線と直線の空間的な関係性から根の存在する範囲を絞り込む、等のテクニックを組み合わせることにより、リダーズ法反復なし1回とセカント法の組み合わせで十分な近似精度が得られる。
- 既存の方式(折れ線近似)に比較し、パフォーマンス、精度とも大幅に向上する。
今回、これにヒントを得て、同様のアプローチをベジェ曲線どうしの交点検出に適用することを目指した。ヴァンサンの定理には、VAS法、VCA法、VAG法などの応用アルゴリズムがあり、今回は実装が容易なVAG(Vincent–Alesina–Galuzzi)法を選択した。また、実根分離された区間に対する反復的な求根法は、二分法で範囲を絞り込んでからリダーズ法を適用するようにした。重根については二分法やリダーズ法が対応していないため、VAG法を拡張して適用した。
採用した手法
対象の曲線
制御点 ${\boldsymbol{p}}_0, {\boldsymbol{p}}_1, {\boldsymbol{p}}_2, {\boldsymbol{p}}_3$ で定義されるベジェ曲線 ${\boldsymbol{B}}_0$ 上の任意の点の座標 $(x,y)$ は、以下の行列形式のパラメトリック関数で定義される。[7]
\begin{array}{l}
x=f_0(t)=
\begin{bmatrix}
t^3 & t^2 & t & 1
\end{bmatrix}
{\boldsymbol{R}}_{bz}
\begin{bmatrix}
p_{0x} \\
p_{1x} \\
p_{2x} \\
p_{3x}
\end{bmatrix}
=a_0t^3+a_1t^2+a_2t+a_3
\\
y=g_0(t)=
\begin{bmatrix}
t^3 & t^2 & t & 1
\end{bmatrix}
{\boldsymbol{R}}_{bz}
\begin{bmatrix}
p_{0y} \\
p_{1y} \\
p_{2y} \\
p_{3y}
\end{bmatrix}
=b_0t^3+b_1t^2+b_2t+b_3
\end{array}
同様に、制御点 ${\boldsymbol{p}}_4, {\boldsymbol{p}}_5, {\boldsymbol{p}}_6, {\boldsymbol{p}}_7$ で定義されるベジェ曲線 ${\boldsymbol{B}}_1$ 上の任意の点の座標 $(x,y)$ は;
\begin{array}{l}
x=f_1(u)=
\begin{bmatrix}
u^3 & u^2 & u & 1
\end{bmatrix}
{\boldsymbol{R}}_{bz}
\begin{bmatrix}
p_{4x} \\
p_{5x} \\
p_{6x} \\
p_{7x}
\end{bmatrix}
=c_0u^3+c_1u^2+c_2u+c_3
\\
y=g_1(u)=
\begin{bmatrix}
u^3 & u^2 & u & 1
\end{bmatrix}
{\boldsymbol{R}}_{bz}
\begin{bmatrix}
p_{4y} \\
p_{5y} \\
p_{6y} \\
p_{7y}
\end{bmatrix}
=d_0u^3+d_1u^2+d_2u+d_3
\end{array}
ただし、${\boldsymbol{R}}_{bz}$ は3次ベジェ曲線固有の係数行列であり;
{\boldsymbol{R}}_{bz}=
\begin{bmatrix}
-1 & 3 & -3 & 1 \\
3 & -6 & 3 & 0 \\
-3 & 3 & 0 & 0 \\
1 & 0 & 0 & 0
\end{bmatrix}
である。
要件定義:パラメータの値域
複数のベジェ曲線が連結された複合ベジェ曲線を想定し、ベジェ曲線のパラメータ($t$ や $u$)の値域は、半開区間 $[0,1)$ とする。ブダン・フーリエの定理やヴァンサンの定理は開区間を対象としているため、$0$ が根であるか判定するロジックを別途追加する。

なお、孤立したベジェ曲線で値域を閉区間 $[0,1]$ とする場合は、$1$ が根であるか判定するロジックを別途追加するものとする。
要件定義:曲線の交差パターンと陰伏方程式の根の類型化
以下は経験則による分類であり、今後解析的な検討・検証を要する。
- 曲線が交差していなくても、他方の曲線を延長すると交差する場合、陰伏方程式は $[0,1]$ の実根を持つ
- 曲線の交点で、両者の1次微分が一致している場合、陰伏方程式は重複数3の重根を持つ
- 曲線どうしが1点で接している(両者の1次微分が一致している)場合、陰伏方程式は重複数2の重根を持つ
- カスプ点が曲線と接している場合、陰伏方程式は重複数2の重根を持つ
- カスプ点どうしが接している場合、陰伏方程式は重複数4の重根を持つ
これらを以下の表に示す。表中 "true"、"false"は、$[0,1]$ の実根の有無を表す。
| 曲線#0 | 曲線#1 | 重複数 | 冒頭の例 | ||
|---|---|---|---|---|---|
 |
交差なし | false | false | ||
 |
交差なし 延長すると交差 |
true | false | ||
 |
1点で交差 | true | true | 1 | 例1 例2 |
 |
1点で交差 交点で1次微分が一致 |
true | true | 3 | 例6 例7 |
 |
1点で接触 接点で1次微分が一致 |
true | true | 2 | 例8 例9 |
 |
カスプ点が接触 | true | true | 2 | 例10 |
 |
カスプ点どうしが接触 | true | true | 4 | 例11 |
手順
- 曲線 ${\boldsymbol{B}}_0$ について、$x=f_0(t)$ と $y=g_0(t)$ を陰関数表示 $F_0(x,y)=0$ に変換する。
- $F_0(x,y)=0$ に 曲線 ${\boldsymbol{B}}_1$ の $x=f_1(u)$、$y=g_1(u)$ を代入した陰伏方程式 $F_0(u)=0$ を求める。
- $F_0(u)=0$ の実根($u \in (0,1)$)を求める。
- 根を $x=f_1(u)$ と $y=g_1(u)$ に代入して、曲線 ${\boldsymbol{B}}_1$ 上の交点候補の座標を求める。
- 曲線 ${\boldsymbol{B}}_1$ について、$x=f_1(u)$ と $y=g_1(u)$ を陰関数表示 $F_1(x,y)=0$ に変換する。
- $F_1(x,y)=0$ に 曲線 ${\boldsymbol{B}}_0$ の $x=f_0(t)$、$y=g_0(t)$ を代入した陰伏方程式 $F_1(t)=0$ を求める。
- $F_1(t)=0$ の実根($t \in (0,1)$)を求める。
- 根を $x=f_0(t)$ と $y=g_0(t)$ に代入して、曲線 ${\boldsymbol{B}}_0$ 上の交点候補の座標を求める。
- 交点候補を突き合わせ、ペアになるものが交点。
ベジェ曲線の陰関数化
曲線 ${\boldsymbol{B}}_0$ のパラメトリック関数表示 $x=f_0(t)=a_0t^3+a_1t^2+a_2t+a_3$、$y=g_0(t)=b_0t^3+b_1t^2+b_2t+b_3$ から陰関数表示 $F_0(x,y)=0$ を得る。具体的には[8]を参考に Wolfram Alpha の Eliminate 機能を使用してパラメータ $t$ を消去し、得られた結果を陰関数 $F_0(x,y)=0$ の形に整理する。Appendix AにNotebookと実行結果を示す。
- これにより得られた曲線 ${\boldsymbol{B}}_0$ の陰関数表示は以下の通り:
$F_0(x,y)=a_3^3 b_0^3-a_2 a_3^2 b_0^2 b_1+a_1 a_3^2 b_0 b_1^2-a_0 a_3^2 b_1^3+a_2^2 a_3 b_0^2 b_2-2 a_1 a_3^2 b_0^2 b_2 $
$\qquad -a_1 a_2 a_3 b_0 b_1 b_2+3 a_0 a_3^2 b_0 b_1 b_2+a_0 a_2 a_3 b_1^2 b_2+a_1^2 a_3 b_0 b_2^2-2 a_0 a_2 a_3 b_0 b_2^2 $
$\qquad -a_0 a_1 a_3 b_1 b_2^2+a_0^2 a_3 b_2^3-a_2^3 b_0^2 b_3+3 a_1 a_2 a_3 b_0^2 b_3-3 a_0 a_3^2 b_0^2 b_3+a_1 a_2^2 b_0 b_1 b_3 $
$\qquad -2 a_1^2 a_3 b_0 b_1 b_3-a_0 a_2 a_3 b_0 b_1 b_3-a_0 a_2^2 b_1^2 b_3+2 a_0 a_1 a_3 b_1^2 b_3-a_1^2 a_2 b_0 b_2 b_3 $
$\qquad +2 a_0 a_2^2 b_0 b_2 b_3+a_0 a_1 a_3 b_0 b_2 b_3+a_0 a_1 a_2 b_1 b_2 b_3-3 a_0^2 a_3 b_1 b_2 b_3-a_0^2 a_2 b_2^2 b_3 $
$\qquad +a_1^3 b_0 b_3^2-3 a_0 a_1 a_2 b_0 b_3^2+3 a_0^2 a_3 b_0 b_3^2-a_0 a_1^2 b_1 b_3^2+2 a_0^2 a_2 b_1 b_3^2+a_0^2 a_1 b_2 b_3^2 $
$\qquad -a_0^3 b_3^3 $
$\quad +(-3 a_3^2 b_0^3+2 a_2 a_3 b_0^2 b_1-2 a_1 a_3 b_0 b_1^2+2 a_0 a_3 b_1^3-a_2^2 b_0^2 b_2+4 a_1 a_3 b_0^2 b_2 $
$\qquad +a_1 a_2 b_0 b_1 b_2-6 a_0 a_3 b_0 b_1 b_2-a_0 a_2 b_1^2 b_2-a_1^2 b_0 b_2^2+2 a_0 a_2 b_0 b_2^2+a_0 a_1 b_1 b_2^2 $
$\qquad -a_0^2 b_2^3-3 a_1 a_2 b_0^2 b_3+6 a_0 a_3 b_0^2 b_3+2 a_1^2 b_0 b_1 b_3+a_0 a_2 b_0 b_1 b_3-2 a_0 a_1 b_1^2 b_3 $
$\qquad -a_0 a_1 b_0 b_2 b_3+3 a_0^2 b_1 b_2 b_3-3 a_0^2 b_0 b_3^2)x $
$\quad +(a_2^3 b_0^2-3 a_1 a_2 a_3 b_0^2+3 a_0 a_3^2 b_0^2-a_1 a_2^2 b_0 b_1+2 a_1^2 a_3 b_0 b_1+a_0 a_2 a_3 b_0 b_1+a_0 a_2^2 b_1^2 $
$\qquad -2 a_0 a_1 a_3 b_1^2+a_1^2 a_2 b_0 b_2-2 a_0 a_2^2 b_0 b_2-a_0 a_1 a_3 b_0 b_2-a_0 a_1 a_2 b_1 b_2+3 a_0^2 a_3 b_1 b_2 $
$\qquad +a_0^2 a_2 b_2^2-2 a_1^3 b_0 b_3+6 a_0 a_1 a_2 b_0 b_3-6 a_0^2 a_3 b_0 b_3+2 a_0 a_1^2 b_1 b_3-4 a_0^2 a_2 b_1 b_3 $
$\qquad -2 a_0^2 a_1 b_2 b_3+3 a_0^3 b_3^2)y $
$\quad +(3 a_3 b_0^3-a_2 b_0^2 b_1+a_1 b_0 b_1^2-a_0 b_1^3-2 a_1 b_0^2 b_2+3 a_0 b_0 b_1 b_2-3 a_0 b_0^2 b_3)x^2 $
$\quad +(3 a_1 a_2 b_0^2-6 a_0 a_3 b_0^2-2 a_1^2 b_0 b_1-a_0 a_2 b_0 b_1+2 a_0 a_1 b_1^2+a_0 a_1 b_0 b_2-3 a_0^2 b_1 b_2 $
$\qquad +6 a_0^2 b_0 b_3)x y $
$\quad +(a_1^3 b_0-3 a_0 a_1 a_2 b_0+3 a_0^2 a_3 b_0-a_0 a_1^2 b_1+2 a_0^2 a_2 b_1+a_0^2 a_1 b_2-3 a_0^3 b_3)y^2 $
$\quad -b_0^3x^3 +3 a_0 b_0^2 x^2 y -3 a_0^2 b_0 x y^2 +a_0^3 y^3 \quad =0 $
曲線形状によりベジェ曲線の次数が低下し2次曲線、すなわち $a_0=0$、$b_0=0$ である場合、陰関数の左辺が $0$ になり、根を求めることができない。この場合は2次用の陰関数表示を用いる。
- 曲線 ${\boldsymbol{B}}_0$ が2次の場合の陰関数表示:
$F_0(x,y)=a_3^2 b_1^2-a_2 a_3 b_1 b_2+a_1 a_3 b_2^2+a_2^2 b_1 b_3-2 a_1 a_3 b_1 b_3-a_1 a_2 b_2 b_3+a_1^2 b_3^2$
$ \quad +(-2 a_3 b_1^2+a_2 b_1 b_2-a_1 b_2^2+2 a_1 b_1 b_3) x
+(-a_2^2 b_1+2 a_1 a_3 b_1+a_1 a_2 b_2-2 a_1^2 b_3) y$
$ \quad +b_1^2 x^2-2 a_1 b_1 x y+a_1^2 y^2 \quad =0$
さらに、曲線が1次(直線)、すなわち $a_0=0$、$a_1=0$、$b_0=0$、$b_1=0$ である場合は、1次用の陰関数表示を用いる。
- 曲線 ${\boldsymbol{B}}_0$ が1次の場合の陰関数表示:
$F_0(x,y)=-a_3 b_2+a_2 b_3+b_2 x-a_2 y \quad =0$
曲線 ${\boldsymbol{B}}_0$ の陰関数 $F_0(x,y)=0$ に、曲線 ${\boldsymbol{B}}_1$ のパラメトリック関数 $x=f_1(u)$ と $y=g_1(u)$ を代入することで、$u$ をパラメータとする陰伏方程式 $F_0(u)=0$ を得る。これの実根の $u$ が交点候補のパラメータである。
陰伏方程式 $F_0(u)=0$ の各項の係数を求める式をSage Math(Notebook:Appendix B)で求めた。
- ${\boldsymbol{B}}_0$ が3次の場合の陰伏方程式 $F_0(u)=0$(9次の代数方程式)の各項の係数:
| 項 | 係数 |
|---|---|
| $u^9$ | $-b_0^3 c_0^3+3 a_0 b_0^2 c_0^2 d_0-3 a_0^2 b_0 c_0 d_0^2+a_0^3 d_0^3$ |
| $u^8$ | $-3 b_0^3 c_0^2 c_1+6 a_0 b_0^2 c_0 c_1 d_0-3 a_0^2 b_0 c_1 d_0^2+3 (a_0 b_0^2 c_0^2-2 a_0^2 b_0 c_0 d_0$$+a_0^3 d_0^2) d_1$ |
| $u^7$ | $-3 b_0^3 c_0 c_1^2-3 b_0^3 c_0^2 c_2-3 a_0^2 b_0 c_2 d_0^2-3 (a_0^2 b_0 c_0-a_0^3 d_0) d_1^2+3 (a_0 b_0^2 c_1^2$$+2 a_0 b_0^2 c_0 c_2) d_0+6 (a_0 b_0^2 c_0 c_1-a_0^2 b_0 c_1 d_0) d_1+3 (a_0 b_0^2 c_0^2-2 a_0^2 b_0 c_0 d_0$$+a_0^3 d_0^2) d_2$ |
| $u^6$ | $-b_0^3 c_1^3-6 b_0^3 c_0 c_1 c_2-3 b_0^3 c_0^2 c_3-3 a_0^2 b_0 c_1 d_1^2+a_0^3 d_1^3+(3 a_3 b_0^3-a_2 b_0^2 b_1$$+a_1 b_0 b_1^2-a_0 b_1^3-3 a_0 b_0^2 b_3-(2 a_1 b_0^2-3 a_0 b_0 b_1) b_2) c_0^2+(a_0^2 a_1 b_2$$-3 a_0^3 b_3-3 a_0^2 b_0 c_3+(a_1^3-3 a_0 a_1 a_2+3 a_0^2 a_3) b_0-(a_0 a_1^2-2 a_0^2 a_2) b_1) d_0^2$$+(6 a_0 b_0^2 c_1 c_2+6 a_0 b_0^2 c_0 c_3+(2 a_0 a_1 b_1^2+6 a_0^2 b_0 b_3+3 (a_1 a_2-2 a_0 a_3) b_0^2$$-(2 a_1^2+a_0 a_2) b_0 b_1+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) c_0) d_0+3 (a_0 b_0^2 c_1^2$$+2 a_0 b_0^2 c_0 c_2-2 a_0^2 b_0 c_2 d_0) d_1+6 (a_0 b_0^2 c_0 c_1-a_0^2 b_0 c_1 d_0-(a_0^2 b_0 c_0$$-a_0^3 d_0) d_1) d_2+3 (a_0 b_0^2 c_0^2-2 a_0^2 b_0 c_0 d_0+a_0^3 d_0^2) d_3$ |
| $u^5$ | $-3 b_0^3 c_1^2 c_2-3 b_0^3 c_0 c_2^2-6 b_0^3 c_0 c_1 c_3-3 a_0^2 b_0 c_2 d_1^2+2 (3 a_3 b_0^3-a_2 b_0^2 b_1$$+a_1 b_0 b_1^2-a_0 b_1^3-3 a_0 b_0^2 b_3-(2 a_1 b_0^2-3 a_0 b_0 b_1) b_2) c_0 c_1-3 (a_0^2 b_0 c_0$$-a_0^3 d_0) d_2^2+(3 a_0 b_0^2 c_2^2+6 a_0 b_0^2 c_1 c_3+(2 a_0 a_1 b_1^2+6 a_0^2 b_0 b_3+3 (a_1 a_2$$-2 a_0 a_3) b_0^2-(2 a_1^2+a_0 a_2) b_0 b_1+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) c_1) d_0$$+(6 a_0 b_0^2 c_1 c_2+6 a_0 b_0^2 c_0 c_3+(2 a_0 a_1 b_1^2+6 a_0^2 b_0 b_3+3 (a_1 a_2-2 a_0 a_3) b_0^2$$-(2 a_1^2+a_0 a_2) b_0 b_1+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) c_0+2 (a_0^2 a_1 b_2-3 a_0^3 b_3$$-3 a_0^2 b_0 c_3+(a_1^3-3 a_0 a_1 a_2+3 a_0^2 a_3) b_0-(a_0 a_1^2-2 a_0^2 a_2) b_1) d_0) d_1$$+3 (a_0 b_0^2 c_1^2+2 a_0 b_0^2 c_0 c_2-2 a_0^2 b_0 c_2 d_0-2 a_0^2 b_0 c_1 d_1+a_0^3 d_1^2) d_2$$+6 (a_0 b_0^2 c_0 c_1-a_0^2 b_0 c_1 d_0-(a_0^2 b_0 c_0-a_0^3 d_0) d_1) d_3$ |
| $u^4$ | $-3 b_0^3 c_1 c_2^2+(3 a_3 b_0^3-a_2 b_0^2 b_1+a_1 b_0 b_1^2-a_0 b_1^3-3 a_0 b_0^2 b_3-(2 a_1 b_0^2$$-3 a_0 b_0 b_1) b_2) c_1^2+2 (3 a_3 b_0^3-a_2 b_0^2 b_1+a_1 b_0 b_1^2-a_0 b_1^3-3 a_0 b_0^2 b_3$$-(2 a_1 b_0^2-3 a_0 b_0 b_1) b_2) c_0 c_2+(a_0^2 a_1 b_2-3 a_0^3 b_3-3 a_0^2 b_0 c_3+(a_1^3$$-3 a_0 a_1 a_2+3 a_0^2 a_3) b_0-(a_0 a_1^2-2 a_0^2 a_2) b_1) d_1^2-3 (a_0^2 b_0 c_1-a_0^3 d_1) d_2^2$$-3 (b_0^3 c_1^2+2 b_0^3 c_0 c_2) c_3+(6 a_0 b_0^2 c_2 c_3+(2 a_0 a_1 b_1^2+6 a_0^2 b_0 b_3+3 (a_1 a_2$$-2 a_0 a_3) b_0^2-(2 a_1^2+a_0 a_2) b_0 b_1+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) c_2) d_0+(3 a_0 b_0^2 c_2^2$$+6 a_0 b_0^2 c_1 c_3+(2 a_0 a_1 b_1^2+6 a_0^2 b_0 b_3+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2$$+a_0 a_2) b_0 b_1+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) c_1) d_1+(6 a_0 b_0^2 c_1 c_2+6 a_0 b_0^2 c_0 c_3$$-6 a_0^2 b_0 c_2 d_1+(2 a_0 a_1 b_1^2+6 a_0^2 b_0 b_3+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2$$+a_0 a_2) b_0 b_1+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) c_0+2 (a_0^2 a_1 b_2-3 a_0^3 b_3-3 a_0^2 b_0 c_3$$+(a_1^3-3 a_0 a_1 a_2+3 a_0^2 a_3) b_0-(a_0 a_1^2-2 a_0^2 a_2) b_1) d_0) d_2+3 (a_0 b_0^2 c_1^2$$+2 a_0 b_0^2 c_0 c_2-2 a_0^2 b_0 c_2 d_0-2 a_0^2 b_0 c_1 d_1+a_0^3 d_1^2-2 (a_0^2 b_0 c_0-a_0^3 d_0) d_2) d_3$ |
| $u^3$ | $-b_0^3 c_2^3-3 b_0^3 c_0 c_3^2-3 a_0^2 b_0 c_2 d_2^2+a_0^3 d_2^3+2 (3 a_3 b_0^3-a_2 b_0^2 b_1+a_1 b_0 b_1^2$$-a_0 b_1^3-3 a_0 b_0^2 b_3-(2 a_1 b_0^2-3 a_0 b_0 b_1) b_2) c_1 c_2-3 (a_0^2 b_0 c_0-a_0^3 d_0) d_3^2$$-(3 a_3^2 b_0^3-2 a_2 a_3 b_0^2 b_1+2 a_1 a_3 b_0 b_1^2-2 a_0 a_3 b_1^3+a_0^2 b_2^3+3 a_0^2 b_0 b_3^2$$-(a_0 a_1 b_1-(a_1^2-2 a_0 a_2) b_0) b_2^2+(a_0 a_2 b_1^2+(a_2^2-4 a_1 a_3) b_0^2-(a_1 a_2$$-6 a_0 a_3) b_0 b_1) b_2+(2 a_0 a_1 b_1^2+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2+a_0 a_2) b_0 b_1$$+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) b_3) c_0-2 (3 b_0^3 c_1 c_2-(3 a_3 b_0^3-a_2 b_0^2 b_1+a_1 b_0 b_1^2$$-a_0 b_1^3-3 a_0 b_0^2 b_3-(2 a_1 b_0^2-3 a_0 b_0 b_1) b_2) c_0) c_3+(a_0^2 a_2 b_2^2+3 a_0^3 b_3^2$$+3 a_0 b_0^2 c_3^2+(a_2^3-3 a_1 a_2 a_3+3 a_0 a_3^2) b_0^2-(a_1 a_2^2-(2 a_1^2+a_0 a_2) a_3) b_0 b_1$$+(a_0 a_2^2-2 a_0 a_1 a_3) b_1^2+((a_1^2 a_2-2 a_0 a_2^2-a_0 a_1 a_3) b_0-(a_0 a_1 a_2$$-3 a_0^2 a_3) b_1) b_2-2 (a_0^2 a_1 b_2+(a_1^3-3 a_0 a_1 a_2+3 a_0^2 a_3) b_0-(a_0 a_1^2$$-2 a_0^2 a_2) b_1) b_3+(2 a_0 a_1 b_1^2+6 a_0^2 b_0 b_3+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2$$+a_0 a_2) b_0 b_1+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) c_3) d_0+(6 a_0 b_0^2 c_2 c_3+(2 a_0 a_1 b_1^2$$+6 a_0^2 b_0 b_3+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2+a_0 a_2) b_0 b_1+(a_0 a_1 b_0$$-3 a_0^2 b_1) b_2) c_2) d_1+(3 a_0 b_0^2 c_2^2+6 a_0 b_0^2 c_1 c_3+(2 a_0 a_1 b_1^2+6 a_0^2 b_0 b_3$$+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2+a_0 a_2) b_0 b_1+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) c_1$$+2 (a_0^2 a_1 b_2-3 a_0^3 b_3-3 a_0^2 b_0 c_3+(a_1^3-3 a_0 a_1 a_2+3 a_0^2 a_3) b_0-(a_0 a_1^2$$-2 a_0^2 a_2) b_1) d_1) d_2+(6 a_0 b_0^2 c_1 c_2+6 a_0 b_0^2 c_0 c_3-6 a_0^2 b_0 c_2 d_1+(2 a_0 a_1 b_1^2$$+6 a_0^2 b_0 b_3+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2+a_0 a_2) b_0 b_1+(a_0 a_1 b_0$$-3 a_0^2 b_1) b_2) c_0+2 (a_0^2 a_1 b_2-3 a_0^3 b_3-3 a_0^2 b_0 c_3+(a_1^3-3 a_0 a_1 a_2$$+3 a_0^2 a_3) b_0-(a_0 a_1^2-2 a_0^2 a_2) b_1) d_0-6 (a_0^2 b_0 c_1-a_0^3 d_1) d_2) d_3$ |
| $u^2$ | $-3 b_0^3 c_1 c_3^2+(3 a_3 b_0^3-a_2 b_0^2 b_1+a_1 b_0 b_1^2-a_0 b_1^3-3 a_0 b_0^2 b_3-(2 a_1 b_0^2$$-3 a_0 b_0 b_1) b_2) c_2^2+(a_0^2 a_1 b_2-3 a_0^3 b_3-3 a_0^2 b_0 c_3+(a_1^3-3 a_0 a_1 a_2$$+3 a_0^2 a_3) b_0-(a_0 a_1^2-2 a_0^2 a_2) b_1) d_2^2-3 (a_0^2 b_0 c_1-a_0^3 d_1) d_3^2-(3 a_3^2 b_0^3$$-2 a_2 a_3 b_0^2 b_1+2 a_1 a_3 b_0 b_1^2-2 a_0 a_3 b_1^3+a_0^2 b_2^3+3 a_0^2 b_0 b_3^2-(a_0 a_1 b_1-(a_1^2$$-2 a_0 a_2) b_0) b_2^2+(a_0 a_2 b_1^2+(a_2^2-4 a_1 a_3) b_0^2-(a_1 a_2-6 a_0 a_3) b_0 b_1) b_2$$+(2 a_0 a_1 b_1^2+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2+a_0 a_2) b_0 b_1+(a_0 a_1 b_0$$-3 a_0^2 b_1) b_2) b_3) c_1-(3 b_0^3 c_2^2-2 (3 a_3 b_0^3-a_2 b_0^2 b_1+a_1 b_0 b_1^2-a_0 b_1^3$$-3 a_0 b_0^2 b_3-(2 a_1 b_0^2-3 a_0 b_0 b_1) b_2) c_1) c_3+(a_0^2 a_2 b_2^2+3 a_0^3 b_3^2+3 a_0 b_0^2 c_3^2$$+(a_2^3-3 a_1 a_2 a_3+3 a_0 a_3^2) b_0^2-(a_1 a_2^2-(2 a_1^2+a_0 a_2) a_3) b_0 b_1+(a_0 a_2^2$$-2 a_0 a_1 a_3) b_1^2+((a_1^2 a_2-2 a_0 a_2^2-a_0 a_1 a_3) b_0-(a_0 a_1 a_2-3 a_0^2 a_3) b_1) b_2$$-2 (a_0^2 a_1 b_2+(a_1^3-3 a_0 a_1 a_2+3 a_0^2 a_3) b_0-(a_0 a_1^2-2 a_0^2 a_2) b_1) b_3$$+(2 a_0 a_1 b_1^2+6 a_0^2 b_0 b_3+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2+a_0 a_2) b_0 b_1$$+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) c_3) d_1+(6 a_0 b_0^2 c_2 c_3+(2 a_0 a_1 b_1^2+6 a_0^2 b_0 b_3$$+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2+a_0 a_2) b_0 b_1+(a_0 a_1 b_0$$-3 a_0^2 b_1) b_2) c_2) d_2+(3 a_0 b_0^2 c_2^2+6 a_0 b_0^2 c_1 c_3-6 a_0^2 b_0 c_2 d_2+3 a_0^3 d_2^2$$+(2 a_0 a_1 b_1^2+6 a_0^2 b_0 b_3+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2+a_0 a_2) b_0 b_1$$+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) c_1+2 (a_0^2 a_1 b_2-3 a_0^3 b_3-3 a_0^2 b_0 c_3+(a_1^3$$-3 a_0 a_1 a_2+3 a_0^2 a_3) b_0-(a_0 a_1^2-2 a_0^2 a_2) b_1) d_1) d_3$ |
| $u$ | $-3 b_0^3 c_2 c_3^2+2 (3 a_3 b_0^3-a_2 b_0^2 b_1+a_1 b_0 b_1^2-a_0 b_1^3-3 a_0 b_0^2 b_3-(2 a_1 b_0^2$$-3 a_0 b_0 b_1) b_2) c_2 c_3-3 (a_0^2 b_0 c_2-a_0^3 d_2) d_3^2-(3 a_3^2 b_0^3-2 a_2 a_3 b_0^2 b_1$$+2 a_1 a_3 b_0 b_1^2-2 a_0 a_3 b_1^3+a_0^2 b_2^3+3 a_0^2 b_0 b_3^2-(a_0 a_1 b_1-(a_1^2$$-2 a_0 a_2) b_0) b_2^2+(a_0 a_2 b_1^2+(a_2^2-4 a_1 a_3) b_0^2-(a_1 a_2-6 a_0 a_3) b_0 b_1) b_2$$+(2 a_0 a_1 b_1^2+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2+a_0 a_2) b_0 b_1+(a_0 a_1 b_0$$-3 a_0^2 b_1) b_2) b_3) c_2+(a_0^2 a_2 b_2^2+3 a_0^3 b_3^2+3 a_0 b_0^2 c_3^2+(a_2^3-3 a_1 a_2 a_3$$+3 a_0 a_3^2) b_0^2-(a_1 a_2^2-(2 a_1^2+a_0 a_2) a_3) b_0 b_1+(a_0 a_2^2-2 a_0 a_1 a_3) b_1^2$$+((a_1^2 a_2-2 a_0 a_2^2-a_0 a_1 a_3) b_0-(a_0 a_1 a_2-3 a_0^2 a_3) b_1) b_2-2 (a_0^2 a_1 b_2$$+(a_1^3-3 a_0 a_1 a_2+3 a_0^2 a_3) b_0-(a_0 a_1^2-2 a_0^2 a_2) b_1) b_3+(2 a_0 a_1 b_1^2$$+6 a_0^2 b_0 b_3+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2+a_0 a_2) b_0 b_1+(a_0 a_1 b_0$$-3 a_0^2 b_1) b_2) c_3) d_2+(6 a_0 b_0^2 c_2 c_3+(2 a_0 a_1 b_1^2+6 a_0^2 b_0 b_3+3 (a_1 a_2$$-2 a_0 a_3) b_0^2-(2 a_1^2+a_0 a_2) b_0 b_1+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) c_2+2 (a_0^2 a_1 b_2$$-3 a_0^3 b_3-3 a_0^2 b_0 c_3+(a_1^3-3 a_0 a_1 a_2+3 a_0^2 a_3) b_0-(a_0 a_1^2$$-2 a_0^2 a_2) b_1) d_2) d_3$ |
| $1$ | $a_3^3 b_0^3-a_2 a_3^2 b_0^2 b_1+a_1 a_3^2 b_0 b_1^2-a_0 a_3^2 b_1^3+a_0^2 a_3 b_2^3-a_0^3 b_3^3-b_0^3 c_3^3$$+a_0^3 d_3^3-(a_0 a_1 a_3 b_1-(a_1^2-2 a_0 a_2) a_3 b_0) b_2^2+(a_0^2 a_1 b_2+(a_1^3$$-3 a_0 a_1 a_2+3 a_0^2 a_3) b_0-(a_0 a_1^2-2 a_0^2 a_2) b_1) b_3^2+(3 a_3 b_0^3-a_2 b_0^2 b_1$$+a_1 b_0 b_1^2-a_0 b_1^3-3 a_0 b_0^2 b_3-(2 a_1 b_0^2-3 a_0 b_0 b_1) b_2) c_3^2+(a_0^2 a_1 b_2$$-3 a_0^3 b_3-3 a_0^2 b_0 c_3+(a_1^3-3 a_0 a_1 a_2+3 a_0^2 a_3) b_0-(a_0 a_1^2-2 a_0^2 a_2) b_1) d_3^2$$+(a_0 a_2 a_3 b_1^2+(a_2^2 a_3-2 a_1 a_3^2) b_0^2-(a_1 a_2 a_3-3 a_0 a_3^2) b_0 b_1) b_2-(a_0^2 a_2 b_2^2$$+(a_2^3-3 a_1 a_2 a_3+3 a_0 a_3^2) b_0^2-(a_1 a_2^2-(2 a_1^2+a_0 a_2) a_3) b_0 b_1+(a_0 a_2^2$$-2 a_0 a_1 a_3) b_1^2+((a_1^2 a_2-2 a_0 a_2^2-a_0 a_1 a_3) b_0-(a_0 a_1 a_2$$-3 a_0^2 a_3) b_1) b_2) b_3-(3 a_3^2 b_0^3-2 a_2 a_3 b_0^2 b_1+2 a_1 a_3 b_0 b_1^2-2 a_0 a_3 b_1^3$$+a_0^2 b_2^3+3 a_0^2 b_0 b_3^2-(a_0 a_1 b_1-(a_1^2-2 a_0 a_2) b_0) b_2^2+(a_0 a_2 b_1^2+(a_2^2$$-4 a_1 a_3) b_0^2-(a_1 a_2-6 a_0 a_3) b_0 b_1) b_2+(2 a_0 a_1 b_1^2+3 (a_1 a_2-2 a_0 a_3) b_0^2$$-(2 a_1^2+a_0 a_2) b_0 b_1+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) b_3) c_3+(a_0^2 a_2 b_2^2+3 a_0^3 b_3^2$$+3 a_0 b_0^2 c_3^2+(a_2^3-3 a_1 a_2 a_3+3 a_0 a_3^2) b_0^2-(a_1 a_2^2-(2 a_1^2+a_0 a_2) a_3) b_0 b_1$$+(a_0 a_2^2-2 a_0 a_1 a_3) b_1^2+((a_1^2 a_2-2 a_0 a_2^2-a_0 a_1 a_3) b_0-(a_0 a_1 a_2$$-3 a_0^2 a_3) b_1) b_2-2 (a_0^2 a_1 b_2+(a_1^3-3 a_0 a_1 a_2+3 a_0^2 a_3) b_0-(a_0 a_1^2$$-2 a_0^2 a_2) b_1) b_3+(2 a_0 a_1 b_1^2+6 a_0^2 b_0 b_3+3 (a_1 a_2-2 a_0 a_3) b_0^2-(2 a_1^2$$+a_0 a_2) b_0 b_1+(a_0 a_1 b_0-3 a_0^2 b_1) b_2) c_3) d_3$ |
- ${\boldsymbol{B}}_0$ が2次の場合の陰伏方程式 $F_0(u)=0$(6次の代数方程式)の各項の係数:
| 項 | 係数 |
|---|---|
| $u^6$ | $b_1^2 c_0^2-2 a_1 b_1 c_0 d_0+a_1^2 d_0^2$ |
| $u^5$ | $2 b_1^2 c_0 c_1-2 a_1 b_1 c_1 d_0-2 (a_1 b_1 c_0-a_1^2 d_0) d_1$ |
| $u^4$ | $b_1^2 c_1^2+2 b_1^2 c_0 c_2-2 a_1 b_1 c_2 d_0-2 a_1 b_1 c_1 d_1+a_1^2 d_1^2-2 (a_1 b_1 c_0-a_1^2 d_0) d_2$ |
| $u^3$ | $2 b_1^2 c_1 c_2+2 b_1^2 c_0 c_3-2 a_1 b_1 c_2 d_1-(2 a_3 b_1^2-a_2 b_1 b_2+a_1 b_2^2-2 a_1 b_1 b_3) c_0$$+(a_1 a_2 b_2-2 a_1^2 b_3-2 a_1 b_1 c_3-(a_2^2-2 a_1 a_3) b_1) d_0-2 (a_1 b_1 c_1$$-a_1^2 d_1) d_2-2 (a_1 b_1 c_0-a_1^2 d_0) d_3$ |
| $u^2$ | $b_1^2 c_2^2+2 b_1^2 c_1 c_3-2 a_1 b_1 c_2 d_2+a_1^2 d_2^2-(2 a_3 b_1^2-a_2 b_1 b_2+a_1 b_2^2$$-2 a_1 b_1 b_3) c_1+(a_1 a_2 b_2-2 a_1^2 b_3-2 a_1 b_1 c_3-(a_2^2-2 a_1 a_3) b_1) d_1$$-2 (a_1 b_1 c_1-a_1^2 d_1) d_3$ |
| $u$ | $2 b_1^2 c_2 c_3-(2 a_3 b_1^2-a_2 b_1 b_2+a_1 b_2^2-2 a_1 b_1 b_3) c_2+(a_1 a_2 b_2-2 a_1^2 b_3$$-2 a_1 b_1 c_3-(a_2^2-2 a_1 a_3) b_1) d_2-2 (a_1 b_1 c_2-a_1^2 d_2) d_3$ |
| $1$ | $a_3^2 b_1^2-a_2 a_3 b_1 b_2+a_1 a_3 b_2^2+a_1^2 b_3^2+b_1^2 c_3^2+a_1^2 d_3^2-(a_1 a_2 b_2-(a_2^2$$-2 a_1 a_3) b_1) b_3-(2 a_3 b_1^2-a_2 b_1 b_2+a_1 b_2^2-2 a_1 b_1 b_3) c_3+(a_1 a_2 b_2$$-2 a_1^2 b_3-2 a_1 b_1 c_3-(a_2^2-2 a_1 a_3) b_1) d_3$ |
- ${\boldsymbol{B}}_0$ が1次の場合の陰伏方程式 $F_0(u)=0$(3次の代数方程式)の各項の係数:
| 項 | 係数 |
|---|---|
| $u^3$ | $b_2 c_0-a_2 d_0$ |
| $u^2$ | $b_2 c_1-a_2 d_1$ |
| $u$ | $b_2 c_2-a_2 d_2$ |
| $1$ | $-a_3 b_2+a_2 b_3+b_2 c_3-a_2 d_3$ |
実根の分離
ブダン・フーリエの定理によるふるい分け
ベジェ曲線の交点検出の実用的な応用では、大半のベジェ曲線には交点が含まれないか、含まれても1点だけで、2点以上の交点が含まれるものはきわめて少ないと想定される。そのため、ふるい分けにより平均処理量が大幅に低減される効果があると期待される。
ふるい分けには計算量の少ないブダン・フーリエの定理を用いる。方程式 $p(x)=0$ についてのブダン・フーリエの定理は、以下の2つの命題がある。[9]
- 変数を変換した変換多項式について、各次数の係数の符号変化の数の差($p(x+a)$ と $p(x+b)$ の係数の符号変化の数の差)を用いるブダンの命題
- 導関数列の符号変化の数の差($x=a$ における $\lbrace p(a), p^{(1)}(a), p^{(2)}(a), \dots, p^{(9)}(a) \rbrace$ の符号変化の数と、$x=b$ における $\lbrace p(b), p^{(1)}(b), p^{(2)}(b), \dots, p^{(9)}(b) \rbrace$ の符号変化の数の差)を用いるフーリエの命題
今回は机上検証では両者について計算して結果が一致することを確認し、試行実装では設計が容易な前者を用いた。
ベジェ曲線全体を対象とするため、区間 $(0,1)$ に含まれる実根の数が以下のいずれであるかを判定し、以降の処理を決定する。
- 実根がない → 交差なし
- 実根が1個ある → 区間全体を分離区間とし、反復的な求根法を行う
- その他 → ヴァンサンの定理による実根分離を行う
多項式
$\quad p(x)=e_0 x^9+e_1 x^8+e_2 x^7+e_3 x^6+e_4 x^5+e_5 x^4+e_6 x^3+e_7 x^2+e_8 x+e_9$
に対し、$b=1$ の変換多項式は;
$\quad p(x+1)=e_0 (x+1)^9+e_1 (x+1)^8+e_2 (x+1)^7+e_3 (x+1)^6+e_4 (x+1)^5$
$\quad \qquad \qquad +e_5 (x+1)^4+e_6 (x+1)^3+e_7 (x+1)^2+e_8 (x+1)+e_9$
である。各次数の係数は、Sage Math(Notebook:Appendix C)で式展開した以下を用いて求めた。
| 項 | 係数 |
|---|---|
| $x^9$ | $e_0$ |
| $x^8$ | $9 e_0+e_1$ |
| $x^7$ | $36 e_0+8 e_1+e_2$ |
| $x^6$ | $84 e_0+28 e_1+7 e_2+e_3$ |
| $x^5$ | $126 e_0+56 e_1+21 e_2+6 e_3+e_4$ |
| $x^4$ | $126 e_0+70 e_1+35 e_2+15 e_3+5 e_4+e_5$ |
| $x^3$ | $84 e_0+56 e_1+35 e_2+20 e_3+10 e_4+4 e_5+e_6$ |
| $x^2$ | $36 e_0+28 e_1+21 e_2+15 e_3+10 e_4+6 e_5+3 e_6+e_7$ |
| $x$ | $9 e_0+8 e_1+7 e_2+6 e_3+5 e_4+4 e_5+3 e_6+2 e_7+e_8$ |
| $1$ | $e_0+e_1+e_2+e_3+e_4+e_5+e_6+e_7+e_8+e_9$ |
ヴァンサンの定理による実根分離
ヴァンサンの定理の応用手法であるVAG法(Vincent–Alesina–Galuzzi)を用いて、実根が1個含まれる区間を求める。[9]
区間 $(a, b)$ について、$p(x)$ の変換多項式
f(x) = (x+1)^{deg(p)} p \left (\frac{a+bx}{1+x} \right )
の係数列の符号変化の数を求める。
- 0であれば実根なし →区間 $(a, b)$ は棄却
- 1であれば実根が1個ある →区間 $(a, b)$ を実根が1個含まれる分離区間として出力
- 2以上であれば実根が1個以上ある →区間 $(a, b)$ を中点 $m$ で2分割し、区間 $(a, m)$ と区間 $(m, b)$ それぞれにVAG法を再帰適用
なお、初期値はベジェ曲線全体を対象とするため $a=0$、$b=1$ とする。
以下のチャートは、冒頭の例3の陰伏方程式 $F_0(u)=0$ を、VAG法により区間分割を反復して実根分離した例である。赤枠は実根がないので棄却、青枠は実根1個で分離完了した区間である。

多項式
$\quad p(x)=e_0 x^9+e_1 x^8+e_2 x^7+e_3 x^6+e_4 x^5+e_5 x^4+e_6 x^3+e_7 x^2+e_8 x+e_9$
に対する変換多項式 $f(x)$ の各次数の係数は、Sage Math(Notebook:Appendix D)で式展開した以下を用いて求めた。
| 項 | 係数 |
|---|---|
| $x^9$ | $e_0 b^9+e_1 b^8+e_2 b^7+e_3 b^6+e_4 b^5+e_5 b^4+e_6 b^3+e_7 b^2+e_8 b+e_9$ |
| $x^8$ | $9 a e_0+e_1) b^8+2 (4 a e_1+e_2) b^7+(7 a e_2+3 e_3) b^6+2 (3 a e_3+2 e_4) b^5$$+5 (a e_4+e_5) b^4+2 (2 a e_5+3 e_6) b^3+(3 a e_6+7 e_7) b^2+a e_8+2 (a e_7$$+4 e_8) b+9 e_9$ |
| $x^7$ | $(36 a^2 e_0+8 a e_1+e_2) b^7+(28 a^2 e_1+14 a e_2+3 e_3) b^6+3 (7 a^2 e_2$$+6 a e_3+2 e_4) b^5+5 (3 a^2 e_3+4 a e_4+2 e_5) b^4+5 (2 a^2 e_4+4 a e_5$$+3 e_6) b^3+a^2 e_7+3 (2 a^2 e_5+6 a e_6+7 e_7) b^2+8 a e_8+(3 a^2 e_6+14 a e_7$$+28 e_8) b+36 e_9$ |
| $x^6$ | $(84 a^3 e_0+28 a^2 e_1+7 a e_2+e_3) b^6+2 (28 a^3 e_1+21 a^2 e_2+9 a e_3$$+2 e_4) b^5+5 (7 a^3 e_2+9 a^2 e_3+6 a e_4+2 e_5) b^4+a^3 e_6+20 (a^3 e_3$$+2 a^2 e_4+2 a e_5+e_6) b^3+7 a^2 e_7+5 (2 a^3 e_4+6 a^2 e_5+9 a e_6+7 e_7) b^2$$+28 a e_8+2 (2 a^3 e_5+9 a^2 e_6+21 a e_7+28 e_8) b+84 e_9$ |
| $x^5$ | $(126 a^4 e_0+56 a^3 e_1+21 a^2 e_2+6 a e_3+e_4) b^5+a^4 e_5+5 (14 a^4 e_1$$+14 a^3 e_2+9 a^2 e_3+4 a e_4+e_5) b^4+6 a^3 e_6+5 (7 a^4 e_2+12 a^3 e_3$$+12 a^2 e_4+8 a e_5+3 e_6) b^3+21 a^2 e_7+5 (3 a^4 e_3+8 a^3 e_4+12 a^2 e_5$$+12 a e_6+7 e_7) b^2+56 a e_8+5 (a^4 e_4+4 a^3 e_5+9 a^2 e_6+14 a e_7$$+14 e_8) b+126 e_9$ |
| $x^4$ | $a^5 e_4+5 a^4 e_5+(126 a^5 e_0+70 a^4 e_1+35 a^3 e_2+15 a^2 e_3+5 a e_4+e_5) b^4$$+15 a^3 e_6+2 (28 a^5 e_1+35 a^4 e_2+30 a^3 e_3+20 a^2 e_4+10 a e_5+3 e_6) b^3$$+35 a^2 e_7+3 (7 a^5 e_2+15 a^4 e_3+20 a^3 e_4+20 a^2 e_5+15 a e_6+7 e_7) b^2$$+70 a e_8+2 (3 a^5 e_3+10 a^4 e_4+20 a^3 e_5+30 a^2 e_6+35 a e_7+28 e_8) b$$+126 e_9$ |
| $x^3$ | $a^6 e_3+4 a^5 e_4+10 a^4 e_5+20 a^3 e_6+(84 a^6 e_0+56 a^5 e_1+35 a^4 e_2$$+20 a^3 e_3+10 a^2 e_4+4 a e_5+e_6) b^3+35 a^2 e_7+(28 a^6 e_1+42 a^5 e_2$$+45 a^4 e_3+40 a^3 e_4+30 a^2 e_5+18 a e_6+7 e_7) b^2+56 a e_8+(7 a^6 e_2$$+18 a^5 e_3+30 a^4 e_4+40 a^3 e_5+45 a^2 e_6+42 a e_7+28 e_8) b+84 e_9$ |
| $x^2$ | $a^7 e_2+3 a^6 e_3+6 a^5 e_4+10 a^4 e_5+15 a^3 e_6+21 a^2 e_7+(36 a^7 e_0$$+28 a^6 e_1+21 a^5 e_2+15 a^4 e_3+10 a^3 e_4+6 a^2 e_5+3 a e_6+e_7) b^2$$+28 a e_8+2 (4 a^7 e_1+7 a^6 e_2+9 a^5 e_3+10 a^4 e_4+10 a^3 e_5+9 a^2 e_6$$+7 a e_7+4 e_8) b+36 e_9$ |
| $x$ | $a^8 e_1+2 a^7 e_2+3 a^6 e_3+4 a^5 e_4+5 a^4 e_5+6 a^3 e_6+7 a^2 e_7+8 a e_8$$+(9 a^8 e_0+8 a^7 e_1+7 a^6 e_2+6 a^5 e_3+5 a^4 e_4+4 a^3 e_5+3 a^2 e_6+2 a e_7$$+e_8) b+9 e_9$ |
| $1$ | $a^9 e_0+a^8 e_1+a^7 e_2+a^6 e_3+a^5 e_4+a^4 e_5+a^3 e_6+a^2 e_7+a e_8+e_9$ |
反復的な求根法
二分法による区間の縮小
区間内に極小値や極大値などの特異点が含まれる場合に、収束性が著しく悪化したり、ニュートン・ラフソン法では分離区間外の根に収束する場合があった。このため、唯一の実根が含まれる分離区間に対し、二分法を3回適用して1/8に縮小するステップを追加した。冒頭の例2は、二分法の追加により収束性が改善する例である:
リダーズ法による求根
縮小された分離区間に対し、リダーズ法を適用する。
リダーズ法は、不動点反復法と指数関数を用いて連続関数 $f(x)$ の根を逐次近似する求根アルゴリズムである。$x_{0}$ と $x_{2}$ の間の新しい点 $x_{3}$ を、以下の式で求める。[11]
x_3 = x_1 + (x_1 - x_0)\frac{\operatorname{sign}[f(x_0)]f(x_1)}{\sqrt{f(x_1)^2 - f(x_0)f(x_2)}}
今回は、根の探索範囲を指定できること、実装が容易であること、文献[6]の比較評価結果でリダーズ法が優位であることから、リダーズ法を選択した。ニュートン・ラフソン法との比較では、収束が速いことに加え、根を探索する区間を指定できるため、区間外に収束する問題が発生しない、との利点がある。以下は、冒頭の例3の陰伏方程式 $F_0(u)=0$ の各分離区間についての収束グラフである。(左:ニュートン・ラフソン法、右:リダーズ法)
リダーズ法は、ミュラー法など他の求根アルゴリズムより単純だが性能は同等、とされているが、疑問視する意見もある。[12]
今回のサンプル評価では、二分法とリダーズ法の組み合わせで良好な収束特性が示されたが、今後さらに検討を要する。
重根対応
二分法やRidder's法は重根に対応していない。VAG法も非対応だが拡張して、重根に対しては分離区間が十分に短くなるまで分割が反復されるようにして、VAG法の出力の分離区間の中点を根とすることにした。本来、実根分離が目的のヴァンサンの定理/VAG法を、求根の収束計算にも使うため、信頼性や計算効率についてさらに検討を要する。
文献[10]のVAG法の疑似コードを、重根に対応するため以下の通り拡張した。(赤色の箇所)
1 $var \leftarrow (x + 1)^{deg(p)} p(\frac{a + bx}{1 + x})$ の符号変化の数
2 if $var = 0$ then RETURN $\varnothing$;
3 if $var = 1$ then RETURN $\set{(a, b)}$;
4 $m \leftarrow \frac{1}{2}(a + b)$
+ if $b-a \lt M$ then RETURN $\set{(m-A, m+A)}$;
5 if $p(m) \neq 0$ then
6 RETURN VAG($p$, $(a, m)$) $\cup$ VAG($p$, $(m, b)$)
7 else
+ $var \leftarrow (x + 1)^{deg(p)} p(\frac{m-A + (m+A)x}{1 + x})$ の符号変化の数
+ if $var = 1$ then
8 RETURN VAG($p$, $(a, m)$) $\cup$ $\set{[m, m]}$ $\cup$ VAG($p$, $(m, b)$)
+ else
+ RETURN VAG($p$, $(a, m-A)$) $\cup$ $\set{[m-A, m+A]}$ $\cup$ VAG($p$, $(m+A, b)$)
+ end
9 end
-
区間の中点 $m$ における関数値 $p(m)$ が $0$ の場合、区間 $(m-A,m+A)$ の根の数が $1$ であれば分離区間 $[m,m]$ を出力し、$2$ 以上の場合は分離区間 $(m-A,m+A)$ を出力する。
ただし、$A$ は重根の場合の分離区間長の$\frac{1}{2}$である。 -
区間 $(a,b)$ に根が2個以上あっても、区間長 $b-a$ が $M$ より短い場合、分割処理を打ち切り、複数の根が含まれる分離区間 $(m-A,m+A)$ を出力する。
ただし、$M$ は最小の区間長である。 -
出力の分離区間の区間長が $0$ の場合と、区間に含まれる根の数が $2$ 以上の場合は、後段処理(二分法、リダーズ法)をスキップする。後者の場合は区間の中点を根とする。
$M$ と $A$ を独立に設定可能とした理由は、重根の求根精度の確保と、浮動小数点誤差の許容範囲確保を両立するためである。
以下は冒頭の例11(カスプ点どうし接触)の根 $u=0.75$(重複数4)について、分離区間 $(0,0.75-A)$、$[0.75-A,0.75+A]$、$(0.75+A,1)$ それぞれのVAG法の変換多項式の係数をSage Mathを用いて求めたものである。
期待通りの符号変化の数 $\lbrace 0, 4, 0 \rbrace$ を得るためには、分離区間を長め($A$を$10^{-3}$以上)に設定する必要があった。係数の値に鑑みて、浮動小数演算における誤差の影響によるものと推測されるが、解析が必要である。
| $A$ | $(x + 1)^{deg(p)} p(\frac{a + bx}{1 + x})$ の係数と符号変化の数 |
|---|---|
| $10^{-6}$ |  |
| $10^{-5}$ |  |
| $10^{-4}$ |  |
| $10^{-3}$ |  |
交点判定
交点候補のパラメータ $t$ を $x=f_0(t)$、$y=g_0(t)$ にあてはめて曲線 ${\boldsymbol{B}}_0$ 上の交点候補点の座標を求める。また、交点候補のパラメータ $u$ を $x=f_1(u)$、$y=g_1(u)$ にあてはめて曲線 ${\boldsymbol{B}}_1$ 上の交点候補点の座標を求める。
両者を突き合わせてペアになるもの、すなわちユークリッド距離が十分に小さい相手があるものを交点とする。
実装
このアルゴリズムを C++/Qt で実装した。Appendix Eにソースコードを示す。
リダーズ法は[13]に例示されているPythonのコードを、C++に変換して実装した。
数値的な安定性のために以下の対応をした。
- 制御点の座標を、値域が $[0,1]$ になるようアフィン変換してから交点検出し、制御点の元の座標と交点のパラメータから交点の座標を求めるようにした。
- 4次以上の多項式の計算では、乗算と加算を反復するよう変形して実装した。例として
$\quad p(x)=e_0 x^9+e_1 x^8+e_2 x^7+e_3 x^6+e_4 x^5+e_5 x^4+e_6 x^3+e_7 x^2+e_8 x+e_9$
は以下のように実装した:
double p_(double *e, double x){
return ((((((((e[0]*x+e[1])*x+e[2])*x+e[3])*x+e[4])*x+e[5])*x+e[6])*x+e[7])*x+e[8])*x+e[9];
}
- $0$ か否かを判定する場合等、浮動小数点誤差を許容する実装とした。
各しきい値はサンプルを用いて実験的に求めて設定したものであり、今後評価を要する。 - VAG法は疑似コードの通りに再起呼び出しを用いる実装としており、再帰の深さに応じたスタックフレームを確保する必要がある。今回の実装例のvVAGが使用するスタックを実測したところ、最大4624バイトであった。(MSVC2022使用時)
結果
- 複数の例を用いて動作確認を行い、正しい交点が得られることを確認した。
- 求根においては、リダーズ法での収束は十分に速く、安定して根を得られた。
- 陰伏方程式に重根が含まれる場合はVAG法の反復回数が増えるが、現実的な範囲に抑えられた。
考察
Implicitization法の強みは、従来の手法では不安定になりやすい複雑な交差パターンや、ねじれ・重なりを持つケースでも、代数的に交点を求められる点にある。
また、数値的手法を明確に区分け(実根分離 → 実根抽出 → 交点判定)しているため、実装の移植性・汎用性が高く、他の3次パラメトリック曲線(たとえば B-スプライン、Catmull-Romスプライン、さらにはサーフェスなど)への応用可能性もある。
一方で、重根や係数のスケーリング、浮動小数点誤差、求根アルゴリズムの安定性など、実用段階で注意すべき課題がある。特に、重根への対応は簡易的な発案による手法であり、精度保証や理論保証としては不十分である。
結論と今後の展望
本稿では、Implicitization法によるベジェ曲線の交点検出の実用的な手法を提示し、その実装および動作確認を行った。結果として、従来の幾何的手法では難しい交差パターンにも対応可能であり、代数的アプローチの有用性が示された。
今後の課題として、以下が挙げられる。
- 曲線の交差パターンと陰伏方程式の根の類型化:解析的アプローチによる分類と検証
- 求根手法の検討(ミュラー法その他や、複数手法の組み合わせ)
- 重根・近接根へのより厳密な対応
- 数値誤差・丸め誤差に対するロバスト性の強化
- 実際のグラフィックス/CAD/GUIシステムへの応用とその性能評価
- 他のパラメトリック曲線やサーフェスへの拡張
参考文献
[1] T.W. Sederberg, T. Nishita
Curve intersection using Bézier clipping
Computer-Aided Design, Vol.22, Issue 9, Nov.1990, pp.538-549
http://nishitalab.org/user/nis/cdrom/cad/CAGD90Curve.pdf
[2] Thomas W. Sederberg
Computer Aided Geometric Design, pp.191-208
Brigham Young University ScholarsArchive -- Faculty Publications
https://scholarsarchive.byu.edu/facpub/1/
[3] T.W Sederberg, D.C Anderson, R.N Goldman
Implicit representation of parametric curves and surfaces
Computer Vision, Graphics, and Image Processing, Vol.28, Issue 1, Oct.1984, pp.72-84
https://www.sciencedirect.com/science/article/abs/pii/0734189X84901403
[4] ゴッドフット企画
エクセルで操る!デュラン・ケルナー・アバース法(DKA法)による高次代数方程式の解計算
https://godfoot.world.coocan.jp/DKA-Method.htm
[5] PukiWiki for PBCGLab -- 非線形方程式の根
https://pbcglab.jp/cgi-bin/wiki/?%E9%9D%9E%E7%B7%9A%E5%BD%A2%E6%96%B9%E7%A8%8B%E5%BC%8F%E3%81%AE%E6%A0%B9
[6] Alexander Reshetov
Exploiting Budan-Fourier and Vincent’s Theorems for Ray Tracing 3D Bézier Curves
Proceedings of HPG ’17, Los Angeles, CA, USA, July 28-30, 2017
https://research.nvidia.com/publication/2017-07_exploiting-budan-fourier-and-vincents-theorems-ray-tracing-3d-bezier-curves
[7] Gerald Farin
Curves and Surfaces for Computer Aided Geometric Design: A Practical Guide
Academic Press, ISBN 0-12-249050-9, p.42, 1988
[8] Mathematics Stack Exchange -- Quadratic Bezier curves representation as implicit quadratic equation
https://math.stackexchange.com/questions/438743/quadratic-bezier-curves-representation-as-implicit-quadratic-equation
[9] Wikipedia -- ブダンの定理
https://ja.wikipedia.org/wiki/%E3%83%96%E3%83%80%E3%83%B3%E3%81%AE%E5%AE%9A%E7%90%86
[10] Wikipedia -- ヴァンサンの定理
https://ja.wikipedia.org/wiki/%E3%83%B4%E3%82%A1%E3%83%B3%E3%82%B5%E3%83%B3%E3%81%AE%E5%AE%9A%E7%90%86
[11] Wikipedia -- リダーズ法
https://ja.wikipedia.org/wiki/%E3%83%AA%E3%83%80%E3%83%BC%E3%82%BA%E6%B3%95
[12] Mathematics Stack Exchange -- Why does Ridders' method work as well as it does?
https://math.stackexchange.com/questions/1596654/why-does-ridders-method-work-as-well-as-it-does
[13] Jaan Kiusalaas
Numerical Methods in Engineering with Python (2nd ed.)
Cambridge University Press, ISBN 978-0-521-19132-6, pp.147–148, 2010
Appendix
A) 曲線のパラメトリック関数を陰関数に変換(3次用)
Collect[Expand[Eliminate[{a0*t^3+a1*t^2+a2*t+a3==x,b0*t^3+b1*t^2+b2*t+b3==y},t]],{x,y}]
y (-6 a0^2 a3 b0 b3 + 3 a0^2 a3 b1 b2 - a0 a1 a3 b0 b2 - 2 a0 a1 a3 b1^2 + a0 a2 a3 b0 b1 + 3 a0 a3^2 b0^2 + 2 a1^2 a3 b0 b1 - 3 a1 a2 a3 b0^2) + 3 a0^2 a3 b0 b3^2 + 3 a0^2 a3 b0 y^2 - 3 a0^2 a3 b1 b2 b3 + a0^2 a3 b2^3 + x (6 a0 a3 b0^2 b3 - 6 a0 a3 b0^2 y - 6 a0 a3 b0 b1 b2 + 2 a0 a3 b1^3 + 4 a1 a3 b0^2 b2 - 2 a1 a3 b0 b1^2 + 2 a2 a3 b0^2 b1 - 3 a3^2 b0^3) + a0 a1 a3 b0 b2 b3 + 2 a0 a1 a3 b1^2 b3 - a0 a1 a3 b1 b2^2 - a0 a2 a3 b0 b1 b3 - 2 a0 a2 a3 b0 b2^2 + a0 a2 a3 b1^2 b2 - 3 a0 a3^2 b0^2 b3 + 3 a0 a3^2 b0 b1 b2 - a0 a3^2 b1^3 - 2 a1^2 a3 b0 b1 b3 + a1^2 a3 b0 b2^2 + 3 a1 a2 a3 b0^2 b3 - a1 a2 a3 b0 b1 b2 - 2 a1 a3^2 b0^2 b2 + a1 a3^2 b0 b1^2 + a2^2 a3 b0^2 b2 - a2 a3^2 b0^2 b1 + a3^3 b0^3 + 3 a3 b0^3 x^2 = a0^3 b3^3 - a0^3 y^3 + x (y (-6 a0^2 b0 b3 + 3 a0^2 b1 b2 - a0 a1 b0 b2 - 2 a0 a1 b1^2 + a0 a2 b0 b1 + 2 a1^2 b0 b1 - 3 a1 a2 b0^2) + 3 a0^2 b0 b3^2 + 3 a0^2 b0 y^2 - 3 a0^2 b1 b2 b3 + a0^2 b2^3 + a0 a1 b0 b2 b3 + 2 a0 a1 b1^2 b3 - a0 a1 b1 b2^2 - a0 a2 b0 b1 b3 - 2 a0 a2 b0 b2^2 + a0 a2 b1^2 b2 - 2 a1^2 b0 b1 b3 + a1^2 b0 b2^2 + 3 a1 a2 b0^2 b3 - a1 a2 b0 b1 b2 + a2^2 b0^2 b2) - a0^2 a1 b2 b3^2 - 2 a0^2 a2 b1 b3^2 + a0^2 a2 b2^2 b3 + y (-3 a0^3 b3^2 + 2 a0^2 a1 b2 b3 + 4 a0^2 a2 b1 b3 - a0^2 a2 b2^2 - 2 a0 a1^2 b1 b3 - 6 a0 a1 a2 b0 b3 + a0 a1 a2 b1 b2 + 2 a0 a2^2 b0 b2 - a0 a2^2 b1^2 + 2 a1^3 b0 b3 - a1^2 a2 b0 b2 + a1 a2^2 b0 b1 - a2^3 b0^2) + y^2 (3 a0^3 b3 - a0^2 a1 b2 - 2 a0^2 a2 b1 + a0 a1^2 b1 + 3 a0 a1 a2 b0 - a1^3 b0) + a0 a1^2 b1 b3^2 + x^2 (3 a0 b0^2 b3 - 3 a0 b0^2 y - 3 a0 b0 b1 b2 + a0 b1^3 + 2 a1 b0^2 b2 - a1 b0 b1^2 + a2 b0^2 b1) + 3 a0 a1 a2 b0 b3^2 - a0 a1 a2 b1 b2 b3 - 2 a0 a2^2 b0 b2 b3 + a0 a2^2 b1^2 b3 + a1^3 (-b0) b3^2 + a1^2 a2 b0 b2 b3 - a1 a2^2 b0 b1 b3 + a2^3 b0^2 b3 + b0^3 x^3
手作業により、陰関数$F(x,y)=0$の形に整理する。
var('a0 a1 a2 a3')
var('b0 b1 b2 b3')
x=a0*t^3+a1*t^2+a2*t+a3
y=b0*t^3+b1*t^2+b2*t+b3
F3=a3^3*b0^3-a2*a3^2*b0^2*b1+a1*a3^2*b0*b1^2-a0*a3^2*b1^3+a2^2*a3*b0^2*b2-2*a1*a3^2*b0^2*b2-a1*a2*a3*b0*b1*b2+3*a0*a3^2*b0*b1*b2+a0*a2*a3*b1^2*b2+a1^2*a3*b0*b2^2-2*a0*a2*a3*b0*b2^2-a0*a1*a3*b1*b2^2+a0^2*a3*b2^3-a2^3*b0^2*b3+3*a1*a2*a3*b0^2*b3-3*a0*a3^2*b0^2*b3+a1*a2^2*b0*b1*b3-2*a1^2*a3*b0*b1*b3-a0*a2*a3*b0*b1*b3-a0*a2^2*b1^2*b3+2*a0*a1*a3*b1^2*b3-a1^2*a2*b0*b2*b3+2*a0*a2^2*b0*b2*b3+a0*a1*a3*b0*b2*b3+a0*a1*a2*b1*b2*b3-3*a0^2*a3*b1*b2*b3-a0^2*a2*b2^2*b3+a1^3*b0*b3^2-3*a0*a1*a2*b0*b3^2+3*a0^2*a3*b0*b3^2-a0*a1^2*b1*b3^2+2*a0^2*a2*b1*b3^2+a0^2*a1*b2*b3^2-a0^3*b3^3+(-3*a3^2*b0^3+2*a2*a3*b0^2*b1-2*a1*a3*b0*b1^2+2*a0*a3*b1^3-a2^2*b0^2*b2+4*a1*a3*b0^2*b2+a1*a2*b0*b1*b2-6*a0*a3*b0*b1*b2-a0*a2*b1^2*b2-a1^2*b0*b2^2+2*a0*a2*b0*b2^2+a0*a1*b1*b2^2-a0^2*b2^3-3*a1*a2*b0^2*b3+6*a0*a3*b0^2*b3+2*a1^2*b0*b1*b3+a0*a2*b0*b1*b3-2*a0*a1*b1^2*b3-a0*a1*b0*b2*b3+3*a0^2*b1*b2*b3-3*a0^2*b0*b3^2)*x+(a2^3*b0^2-3*a1*a2*a3*b0^2+3*a0*a3^2*b0^2-a1*a2^2*b0*b1+2*a1^2*a3*b0*b1+a0*a2*a3*b0*b1+a0*a2^2*b1^2-2*a0*a1*a3*b1^2+a1^2*a2*b0*b2-2*a0*a2^2*b0*b2-a0*a1*a3*b0*b2-a0*a1*a2*b1*b2+3*a0^2*a3*b1*b2+a0^2*a2*b2^2-2*a1^3*b0*b3+6*a0*a1*a2*b0*b3-6*a0^2*a3*b0*b3+2*a0*a1^2*b1*b3-4*a0^2*a2*b1*b3-2*a0^2*a1*b2*b3+3*a0^3*b3^2)*y+(3*a3*b0^3-a2*b0^2*b1+a1*b0*b1^2-a0*b1^3-2*a1*b0^2*b2+3*a0*b0*b1*b2-3*a0*b0^2*b3)*x^2+(3*a1*a2*b0^2-6*a0*a3*b0^2-2*a1^2*b0*b1-a0*a2*b0*b1+2*a0*a1*b1^2+a0*a1*b0*b2-3*a0^2*b1*b2+6*a0^2*b0*b3)*x*y+(a1^3*b0-3*a0*a1*a2*b0+3*a0^2*a3*b0-a0*a1^2*b1+2*a0^2*a2*b1+a0^2*a1*b2-3*a0^3*b3)*y^2-b0^3*x^3+3*a0*b0^2*x^2*y-3*a0^2*b0*x*y^2+a0^3*y^3
F3.simplify_full()
0
B) 陰伏方程式の各項の係数を求める式を求める
var('u a0 a1 a2 a3 b0 b1 b2 b3 c0 c1 c2 c3 d0 d1 d2 d3')
x=c0*u^3+c1*u^2+c2*u+c3
y=d0*u^3+d1*u^2+d2*u+d3
F0=a3^3*b0^3-a2*a3^2*b0^2*b1+a1*a3^2*b0*b1^2-a0*a3^2*b1^3+a2^2*a3*b0^2*b2-2*a1*a3^2*b0^2*b2-a1*a2*a3*b0*b1*b2+3*a0*a3^2*b0*b1*b2+a0*a2*a3*b1^2*b2+a1^2*a3*b0*b2^2-2*a0*a2*a3*b0*b2^2-a0*a1*a3*b1*b2^2+a0^2*a3*b2^3-a2^3*b0^2*b3+3*a1*a2*a3*b0^2*b3-3*a0*a3^2*b0^2*b3+a1*a2^2*b0*b1*b3-2*a1^2*a3*b0*b1*b3-a0*a2*a3*b0*b1*b3-a0*a2^2*b1^2*b3+2*a0*a1*a3*b1^2*b3-a1^2*a2*b0*b2*b3+2*a0*a2^2*b0*b2*b3+a0*a1*a3*b0*b2*b3+a0*a1*a2*b1*b2*b3-3*a0^2*a3*b1*b2*b3-a0^2*a2*b2^2*b3+a1^3*b0*b3^2-3*a0*a1*a2*b0*b3^2+3*a0^2*a3*b0*b3^2-a0*a1^2*b1*b3^2+2*a0^2*a2*b1*b3^2+a0^2*a1*b2*b3^2-a0^3*b3^3+(-3*a3^2*b0^3+2*a2*a3*b0^2*b1-2*a1*a3*b0*b1^2+2*a0*a3*b1^3-a2^2*b0^2*b2+4*a1*a3*b0^2*b2+a1*a2*b0*b1*b2-6*a0*a3*b0*b1*b2-a0*a2*b1^2*b2-a1^2*b0*b2^2+2*a0*a2*b0*b2^2+a0*a1*b1*b2^2-a0^2*b2^3-3*a1*a2*b0^2*b3+6*a0*a3*b0^2*b3+2*a1^2*b0*b1*b3+a0*a2*b0*b1*b3-2*a0*a1*b1^2*b3-a0*a1*b0*b2*b3+3*a0^2*b1*b2*b3-3*a0^2*b0*b3^2)*x+(a2^3*b0^2-3*a1*a2*a3*b0^2+3*a0*a3^2*b0^2-a1*a2^2*b0*b1+2*a1^2*a3*b0*b1+a0*a2*a3*b0*b1+a0*a2^2*b1^2-2*a0*a1*a3*b1^2+a1^2*a2*b0*b2-2*a0*a2^2*b0*b2-a0*a1*a3*b0*b2-a0*a1*a2*b1*b2+3*a0^2*a3*b1*b2+a0^2*a2*b2^2-2*a1^3*b0*b3+6*a0*a1*a2*b0*b3-6*a0^2*a3*b0*b3+2*a0*a1^2*b1*b3-4*a0^2*a2*b1*b3-2*a0^2*a1*b2*b3+3*a0^3*b3^2)*y+(3*a3*b0^3-a2*b0^2*b1+a1*b0*b1^2-a0*b1^3-2*a1*b0^2*b2+3*a0*b0*b1*b2-3*a0*b0^2*b3)*x^2+(3*a1*a2*b0^2-6*a0*a3*b0^2-2*a1^2*b0*b1-a0*a2*b0*b1+2*a0*a1*b1^2+a0*a1*b0*b2-3*a0^2*b1*b2+6*a0^2*b0*b3)*x*y+(a1^3*b0-3*a0*a1*a2*b0+3*a0^2*a3*b0-a0*a1^2*b1+2*a0^2*a2*b1+a0^2*a1*b2-3*a0^3*b3)*y^2-b0^3*x^3+3*a0*b0^2*x^2*y-3*a0^2*b0*x*y^2+a0^3*y^3
cf0=F0.coefficients(u,sparse=False)
cf0[9].simplify_full()
cf0[8].simplify_full()
cf0[7].simplify_full()
cf0[6].simplify_full()
cf0[5].simplify_full()
cf0[4].simplify_full()
cf0[3].simplify_full()
cf0[2].simplify_full()
cf0[1].simplify_full()
cf0[0].simplify_full()
-b0^3*c0^3 + 3*a0*b0^2*c0^2*d0 - 3*a0^2*b0*c0*d0^2 + a0^3*d0^3
-3*b0^3*c0^2*c1 + 6*a0*b0^2*c0*c1*d0 - 3*a0^2*b0*c1*d0^2 + 3*(a0*b0^2*c0^2 - 2*a0^2*b0*c0*d0 + a0^3*d0^2)*d1
-3*b0^3*c0*c1^2 - 3*b0^3*c0^2*c2 - 3*a0^2*b0*c2*d0^2 - 3*(a0^2*b0*c0 - a0^3*d0)*d1^2 + 3*(a0*b0^2*c1^2 + 2*a0*b0^2*c0*c2)*d0 + 6*(a0*b0^2*c0*c1 - a0^2*b0*c1*d0)*d1 + 3*(a0*b0^2*c0^2 - 2*a0^2*b0*c0*d0 + a0^3*d0^2)*d2
-b0^3*c1^3 - 6*b0^3*c0*c1*c2 - 3*b0^3*c0^2*c3 - 3*a0^2*b0*c1*d1^2 + a0^3*d1^3 + (3*a3*b0^3 - a2*b0^2*b1 + a1*b0*b1^2 - a0*b1^3 - 3*a0*b0^2*b3 - (2*a1*b0^2 - 3*a0*b0*b1)*b2)*c0^2 + (a0^2*a1*b2 - 3*a0^3*b3 - 3*a0^2*b0*c3 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*d0^2 + (6*a0*b0^2*c1*c2 + 6*a0*b0^2*c0*c3 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c0)*d0 + 3*(a0*b0^2*c1^2 + 2*a0*b0^2*c0*c2 - 2*a0^2*b0*c2*d0)*d1 + 6*(a0*b0^2*c0*c1 - a0^2*b0*c1*d0 - (a0^2*b0*c0 - a0^3*d0)*d1)*d2 + 3*(a0*b0^2*c0^2 - 2*a0^2*b0*c0*d0 + a0^3*d0^2)*d3
-3*b0^3*c1^2*c2 - 3*b0^3*c0*c2^2 - 6*b0^3*c0*c1*c3 - 3*a0^2*b0*c2*d1^2 + 2*(3*a3*b0^3 - a2*b0^2*b1 + a1*b0*b1^2 - a0*b1^3 - 3*a0*b0^2*b3 - (2*a1*b0^2 - 3*a0*b0*b1)*b2)*c0*c1 - 3*(a0^2*b0*c0 - a0^3*d0)*d2^2 + (3*a0*b0^2*c2^2 + 6*a0*b0^2*c1*c3 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c1)*d0 + (6*a0*b0^2*c1*c2 + 6*a0*b0^2*c0*c3 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c0 + 2*(a0^2*a1*b2 - 3*a0^3*b3 - 3*a0^2*b0*c3 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*d0)*d1 + 3*(a0*b0^2*c1^2 + 2*a0*b0^2*c0*c2 - 2*a0^2*b0*c2*d0 - 2*a0^2*b0*c1*d1 + a0^3*d1^2)*d2 + 6*(a0*b0^2*c0*c1 - a0^2*b0*c1*d0 - (a0^2*b0*c0 - a0^3*d0)*d1)*d3
-3*b0^3*c1*c2^2 + (3*a3*b0^3 - a2*b0^2*b1 + a1*b0*b1^2 - a0*b1^3 - 3*a0*b0^2*b3 - (2*a1*b0^2 - 3*a0*b0*b1)*b2)*c1^2 + 2*(3*a3*b0^3 - a2*b0^2*b1 + a1*b0*b1^2 - a0*b1^3 - 3*a0*b0^2*b3 - (2*a1*b0^2 - 3*a0*b0*b1)*b2)*c0*c2 + (a0^2*a1*b2 - 3*a0^3*b3 - 3*a0^2*b0*c3 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*d1^2 - 3*(a0^2*b0*c1 - a0^3*d1)*d2^2 - 3*(b0^3*c1^2 + 2*b0^3*c0*c2)*c3 + (6*a0*b0^2*c2*c3 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c2)*d0 + (3*a0*b0^2*c2^2 + 6*a0*b0^2*c1*c3 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c1)*d1 + (6*a0*b0^2*c1*c2 + 6*a0*b0^2*c0*c3 - 6*a0^2*b0*c2*d1 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c0 + 2*(a0^2*a1*b2 - 3*a0^3*b3 - 3*a0^2*b0*c3 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*d0)*d2 + 3*(a0*b0^2*c1^2 + 2*a0*b0^2*c0*c2 - 2*a0^2*b0*c2*d0 - 2*a0^2*b0*c1*d1 + a0^3*d1^2 - 2*(a0^2*b0*c0 - a0^3*d0)*d2)*d3
-b0^3*c2^3 - 3*b0^3*c0*c3^2 - 3*a0^2*b0*c2*d2^2 + a0^3*d2^3 + 2*(3*a3*b0^3 - a2*b0^2*b1 + a1*b0*b1^2 - a0*b1^3 - 3*a0*b0^2*b3 - (2*a1*b0^2 - 3*a0*b0*b1)*b2)*c1*c2 - 3*(a0^2*b0*c0 - a0^3*d0)*d3^2 - (3*a3^2*b0^3 - 2*a2*a3*b0^2*b1 + 2*a1*a3*b0*b1^2 - 2*a0*a3*b1^3 + a0^2*b2^3 + 3*a0^2*b0*b3^2 - (a0*a1*b1 - (a1^2 - 2*a0*a2)*b0)*b2^2 + (a0*a2*b1^2 + (a2^2 - 4*a1*a3)*b0^2 - (a1*a2 - 6*a0*a3)*b0*b1)*b2 + (2*a0*a1*b1^2 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*b3)*c0 - 2*(3*b0^3*c1*c2 - (3*a3*b0^3 - a2*b0^2*b1 + a1*b0*b1^2 - a0*b1^3 - 3*a0*b0^2*b3 - (2*a1*b0^2 - 3*a0*b0*b1)*b2)*c0)*c3 + (a0^2*a2*b2^2 + 3*a0^3*b3^2 + 3*a0*b0^2*c3^2 + (a2^3 - 3*a1*a2*a3 + 3*a0*a3^2)*b0^2 - (a1*a2^2 - (2*a1^2 + a0*a2)*a3)*b0*b1 + (a0*a2^2 - 2*a0*a1*a3)*b1^2 + ((a1^2*a2 - 2*a0*a2^2 - a0*a1*a3)*b0 - (a0*a1*a2 - 3*a0^2*a3)*b1)*b2 - 2*(a0^2*a1*b2 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*b3 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c3)*d0 + (6*a0*b0^2*c2*c3 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c2)*d1 + (3*a0*b0^2*c2^2 + 6*a0*b0^2*c1*c3 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c1 + 2*(a0^2*a1*b2 - 3*a0^3*b3 - 3*a0^2*b0*c3 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*d1)*d2 + (6*a0*b0^2*c1*c2 + 6*a0*b0^2*c0*c3 - 6*a0^2*b0*c2*d1 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c0 + 2*(a0^2*a1*b2 - 3*a0^3*b3 - 3*a0^2*b0*c3 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*d0 - 6*(a0^2*b0*c1 - a0^3*d1)*d2)*d3
-3*b0^3*c1*c3^2 + (3*a3*b0^3 - a2*b0^2*b1 + a1*b0*b1^2 - a0*b1^3 - 3*a0*b0^2*b3 - (2*a1*b0^2 - 3*a0*b0*b1)*b2)*c2^2 + (a0^2*a1*b2 - 3*a0^3*b3 - 3*a0^2*b0*c3 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*d2^2 - 3*(a0^2*b0*c1 - a0^3*d1)*d3^2 - (3*a3^2*b0^3 - 2*a2*a3*b0^2*b1 + 2*a1*a3*b0*b1^2 - 2*a0*a3*b1^3 + a0^2*b2^3 + 3*a0^2*b0*b3^2 - (a0*a1*b1 - (a1^2 - 2*a0*a2)*b0)*b2^2 + (a0*a2*b1^2 + (a2^2 - 4*a1*a3)*b0^2 - (a1*a2 - 6*a0*a3)*b0*b1)*b2 + (2*a0*a1*b1^2 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*b3)*c1 - (3*b0^3*c2^2 - 2*(3*a3*b0^3 - a2*b0^2*b1 + a1*b0*b1^2 - a0*b1^3 - 3*a0*b0^2*b3 - (2*a1*b0^2 - 3*a0*b0*b1)*b2)*c1)*c3 + (a0^2*a2*b2^2 + 3*a0^3*b3^2 + 3*a0*b0^2*c3^2 + (a2^3 - 3*a1*a2*a3 + 3*a0*a3^2)*b0^2 - (a1*a2^2 - (2*a1^2 + a0*a2)*a3)*b0*b1 + (a0*a2^2 - 2*a0*a1*a3)*b1^2 + ((a1^2*a2 - 2*a0*a2^2 - a0*a1*a3)*b0 - (a0*a1*a2 - 3*a0^2*a3)*b1)*b2 - 2*(a0^2*a1*b2 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*b3 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c3)*d1 + (6*a0*b0^2*c2*c3 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c2)*d2 + (3*a0*b0^2*c2^2 + 6*a0*b0^2*c1*c3 - 6*a0^2*b0*c2*d2 + 3*a0^3*d2^2 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c1 + 2*(a0^2*a1*b2 - 3*a0^3*b3 - 3*a0^2*b0*c3 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*d1)*d3
-3*b0^3*c2*c3^2 + 2*(3*a3*b0^3 - a2*b0^2*b1 + a1*b0*b1^2 - a0*b1^3 - 3*a0*b0^2*b3 - (2*a1*b0^2 - 3*a0*b0*b1)*b2)*c2*c3 - 3*(a0^2*b0*c2 - a0^3*d2)*d3^2 - (3*a3^2*b0^3 - 2*a2*a3*b0^2*b1 + 2*a1*a3*b0*b1^2 - 2*a0*a3*b1^3 + a0^2*b2^3 + 3*a0^2*b0*b3^2 - (a0*a1*b1 - (a1^2 - 2*a0*a2)*b0)*b2^2 + (a0*a2*b1^2 + (a2^2 - 4*a1*a3)*b0^2 - (a1*a2 - 6*a0*a3)*b0*b1)*b2 + (2*a0*a1*b1^2 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*b3)*c2 + (a0^2*a2*b2^2 + 3*a0^3*b3^2 + 3*a0*b0^2*c3^2 + (a2^3 - 3*a1*a2*a3 + 3*a0*a3^2)*b0^2 - (a1*a2^2 - (2*a1^2 + a0*a2)*a3)*b0*b1 + (a0*a2^2 - 2*a0*a1*a3)*b1^2 + ((a1^2*a2 - 2*a0*a2^2 - a0*a1*a3)*b0 - (a0*a1*a2 - 3*a0^2*a3)*b1)*b2 - 2*(a0^2*a1*b2 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*b3 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c3)*d2 + (6*a0*b0^2*c2*c3 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c2 + 2*(a0^2*a1*b2 - 3*a0^3*b3 - 3*a0^2*b0*c3 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*d2)*d3
a3^3*b0^3 - a2*a3^2*b0^2*b1 + a1*a3^2*b0*b1^2 - a0*a3^2*b1^3 + a0^2*a3*b2^3 - a0^3*b3^3 - b0^3*c3^3 + a0^3*d3^3 - (a0*a1*a3*b1 - (a1^2 - 2*a0*a2)*a3*b0)*b2^2 + (a0^2*a1*b2 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*b3^2 + (3*a3*b0^3 - a2*b0^2*b1 + a1*b0*b1^2 - a0*b1^3 - 3*a0*b0^2*b3 - (2*a1*b0^2 - 3*a0*b0*b1)*b2)*c3^2 + (a0^2*a1*b2 - 3*a0^3*b3 - 3*a0^2*b0*c3 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*d3^2 + (a0*a2*a3*b1^2 + (a2^2*a3 - 2*a1*a3^2)*b0^2 - (a1*a2*a3 - 3*a0*a3^2)*b0*b1)*b2 - (a0^2*a2*b2^2 + (a2^3 - 3*a1*a2*a3 + 3*a0*a3^2)*b0^2 - (a1*a2^2 - (2*a1^2 + a0*a2)*a3)*b0*b1 + (a0*a2^2 - 2*a0*a1*a3)*b1^2 + ((a1^2*a2 - 2*a0*a2^2 - a0*a1*a3)*b0 - (a0*a1*a2 - 3*a0^2*a3)*b1)*b2)*b3 - (3*a3^2*b0^3 - 2*a2*a3*b0^2*b1 + 2*a1*a3*b0*b1^2 - 2*a0*a3*b1^3 + a0^2*b2^3 + 3*a0^2*b0*b3^2 - (a0*a1*b1 - (a1^2 - 2*a0*a2)*b0)*b2^2 + (a0*a2*b1^2 + (a2^2 - 4*a1*a3)*b0^2 - (a1*a2 - 6*a0*a3)*b0*b1)*b2 + (2*a0*a1*b1^2 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*b3)*c3 + (a0^2*a2*b2^2 + 3*a0^3*b3^2 + 3*a0*b0^2*c3^2 + (a2^3 - 3*a1*a2*a3 + 3*a0*a3^2)*b0^2 - (a1*a2^2 - (2*a1^2 + a0*a2)*a3)*b0*b1 + (a0*a2^2 - 2*a0*a1*a3)*b1^2 + ((a1^2*a2 - 2*a0*a2^2 - a0*a1*a3)*b0 - (a0*a1*a2 - 3*a0^2*a3)*b1)*b2 - 2*(a0^2*a1*b2 + (a1^3 - 3*a0*a1*a2 + 3*a0^2*a3)*b0 - (a0*a1^2 - 2*a0^2*a2)*b1)*b3 + (2*a0*a1*b1^2 + 6*a0^2*b0*b3 + 3*(a1*a2 - 2*a0*a3)*b0^2 - (2*a1^2 + a0*a2)*b0*b1 + (a0*a1*b0 - 3*a0^2*b1)*b2)*c3)*d3
var('u a1 a2 a3 b1 b2 b3 c0 c1 c2 c3 d0 d1 d2 d3')
x=c0*u^3+c1*u^2+c2*u+c3
y=d0*u^3+d1*u^2+d2*u+d3
F0=a3^2*b1^2-a2*a3*b1*b2+a1*a3*b2^2+a2^2*b1*b3-2*a1*a3*b1*b3-a1*a2*b2*b3+a1^2*b3^2+(-2*a3*b1^2+a2*b1*b2-a1*b2^2+2*a1*b1*b3)*x+(-a2^2*b1+2*a1*a3*b1+a1*a2*b2-2*a1^2*b3)*y+b1^2*x^2-2*a1*b1*x*y+a1^2*y^2
cf0=F0.coefficients(u,sparse=False)
cf0[6].simplify_full()
cf0[5].simplify_full()
cf0[4].simplify_full()
cf0[3].simplify_full()
cf0[2].simplify_full()
cf0[1].simplify_full()
cf0[0].simplify_full()
b1^2*c0^2 - 2*a1*b1*c0*d0 + a1^2*d0^2
2*b1^2*c0*c1 - 2*a1*b1*c1*d0 - 2*(a1*b1*c0 - a1^2*d0)*d1
b1^2*c1^2 + 2*b1^2*c0*c2 - 2*a1*b1*c2*d0 - 2*a1*b1*c1*d1 + a1^2*d1^2 - 2*(a1*b1*c0 - a1^2*d0)*d2
2*b1^2*c1*c2 + 2*b1^2*c0*c3 - 2*a1*b1*c2*d1 - (2*a3*b1^2 - a2*b1*b2 + a1*b2^2 - 2*a1*b1*b3)*c0 + (a1*a2*b2 - 2*a1^2*b3 - 2*a1*b1*c3 - (a2^2 - 2*a1*a3)*b1)*d0 - 2*(a1*b1*c1 - a1^2*d1)*d2 - 2*(a1*b1*c0 - a1^2*d0)*d3
b1^2*c2^2 + 2*b1^2*c1*c3 - 2*a1*b1*c2*d2 + a1^2*d2^2 - (2*a3*b1^2 - a2*b1*b2 + a1*b2^2 - 2*a1*b1*b3)*c1 + (a1*a2*b2 - 2*a1^2*b3 - 2*a1*b1*c3 - (a2^2 - 2*a1*a3)*b1)*d1 - 2*(a1*b1*c1 - a1^2*d1)*d3
2*b1^2*c2*c3 - (2*a3*b1^2 - a2*b1*b2 + a1*b2^2 - 2*a1*b1*b3)*c2 + (a1*a2*b2 - 2*a1^2*b3 - 2*a1*b1*c3 - (a2^2 - 2*a1*a3)*b1)*d2 - 2*(a1*b1*c2 - a1^2*d2)*d3
a3^2*b1^2 - a2*a3*b1*b2 + a1*a3*b2^2 + a1^2*b3^2 + b1^2*c3^2 + a1^2*d3^2 - (a1*a2*b2 - (a2^2 - 2*a1*a3)*b1)*b3 - (2*a3*b1^2 - a2*b1*b2 + a1*b2^2 - 2*a1*b1*b3)*c3 + (a1*a2*b2 - 2*a1^2*b3 - 2*a1*b1*c3 - (a2^2 - 2*a1*a3)*b1)*d3
var('u a2 a3 b2 b3 c0 c1 c2 c3 d0 d1 d2 d3')
x=c0*u^3+c1*u^2+c2*u+c3
y=d0*u^3+d1*u^2+d2*u+d3
F0=-a3*b2+a2*b3+b2*x-a2*y
cf0=F0.coefficients(u,sparse=False)
cf0[3].simplify_full()
cf0[2].simplify_full()
cf0[1].simplify_full()
cf0[0].simplify_full()
b2*c0 - a2*d0
b2*c1 - a2*d1
b2*c2 - a2*d2
-a3*b2 + a2*b3 + b2*c3 - a2*d3
C) ブダンの命題の変換多項式の係数を求める式を求める
変換多項式:$p(x+1)$
var('x e0 e1 e2 e3 e4 e5 e6 e7 e8 e9')
x1=x+1
p=e0*x1^9+e1*x1^8+e2*x1^7+e3*x1^6+e4*x1^5+e5*x1^4+e6*x1^3+e7*x1^2+e8*x1+e9
p=p.simplify_full()
p.coefficients(x)
[[e0 + e1 + e2 + e3 + e4 + e5 + e6 + e7 + e8 + e9, 0],
[9*e0 + 8*e1 + 7*e2 + 6*e3 + 5*e4 + 4*e5 + 3*e6 + 2*e7 + e8, 1],
[36*e0 + 28*e1 + 21*e2 + 15*e3 + 10*e4 + 6*e5 + 3*e6 + e7, 2],
[84*e0 + 56*e1 + 35*e2 + 20*e3 + 10*e4 + 4*e5 + e6, 3],
[126*e0 + 70*e1 + 35*e2 + 15*e3 + 5*e4 + e5, 4],
[126*e0 + 56*e1 + 21*e2 + 6*e3 + e4, 5],
[84*e0 + 28*e1 + 7*e2 + e3, 6],
[36*e0 + 8*e1 + e2, 7],
[9*e0 + e1, 8],
[e0, 9]]
D) VAG法の変換多項式の係数を求める式を求める
変換多項式:$ (x+1)^9 p \left (\frac{a+bx}{1+x} \right ) $
var('x a b e0 e1 e2 e3 e4 e5 e6 e7 e8 e9')
x1=(a+b*x)/(1+x)
p=e0*x1^9+e1*x1^8+e2*x1^7+e3*x1^6+e4*x1^5+e5*x1^4+e6*x1^3+e7*x1^2+e8*x1+e9
f=(x+1)^9*p
f=f.simplify_full()
f.coefficients(x)
[[a^9*e0 + a^8*e1 + a^7*e2 + a^6*e3 + a^5*e4 + a^4*e5 + a^3*e6 + a^2*e7 + a*e8 + e9,
0],
[a^8*e1 + 2*a^7*e2 + 3*a^6*e3 + 4*a^5*e4 + 5*a^4*e5 + 6*a^3*e6 + 7*a^2*e7 + 8*a*e8 + (9*a^8*e0 + 8*a^7*e1 + 7*a^6*e2 + 6*a^5*e3 + 5*a^4*e4 + 4*a^3*e5 + 3*a^2*e6 + 2*a*e7 + e8)*b + 9*e9,
1],
[a^7*e2 + 3*a^6*e3 + 6*a^5*e4 + 10*a^4*e5 + 15*a^3*e6 + 21*a^2*e7 + (36*a^7*e0 + 28*a^6*e1 + 21*a^5*e2 + 15*a^4*e3 + 10*a^3*e4 + 6*a^2*e5 + 3*a*e6 + e7)*b^2 + 28*a*e8 + 2*(4*a^7*e1 + 7*a^6*e2 + 9*a^5*e3 + 10*a^4*e4 + 10*a^3*e5 + 9*a^2*e6 + 7*a*e7 + 4*e8)*b + 36*e9,
2],
[a^6*e3 + 4*a^5*e4 + 10*a^4*e5 + 20*a^3*e6 + (84*a^6*e0 + 56*a^5*e1 + 35*a^4*e2 + 20*a^3*e3 + 10*a^2*e4 + 4*a*e5 + e6)*b^3 + 35*a^2*e7 + (28*a^6*e1 + 42*a^5*e2 + 45*a^4*e3 + 40*a^3*e4 + 30*a^2*e5 + 18*a*e6 + 7*e7)*b^2 + 56*a*e8 + (7*a^6*e2 + 18*a^5*e3 + 30*a^4*e4 + 40*a^3*e5 + 45*a^2*e6 + 42*a*e7 + 28*e8)*b + 84*e9,
3],
[a^5*e4 + 5*a^4*e5 + (126*a^5*e0 + 70*a^4*e1 + 35*a^3*e2 + 15*a^2*e3 + 5*a*e4 + e5)*b^4 + 15*a^3*e6 + 2*(28*a^5*e1 + 35*a^4*e2 + 30*a^3*e3 + 20*a^2*e4 + 10*a*e5 + 3*e6)*b^3 + 35*a^2*e7 + 3*(7*a^5*e2 + 15*a^4*e3 + 20*a^3*e4 + 20*a^2*e5 + 15*a*e6 + 7*e7)*b^2 + 70*a*e8 + 2*(3*a^5*e3 + 10*a^4*e4 + 20*a^3*e5 + 30*a^2*e6 + 35*a*e7 + 28*e8)*b + 126*e9,
4],
[(126*a^4*e0 + 56*a^3*e1 + 21*a^2*e2 + 6*a*e3 + e4)*b^5 + a^4*e5 + 5*(14*a^4*e1 + 14*a^3*e2 + 9*a^2*e3 + 4*a*e4 + e5)*b^4 + 6*a^3*e6 + 5*(7*a^4*e2 + 12*a^3*e3 + 12*a^2*e4 + 8*a*e5 + 3*e6)*b^3 + 21*a^2*e7 + 5*(3*a^4*e3 + 8*a^3*e4 + 12*a^2*e5 + 12*a*e6 + 7*e7)*b^2 + 56*a*e8 + 5*(a^4*e4 + 4*a^3*e5 + 9*a^2*e6 + 14*a*e7 + 14*e8)*b + 126*e9,
5],
[(84*a^3*e0 + 28*a^2*e1 + 7*a*e2 + e3)*b^6 + 2*(28*a^3*e1 + 21*a^2*e2 + 9*a*e3 + 2*e4)*b^5 + 5*(7*a^3*e2 + 9*a^2*e3 + 6*a*e4 + 2*e5)*b^4 + a^3*e6 + 20*(a^3*e3 + 2*a^2*e4 + 2*a*e5 + e6)*b^3 + 7*a^2*e7 + 5*(2*a^3*e4 + 6*a^2*e5 + 9*a*e6 + 7*e7)*b^2 + 28*a*e8 + 2*(2*a^3*e5 + 9*a^2*e6 + 21*a*e7 + 28*e8)*b + 84*e9,
6],
[(36*a^2*e0 + 8*a*e1 + e2)*b^7 + (28*a^2*e1 + 14*a*e2 + 3*e3)*b^6 + 3*(7*a^2*e2 + 6*a*e3 + 2*e4)*b^5 + 5*(3*a^2*e3 + 4*a*e4 + 2*e5)*b^4 + 5*(2*a^2*e4 + 4*a*e5 + 3*e6)*b^3 + a^2*e7 + 3*(2*a^2*e5 + 6*a*e6 + 7*e7)*b^2 + 8*a*e8 + (3*a^2*e6 + 14*a*e7 + 28*e8)*b + 36*e9,
7],
[(9*a*e0 + e1)*b^8 + 2*(4*a*e1 + e2)*b^7 + (7*a*e2 + 3*e3)*b^6 + 2*(3*a*e3 + 2*e4)*b^5 + 5*(a*e4 + e5)*b^4 + 2*(2*a*e5 + 3*e6)*b^3 + (3*a*e6 + 7*e7)*b^2 + a*e8 + 2*(a*e7 + 4*e8)*b + 9*e9,
8],
[e0*b^9 + e1*b^8 + e2*b^7 + e3*b^6 + e4*b^5 + e5*b^4 + e6*b^3 + e7*b^2 + e8*b + e9,
9]]
E) 実装例ソースコード
#include <cmath>
#include <QPointF>
#include <QList>
using namespace std;
#define EZERO 1e-14 // これより0に近い値は0とする
#define ABADJ 1e-3 // VAG法 重根の分離区間長/2
#define ABMIN 1e-5 // VAG法 分離区間長の最小
#define DSTMIN 1e-4 // 交点候補の突き合わせ判定の距離しきい値
#define PW3(x) ((x)*(x)*(x))
#define PW2(x) ((x)*(x))
typedef struct{
double a; // 区間from
double b; // 区間to
double pa; // aの関数値
double pb; // bの関数値
int nr; // 区間に含まれる実根の数
}Interval;
// 3次ベジェ曲線の係数を求める
void coefBezier(
QList<QPointF> &cp, // IN ベジェ曲線 制御点
double *a, // OUT x係数
double *b) // OUT y係数
{
a[0]=-cp[0].x()+3*cp[1].x()-3*cp[2].x()+cp[3].x();
a[1]=3*cp[0].x()-6*cp[1].x()+3*cp[2].x();
a[2]=-3*cp[0].x()+3*cp[1].x();
a[3]=cp[0].x();
b[0]=-cp[0].y()+3*cp[1].y()-3*cp[2].y()+cp[3].y();
b[1]=3*cp[0].y()-6*cp[1].y()+3*cp[2].y();
b[2]=-3*cp[0].y()+3*cp[1].y();
b[3]=cp[0].y();
}
// 3次パラメトリック曲線の座標を求める
QPointF pointBezier(
double *a, // IN x係数
double *b, // IN y係数
double t) // IN パラメータ
{
return QPointF(a[0]*PW3(t)+a[1]*PW2(t)+a[2]*t+a[3],
b[0]*PW3(t)+b[1]*PW2(t)+b[2]*t+b[3]);
}
// 制御点の座標値を[0,1]に正規化
void normCP(
QList<QPointF> &cp0, // IN 曲線0の制御点
QList<QPointF> &cp1, // IN 曲線1の制御点
QList<QPointF> &ncp0, // OUT 曲線0の制御点(正規化)
QList<QPointF> &ncp1) // OUT 曲線0の制御点(正規化)
{
double xmin=cp0[0].x();
double xmax=cp0[0].x();
double ymin=cp0[0].y();
double ymax=cp0[0].y();
foreach(QPointF p,cp0.mid(1)){
if(xmin>p.x()) xmin=p.x();
if(xmax<p.x()) xmax=p.x();
if(ymin>p.y()) ymin=p.y();
if(ymax<p.y()) ymax=p.y();
}
foreach(QPointF p,cp1){
if(xmin>p.x()) xmin=p.x();
if(xmax<p.x()) xmax=p.x();
if(ymin>p.y()) ymin=p.y();
if(ymax<p.y()) ymax=p.y();
}
double m=max(xmax-xmin,ymax-ymin);
ncp0.clear();
ncp1.clear();
foreach(QPointF p,cp0)
ncp0<<QPointF((p.x()-xmin)/m,(p.y()-ymin)/m);
foreach(QPointF p,cp1)
ncp1<<QPointF((p.x()-xmin)/m,(p.y()-ymin)/m);
}
// 3次パラメトリック曲線どうしの交点の陰伏方程式F0(u)の係数を求める
void coefImp0(
double *a, // IN 曲線0 (x,y)=f(t)の係数列 a[0],b[0]が3次項の係数
double *b,
double *c, // IN 曲線1 (x,y)=g(u)の係数列 c[0],d[0]が3次項の係数
double *d,
double *cf) // OUT F0(u)の係数列 cf[0]が9次項の係数
{
if(abs(a[0])>=EZERO||abs(b[0])>=EZERO){
// 曲線0は3次
cf[0]=-PW3(b[0])*PW3(c[0])+3*a[0]*PW2(b[0])*PW2(c[0])*d[0]-3*PW2(a[0])*b[0]*c[0]*PW2(d[0])+PW3(a[0])*PW3(d[0]);
cf[1]=-3*PW3(b[0])*PW2(c[0])*c[1]+6*a[0]*PW2(b[0])*c[0]*c[1]*d[0]-3*PW2(a[0])*b[0]*c[1]*PW2(d[0])+3*(a[0]*PW2(b[0])*PW2(c[0])-2*PW2(a[0])*b[0]*c[0]*d[0]+PW3(a[0])*PW2(d[0]))*d[1];
cf[2]=-3*PW3(b[0])*c[0]*PW2(c[1])-3*PW3(b[0])*PW2(c[0])*c[2]-3*PW2(a[0])*b[0]*c[2]*PW2(d[0])-3*(PW2(a[0])*b[0]*c[0]-PW3(a[0])*d[0])*PW2(d[1])+3*(a[0]*PW2(b[0])*PW2(c[1])+2*a[0]*PW2(b[0])*c[0]*c[2])*d[0]+6*(a[0]*PW2(b[0])*c[0]*c[1]-PW2(a[0])*b[0]*c[1]*d[0])*d[1]+3*(a[0]*PW2(b[0])*PW2(c[0])-2*PW2(a[0])*b[0]*c[0]*d[0]+PW3(a[0])*PW2(d[0]))*d[2];
cf[3]=-PW3(b[0])*PW3(c[1])-6*PW3(b[0])*c[0]*c[1]*c[2]-3*PW3(b[0])*PW2(c[0])*c[3]-3*PW2(a[0])*b[0]*c[1]*PW2(d[1])+PW3(a[0])*PW3(d[1])+(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*PW2(c[0])+(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*PW2(d[0])+(6*a[0]*PW2(b[0])*c[1]*c[2]+6*a[0]*PW2(b[0])*c[0]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[0])*d[0]+3*(a[0]*PW2(b[0])*PW2(c[1])+2*a[0]*PW2(b[0])*c[0]*c[2]-2*PW2(a[0])*b[0]*c[2]*d[0])*d[1]+6*(a[0]*PW2(b[0])*c[0]*c[1]-PW2(a[0])*b[0]*c[1]*d[0]-(PW2(a[0])*b[0]*c[0]-PW3(a[0])*d[0])*d[1])*d[2]+3*(a[0]*PW2(b[0])*PW2(c[0])-2*PW2(a[0])*b[0]*c[0]*d[0]+PW3(a[0])*PW2(d[0]))*d[3];
cf[4]=-3*PW3(b[0])*PW2(c[1])*c[2]-3*PW3(b[0])*c[0]*PW2(c[2])-6*PW3(b[0])*c[0]*c[1]*c[3]-3*PW2(a[0])*b[0]*c[2]*PW2(d[1])+2*(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*c[0]*c[1]-3*(PW2(a[0])*b[0]*c[0]-PW3(a[0])*d[0])*PW2(d[2])+(3*a[0]*PW2(b[0])*PW2(c[2])+6*a[0]*PW2(b[0])*c[1]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[1])*d[0]+(6*a[0]*PW2(b[0])*c[1]*c[2]+6*a[0]*PW2(b[0])*c[0]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[0]+2*(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*d[0])*d[1]+3*(a[0]*PW2(b[0])*PW2(c[1])+2*a[0]*PW2(b[0])*c[0]*c[2]-2*PW2(a[0])*b[0]*c[2]*d[0]-2*PW2(a[0])*b[0]*c[1]*d[1]+PW3(a[0])*PW2(d[1]))*d[2]+6*(a[0]*PW2(b[0])*c[0]*c[1]-PW2(a[0])*b[0]*c[1]*d[0]-(PW2(a[0])*b[0]*c[0]-PW3(a[0])*d[0])*d[1])*d[3];
cf[5]=-3*PW3(b[0])*c[1]*PW2(c[2])+(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*PW2(c[1])+2*(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*c[0]*c[2]+(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*PW2(d[1])-3*(PW2(a[0])*b[0]*c[1]-PW3(a[0])*d[1])*PW2(d[2])-3*(PW3(b[0])*PW2(c[1])+2*PW3(b[0])*c[0]*c[2])*c[3]+(6*a[0]*PW2(b[0])*c[2]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[2])*d[0]+(3*a[0]*PW2(b[0])*PW2(c[2])+6*a[0]*PW2(b[0])*c[1]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[1])*d[1]+(6*a[0]*PW2(b[0])*c[1]*c[2]+6*a[0]*PW2(b[0])*c[0]*c[3]-6*PW2(a[0])*b[0]*c[2]*d[1]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[0]+2*(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*d[0])*d[2]+3*(a[0]*PW2(b[0])*PW2(c[1])+2*a[0]*PW2(b[0])*c[0]*c[2]-2*PW2(a[0])*b[0]*c[2]*d[0]-2*PW2(a[0])*b[0]*c[1]*d[1]+PW3(a[0])*PW2(d[1])-2*(PW2(a[0])*b[0]*c[0]-PW3(a[0])*d[0])*d[2])*d[3];
cf[6]=-PW3(b[0])*PW3(c[2])-3*PW3(b[0])*c[0]*PW2(c[3])-3*PW2(a[0])*b[0]*c[2]*PW2(d[2])+PW3(a[0])*PW3(d[2])+2*(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*c[1]*c[2]-3*(PW2(a[0])*b[0]*c[0]-PW3(a[0])*d[0])*PW2(d[3])-(3*PW2(a[3])*PW3(b[0])-2*a[2]*a[3]*PW2(b[0])*b[1]+2*a[1]*a[3]*b[0]*PW2(b[1])-2*a[0]*a[3]*PW3(b[1])+PW2(a[0])*PW3(b[2])+3*PW2(a[0])*b[0]*PW2(b[3])-(a[0]*a[1]*b[1]-(PW2(a[1])-2*a[0]*a[2])*b[0])*PW2(b[2])+(a[0]*a[2]*PW2(b[1])+(PW2(a[2])-4*a[1]*a[3])*PW2(b[0])-(a[1]*a[2]-6*a[0]*a[3])*b[0]*b[1])*b[2]+(2*a[0]*a[1]*PW2(b[1])+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*b[3])*c[0]-2*(3*PW3(b[0])*c[1]*c[2]-(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*c[0])*c[3]+(PW2(a[0])*a[2]*PW2(b[2])+3*PW3(a[0])*PW2(b[3])+3*a[0]*PW2(b[0])*PW2(c[3])+(PW3(a[2])-3*a[1]*a[2]*a[3]+3*a[0]*PW2(a[3]))*PW2(b[0])-(a[1]*PW2(a[2])-(2*PW2(a[1])+a[0]*a[2])*a[3])*b[0]*b[1]+(a[0]*PW2(a[2])-2*a[0]*a[1]*a[3])*PW2(b[1])+((PW2(a[1])*a[2]-2*a[0]*PW2(a[2])-a[0]*a[1]*a[3])*b[0]-(a[0]*a[1]*a[2]-3*PW2(a[0])*a[3])*b[1])*b[2]-2*(PW2(a[0])*a[1]*b[2]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*b[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[3])*d[0]+(6*a[0]*PW2(b[0])*c[2]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[2])*d[1]+(3*a[0]*PW2(b[0])*PW2(c[2])+6*a[0]*PW2(b[0])*c[1]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[1]+2*(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*d[1])*d[2]+(6*a[0]*PW2(b[0])*c[1]*c[2]+6*a[0]*PW2(b[0])*c[0]*c[3]-6*PW2(a[0])*b[0]*c[2]*d[1]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[0]+2*(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*d[0]-6*(PW2(a[0])*b[0]*c[1]-PW3(a[0])*d[1])*d[2])*d[3];
cf[7]=-3*PW3(b[0])*c[1]*PW2(c[3])+(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*PW2(c[2])+(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*PW2(d[2])-3*(PW2(a[0])*b[0]*c[1]-PW3(a[0])*d[1])*PW2(d[3])-(3*PW2(a[3])*PW3(b[0])-2*a[2]*a[3]*PW2(b[0])*b[1]+2*a[1]*a[3]*b[0]*PW2(b[1])-2*a[0]*a[3]*PW3(b[1])+PW2(a[0])*PW3(b[2])+3*PW2(a[0])*b[0]*PW2(b[3])-(a[0]*a[1]*b[1]-(PW2(a[1])-2*a[0]*a[2])*b[0])*PW2(b[2])+(a[0]*a[2]*PW2(b[1])+(PW2(a[2])-4*a[1]*a[3])*PW2(b[0])-(a[1]*a[2]-6*a[0]*a[3])*b[0]*b[1])*b[2]+(2*a[0]*a[1]*PW2(b[1])+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*b[3])*c[1]-(3*PW3(b[0])*PW2(c[2])-2*(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*c[1])*c[3]+(PW2(a[0])*a[2]*PW2(b[2])+3*PW3(a[0])*PW2(b[3])+3*a[0]*PW2(b[0])*PW2(c[3])+(PW3(a[2])-3*a[1]*a[2]*a[3]+3*a[0]*PW2(a[3]))*PW2(b[0])-(a[1]*PW2(a[2])-(2*PW2(a[1])+a[0]*a[2])*a[3])*b[0]*b[1]+(a[0]*PW2(a[2])-2*a[0]*a[1]*a[3])*PW2(b[1])+((PW2(a[1])*a[2]-2*a[0]*PW2(a[2])-a[0]*a[1]*a[3])*b[0]-(a[0]*a[1]*a[2]-3*PW2(a[0])*a[3])*b[1])*b[2]-2*(PW2(a[0])*a[1]*b[2]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*b[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[3])*d[1]+(6*a[0]*PW2(b[0])*c[2]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[2])*d[2]+(3*a[0]*PW2(b[0])*PW2(c[2])+6*a[0]*PW2(b[0])*c[1]*c[3]-6*PW2(a[0])*b[0]*c[2]*d[2]+3*PW3(a[0])*PW2(d[2])+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[1]+2*(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*d[1])*d[3];
cf[8]=-3*PW3(b[0])*c[2]*PW2(c[3])+2*(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*c[2]*c[3]-3*(PW2(a[0])*b[0]*c[2]-PW3(a[0])*d[2])*PW2(d[3])-(3*PW2(a[3])*PW3(b[0])-2*a[2]*a[3]*PW2(b[0])*b[1]+2*a[1]*a[3]*b[0]*PW2(b[1])-2*a[0]*a[3]*PW3(b[1])+PW2(a[0])*PW3(b[2])+3*PW2(a[0])*b[0]*PW2(b[3])-(a[0]*a[1]*b[1]-(PW2(a[1])-2*a[0]*a[2])*b[0])*PW2(b[2])+(a[0]*a[2]*PW2(b[1])+(PW2(a[2])-4*a[1]*a[3])*PW2(b[0])-(a[1]*a[2]-6*a[0]*a[3])*b[0]*b[1])*b[2]+(2*a[0]*a[1]*PW2(b[1])+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*b[3])*c[2]+(PW2(a[0])*a[2]*PW2(b[2])+3*PW3(a[0])*PW2(b[3])+3*a[0]*PW2(b[0])*PW2(c[3])+(PW3(a[2])-3*a[1]*a[2]*a[3]+3*a[0]*PW2(a[3]))*PW2(b[0])-(a[1]*PW2(a[2])-(2*PW2(a[1])+a[0]*a[2])*a[3])*b[0]*b[1]+(a[0]*PW2(a[2])-2*a[0]*a[1]*a[3])*PW2(b[1])+((PW2(a[1])*a[2]-2*a[0]*PW2(a[2])-a[0]*a[1]*a[3])*b[0]-(a[0]*a[1]*a[2]-3*PW2(a[0])*a[3])*b[1])*b[2]-2*(PW2(a[0])*a[1]*b[2]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*b[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[3])*d[2]+(6*a[0]*PW2(b[0])*c[2]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[2]+2*(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*d[2])*d[3];
cf[9]=PW3(a[3])*PW3(b[0])-a[2]*PW2(a[3])*PW2(b[0])*b[1]+a[1]*PW2(a[3])*b[0]*PW2(b[1])-a[0]*PW2(a[3])*PW3(b[1])+PW2(a[0])*a[3]*PW3(b[2])-PW3(a[0])*PW3(b[3])-PW3(b[0])*PW3(c[3])+PW3(a[0])*PW3(d[3])-(a[0]*a[1]*a[3]*b[1]-(PW2(a[1])-2*a[0]*a[2])*a[3]*b[0])*PW2(b[2])+(PW2(a[0])*a[1]*b[2]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*PW2(b[3])+(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*PW2(c[3])+(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*PW2(d[3])+(a[0]*a[2]*a[3]*PW2(b[1])+(PW2(a[2])*a[3]-2*a[1]*PW2(a[3]))*PW2(b[0])-(a[1]*a[2]*a[3]-3*a[0]*PW2(a[3]))*b[0]*b[1])*b[2]-(PW2(a[0])*a[2]*PW2(b[2])+(PW3(a[2])-3*a[1]*a[2]*a[3]+3*a[0]*PW2(a[3]))*PW2(b[0])-(a[1]*PW2(a[2])-(2*PW2(a[1])+a[0]*a[2])*a[3])*b[0]*b[1]+(a[0]*PW2(a[2])-2*a[0]*a[1]*a[3])*PW2(b[1])+((PW2(a[1])*a[2]-2*a[0]*PW2(a[2])-a[0]*a[1]*a[3])*b[0]-(a[0]*a[1]*a[2]-3*PW2(a[0])*a[3])*b[1])*b[2])*b[3]-(3*PW2(a[3])*PW3(b[0])-2*a[2]*a[3]*PW2(b[0])*b[1]+2*a[1]*a[3]*b[0]*PW2(b[1])-2*a[0]*a[3]*PW3(b[1])+PW2(a[0])*PW3(b[2])+3*PW2(a[0])*b[0]*PW2(b[3])-(a[0]*a[1]*b[1]-(PW2(a[1])-2*a[0]*a[2])*b[0])*PW2(b[2])+(a[0]*a[2]*PW2(b[1])+(PW2(a[2])-4*a[1]*a[3])*PW2(b[0])-(a[1]*a[2]-6*a[0]*a[3])*b[0]*b[1])*b[2]+(2*a[0]*a[1]*PW2(b[1])+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*b[3])*c[3]+(PW2(a[0])*a[2]*PW2(b[2])+3*PW3(a[0])*PW2(b[3])+3*a[0]*PW2(b[0])*PW2(c[3])+(PW3(a[2])-3*a[1]*a[2]*a[3]+3*a[0]*PW2(a[3]))*PW2(b[0])-(a[1]*PW2(a[2])-(2*PW2(a[1])+a[0]*a[2])*a[3])*b[0]*b[1]+(a[0]*PW2(a[2])-2*a[0]*a[1]*a[3])*PW2(b[1])+((PW2(a[1])*a[2]-2*a[0]*PW2(a[2])-a[0]*a[1]*a[3])*b[0]-(a[0]*a[1]*a[2]-3*PW2(a[0])*a[3])*b[1])*b[2]-2*(PW2(a[0])*a[1]*b[2]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*b[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[3])*d[3];
}else if(abs(a[1])>=EZERO||abs(b[1])>=EZERO){
// 曲線0は2次
cf[0]=0;
cf[1]=0;
cf[2]=0;
cf[3]=PW2(b[1])*PW2(c[0])-2*a[1]*b[1]*c[0]*d[0]+PW2(a[1])*PW2(d[0]);
cf[4]=2*PW2(b[1])*c[0]*c[1]-2*a[1]*b[1]*c[1]*d[0]-2*(a[1]*b[1]*c[0]-PW2(a[1])*d[0])*d[1];
cf[5]=PW2(b[1])*PW2(c[1])+2*PW2(b[1])*c[0]*c[2]-2*a[1]*b[1]*c[2]*d[0]-2*a[1]*b[1]*c[1]*d[1]+PW2(a[1])*PW2(d[1])-2*(a[1]*b[1]*c[0]-PW2(a[1])*d[0])*d[2];
cf[6]=2*PW2(b[1])*c[1]*c[2]+2*PW2(b[1])*c[0]*c[3]-2*a[1]*b[1]*c[2]*d[1]-(2*a[3]*PW2(b[1])-a[2]*b[1]*b[2]+a[1]*PW2(b[2])-2*a[1]*b[1]*b[3])*c[0]+(a[1]*a[2]*b[2]-2*PW2(a[1])*b[3]-2*a[1]*b[1]*c[3]-(PW2(a[2])-2*a[1]*a[3])*b[1])*d[0]-2*(a[1]*b[1]*c[1]-PW2(a[1])*d[1])*d[2]-2*(a[1]*b[1]*c[0]-PW2(a[1])*d[0])*d[3];
cf[7]=PW2(b[1])*PW2(c[2])+2*PW2(b[1])*c[1]*c[3]-2*a[1]*b[1]*c[2]*d[2]+PW2(a[1])*PW2(d[2])-(2*a[3]*PW2(b[1])-a[2]*b[1]*b[2]+a[1]*PW2(b[2])-2*a[1]*b[1]*b[3])*c[1]+(a[1]*a[2]*b[2]-2*PW2(a[1])*b[3]-2*a[1]*b[1]*c[3]-(PW2(a[2])-2*a[1]*a[3])*b[1])*d[1]-2*(a[1]*b[1]*c[1]-PW2(a[1])*d[1])*d[3];
cf[8]=2*PW2(b[1])*c[2]*c[3]-(2*a[3]*PW2(b[1])-a[2]*b[1]*b[2]+a[1]*PW2(b[2])-2*a[1]*b[1]*b[3])*c[2]+(a[1]*a[2]*b[2]-2*PW2(a[1])*b[3]-2*a[1]*b[1]*c[3]-(PW2(a[2])-2*a[1]*a[3])*b[1])*d[2]-2*(a[1]*b[1]*c[2]-PW2(a[1])*d[2])*d[3];
cf[9]=PW2(a[3])*PW2(b[1])-a[2]*a[3]*b[1]*b[2]+a[1]*a[3]*PW2(b[2])+PW2(a[1])*PW2(b[3])+PW2(b[1])*PW2(c[3])+PW2(a[1])*PW2(d[3])-(a[1]*a[2]*b[2]-(PW2(a[2])-2*a[1]*a[3])*b[1])*b[3]-(2*a[3]*PW2(b[1])-a[2]*b[1]*b[2]+a[1]*PW2(b[2])-2*a[1]*b[1]*b[3])*c[3]+(a[1]*a[2]*b[2]-2*PW2(a[1])*b[3]-2*a[1]*b[1]*c[3]-(PW2(a[2])-2*a[1]*a[3])*b[1])*d[3];
}else{
// 曲線0は1次
cf[0]=0;
cf[1]=0;
cf[2]=0;
cf[3]=0;
cf[4]=0;
cf[5]=0;
cf[6]=b[2]*c[0]-a[2]*d[0];
cf[7]=b[2]*c[1]-a[2]*d[1];
cf[8]=b[2]*c[2]-a[2]*d[2];
cf[9]=-a[3]*b[2]+a[2]*b[3]+b[2]*c[3]-a[2]*d[3];
}
}
// 3次パラメトリック曲線どうしの交点の陰伏方程式F1(t)の係数を求める
void coefImp1(
double *a, // IN 曲線0 (x,y)=f(t)の係数列 a[0],b[0]が3次項の係数
double *b,
double *c, // IN 曲線1 (x,y)=g(u)の係数列 c[0],d[0]が3次項の係数
double *d,
double *cf) // OUT F1(t)の係数列 cf[0]が9次項の係数
{
if(abs(c[0])>=EZERO||abs(d[0])>=EZERO){
// 曲線1は3次
cf[0]=PW3(b[0])*PW3(c[0])-3*a[0]*PW2(b[0])*PW2(c[0])*d[0]+3*PW2(a[0])*b[0]*c[0]*PW2(d[0])-PW3(a[0])*PW3(d[0]);
cf[1]=3*PW2(b[0])*b[1]*PW3(c[0])-3*PW2(a[0])*a[1]*PW3(d[0])-3*(a[1]*PW2(b[0])+2*a[0]*b[0]*b[1])*PW2(c[0])*d[0]+3*(2*a[0]*a[1]*b[0]+PW2(a[0])*b[1])*c[0]*PW2(d[0]);
cf[2]=3*(b[0]*PW2(b[1])+PW2(b[0])*b[2])*PW3(c[0])-3*(a[2]*PW2(b[0])+2*a[1]*b[0]*b[1]+a[0]*PW2(b[1])+2*a[0]*b[0]*b[2])*PW2(c[0])*d[0]+3*(2*a[0]*a[1]*b[1]+PW2(a[0])*b[2]+(PW2(a[1])+2*a[0]*a[2])*b[0])*c[0]*PW2(d[0])-3*(a[0]*PW2(a[1])+PW2(a[0])*a[2])*PW3(d[0]);
cf[3]=-PW2(a[0])*c[0]*PW3(d[1])+(PW3(b[1])+6*b[0]*b[1]*b[2]+3*PW2(b[0])*b[3])*PW3(c[0])-(PW3(a[1])+6*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3]-3*PW2(a[0])*c[3])*PW3(d[0])+3*(a[0]*b[0]*c[1]*c[2]-2*a[0]*b[0]*c[0]*c[3]+(2*a[0]*a[1]*b[2]+PW2(a[0])*b[3]+2*(a[1]*a[2]+a[0]*a[3])*b[0]+(PW2(a[1])+2*a[0]*a[2])*b[1])*c[0])*PW2(d[0])+(2*a[0]*b[0]*c[0]*c[1]+PW2(a[0])*c[1]*d[0])*PW2(d[1])+(PW2(b[0])*PW3(c[1])-3*PW2(b[0])*c[0]*c[1]*c[2]+3*PW2(b[0])*PW2(c[0])*c[3]-3*(a[3]*PW2(b[0])+2*a[2]*b[0]*b[1]+a[1]*PW2(b[1])+2*a[0]*b[0]*b[3]+2*(a[1]*b[0]+a[0]*b[1])*b[2])*PW2(c[0]))*d[0]-(PW2(b[0])*c[0]*PW2(c[1])-2*PW2(b[0])*PW2(c[0])*c[2]+PW2(a[0])*c[2]*PW2(d[0])+(2*a[0]*b[0]*PW2(c[1])+a[0]*b[0]*c[0]*c[2])*d[0])*d[1]+(PW2(b[0])*PW2(c[0])*c[1]+a[0]*b[0]*c[0]*c[1]*d[0]-2*PW2(a[0])*c[1]*PW2(d[0])-3*(a[0]*b[0]*PW2(c[0])-PW2(a[0])*c[0]*d[0])*d[1])*d[2]-3*(PW2(b[0])*PW3(c[0])-2*a[0]*b[0]*PW2(c[0])*d[0]+PW2(a[0])*c[0]*PW2(d[0]))*d[3];
cf[4]=-2*a[0]*a[1]*c[0]*PW3(d[1])+3*(PW2(b[1])*b[2]+b[0]*PW2(b[2])+2*b[0]*b[1]*b[3])*PW3(c[0])-3*(PW2(a[1])*a[2]+a[0]*PW2(a[2])+2*a[0]*a[1]*a[3]-2*a[0]*a[1]*c[3])*PW3(d[0])+3*((a[1]*b[0]+a[0]*b[1])*c[1]*c[2]-2*(a[1]*b[0]+a[0]*b[1])*c[0]*c[3]+(2*a[0]*a[1]*b[3]+(PW2(a[2])+2*a[1]*a[3])*b[0]+2*(a[1]*a[2]+a[0]*a[3])*b[1]+(PW2(a[1])+2*a[0]*a[2])*b[2])*c[0])*PW2(d[0])+2*(a[0]*a[1]*c[1]*d[0]+(a[1]*b[0]+a[0]*b[1])*c[0]*c[1])*PW2(d[1])+(2*b[0]*b[1]*PW3(c[1])-6*b[0]*b[1]*c[0]*c[1]*c[2]+6*b[0]*b[1]*PW2(c[0])*c[3]-3*(2*a[3]*b[0]*b[1]+a[2]*PW2(b[1])+a[0]*PW2(b[2])+2*(a[2]*b[0]+a[1]*b[1])*b[2]+2*(a[1]*b[0]+a[0]*b[1])*b[3])*PW2(c[0]))*d[0]-(2*b[0]*b[1]*c[0]*PW2(c[1])-4*b[0]*b[1]*PW2(c[0])*c[2]+2*a[0]*a[1]*c[2]*PW2(d[0])+(2*(a[1]*b[0]+a[0]*b[1])*PW2(c[1])+(a[1]*b[0]+a[0]*b[1])*c[0]*c[2])*d[0])*d[1]+(2*b[0]*b[1]*PW2(c[0])*c[1]-4*a[0]*a[1]*c[1]*PW2(d[0])+(a[1]*b[0]+a[0]*b[1])*c[0]*c[1]*d[0]+3*(2*a[0]*a[1]*c[0]*d[0]-(a[1]*b[0]+a[0]*b[1])*PW2(c[0]))*d[1])*d[2]-6*(b[0]*b[1]*PW3(c[0])+a[0]*a[1]*c[0]*PW2(d[0])-(a[1]*b[0]+a[0]*b[1])*PW2(c[0])*d[0])*d[3];
cf[5]=-(PW2(a[1])+2*a[0]*a[2])*c[0]*PW3(d[1])+3*(b[1]*PW2(b[2])+(PW2(b[1])+2*b[0]*b[2])*b[3])*PW3(c[0])-3*(a[1]*PW2(a[2])+(PW2(a[1])+2*a[0]*a[2])*a[3]-(PW2(a[1])+2*a[0]*a[2])*c[3])*PW3(d[0])+3*((a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*c[1]*c[2]-2*(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*c[0]*c[3]+(2*a[2]*a[3]*b[0]+(PW2(a[2])+2*a[1]*a[3])*b[1]+2*(a[1]*a[2]+a[0]*a[3])*b[2]+(PW2(a[1])+2*a[0]*a[2])*b[3])*c[0])*PW2(d[0])+(2*(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*c[0]*c[1]+(PW2(a[1])+2*a[0]*a[2])*c[1]*d[0])*PW2(d[1])+((PW2(b[1])+2*b[0]*b[2])*PW3(c[1])-3*(PW2(b[1])+2*b[0]*b[2])*c[0]*c[1]*c[2]+3*(PW2(b[1])+2*b[0]*b[2])*PW2(c[0])*c[3]-3*(a[3]*PW2(b[1])+a[1]*PW2(b[2])+2*(a[3]*b[0]+a[2]*b[1])*b[2]+2*(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*b[3])*PW2(c[0]))*d[0]-((PW2(b[1])+2*b[0]*b[2])*c[0]*PW2(c[1])-2*(PW2(b[1])+2*b[0]*b[2])*PW2(c[0])*c[2]+(PW2(a[1])+2*a[0]*a[2])*c[2]*PW2(d[0])+(2*(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*PW2(c[1])+(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*c[0]*c[2])*d[0])*d[1]+((PW2(b[1])+2*b[0]*b[2])*PW2(c[0])*c[1]+(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*c[0]*c[1]*d[0]-2*(PW2(a[1])+2*a[0]*a[2])*c[1]*PW2(d[0])-3*((a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*PW2(c[0])-(PW2(a[1])+2*a[0]*a[2])*c[0]*d[0])*d[1])*d[2]-3*((PW2(b[1])+2*b[0]*b[2])*PW3(c[0])-2*(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*PW2(c[0])*d[0]+(PW2(a[1])+2*a[0]*a[2])*c[0]*PW2(d[0]))*d[3];
cf[6]=-a[0]*PW2(c[0])*PW3(d[2])+(PW3(b[2])+6*b[1]*b[2]*b[3]+3*b[0]*PW2(b[3]))*PW3(c[0])-(PW3(a[2])+6*a[1]*a[2]*a[3]+3*a[0]*PW2(a[3])+3*a[0]*PW2(c[3])-6*(a[1]*a[2]+a[0]*a[3])*c[3])*PW3(d[0])+2*(a[0]*c[0]*c[3]-(a[1]*a[2]+a[0]*a[3])*c[0])*PW3(d[1])+(b[0]*PW3(c[2])+3*b[0]*c[0]*PW2(c[3])+3*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*c[1]*c[2]+3*(PW2(a[3])*b[0]+2*a[2]*a[3]*b[1]+(PW2(a[2])+2*a[1]*a[3])*b[2]+2*(a[1]*a[2]+a[0]*a[3])*b[3])*c[0]-3*(b[0]*c[1]*c[2]+2*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*c[0])*c[3])*PW2(d[0])+(b[0]*c[0]*PW2(c[2])-2*b[0]*c[0]*c[1]*c[3]+2*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*c[0]*c[1]-2*(a[0]*c[1]*c[3]-(a[1]*a[2]+a[0]*a[3])*c[1])*d[0])*PW2(d[1])+(b[0]*PW2(c[0])*c[2]+a[0]*c[0]*c[1]*d[1]-(a[0]*PW2(c[1])-2*a[0]*c[0]*c[2])*d[0])*PW2(d[2])+3*(b[0]*PW3(c[0])-a[0]*PW2(c[0])*d[0])*PW2(d[3])+(2*(b[1]*b[2]+b[0]*b[3])*PW3(c[1])-6*(b[1]*b[2]+b[0]*b[3])*c[0]*c[1]*c[2]+6*(b[1]*b[2]+b[0]*b[3])*PW2(c[0])*c[3]-3*(2*a[3]*b[1]*b[2]+a[2]*PW2(b[2])+a[0]*PW2(b[3])+2*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2])*b[3])*PW2(c[0]))*d[0]-(2*(b[1]*b[2]+b[0]*b[3])*c[0]*PW2(c[1])-4*(b[1]*b[2]+b[0]*b[3])*PW2(c[0])*c[2]-2*(a[0]*c[2]*c[3]-(a[1]*a[2]+a[0]*a[3])*c[2])*PW2(d[0])+(b[0]*c[1]*PW2(c[2])+2*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*PW2(c[1])+(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*c[0]*c[2]-(2*b[0]*PW2(c[1])+b[0]*c[0]*c[2])*c[3])*d[0])*d[1]-(a[0]*c[0]*c[2]*PW2(d[1])-2*(b[1]*b[2]+b[0]*b[3])*PW2(c[0])*c[1]+(a[0]*PW2(c[2])-4*a[0]*c[1]*c[3]+4*(a[1]*a[2]+a[0]*a[3])*c[1])*PW2(d[0])-(b[0]*PW2(c[1])*c[2]-2*b[0]*c[0]*PW2(c[2])-b[0]*c[0]*c[1]*c[3]+(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*c[0]*c[1])*d[0]+(b[0]*c[0]*c[1]*c[2]-3*b[0]*PW2(c[0])*c[3]+3*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*PW2(c[0])-(a[0]*c[1]*c[2]-6*a[0]*c[0]*c[3]+6*(a[1]*a[2]+a[0]*a[3])*c[0])*d[0])*d[1])*d[2]-(2*a[0]*c[0]*c[1]*PW2(d[1])+6*(b[1]*b[2]+b[0]*b[3])*PW3(c[0])+3*(a[0]*c[1]*c[2]-2*a[0]*c[0]*c[3]+2*(a[1]*a[2]+a[0]*a[3])*c[0])*PW2(d[0])+2*(b[0]*PW3(c[1])-3*b[0]*c[0]*c[1]*c[2]+3*b[0]*PW2(c[0])*c[3]-3*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*PW2(c[0]))*d[0]-(2*b[0]*c[0]*PW2(c[1])-4*b[0]*PW2(c[0])*c[2]+(2*a[0]*PW2(c[1])+a[0]*c[0]*c[2])*d[0])*d[1]+(2*b[0]*PW2(c[0])*c[1]+a[0]*c[0]*c[1]*d[0]-3*a[0]*PW2(c[0])*d[1])*d[2])*d[3];
cf[7]=-a[1]*PW2(c[0])*PW3(d[2])+3*(PW2(b[2])*b[3]+b[1]*PW2(b[3]))*PW3(c[0])-3*(PW2(a[2])*a[3]+a[1]*PW2(a[3])+a[1]*PW2(c[3])-(PW2(a[2])+2*a[1]*a[3])*c[3])*PW3(d[0])+(2*a[1]*c[0]*c[3]-(PW2(a[2])+2*a[1]*a[3])*c[0])*PW3(d[1])+(b[1]*PW3(c[2])+3*b[1]*c[0]*PW2(c[3])+3*(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*c[1]*c[2]+3*(PW2(a[3])*b[1]+2*a[2]*a[3]*b[2]+(PW2(a[2])+2*a[1]*a[3])*b[3])*c[0]-3*(b[1]*c[1]*c[2]+2*(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*c[0])*c[3])*PW2(d[0])+(b[1]*c[0]*PW2(c[2])-2*b[1]*c[0]*c[1]*c[3]+2*(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*c[0]*c[1]-(2*a[1]*c[1]*c[3]-(PW2(a[2])+2*a[1]*a[3])*c[1])*d[0])*PW2(d[1])+(b[1]*PW2(c[0])*c[2]+a[1]*c[0]*c[1]*d[1]-(a[1]*PW2(c[1])-2*a[1]*c[0]*c[2])*d[0])*PW2(d[2])+3*(b[1]*PW3(c[0])-a[1]*PW2(c[0])*d[0])*PW2(d[3])+((PW2(b[2])+2*b[1]*b[3])*PW3(c[1])-3*(PW2(b[2])+2*b[1]*b[3])*c[0]*c[1]*c[2]+3*(PW2(b[2])+2*b[1]*b[3])*PW2(c[0])*c[3]-3*(a[3]*PW2(b[2])+a[1]*PW2(b[3])+2*(a[3]*b[1]+a[2]*b[2])*b[3])*PW2(c[0]))*d[0]-((PW2(b[2])+2*b[1]*b[3])*c[0]*PW2(c[1])-2*(PW2(b[2])+2*b[1]*b[3])*PW2(c[0])*c[2]-(2*a[1]*c[2]*c[3]-(PW2(a[2])+2*a[1]*a[3])*c[2])*PW2(d[0])+(b[1]*c[1]*PW2(c[2])+2*(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*PW2(c[1])+(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*c[0]*c[2]-(2*b[1]*PW2(c[1])+b[1]*c[0]*c[2])*c[3])*d[0])*d[1]-(a[1]*c[0]*c[2]*PW2(d[1])-(PW2(b[2])+2*b[1]*b[3])*PW2(c[0])*c[1]+(a[1]*PW2(c[2])-4*a[1]*c[1]*c[3]+2*(PW2(a[2])+2*a[1]*a[3])*c[1])*PW2(d[0])-(b[1]*PW2(c[1])*c[2]-2*b[1]*c[0]*PW2(c[2])-b[1]*c[0]*c[1]*c[3]+(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*c[0]*c[1])*d[0]+(b[1]*c[0]*c[1]*c[2]-3*b[1]*PW2(c[0])*c[3]+3*(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*PW2(c[0])-(a[1]*c[1]*c[2]-6*a[1]*c[0]*c[3]+3*(PW2(a[2])+2*a[1]*a[3])*c[0])*d[0])*d[1])*d[2]-(2*a[1]*c[0]*c[1]*PW2(d[1])+3*(PW2(b[2])+2*b[1]*b[3])*PW3(c[0])+3*(a[1]*c[1]*c[2]-2*a[1]*c[0]*c[3]+(PW2(a[2])+2*a[1]*a[3])*c[0])*PW2(d[0])+2*(b[1]*PW3(c[1])-3*b[1]*c[0]*c[1]*c[2]+3*b[1]*PW2(c[0])*c[3]-3*(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*PW2(c[0]))*d[0]-(2*b[1]*c[0]*PW2(c[1])-4*b[1]*PW2(c[0])*c[2]+(2*a[1]*PW2(c[1])+a[1]*c[0]*c[2])*d[0])*d[1]+(2*b[1]*PW2(c[0])*c[1]+a[1]*c[0]*c[1]*d[0]-3*a[1]*PW2(c[0])*d[1])*d[2])*d[3];
cf[8]=3*b[2]*PW2(b[3])*PW3(c[0])-a[2]*PW2(c[0])*PW3(d[2])-3*(a[2]*PW2(a[3])-2*a[2]*a[3]*c[3]+a[2]*PW2(c[3]))*PW3(d[0])-2*(a[2]*a[3]*c[0]-a[2]*c[0]*c[3])*PW3(d[1])+(b[2]*PW3(c[2])+3*b[2]*c[0]*PW2(c[3])+3*(a[3]*b[2]+a[2]*b[3])*c[1]*c[2]+3*(PW2(a[3])*b[2]+2*a[2]*a[3]*b[3])*c[0]-3*(b[2]*c[1]*c[2]+2*(a[3]*b[2]+a[2]*b[3])*c[0])*c[3])*PW2(d[0])+(b[2]*c[0]*PW2(c[2])-2*b[2]*c[0]*c[1]*c[3]+2*(a[3]*b[2]+a[2]*b[3])*c[0]*c[1]+2*(a[2]*a[3]*c[1]-a[2]*c[1]*c[3])*d[0])*PW2(d[1])+(b[2]*PW2(c[0])*c[2]+a[2]*c[0]*c[1]*d[1]-(a[2]*PW2(c[1])-2*a[2]*c[0]*c[2])*d[0])*PW2(d[2])+3*(b[2]*PW3(c[0])-a[2]*PW2(c[0])*d[0])*PW2(d[3])+(2*b[2]*b[3]*PW3(c[1])-6*b[2]*b[3]*c[0]*c[1]*c[2]+6*b[2]*b[3]*PW2(c[0])*c[3]-3*(2*a[3]*b[2]*b[3]+a[2]*PW2(b[3]))*PW2(c[0]))*d[0]-(2*b[2]*b[3]*c[0]*PW2(c[1])-4*b[2]*b[3]*PW2(c[0])*c[2]+2*(a[2]*a[3]*c[2]-a[2]*c[2]*c[3])*PW2(d[0])+(b[2]*c[1]*PW2(c[2])+2*(a[3]*b[2]+a[2]*b[3])*PW2(c[1])+(a[3]*b[2]+a[2]*b[3])*c[0]*c[2]-(2*b[2]*PW2(c[1])+b[2]*c[0]*c[2])*c[3])*d[0])*d[1]+(2*b[2]*b[3]*PW2(c[0])*c[1]-a[2]*c[0]*c[2]*PW2(d[1])-(4*a[2]*a[3]*c[1]+a[2]*PW2(c[2])-4*a[2]*c[1]*c[3])*PW2(d[0])+(b[2]*PW2(c[1])*c[2]-2*b[2]*c[0]*PW2(c[2])-b[2]*c[0]*c[1]*c[3]+(a[3]*b[2]+a[2]*b[3])*c[0]*c[1])*d[0]-(b[2]*c[0]*c[1]*c[2]-3*b[2]*PW2(c[0])*c[3]+3*(a[3]*b[2]+a[2]*b[3])*PW2(c[0])-(6*a[2]*a[3]*c[0]+a[2]*c[1]*c[2]-6*a[2]*c[0]*c[3])*d[0])*d[1])*d[2]-(6*b[2]*b[3]*PW3(c[0])+2*a[2]*c[0]*c[1]*PW2(d[1])+3*(2*a[2]*a[3]*c[0]+a[2]*c[1]*c[2]-2*a[2]*c[0]*c[3])*PW2(d[0])+2*(b[2]*PW3(c[1])-3*b[2]*c[0]*c[1]*c[2]+3*b[2]*PW2(c[0])*c[3]-3*(a[3]*b[2]+a[2]*b[3])*PW2(c[0]))*d[0]-(2*b[2]*c[0]*PW2(c[1])-4*b[2]*PW2(c[0])*c[2]+(2*a[2]*PW2(c[1])+a[2]*c[0]*c[2])*d[0])*d[1]+(2*b[2]*PW2(c[0])*c[1]+a[2]*c[0]*c[1]*d[0]-3*a[2]*PW2(c[0])*d[1])*d[2])*d[3];
cf[9]=PW3(b[3])*PW3(c[0])-PW3(c[0])*PW3(d[3])-(PW3(a[3])-3*PW2(a[3])*c[3]+3*a[3]*PW2(c[3])-PW3(c[3]))*PW3(d[0])-(PW2(a[3])*c[0]-2*a[3]*c[0]*c[3]+c[0]*PW2(c[3]))*PW3(d[1])-(a[3]*PW2(c[0])-PW2(c[0])*c[3])*PW3(d[2])+(3*PW2(a[3])*b[3]*c[0]+3*a[3]*b[3]*c[1]*c[2]+b[3]*PW3(c[2])+3*b[3]*c[0]*PW2(c[3])-3*(2*a[3]*b[3]*c[0]+b[3]*c[1]*c[2])*c[3])*PW2(d[0])+(2*a[3]*b[3]*c[0]*c[1]+b[3]*c[0]*PW2(c[2])-2*b[3]*c[0]*c[1]*c[3]+(PW2(a[3])*c[1]-2*a[3]*c[1]*c[3]+c[1]*PW2(c[3]))*d[0])*PW2(d[1])+(b[3]*PW2(c[0])*c[2]-(a[3]*PW2(c[1])-2*a[3]*c[0]*c[2]-(PW2(c[1])-2*c[0]*c[2])*c[3])*d[0]+(a[3]*c[0]*c[1]-c[0]*c[1]*c[3])*d[1])*PW2(d[2])+(3*b[3]*PW3(c[0])+PW2(c[0])*c[1]*d[2]-(3*a[3]*PW2(c[0])-PW3(c[1])+3*c[0]*c[1]*c[2]-3*PW2(c[0])*c[3])*d[0]-(c[0]*PW2(c[1])-2*PW2(c[0])*c[2])*d[1])*PW2(d[3])-(3*a[3]*PW2(b[3])*PW2(c[0])-PW2(b[3])*PW3(c[1])+3*PW2(b[3])*c[0]*c[1]*c[2]-3*PW2(b[3])*PW2(c[0])*c[3])*d[0]-(PW2(b[3])*c[0]*PW2(c[1])-2*PW2(b[3])*PW2(c[0])*c[2]+(PW2(a[3])*c[2]-2*a[3]*c[2]*c[3]+c[2]*PW2(c[3]))*PW2(d[0])+(2*a[3]*b[3]*PW2(c[1])+a[3]*b[3]*c[0]*c[2]+b[3]*c[1]*PW2(c[2])-(2*b[3]*PW2(c[1])+b[3]*c[0]*c[2])*c[3])*d[0])*d[1]+(PW2(b[3])*PW2(c[0])*c[1]-(2*PW2(a[3])*c[1]+a[3]*PW2(c[2])+2*c[1]*PW2(c[3])-(4*a[3]*c[1]+PW2(c[2]))*c[3])*PW2(d[0])-(a[3]*c[0]*c[2]-c[0]*c[2]*c[3])*PW2(d[1])+(a[3]*b[3]*c[0]*c[1]+b[3]*PW2(c[1])*c[2]-2*b[3]*c[0]*PW2(c[2])-b[3]*c[0]*c[1]*c[3])*d[0]-(3*a[3]*b[3]*PW2(c[0])+b[3]*c[0]*c[1]*c[2]-3*b[3]*PW2(c[0])*c[3]-(3*PW2(a[3])*c[0]+a[3]*c[1]*c[2]+3*c[0]*PW2(c[3])-(6*a[3]*c[0]+c[1]*c[2])*c[3])*d[0])*d[1])*d[2]-(3*PW2(b[3])*PW3(c[0])+PW2(c[0])*c[2]*PW2(d[2])+(3*PW2(a[3])*c[0]+3*a[3]*c[1]*c[2]+PW3(c[2])+3*c[0]*PW2(c[3])-3*(2*a[3]*c[0]+c[1]*c[2])*c[3])*PW2(d[0])+(2*a[3]*c[0]*c[1]+c[0]*PW2(c[2])-2*c[0]*c[1]*c[3])*PW2(d[1])-2*(3*a[3]*b[3]*PW2(c[0])-b[3]*PW3(c[1])+3*b[3]*c[0]*c[1]*c[2]-3*b[3]*PW2(c[0])*c[3])*d[0]-(2*b[3]*c[0]*PW2(c[1])-4*b[3]*PW2(c[0])*c[2]+(2*a[3]*PW2(c[1])+a[3]*c[0]*c[2]+c[1]*PW2(c[2])-(2*PW2(c[1])+c[0]*c[2])*c[3])*d[0])*d[1]+(2*b[3]*PW2(c[0])*c[1]+(a[3]*c[0]*c[1]+PW2(c[1])*c[2]-2*c[0]*PW2(c[2])-c[0]*c[1]*c[3])*d[0]-(3*a[3]*PW2(c[0])+c[0]*c[1]*c[2]-3*PW2(c[0])*c[3])*d[1])*d[2])*d[3];
}else if(abs(c[1])>=EZERO||abs(d[1])>=EZERO){
// 曲線1は2次
cf[0]=0;
cf[1]=0;
cf[2]=0;
cf[3]=PW2(b[0])*PW2(c[1])-2*a[0]*b[0]*c[1]*d[1]+PW2(a[0])*PW2(d[1]);
cf[4]=2*b[0]*b[1]*PW2(c[1])+2*a[0]*a[1]*PW2(d[1])-2*(a[1]*b[0]+a[0]*b[1])*c[1]*d[1];
cf[5]=(PW2(b[1])+2*b[0]*b[2])*PW2(c[1])-2*(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*c[1]*d[1]+(PW2(a[1])+2*a[0]*a[2])*PW2(d[1]);
cf[6]=-a[0]*c[1]*PW2(d[2])+2*(b[1]*b[2]+b[0]*b[3])*PW2(c[1])+2*(a[1]*a[2]+a[0]*a[3]-a[0]*c[3])*PW2(d[1])-(b[0]*PW2(c[2])-2*b[0]*c[1]*c[3]+2*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*c[1])*d[1]+(b[0]*c[1]*c[2]+a[0]*c[2]*d[1])*d[2]-2*(b[0]*PW2(c[1])-a[0]*c[1]*d[1])*d[3];
cf[7]=-a[1]*c[1]*PW2(d[2])+(PW2(b[2])+2*b[1]*b[3])*PW2(c[1])+(PW2(a[2])+2*a[1]*a[3]-2*a[1]*c[3])*PW2(d[1])-(b[1]*PW2(c[2])-2*b[1]*c[1]*c[3]+2*(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*c[1])*d[1]+(b[1]*c[1]*c[2]+a[1]*c[2]*d[1])*d[2]-2*(b[1]*PW2(c[1])-a[1]*c[1]*d[1])*d[3];
cf[8]=2*b[2]*b[3]*PW2(c[1])-a[2]*c[1]*PW2(d[2])+2*(a[2]*a[3]-a[2]*c[3])*PW2(d[1])-(b[2]*PW2(c[2])-2*b[2]*c[1]*c[3]+2*(a[3]*b[2]+a[2]*b[3])*c[1])*d[1]+(b[2]*c[1]*c[2]+a[2]*c[2]*d[1])*d[2]-2*(b[2]*PW2(c[1])-a[2]*c[1]*d[1])*d[3];
cf[9]=PW2(b[3])*PW2(c[1])+PW2(c[1])*PW2(d[3])+(PW2(a[3])-2*a[3]*c[3]+PW2(c[3]))*PW2(d[1])-(a[3]*c[1]-c[1]*c[3])*PW2(d[2])-(2*a[3]*b[3]*c[1]+b[3]*PW2(c[2])-2*b[3]*c[1]*c[3])*d[1]+(b[3]*c[1]*c[2]+(a[3]*c[2]-c[2]*c[3])*d[1])*d[2]-(2*b[3]*PW2(c[1])+c[1]*c[2]*d[2]-(2*a[3]*c[1]+PW2(c[2])-2*c[1]*c[3])*d[1])*d[3];
}else{
// 曲線1は1次
cf[0]=0;
cf[1]=0;
cf[2]=0;
cf[3]=0;
cf[4]=0;
cf[5]=0;
cf[6]=-b[0]*c[2]+a[0]*d[2];
cf[7]=-b[1]*c[2]+a[1]*d[2];
cf[8]=-b[2]*c[2]+a[2]*d[2];
cf[9]=-b[3]*c[2]+(a[3]-c[3])*d[2]+c[2]*d[3];
}
}
// 関数値を求める
double p_(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
double x) // IN x
{
return ((((((((ca[0]*x+ca[1])*x+ca[2])*x+ca[3])*x+ca[4])*x+ca[5])*x+ca[6])*x+ca[7])*x+ca[8])*x+ca[9];
}
// 微分値を求める
double pd(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
double x) // IN x
{
return (((((((9*ca[0]*x+8*ca[1])*x+7*ca[2])*x+6*ca[3])*x+5*ca[4])*x+4*ca[5])*x+3*ca[6])*x+2*ca[7])*x+ca[8];
}
// 係数列の符号変化の回数を求める
int nSignVariation(
double *a, // IN 係数列
int n) // IN 係数列のサイズ-1
{
int rv=0;
int sign=0;
for(int i=0;i<=n;i++){
if((sign==1&&*a<0)||(sign==-1&&*a>0))
++rv;
if(*a>0)
sign=1;
else if(*a<0)
sign=-1;
++a;
}
return rv;
}
// Budanの定理のp(x+1)の係数を求める
void coefBudan(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
double *cb) // OUT p(x+1)の係数列 cb[0]が9次項の係数
{
cb[0]=ca[0];
cb[1]=9*ca[0]+ca[1];
cb[2]=36*ca[0]+8*ca[1]+ca[2];
cb[3]=84*ca[0]+28*ca[1]+7*ca[2]+ca[3];
cb[4]=126*ca[0]+56*ca[1]+21*ca[2]+6*ca[3]+ca[4];
cb[5]=126*ca[0]+70*ca[1]+35*ca[2]+15*ca[3]+5*ca[4]+ca[5];
cb[6]=84*ca[0]+56*ca[1]+35*ca[2]+20*ca[3]+10*ca[4]+4*ca[5]+ca[6];
cb[7]=36*ca[0]+28*ca[1]+21*ca[2]+15*ca[3]+10*ca[4]+6*ca[5]+3*ca[6]+ca[7];
cb[8]=9*ca[0]+8*ca[1]+7*ca[2]+6*ca[3]+5*ca[4]+4*ca[5]+3*ca[6]+2*ca[7]+ca[8];
cb[9]=ca[0]+ca[1]+ca[2]+ca[3]+ca[4]+ca[5]+ca[6]+ca[7]+ca[8]+ca[9];
}
// VAG法の係数を求める
void coefVAG(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
double a, // IN 区間の端点
double b,
double *cv) // OUT VAG係数列 cv[0]が9次項の係数
{
cv[0]=((((((((ca[0]*b+ca[1])*b+ca[2])*b+ca[3])*b+ca[4])*b+ca[5])*b+ca[6])*b+ca[7])*b+ca[8])*b+ca[9];
cv[1]=((((((((9*a*ca[0]+ca[1])*b+8*a*ca[1]+2*ca[2])*b+7*a*ca[2]+3*ca[3])*b+6*a*ca[3]+4*ca[4])*b+5*a*ca[4]+5*ca[5])*b+4*a*ca[5]+6*ca[6])*b+3*a*ca[6]+7*ca[7])*b+2*a*ca[7]+8*ca[8])*b+a*ca[8]+9*ca[9];
cv[2]=((((((((36*a*ca[0]+8*ca[1])*a+ca[2])*b+(28*a*ca[1]+14*ca[2])*a+3*ca[3])*b+(21*a*ca[2]+18*ca[3])*a+6*ca[4])*b+(15*a*ca[3]+20*ca[4])*a+10*ca[5])*b+(10*a*ca[4]+20*ca[5])*a+15*ca[6])*b+(6*a*ca[5]+18*ca[6])*a+21*ca[7])*b+(3*a*ca[6]+14*ca[7])*a+28*ca[8])*b+(a*ca[7]+8*ca[8])*a+36*ca[9];
cv[3]=((((((((84*a*ca[0]+28*ca[1])*a+7*ca[2])*a+ca[3])*b+((56*a*ca[1]+42*ca[2])*a+18*ca[3])*a+4*ca[4])*b+((35*a*ca[2]+45*ca[3])*a+30*ca[4])*a+10*ca[5])*b+((20*a*ca[3]+40*ca[4])*a+40*ca[5])*a+20*ca[6])*b+((10*a*ca[4]+30*ca[5])*a+45*ca[6])*a+35*ca[7])*b+((4*a*ca[5]+18*ca[6])*a+42*ca[7])*a+56*ca[8])*b+((a*ca[6]+7*ca[7])*a+28*ca[8])*a+84*ca[9];
cv[4]=((((((((126*a*ca[0]+56*ca[1])*a+21*ca[2])*a+6*ca[3])*a+ca[4])*b+(((70*a*ca[1]+70*ca[2])*a+45*ca[3])*a+20*ca[4])*a+5*ca[5])*b+(((35*a*ca[2]+60*ca[3])*a+60*ca[4])*a+40*ca[5])*a+15*ca[6])*b+(((15*a*ca[3]+40*ca[4])*a+60*ca[5])*a+60*ca[6])*a+35*ca[7])*b+(((5*a*ca[4]+20*ca[5])*a+45*ca[6])*a+70*ca[7])*a+70*ca[8])*b+(((a*ca[5]+6*ca[6])*a+21*ca[7])*a+56*ca[8])*a+126*ca[9];
cv[5]=((((((((126*ca[0]*b+56*ca[1])*b+21*ca[2])*b+6*ca[3])*b+ca[4])*a+(((70*ca[1]*b+70*ca[2])*b+45*ca[3])*b+20*ca[4])*b+5*ca[5])*a+(((35*ca[2]*b+60*ca[3])*b+60*ca[4])*b+40*ca[5])*b+15*ca[6])*a+(((15*ca[3]*b+40*ca[4])*b+60*ca[5])*b+60*ca[6])*b+35*ca[7])*a+(((5*ca[4]*b+20*ca[5])*b+45*ca[6])*b+70*ca[7])*b+70*ca[8])*a+(((ca[5]*b+6*ca[6])*b+21*ca[7])*b+56*ca[8])*b+126*ca[9];
cv[6]=((((((((84*ca[0]*b+28*ca[1])*b+7*ca[2])*b+ca[3])*a+((56*ca[1]*b+42*ca[2])*b+18*ca[3])*b+4*ca[4])*a+((35*ca[2]*b+45*ca[3])*b+30*ca[4])*b+10*ca[5])*a+((20*ca[3]*b+40*ca[4])*b+40*ca[5])*b+20*ca[6])*a+((10*ca[4]*b+30*ca[5])*b+45*ca[6])*b+35*ca[7])*a+((4*ca[5]*b+18*ca[6])*b+42*ca[7])*b+56*ca[8])*a+((ca[6]*b+7*ca[7])*b+28*ca[8])*b+84*ca[9];
cv[7]=((((((((36*ca[0]*b+8*ca[1])*b+ca[2])*a+(28*ca[1]*b+14*ca[2])*b+3*ca[3])*a+(21*ca[2]*b+18*ca[3])*b+6*ca[4])*a+(15*ca[3]*b+20*ca[4])*b+10*ca[5])*a+(10*ca[4]*b+20*ca[5])*b+15*ca[6])*a+(6*ca[5]*b+18*ca[6])*b+21*ca[7])*a+(3*ca[6]*b+14*ca[7])*b+28*ca[8])*a+(ca[7]*b+8*ca[8])*b+36*ca[9];
cv[8]=((((((((9*ca[0]*b+ca[1])*a+8*ca[1]*b+2*ca[2])*a+7*ca[2]*b+3*ca[3])*a+6*ca[3]*b+4*ca[4])*a+5*ca[4]*b+5*ca[5])*a+4*ca[5]*b+6*ca[6])*a+3*ca[6]*b+7*ca[7])*a+2*ca[7]*b+8*ca[8])*a+ca[8]*b+9*ca[9];
cv[9]=((((((((ca[0]*a+ca[1])*a+ca[2])*a+ca[3])*a+ca[4])*a+ca[5])*a+ca[6])*a+ca[7])*a+ca[8])*a+ca[9];
}
// Budanの定理による実根の有無検定
int vBudan( // RETURN p(x)とp(x+1)の係数の符号変化の数の差
double *ca) // IN 関数の係数列 ca[0]が9次項の係数
{
double cb[10];
coefBudan(ca,cb);
return nSignVariation(ca,9)-nSignVariation(cb,9);
}
// VAG法により実根が1個含まれる区間を求める
// ※注意事項:
// この関数は再起呼び出しされます。
// ABMIN(区間長の最小値)の設定や処理系によってはスタックがオーバーフローする可能性があります。
// 必要に応じスタックサイズを調節するなどしてください。
void vVAG(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
Interval &iv, // IN 対象の区間
vector<Interval> &ov) // OUT 実根が1個含まれる区間
{
Interval nv;
double cv[10];
coefVAG(ca,iv.a,iv.b,cv);
int var=nSignVariation(cv,9);
double m=(iv.a+iv.b)/2;
if(var==0){
return;
}else if(var==1){
nv.a=iv.a;
nv.b=iv.b;
nv.pa=p_(ca,iv.a);
nv.pb=p_(ca,iv.b);
nv.nr=var;
ov.push_back(nv);
return;
}else if(iv.b-iv.a<ABMIN){
// 重根
// 区間をABADJ*2に拡張し、重複数を求める
double a=m-ABADJ;
double b=m+ABADJ;
double pa=p_(ca,a);
double pb=p_(ca,b);
coefVAG(ca,a,b,cv);
var=nSignVariation(cv,9);
nv.a=a;
nv.b=b;
nv.pa=pa;
nv.pb=pb;
nv.nr=var;
ov.push_back(nv);
return;
}
double pm=p_(ca,m);
if(abs(pm)<EZERO){
double a=m-ABADJ;
double b=m+ABADJ;
double pa=p_(ca,a);
double pb=p_(ca,b);
nv.a=iv.a;
nv.b=a;
nv.pa=iv.pa;
nv.pb=pa;
vVAG(ca,nv,ov);
coefVAG(ca,a,b,cv);
var=nSignVariation(cv,9);
nv.nr=var;
if(var==1){
nv.a=nv.b=m;
nv.pa=nv.pb=pm;
}else{
// 重根
nv.a=a;
nv.b=b;
nv.pa=pa;
nv.pb=pb;
}
ov.push_back(nv);
nv.a=b;
nv.b=iv.b;
nv.pa=pb;
nv.pb=iv.pb;
vVAG(ca,nv,ov);
}else{
nv.a=iv.a;
nv.b=m;
nv.pa=iv.pa;
nv.pb=pm;
vVAG(ca,nv,ov);
nv.a=m;
nv.b=iv.b;
nv.pa=pm;
nv.pb=iv.pb;
vVAG(ca,nv,ov);
}
}
// 二分法により実根が1個含まれる区間を1/2に縮小する
void vBisection(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
Interval &v) // IN/OUT 対象の区間
{
double m=(v.a+v.b)/2;
double pm=p_(ca,m);
if(abs(pm)<EZERO){
v.a=v.b=m;
v.pa=v.pb=0.0;
return;
}else if(((v.pa>=EZERO||(abs(v.pa)<EZERO&&pd(ca,v.a)>0.0))&&pm<=-EZERO)||
((v.pa<=-EZERO||(abs(v.pa)<EZERO&&pd(ca,v.a)<0.0))&&pm>=EZERO)){
v.b=m;
v.pb=pm;
}else{
v.a=m;
v.pa=pm;
}
return;
}
// Ridder's法により9次関数の実根を求める
// 出典:Kiusalaas, Jaan (2010). Numerical Methods in Engineering with Python (2nd ed.). Cambridge University Press. pp. 147–148. ISBN 978-0-521-19132-6
double ridder( // RETURN 根の近似値
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
Interval &v, // IN 対象の区間
double tol) // IN 収束判定しきい値
{
double a=v.a;
double b=v.b;
double fa=v.pa;
double fb=v.pb;
if(fa==0.0)
return a;
if(fb==0.0)
return b;
if(fa*fb>0.0){
return nan(""); // root is not bracketed
}
double xOld;
for(int i=0;i<30;i++){
// Compute the improved root x from Ridder's formula
double c=0.5*(a+b);
double fc=p_(ca,c);
double s=sqrt(fc*fc-fa*fb);
if(s==0)
return nan("");
double dx=(c-a)*fc/s;
if(fa-fb<0.0)
dx=-dx;
double x=c+dx;
double fx=p_(ca,x);
// Test for convergence
if(i>0&&abs(x-xOld)<tol)
return x;
xOld=x;
// Re-bracket the root as tightly as possible
if(fc*fx>0.0){
if(fa*fx<0.0){
b=x;
fb=fx;
}else{
a=x;
fa=fx;
}
}else{
a=c;
b=x;
fa=fc;
fb=fx;
}
}
return nan(""); // Too many iterations
}
// 9次関数の区間[0,1}の実根を求める
void vRoots(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
vector<double> &rt) // OUT 実根
{
rt.clear();
Interval iv; // 根を求める区間
iv.a=0.0;
iv.b=1.0;
iv.pa=p_(ca,0.0);
iv.pb=p_(ca,1.0);
vector<Interval> rv; // 1つの根が含まれる区間
rv.reserve(9);
if(abs(iv.pa)<EZERO){
// 始点の関数値が0なので、0を根とする
Interval nv;
nv.a=nv.b=0.0;
nv.pa=nv.pb=iv.pa;
rv.push_back(nv);
}
// {0,1}の実根を求める
int nb=vBudan(ca); // Budanの定理による実根の有無検定
if(nb==1){
// {0,1}に1個の実根がある
rv.push_back(iv);
}else if(nb>=2){
// {0,1}に1個以上の実根がある
vVAG(ca,iv,rv);
}
if(rv.size()==0){
// 交点なし、終了
return;
}
// 二分法により実根が1個含まれる区間を1/8に縮小する
// 重根の場合はスキップ
for(Interval& v:rv){
if(v.nr==1&&v.a<v.b){
vBisection(ca,v);
vBisection(ca,v);
vBisection(ca,v);
}
}
for(Interval& v:rv){
if(v.a==v.b){
rt.push_back(v.a);
}else if(v.nr==1){
// 重複なし Ridder's法により実根を求める
double r=ridder(ca,v,ABMIN);
if(!isnan(r)){
rt.push_back(r);
}
}else{
// 重複あり 区間の中央を根とする
rt.push_back((v.a+v.b)/2);
}
}
}
// 3次ベジェ曲線の交点座標を求める
bool vBezierIntersection( // RETURN true:正常
QList<QPointF> &cp0, // IN 3次ベジェ曲線#0 制御点
QList<QPointF> &cp1, // IN 3次ベジェ曲線#1 制御点
QList<QPointF> &op) // OUT 交点座標
{
op.clear();
if(cp0.size()!=4||cp1.size()!=4)
return false;
// 制御点の正規化座標を求める
QList<QPointF> ncp0;
QList<QPointF> ncp1;
normCP(cp0, cp1, ncp0, ncp1);
// 正規化したベジェ曲線の係数を求める
double na[4],nb[4],nc[4],nd[4];
coefBezier(ncp0,na,nb);
coefBezier(ncp1,nc,nd);
// 交点の陰伏方程式F0(u),F1(t)の係数を求める
double cf0[10],cf1[10];
coefImp0(na,nb,nc,nd,cf0);
coefImp1(na,nb,nc,nd,cf1);
vector<double> rt0,rt1; // 根
rt0.reserve(9);
rt1.reserve(9);
// F0(u),F1(t)の根を求める
vRoots(cf0,rt0);
vRoots(cf1,rt1);
QList<QPointF> nip0,nip1; // 交点候補(正規化座標)
for(double u:rt0)
nip0<<pointBezier(nc,nd,u);
for(double t:rt1)
nip1<<pointBezier(na,nb,t);
// 交点候補の座標を突き合わせる
double c[4],d[4];
coefBezier(cp1,c,d);
int i0=0;
foreach(QPointF p0,nip0){
foreach(QPointF p1,nip1){
double dx=p1.x()-p0.x();
double dy=p1.y()-p0.y();
if(sqrt(PW2(dx)+PW2(dy))<=DSTMIN){
// 交点座標(正規化なし)を出力
op<<pointBezier(c,d,rt0[i0]);
}
}
++i0;
}
return true;
}
F) Qtサンプルアプリ
起動すると冒頭の例3(ただし座標値10倍、上下反転)が表示される。
制御点をドラッグして移動すると曲線が更新され、交点が更新される。
#ifndef MAINWINDOW_H
#define MAINWINDOW_H
#include <QMainWindow>
#include <QMouseEvent>
#include <QGraphicsScene>
#include <QGraphicsItem>
#include "scene.h"
QT_BEGIN_NAMESPACE
namespace Ui { class MainWindow; }
QT_END_NAMESPACE
class MainWindow : public QMainWindow
{
Q_OBJECT
public:
MainWindow(QWidget *parent = nullptr);
~MainWindow();
private slots:
void mouseMove(QGraphicsSceneMouseEvent *mouseEvent);
void mousePress(QGraphicsSceneMouseEvent *mouseEvent);
private:
Scene scene;
QGraphicsEllipseItem *rc0[4];
QGraphicsEllipseItem *rc1[4];
QGraphicsPathItem *ci0;
QGraphicsPathItem *ci1;
QList<QGraphicsEllipseItem *> ri;
QList<QPointF> cp0;
QList<QPointF> cp1;
int scp;
private:
Ui::MainWindow *ui;
};
#endif // MAINWINDOW_H
#include "mainwindow.h"
#include "ui_mainwindow.h"
bool vBezierIntersection(
QList<QPointF> &cp0, // IN 3次ベジェ曲線#0 制御点
QList<QPointF> &cp1, // IN 3次ベジェ曲線#1 制御点
QList<QPointF> &op); // OUT 交点座標
MainWindow::MainWindow(QWidget *parent)
: QMainWindow(parent)
, ui(new Ui::MainWindow)
{
ui->setupUi(this);
scene.setSceneRect(0,0,ui->graphicsView->width()-2,ui->graphicsView->height()-2);
ui->graphicsView->setScene(&scene);
ui->graphicsView->setRenderHint(QPainter::Antialiasing);
// 例3の10倍
cp0<<QPointF(70,80);
cp0<<QPointF(230,200);
cp0<<QPointF(10,10);
cp0<<QPointF(150,110);
cp1<<QPointF(100,110);
cp1<<QPointF(220,50);
cp1<<QPointF(20,200);
cp1<<QPointF(120,70);
for(int i=0;i<4;i++){
rc0[i]=scene.addEllipse(cp0[i].x()-2.5,cp0[i].y()-2.5,5,5,QPen(Qt::blue));
rc1[i]=scene.addEllipse(cp1[i].x()-2.5,cp1[i].y()-2.5,5,5,QPen(Qt::darkGreen));
}
{
QPainterPath curve(cp0[0]);
curve.cubicTo(cp0[1],cp0[2],cp0[3]);
ci0=scene.addPath(curve,QPen(QBrush(Qt::blue),1));
}
{
QPainterPath curve(cp1[0]);
curve.cubicTo(cp1[1],cp1[2],cp1[3]);
ci1=scene.addPath(curve,QPen(QBrush(Qt::darkGreen),1));
}
QList<QPointF> op;
vBezierIntersection(cp0,cp1,op);
foreach (QPointF p,op)
ri<<scene.addEllipse(p.x()-2.5,p.y()-2.5,5,5,QPen(Qt::red),QBrush(Qt::red));
scp=-1;
connect(&scene,SIGNAL(mouseMove(QGraphicsSceneMouseEvent*)),this,SLOT(mouseMove(QGraphicsSceneMouseEvent*)));
connect(&scene,SIGNAL(mousePress(QGraphicsSceneMouseEvent*)),this,SLOT(mousePress(QGraphicsSceneMouseEvent*)));
}
MainWindow::~MainWindow()
{
delete ui;
}
void MainWindow::mouseMove(QGraphicsSceneMouseEvent *mouseEvent)
{
if((mouseEvent->buttons()&Qt::LeftButton)&&scp>=0){
QPointF pos=mouseEvent->scenePos();
if(scp<=3){
cp0[scp]=pos;
rc0[scp]->setRect(pos.x()-2.5,pos.y()-2.5,5,5);
QPainterPath curve(cp0[0]);
curve.cubicTo(cp0[1],cp0[2],cp0[3]);
ci0->setPath(curve);
}else{
cp1[scp-4]=pos;
rc1[scp-4]->setRect(pos.x()-2.5,pos.y()-2.5,5,5);
QPainterPath curve(cp1[0]);
curve.cubicTo(cp1[1],cp1[2],cp1[3]);
ci1->setPath(curve);
}
foreach(QGraphicsEllipseItem *gi,ri){
scene.removeItem(gi);
delete gi;
}
ri.clear();
QList<QPointF> op;
vBezierIntersection(cp0,cp1,op);
foreach(QPointF p,op)
ri<<scene.addEllipse(p.x()-2.5,p.y()-2.5,5,5,QPen(Qt::red),QBrush(Qt::red));
}
}
void MainWindow::mousePress(QGraphicsSceneMouseEvent *mouseEvent)
{
if(mouseEvent->buttons() & Qt::LeftButton){
QPointF pos = mouseEvent->scenePos();
scp=-1;
for(int i=0;i<4;i++){
if(QLineF(pos,rc0[i]->rect().center()).length()<=5)
scp=i;
}
for(int i=0;i<4;i++){
if(QLineF(pos,rc1[i]->rect().center()).length()<=5)
scp=i+4;
}
}
}
#ifndef SCENE_H
#define SCENE_H
#include <QObject>
#include <QGraphicsScene>
#include <QGraphicsSceneMouseEvent>
class Scene : public QGraphicsScene
{
Q_OBJECT
public:
explicit Scene(QObject *parent = nullptr);
signals:
void mouseMove(QGraphicsSceneMouseEvent *mouseEvent);
void mousePress(QGraphicsSceneMouseEvent *mouseEvent);
protected:
virtual void mouseMoveEvent(QGraphicsSceneMouseEvent *mouseEvent) override;
virtual void mousePressEvent(QGraphicsSceneMouseEvent *mouseEvent) override;
};
#endif // SCENE_H
#include "scene.h"
Scene::Scene(QObject *parent)
: QGraphicsScene{parent}
{
}
void Scene::mouseMoveEvent(QGraphicsSceneMouseEvent *mouseEvent)
{
emit mouseMove(mouseEvent);
}
void Scene::mousePressEvent(QGraphicsSceneMouseEvent *mouseEvent)
{
emit mousePress(mouseEvent);
}
<?xml version="1.0" encoding="UTF-8"?>
<ui version="4.0">
<class>MainWindow</class>
<widget class="QMainWindow" name="MainWindow">
<property name="geometry">
<rect>
<x>0</x>
<y>0</y>
<width>261</width>
<height>261</height>
</rect>
</property>
<property name="windowTitle">
<string>MainWindow</string>
</property>
<widget class="QWidget" name="centralwidget">
<widget class="QGraphicsView" name="graphicsView">
<property name="geometry">
<rect>
<x>10</x>
<y>10</y>
<width>241</width>
<height>241</height>
</rect>
</property>
<property name="minimumSize">
<size>
<width>100</width>
<height>100</height>
</size>
</property>
<property name="mouseTracking">
<bool>true</bool>
</property>
<property name="alignment">
<set>Qt::AlignmentFlag::AlignLeading|Qt::AlignmentFlag::AlignLeft|Qt::AlignmentFlag::AlignTop</set>
</property>
</widget>
</widget>
</widget>
<resources/>
<connections/>
</ui>
関連記事






