この記事は,以下の論文の解説です.
Bridging the Gap Between Value and Policy Based Reinforcement Learning (NIPS 2017)
記事内容では,強化学習の基礎的な知識を前提としています.
また,記事中の図は全て論文からの引用です.
不備がございましたら,ご指摘頂けると幸いです.
概要
この論文は,エントロピー制約付きの目的関数に関する整合性を用いることで,関数近似のもとでも安定で,かつサンプル効率の良い手法を提案した論文です.(整合性とは,任意の状態行動系列(軌跡)について成り立つ性質のことを指します.例としてはベルマン方程式などがあります.)
一般的にモデルフリーの強化学習は,方策ベースと価値ベースの2つに分類することができます.
方策ベース(e.g. SARSA)の最大の利点は,目的関数を直接最大化することで,関数近似のもとでも安定して学習可能であることです.しかし,一般的に方策を更新するたびに集めたサンプルを捨てる,on-policyのアルゴリズムであるため,サンプル効率が悪いという欠点があります.
価値ベース(e.g. Q学習)では,過去のサンプルも利用可能なoff-policyのアルゴリズムであるため,サンプル効率が良いという利点があります.しかし,関数近似のもとで学習が不安定になりやすく,ハイパーパラメータに鋭敏であるという欠点があります.
この論文では,方策ベースの安定性と価値ベースのサンプル効率の両方を兼ね備えたアルゴリズムを提案します.
- まず,エントロピー制約付きの目的関数のもとで,最適方策と最適価値関数の間の整合性を導出します.
- 次に,その整合性を用いて,安定かつoff policyのActor-Criticの手法 PCL を提案し,さらにActorとCriticを1つのモデルで表現する手法 Unified PCL を提案します.
- その後,トイタスクにおいて,提案手法の優位性について検証します.
準備
以下の議論はすべて確率的なMDPでも成り立ちますが,簡単のため,決定的なダイナミクスを持つMDPを考えます.すなわち,状態 $s_t$ で行動 $a_t$ を行うと,次の状態 $s_{t+1}=f(s_t)$ と報酬 $r_t=r(s_t,a_t)$ が一意に決定されると考えます.また,パラメータ $\theta$ で表現した方策を $\pi_\theta(a|s)$ と表します.
ある状態 $s$ において,方策 $\pi$ に従った時の期待収益は,以下のように再帰的に表すことができます.
O_{ER}(s,\pi) = \sum_a\pi(a|s)[r(s,a)+\gamma O_{ER}(s', \pi)],\;\; s' = f(s,a)
ここで,最適方策 $\pi^{\circ}$ に従ったときの期待収益を最適状態価値 $V^{\circ}(s) = \max_\pi O_{ER}(s,\pi)$ と定義します.よって,最適方策は $\pi^{\circ}=arg\max_\pi O_{ER}(s,\pi)$ と表すことができます.最適方策は,期待収益を最大化する行動確率が1,その他の行動確率が0となるような貪欲方策で表すことができるので,以下の式で表されるhard-maxな整合性を得ることができます.
V^{\circ}(s)=Q_{ER}(s,\pi^{\circ})=\max_a(r(s,a) + \gamma V^{\circ}(s'))
同様の式を,状態行動価値についても導くことができます.
Q^{\circ}(s,a) = r(s,a) + \gamma \max_{a'} Q(s',a')
この式に基づいて価値関数の推定値を更新していく手法を,Q学習と呼びます.これらの整合性には,任意の状態行動系列(軌跡)について成り立つという性質があります.これにより,現在の方策と異なる方策によって収集されたデータでの学習,すなわちoff-policyでの学習が可能になります.
softmaxな整合性
この論文では,エントロピー制約付きの期待収益を目的関数とすることで,softmaxな整合性を導いていきます.
エントロピー制約つきの期待収益を,以下の式で表します.ただし,$\tau$ は制約の強さを表す温度パラメータで,$\mathbb H(a|s)$ は割引累積エントロピーです.
O_{ENT}(s,\pi) = O_{ER}(s,\pi) + \tau \mathbb H(s,\pi)
割引累積エントロピーは,期待収益と同様に以下のように再帰的に表すことができます.
\mathbb H(s,\pi) = \sum_a\pi(a|s)[-\log\pi(a|s) + \gamma \mathbb H(s'|\pi)]
よって,エントロピー制約つきの期待収益は,以下のように表せます.
O_{ENT}(s,\pi) = \sum_a\pi(a|s)[r(s,a) - \tau\log \pi(a|s) +\gamma O_{ENT}(s',\pi)]
ここで,$V^{*}(s)=\max_{\pi} O_{ENT}(s,\pi)$ を(エントロピー制約付きの)最適状態価値とよび,$O_{ENT}$ を最大化する方策 $\pi^{*}$ を最適方策とします.$\tau > 0$ のとき,エントロピー項が方策のエントロピー増加を促進するので,最適方策はもはや決定的な方策ではなく,確率的な方策となります.この最適方策は,以下の式で表すことができます.
\pi^{*}(a|s) \propto \exp\{\frac{r(s,a) + \gamma V^{*}(s')}{\tau}\}
以下に僕なりの導出を示しておきます.
(導出)
最適価値関数は,エントロピー制約つき期待収益 $O_{ENT}$ の方策に関する最大値で表せるので,以下のように式変形できる.
\begin{align} V^{*}(s) &= \sum_a \pi^{*}(a|s) \left(r(s,a)+\gamma V^{*}(s) - \tau \log \pi^{*}(a|s)\right) \\ &=-\tau \sum_a \pi^{*}(a|s) \left( \log\pi^{*}(a|s) - (r(s,a) + \gamma V^{*}(s)) \right) \\ &= -\tau \sum_a \pi^{*}(a|s) \left( \log \frac{\pi^{*}(a|s)}{\exp \{(r(s,a)+\gamma V^{*}(s) )\:/\:\tau\}} \right) \\ &= -\tau \sum_a \pi^{*}(a|s) \left( \log \frac{\pi^{*}(a|s)}{\frac{\exp \{(r(s,a)+\gamma V^{*}(s) )\:/\:\tau\}}{\sum_{a'}\exp \{(r(s,a')+\gamma V^{*}(s) )\:/\:\tau\}}}\right) + \tau\log\sum_{a'} \exp \{(r(s,a')+\gamma V^{*}(s) \} \end{align}
2項目は方策に依存しないので定数とみなす.1項目はKLダイバージェンスの形になっているので,この項を最大化する方策 $\pi^{*}$ は,$\pi^{*} \propto \exp \{(r(s,a)+\gamma V^{*}(s) ) ; / ; \tau\}$ で表すことができる.
この最適方策を,もとのエントロピー制約つきの期待収益の式に代入することで,最適状態価値は以下のようにlog-sum-expの形で表すことができます.
V^*(s) = O_{ENT}(s,\pi^{*}) = \tau\log \sum_a \exp\{\frac{r(s,a)+\gamma V^{*}(s')}{\tau}\}
状態行動価値についても,同様のsoftmaxな整合性を導くことができます.
Q^{*}(s,a) = r(s,a) + \gamma V^{*}(s) = r(s,a) + \gamma \tau\log \sum_{a'} \exp\{\frac{Q^{*}(s',a')}{\tau}\}
この式は,hard-maxな整合性と同様に任意の状態行動系列について成り立つので,この式を元にQ学習に似たoff-policyな学習手法を考えることができます.
(注: Max-Entropy強化学習の文脈やこの論文内では,エントロピー制約付きの期待収益最大化のもとでの最適状態価値を,soft optimal state valueと呼んでいます.この記事では,簡単のため最適状態価値と呼んでいます.)
最適価値と最適方策の整合性
ここでは,最適状態価値 $V^{*}(s)$ と最適方策 $\pi^{*}$ の間の関係性について説明していきます.
まず,最適方策の正規化定数は $\sum_{a'}\exp\{(r(s,a')+\gamma V^{*}(s)) ; / ; \tau \} = \exp\{V^{*}(s) ;/;\tau\}$ となることに注意すると,最適方策は以下の式で表されます.
\pi^{*}(a|s) = \frac{\exp \{(r(s,a')+\gamma V^{*}(s)) \:/\: \tau \}}{\exp\{V^{*}(s) \:/\:\tau\}}
両辺の対数をとって式変形を行うことで,最適状態価値と最適方策に関する整合性を導くことができます.
定理1
任意の $\tau>0, s \in \mathcal S, a\in \mathcal A$ について,最適状態価値 $V^{*}$ と最適方策 $\pi^{*}$ の間に以下の整合性が成り立つ.ただし,$s'=f(s,a)$ とする.
V^{*}(s) - \gamma V^{*}(s') = r(s,a) - \tau \log\pi^{*}(a|s)
最適方策 $\pi^{*}$ は最適な状態行動価値 $Q^{*}(s,a)$ を用いて,以下のように表すこともできます(代入するだけで導出できます).
\pi^{*}(a|s) = \exp \{ (Q^{*}(s,a)-V^{*}(s)) \:/\:\tau\}
また,最適状態価値と最適方策の間には,複数ステップにおける整合性を示すこともできます.
系2
任意の $\tau>0, s_1 \in \mathcal S$ について,最適状態価値 $V^{*}$ と最適方策 $\pi^{*}$ の間に以下の複数ステップの整合性が成り立つ.ただし,$s_{i+1}=f(s_i,a_i)$ とする.
V^{*}(s_1)-\gamma^{t-1} V^{*}(s_t) = \sum_{i=1}^{t-1}\gamma^{i-1}[r(s_i,a_i)-\tau\log\pi^*(a_i|s_i)]
定理1や系2の逆もまた成り立ちます.
定理3
もしある方策 $\pi(a|s)$ と 価値関数 $V(s)$ がすべての$s\in \mathcal S,a\in \mathcal A$ について定理1(または系2)の整合性を満たすのであれば,$\pi=\pi^{*},;V=V^{*}$ である.
この定理3から,1ステップ/複数ステップの整合性の式の両辺の差分を最小化することで,off-policyの強化学習を行うことができると考えられます.
Path Consistency Learning(PCL)
PCL
上で導いた最適状態価値と最適方策の整合性を用いて,パラメータ $\theta$ で表された方策 $\pi_\theta(a|s)$ とパラメータ $\phi$ で表された状態価値 $V_\phi(s)$ の2つのモデルを最適化することを考えます.
ます,長さ $d$ の軌跡 $s_{i:i+d}=(s_i,a_i,\cdots,s_{i+d})$ を用いた整合性を $\theta$ と $\phi$ の関数として定義します.
C(s_{i:i+d},\theta,\phi) =- V_\phi(s_i)+\gamma^dV_\phi(s_{i+d}) + \sum_{j=0}^{d-1}\gamma^j
[r(s_{i+j},a_{i+j})+-\tau \log\pi_\theta(a_{i+j}|s_{i+j})]
任意の軌跡 $s_{i:i+d}$ に関して,上式の $C(s_{i:i+d},\theta,\phi)$ を出来るだけ0に近づけるように $V_\phi$ と $\pi_\theta$ を更新していくことで,off-policyなActor-Criticアルゴリズムを考えることができます.このアルゴリズムを**Path Consistency Learning(PCL)**と呼び,軌跡の集合 $E$ について,$C(s_{i:i+d},\theta,\phi)$ の最小化を行います.
O_{PCL}(\theta,\phi) = \sum_{s_{i:i+d}\in E}\frac{1}{2}C(s_{i:i+d},\theta,\phi)^2
この目的関数の勾配を計算することで,それぞれのパラメータの更新式を以下のように表すことができます.
\begin{align}\Delta \theta&=\eta_\pi C(s_{i:i+d},\theta,\phi) \sum_{j=0}^{d-1}\gamma^j\nabla_\theta\log\pi_\theta(a_{i+j}|s_{i+j}) \\\Delta \phi &=\eta_v C(s_{i:i+d},\theta,\phi) (\nabla_\phi V_\phi(s_i)-\gamma^d\nabla_\phi V_\phi(s_{i+d}))\end{align}
大事なのでもう一度言いますが,定理1,系2は任意の軌跡について成り立つので,上式の更新はoff-policyで行うことが可能です.また,Actor-Criticでは方策を直接目的関数に関して最大化できるため,価値ベースの学習に比べ安定しているという特徴もありました.
実際の実装では,on-policyでの軌跡とリプレイバッファからの軌跡の両方を用いて学習を行っています.詳しい実装に関しては,論文を参照してください.
まとめると,アルゴリズムは以下のようになります.
Unified PCL
PCLでは,方策と状態価値の2つを関数近似しました.しかし,最適状態価値と最適方策の整合性に基づいて,それら2つを1つのモデル,パラメータ $\rho$ で表された状態行動価値 $Q_\rho(s,a)$ で近似することを考えることができます.この状態行動価値を用いると,最適状態価値と最適方策の整合性から,状態価値 $V_\rho(s)$ と方策 $\pi_\rho(a|s)$ は陽に表すことができます.
\begin{align}V_\rho(s) = \tau \log \sum_a\exp\{Q_\rho(s,a) \:/\:\tau\} \\\pi_\rho(a|s)= \exp\{(Q_\rho(s,a)-V_\rho(s)) \:/\:\tau\}\end{align}
状態行動価値 $Q_\rho$ によって表現された状態価値と方策に関して同様の目的関数を考えることで,パラメータ $\rho$ を以下のように更新することができます(導出は, $C^2$ をパラメータ $\rho$ で微分してみてください).
\Delta \rho = \eta_\pi C(s_{i:i+j}, \rho) \sum_{j=0}^{d-1} \gamma^j\nabla\rho\log\pi_\rho(a_{i+j}|s_{i+j}) + \eta_v C(s_{i:i+j}, \rho) (\nabla_\rho V_\rho(s_i)-\gamma^j\nabla_\rho V_\rho(s_{i+d}))
Actor-Critic・Q学習との関係
Advantage Actor-Criticと呼ばれる手法では,方策勾配のベースライン関数として状態価値 $V(s)$ を用いることで方策勾配の推定分散の抑制を行う,on-policyの学習を行います.PCLと同様に,パラメータ $\theta$ で表された方策 $\pi_\theta(a|s)$ とパラメータ $\phi$ で表された状態価値 $V_\phi(s)$ を最適化することを考えます.長さ $d$ の軌跡のアドバンテージ関数の推定 $A(s_{i:i+d},\phi)$ は,以下の式で表すことができます.
A(s_{i:i+d},\phi) = -V_\phi(s_i) + \gamma^d V_\phi(s_{i+d})+ \sum_{j=0}^{d-1}\gamma^jr(s_{i+j},a_{i+j})
パラメータの更新は,以下の式に基づいて行われます.ただし,$s_{i:i+d} | \theta$ は軌跡が現在の方策 $\pi_\theta$ により収集されたことを表します.
\begin{align}\Delta \theta&=\eta_\pi \mathbb E_{s_{i:i+d }| \theta} [A(s_{i:i+d},\phi)\nabla_\theta\log\pi_\theta(a_{i}|s_{i})] \\\Delta \phi &=\eta_v \mathbb E_{s_{i:i+d} | \theta}[A(s_{i:i+d},\phi)\nabla_\phi V_\phi(s_i)]\end{align}
これらの式は,$\tau\to0$ としたときのPCLの更新式に非常に似ています.このことから,PCLはAdvantage Actor-Criticの一般形であるという風に考えることが可能です.ただし,A2CなどのAdvantage Actor-Criticの手法はon-policyなのに対し,PCLはoff-policyなのでサンプル効率の観点では,PCLの方が優位であると言えます.
また,PCLとhard-maxな整合性を用いたQ学習を連想させることもできます.実際に,$d=1$ としたときには,soft Q学習と呼ばれる手法に一致し,Q学習と同様のアルゴリズムを構成することが可能です.
検証
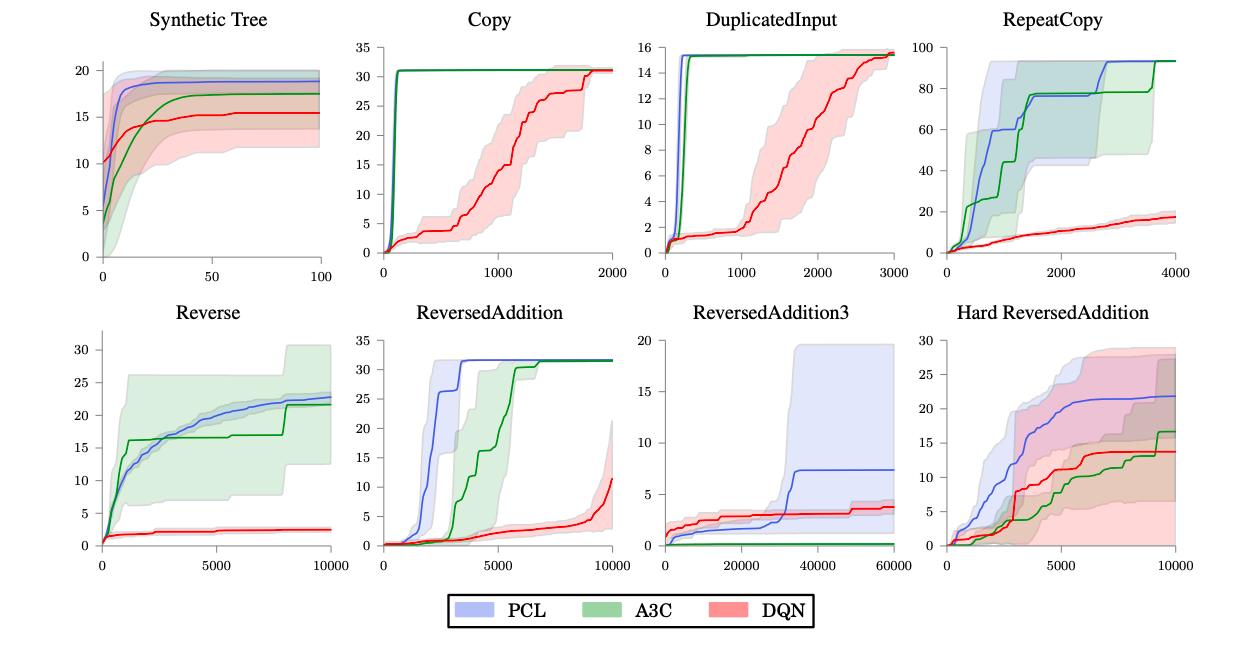
PCL vs A3C, DQN
まず,A3CやDouble DQN+Prioritized Experience Replay(単にDQNと呼びます)とPCLを用いて,複数のトイタスクで検証しています.
上図から,PCLはA3Cなどに比べて優れた性能を示していることがわかります.
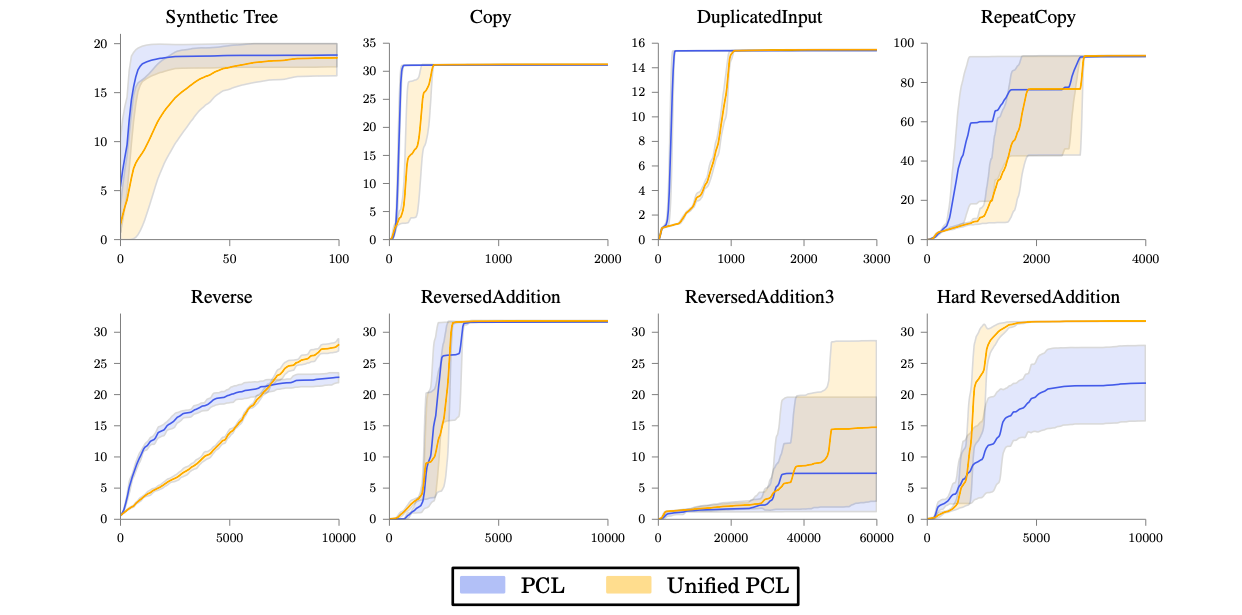
PCL vs Unified PCL
PCLとUnified PCLの比較検証をしています.
上図から,簡単なタスク(e.g. Copy)ではPCLの方が優位なのに対し,難しいタスク(e.g.ReversedAddition3)ではUnified PCLの方が優れた性能を示していることがわかります.
まとめ
この論文では,方策ベースの安定性と価値ベースとサンプル効率の両方を兼ね備えた手法,PCLを提案しました.
今回導出したエントロピー制約付きの期待収益に関する整合性は,他の多くの手法(NACやSoft Actor-Critic)の背景と等価な部分が多く,よく出てきます.log-sum-expの部分の導出まで理解しておくと,他の手法の理解の助けになるかもしれません.