データサイエンティスト スキルチェックリストver.3
『データサイエンティスト スキルチェックリストver.3』はデータサイエンティストに必要とされるスキルをチェックリスト化したもので、データサイエンティストに求められるスキルを「ビジネス力」「データサイエンス力」「データエンジニアリング力」の3分野に分けて定義したものです。
本記事では、データサイエンス力のチェックリストNo.267にある項目について、学んだことをまとめてみます。
| スキルカテゴリ | スキルレベル | サブカテゴリ | チェック項目 |
|---|---|---|---|
| 最適化 | ★★ | 最適化 | 連続最適化問題(制約なし)において、使用可能なアルゴリズムを説明することができる(ニュートン法、最急降下法など) |
チートシート
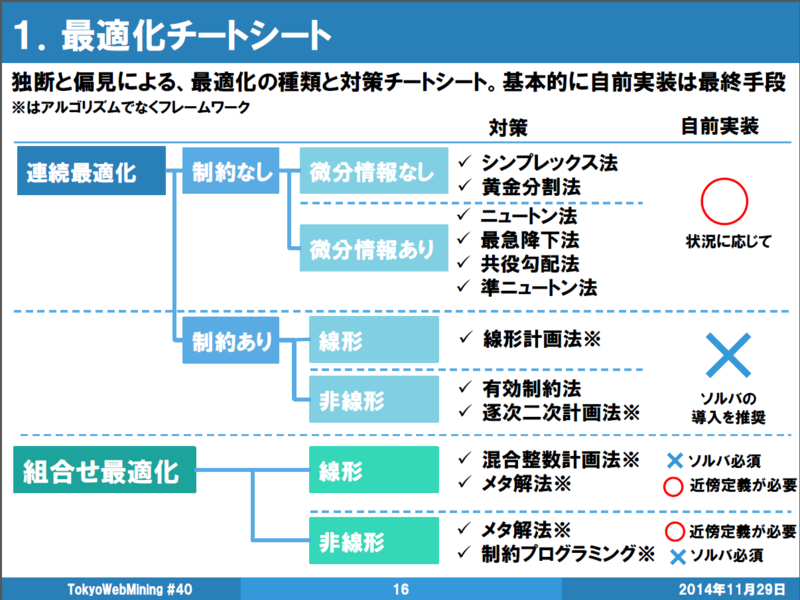
下記に最適化超入門にて紹介されていた最適化チートシートを示します。
本記事では、連続最適化→制約なしについて紹介していきます。
特に、本記事では、微分情報ありについて紹介をしていきます。
連続最適化
連続最適化問題とは、制約条件の集合Aがユークリッド空間 $\mathbb{R}^{n}$ の部分集合の物。
無制約問題を解析的に解く場合は、最適性の必要条件(偏微分を取って 0 )を満たす点の中に最小解がある。
制約条件がある場合はラグランジュの未定乗数法が使える。
(参考:最適化問題)
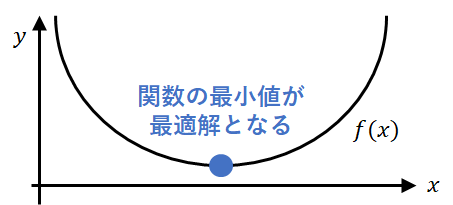
制約なし
制約なしの最適化問題とは、何らかの関数を最小化(もしくは最大化)する問題のことを指します。
\min f(x)
ここで、$f(x)$を目的関数と言います。
上の記述は最小化ですが、最大化の場合でも$f(x)$にマイナスをかけることで最小化に変換できるので最小化のみを考えます。
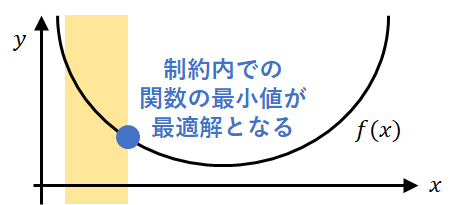
制約あり
制約ありの最適化問題とは、制約下で何らかの関数を最小化(もしくは最大化)する問題のことを指します。
\begin{align}
\min &\ \ f(x) \\
s.t. &\ \ g_i(x) \leq 0 \ \ (i=1,...,m) \\
&\ \ h_j(x) = 0 \ \ (j=1,...,l)
\end{align}
$g_i(x)$、$h_j(x)$を制約関数と呼びます。
さらに、$g_i(x)$, $h_j(x)$はそれぞれ不等式制約、等式制約と呼びます。。
解を求めるための基本的な考え方
反復法
反復法では、適当な初期点$x_0 \in \mathbb{R}^{n}$からスタートして点を更新していきます。
x_{k+1} =x_k+ \alpha_k d_k
ここで$d_k \in \mathbb{R}^{n}$は探索方向と呼ばれ、より最適解に近づくような方向になることが望ましいです。
$\alpha_k \in \mathbb{R}$はステップ幅と呼ばれ、どれぐらい進むかを制御します。
この更新を繰り返したとき、十分小さい$\epsilon$に対して
\left| x_{k+1} - x_k \right| \leq \epsilon
となったときに更新を終了します。これ以上更新を繰り返してもあまり解が変わらないだろうと言えるからです。
探索方向について
探索方向$d_k$は関数の値が減少する方向と一致することが望ましいです。
つまり、以下のような$d_k$が望ましいです。
f(x_{k+1})−f(x_k)=f(x_k+ \alpha_k d_k)−f(x_k) < 0
これから紹介する連続最適化のアルゴリズムは、この$d_k$の決め方が異なります。
ステップ幅について
ステップ幅の決め方としては、Armijo条件(アルミホ条件)とWolfe条件(ウルフ条件)が有名です。
Wolfe条件は、Armijo条件と曲率条件を合わせたものになります。
それぞれ以下で簡単に紹介します。
Armijo条件
探索方向$d_k$が決まっている場合、ある$0<c_1<1$に対して$\alpha_k$がArmijo条件を満たすのは、以下の不等式を満たしていることです。
f(x_k + \alpha_k d_k) \leq f(x_k)+ c_1 \alpha_k \nabla f(x_k) \cdot d_k
$c_1=1$のとき右辺は接線となり、$c_1=0$のとき$y=f(x_k)$に平行な線となります。
つまり、$c_1$は関数の値がどれくらい減って欲しいかのパラメータ(大きいほどたくさん減ってほしい)であり、それに応じた$\alpha_k$が決定されます。
『$\alpha_k$が大きい割に、そこまで関数の値が減らないのはダメ。その2つのバランスは取ろう』という条件になります。
曲率条件
探索方向$d_k$が決まっている場合、ある$c_1<c_2<1$に対して$\alpha_k$が曲率条件を満たすのは、以下の不等式を満たしていることです。
(※$c_1$はArmijo条件で用いたパラメータ)
c_2 \nabla f(c_k) \cdot d_k \leq \nabla f(x_k+\alpha_k d_k) \cdot d_k
Armijo条件は『ステップ幅を大きく取るなら、その分、関数の値も減少させてね』という条件でした。
これを満たそうとすると、ステップ幅を小さく設定することになり、値の更新がなかなか進まなくなります。
そこで、解では勾配$\nabla f(x)$が$0$になることを考え、『次のステップでの勾配が今の勾配よりも緩やかになってほしい(0に近づいてほしい)』という条件を加えます。
これが曲率条件であり、$c_2$は勾配がどれくらい緩やかになればよいかというパラメータです。
アルゴリズム
ここからは、探索方向$d_k$を決めるアルゴリズムについて紹介していきます。
最急降下法
最急降下法では微分方向が探索方向になっている基本的なアルゴリズムです。
すなわち、以下のような探索方向になります。
d_k = − \nabla f(x_k)
さて、簡単に導入をします。
関数$f(x)$を$x_k$周りにテイラー展開して、一次の項まで残すと、以下のようになります。
f(x) \simeq f(x_k) + \nabla f(x_k) (x-x_k)
つまり、最急降下法とは、今いる$x_k$の周りで$f(x)$を1次多項式に近似し、一番急な方向$−\nabla f(x_k)$を探索方向として選んだものになります。
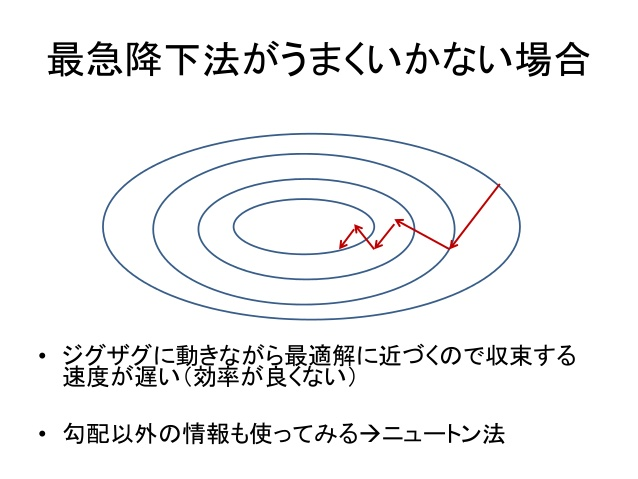
ただし、最急降下法では今いる点の勾配しか見ておらず、ジグザグ走行のようになり、結果的に収束が遅くなる場合があります。
参考:[https://www.slideshare.net/hirsoshnakagawa3/opt-algorithm1](クラシックな機械学習の入門 6. 最適化と学習アルゴリズム)のp.19から引用
ニュートン法
最急降下法では、ジグザクに探索をするため、収束が遅くなる場合があると述べました。
そうした場合、$−\nabla f(x)$が急に変化しない方向を選ぶことで、ジグザクした探索を避けることができ、なめらかに収束が行われるだろう、と思うのは自然な発想でしょう。
さらに、このような発想の場合、$−\nabla f(x)$の変化、すなわち$−\nabla^2 f(x)$を用いるのも自然でしょう。
この$−\nabla^2 f(x_k)$を用いた探索方向を決めるアルゴリズムの一つがニュートン法です。
ニュートン法では、探索方向は以下のように表されます。
d_k = − (\nabla^2 f(x_k))^{-1} \nabla f(x_k)
さて、簡単に導入をします。
最急降下法では一次の項までテイラー展開をしましたが、今度は二次の項まで残します。
\begin{align}
f(x) &\simeq f(x_k) + \nabla f(x_k) (x-x_k) + \frac{1}{2} \nabla^2 f(x_k) (x-x_k)^2 \\
&= \frac{1}{2} \nabla^2 f(x_k) \left\{ (x-x_k)^2 + 2 \nabla^2 f(x_k)^{-1} \nabla f(x_k) (x-x_k) \right\} + f(x_k) \\
&= \frac{1}{2} \nabla^2 f(x_k) \left\{ (x-x_k) + \nabla^2 f(x_k)^{-1} \nabla f(x_k) \right\}^2 - (\nabla^2 f(x_k)^{-1} \nabla f(x_k))^2 + f(x_k)
\end{align}
となるため、$x-x_k=-(\nabla^2 f(x_k))^{-1} \nabla f(x_k)$のときに最小になります。
つまり、二次の項まで考慮した時、これが、関数が最小化される方向になります。
したがってニュートン法では、この右辺を探索方向として採用しています。
しかし、ニュートン法では$\nabla^2 f(x_k)$の計算と、$\nabla^2 f(x_k))^{-1} \nabla f(x_k)$の計算に、とてもコストが掛かることが欠点になります。