目次
- Lassoとは
- Lassoの実装
- 制約の強さを変化させる
- 係数の大きさを図示
- おまけ
参考文献
Lassoとは
Lassoは、線形モデルによる回帰の一つ。
通常最小二乗法と同じ点
- 予測に用いられる式である
通常最小二乗法との異なる点
- リッジ回帰と同様に、係数($w$)が0になるように制約をかける
リッジ回帰と異なる点
- 正則化には、L1正則化が用いられる
- L1正則化を使うと完全に0になる係数がある
- 使われない特徴量が決まり、モデルが解釈しやすくなる
準備
$ pip install scikit-learn
$ pip install mglearn
Lassoの実装
import mglearn
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
lasso = Lasso().fit(X_train, y_train)
print(f"training dataに対しての精度: {lasso.score(X_train, y_train):.2}")
print(f"test set scoreに対しての精度: {lasso.score(X_test, y_test):.2f}")
# => training dataに対しての精度: 0.29
# => test set scoreに対しての精度: 0.21
考察
- training dataへの精度が悪い
- test dataへの精度が悪い
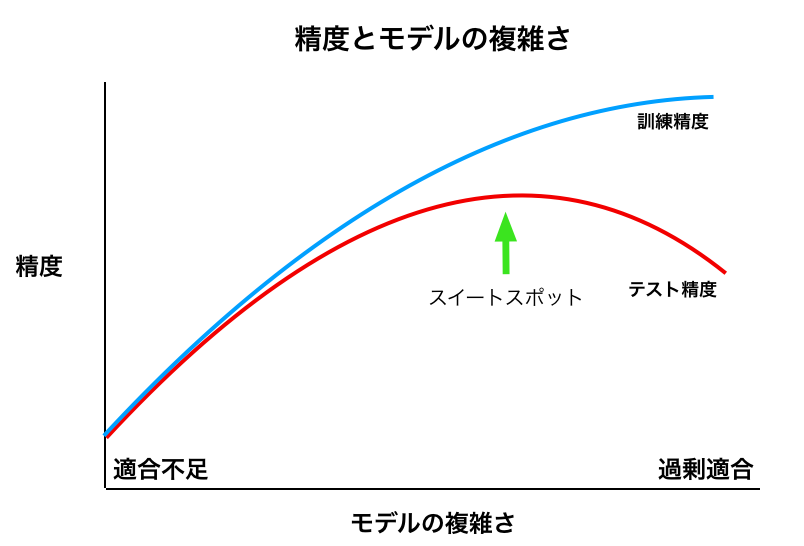
- 適合不足だと考えられる
適合度が低いので、モデルが簡潔すぎるかもしれません。
使われている特徴量の数を確認してみましょう。
import numpy as np
print(f"使われている特徴量の数: {np.sum(lasso.coef_ != 0)}")
# => 使われている特徴量の数: 4
4つしか使われていないようです。
モデルをより複雑にできれば、より精度を上げることができそうです。
Lassoの正則化を調整するには、モデルの引数である alphaを変化させればよい。
制約の強さを変化させる
上のLasspの実装では、正則化の強さは、デフォルト値のままである。
正則化の強弱、つまり、モデルの複雑さは、alphaの値を変化させることにより、僕ら(モデルを構築する側)が決められる。
- alphaを増やす -> 正則化が強くなる -> モデルは簡潔になる
- alphaを減らす -> 正則化が弱くなる -> モデルは複雑になる
aplhaを減らす
「alpha=0.01」にする。
lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print(f"training dataに対する精度: {lasso001.score(X_train, y_train):.2f}")
print(f"test dataに対する精度: {lasso001.score(X_test, y_test):.2f}")
print(f"使われている特徴量の数: {np.sum(np.sum(lasso001.coef_ != 0))}")
# => training dataに対する精度: 0.90
# => test dataに対する精度: 0.77
# => 使われている特徴量の数: 33
考察
-
両方のデータに対しての精度が向上した
- より複雑なモデルになっている
- 上の図でいうと、右に遷移している
-
使われている特徴量の数が増えた
リッジ回帰において、同程度の精度を出すには、104の特徴量全てを使ってモデルを構築する必要があった。
なので、このLassoを用いたモデルでは、33の特徴量しか使われていないので、解釈性が増している。
補足: リッジ回帰
今回のデータセットを用いると、下記の条件でリッジ回帰とLassoは、ほぼ同程度の精度である。
- リッジ回帰: alpha=0.1
- Lasso: alpha=0.01
import mglearn
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
ridge = Ridge(alpha=0.1).fit(X_train, y_train)
print(f"training dataに対しての精度: {ridge.score(X_train, y_train):.2}")
print(f"test set scoreに対しての精度: {ridge.score(X_test, y_test):.2f}")
# => training dataに対しての精度: 0.93
# => test set scoreに対しての精度: 0.77
係数の大きさを図示
import matplotlib.pyplot as plt
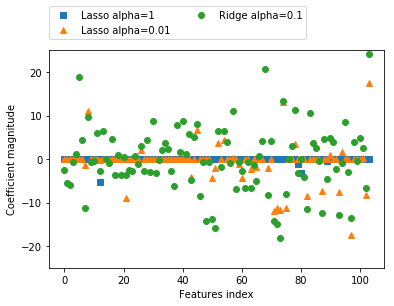
plt.plot(lasso.coef_, 's', label="Lasso alpha=1")
plt.plot(lasso001.coef_, '^', label="Lasso alpha=0.01")
plt.plot(ridge.coef_, 'o', label="Ridge alpha=0.1")
plt.legend(ncol=2, loc=(0, 1.05))
plt.ylim(-25, 25)
plt.xlabel("Features index")
plt.ylabel("Coefficient magnitude")
plt.show()
考察
「リッジ回帰: alpha=0.1」と「Lasso: alpha=0.01」は同程度の精度を示すが、係数のばらつきは「リッジ回帰: alpha=0.1」(緑○)の方がはるかに大きい。
つまり、このモデルを解釈するのは難しい。
よって、解釈性を求められる場合は、Lassoを用いるのが良いだろう。
おまけ
分析結果とグラフとの対応を確認しながら学習すると、理解度が深まると思う。参考書にグラフが出てきた際は、その解説を読む前に、そのグラフを自分なりに読み解いてみると良いかもしれません。