Pythonでリッジ回帰を実装

目次

• リッジ回帰とは
• リッジ回帰の実装
• 制約の強さを変化させる
• おまけ

参考文献

• Pythonではじめる機械学習

リッジ回帰とは

リッジ回帰は、線形モデルによる回帰の一つ。

通常最小二乗法と同じ点

• 予測に用いられる式

通常最小二乗法との異なる点

• 係数($w$)は、訓点データへの予測だけでなく、他の制約へも最適化する
• 個々の特徴量の影響度を小さくしたいため、正則化をする

正則化とは

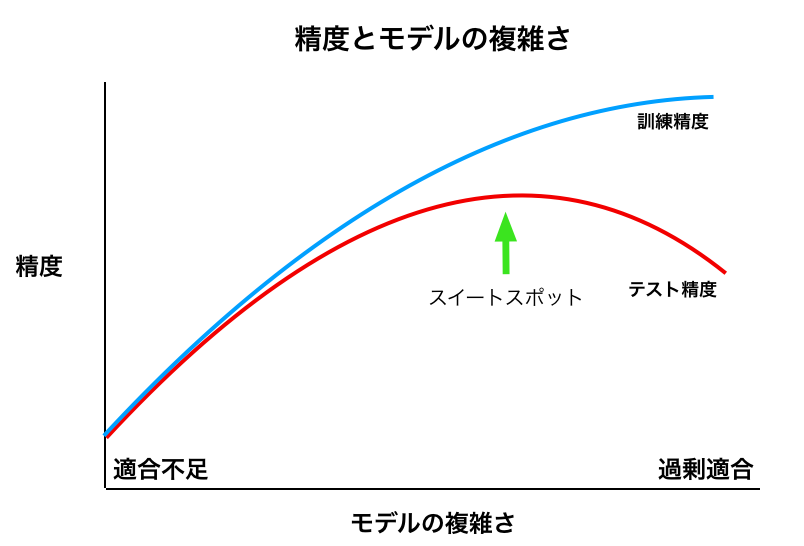
正則化とは、過剰適合(過学習)を防ぐために、モデルが複雑になりすぎないように制約すること。

下の図でいうと、正則化をすることで、左に移動する。

リッジ回帰では、L2正則化が用いられる。

準備

$ pip install scikit-learn
$ pip install mglearn

実装

import mglearn
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split

X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

ridge = Ridge().fit(X_train, y_train)
print(f"training dataに対しての精度: {ridge.score(X_train, y_train):.2}")
print(f"test set scoreに対しての精度: {ridge.score(X_test, y_test):.2f}")
# => training dataに対しての精度: 0.89
# => test set scoreに対しての精度: 0.75

ちなみに同じでデータセットで線形回帰(通常最小二乗法)

from sklearn.linear_model import LinearRegression

X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
lr = LinearRegression().fit(X_train, y_train)
print(f"training dataに対しての精度: {lr.score(X_train, y_train):.2}")
print(f"test dataに対しての精度: {lr.score(X_test, y_test):.2}")
# => training dataに対しての精度: 0.95
# => test dataに対しての精度: 0.61

考察

• リッジ回帰の方がtraining dataへの精度が低い
• リッジ回帰の方がtest dataへの精度が高い
• 過剰適合を防ぎ、モデルの複雑さを軽減できている
  • 予想通り、上の図の左側に遷移したといえる

僕らが目指すのは、test dataに対する精度なので、リッジ回帰の方が良いといえる。

制約の強さを変化させる

上のリッジ回帰の実装では、正則化の強さは、デフォルト値のままである。
正則化の強弱、つまり、モデルの複雑さは、alphaの値を変化させることにより、僕ら(モデルを構築する側)が決められる。

• alphaを増やす　-> 正則化が強くなる -> モデルは簡潔になる
• alphaを減らす　-> 正則化が弱くなる -> モデルは複雑になる

alphaを増やす

「alpha=10」にする。

ridge10 = Ridge(alpha=10).fit(X_train, y_train)
print(f"training dataに対しての精度: {ridge10.score(X_train, y_train):.2}")
print(f"test set scoreに対しての精度: {ridge10.score(X_test, y_test):.2f}")
# => training dataに対しての精度: 0.79
# => test set scoreに対しての精度: 0.64

考察

仮説通り、上の図の左側に遷移し、おそらく「スイートスポット」を超えて、精度が下がった。

aplhaを減らす

「alpha=0.01」にする。

ridge01 = Ridge(alpha=0.1).fit(X_train, y_train)
print(f"training dataに対しての精度: {ridge01.score(X_train, y_train):.2}")
print(f"test set scoreに対しての精度: {ridge01.score(X_test, y_test):.2f}")
# => training dataに対しての精度: 0.93
# => test set scoreに対しての精度: 0.77

考察

仮説通り、上の図の右側に遷移し、おそらく「alpha=1.0」の際より「スイートスポット」に近づき、精度は向上した。
alphaパラメータのモデルへの影響を定量的に知るには、alphaを変化させて、それらのモデルの coef_ 属性を確認するとよいだろう。

だが、本記事ではここまでで、終了して、それらの内容は参考文献で学習してみてください。

おまけ

分析結果とグラフとの対応を確認しながら学習すると、理解度が深まると思う。参考書にグラフが出てきた際は、その解説を読む前に、そのグラフを自分なりに読み解いてみると良いかもしれません。

次の記事では、L1正則化を使うLassoを書きます。