はじめに
@koteko と申します。初めてのアドベントカレンダー参加で緊張しております。
この記事は MATLAB/Simulink Advent Calendar 2020 の 12/10 担当記事です!
前日(12/9)の記事は @yamori813 さんによる「ThingSpeakでInternet of Test」です。
私は数か月ほど前から、研究のためにMATLABを使用する機会がありまして、折角なので何か学びを残そうと思う矢先に、こちらのアドベントカレンダーが企画されていることを知ったため、意を決して参加させていただいた運びとなります。
今回この記事では、「アフィン変換」について書きます。
(数学は専門でないため、厳密であることよりおおよそのイメージを伝えるものであることをご了承ください。)
アフィン変換とは?
1行まとめ
アフィン変換とは、線形変換(回転、拡大縮小、せん断)と平行移動の組み合わせである。
詳解
そもそも「アフィン変換」という言葉に聞き覚えのある方はあまり多くはないでしょう。アフィン変換とは何なのでしょうか?ひとまずwikipediaを見てみましょう。
幾何学におけるアフィン写像(アフィンしゃぞう、英語: affine map)はベクトル空間(厳密にはアフィン空間)の間で定義される、平行移動を伴う線型写像である。アフィン (affine) はラテン語で「類似・関連」を意味する affinis に由来する。
始域と終域が同じであるようなアフィン写像はアフィン変換(アフィンへんかん、英語: affine transformation)と呼ばれる。アフィン写像はアフィン空間の構造を保つ。
何やら小難しいことが書いてあります。わかるようなわからないような…。もう少し見てみましょう。
一般に、アフィン変換は線型変換(回転、拡大縮小、剪断(せん断))と平行移動の組み合わせである。いくつかの線型変換の組合せは一つの線型変換として得られるから、アフィン変換は一般に
$x\mapsto Ax+b$
の形で書けるもので尽くされる。有限次元の場合には、アフィン変換は適当な性質を満たす行列 A とベクトル b を用いて表すことができる。
アフィン変換とは回転、拡大縮小、せん断という線形変換と、平行移動の組み合わせのことのようですね。また、行列を多少知る人にはイメージのしやすいような式が出てきました。
行列を学んだことのある人にとっては、以下の式で2次元座標の回転が行われることはなじみがあると思います。
$$ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} $$
アフィン変換の例としてこうした演算をイメージしてください。
アフィン変換の何が嬉しいか
1行まとめ
線形変換である。(変換が合成できる。)
詳解
前項で軽くスルーしていましたが、
一般に、アフィン変換は線型変換と平行移動の組み合わせである。いくつかの線型変換の組合せは一つの線型変換として得られる...
とあります。線形変換とは何でしょうか?教科書的な定義で行くと
$ V $ と $ W $ とを同じ体 $ 𝔽 $ の上のベクトル空間とする。$ V $ から $ W $ への写像 $ f $ が、任意のベクトル $ x, y ∈ V $ と任意のスカラー $ c ∈ 𝔽 $ に対し、
加法性: $ f(x + y) = f(x) + f(y), $
斉一次性: $ f(cx) = cf (x) $
をともに満たすとき、$ f $ を $ 𝔽 $ 上の線型写像 または簡単に $ 𝔽 $-線型写像という。
という定義がされています。ここでは扱いやすい変換なんだ、というくらいの認識で大丈夫です。
大事なのは線形変換のもつ以下の性質です。
$ f: V → W $ および $ g: W → X $ が線型ならば、その合成 $ g ∘ f $ は $ V $ から $ X $ への線型写像を定める。
一般化されているのでこれだけ読んでもわかりにくいかもしれません。具体的に考えてみましょう。
例えば、2次元空間において「x方向に2倍拡大する」変換 $f$ と「30度回転する」変換 $g$ を考えてみます(これらはアフィン変換です)。
$f$ は座標を座標に移し、$g$ もまた同様です。つまり、$V$だとか$W$だとか$X$とかはすべて同じで、座標(実数空間)です。
このとき、「x方向に2倍拡大し、それから30度回転する」という変換 $g ∘ f$ もまた座標を座標に移す線形変換である、ということです。
これが成り立つということは、「拡大して回転して縮小して…」という変換が「拡大する」「回転する」「縮小する」…といった個別の変換の合成から考えることができるということであり、また、いくらでもつなげられるということを意味します。
**ただし、これらの変換が可換でない(順番を入れ替えたら結果が同じとは限らない)**ことに注意が必要です。これは行列の積が可換でないことからも感じ取れると思います。
まとめると、アフィン変換は線形変換であり、合成が考えられる点が嬉しい点です。
…というのは少し説明不足です。
アフィン変換とは「線型変換と平行移動の組み合わせ」と言っているのだから、平行移動の部分にも触れなければなりません。
わざわざ分けて書かれているように、実は平行移動という操作は線形変換ではありません。
それではアフィン変換も非線形変換なのでは?と思うのが自然ですが、アフィン変換ではこの平行移動を上手く扱って線形性を保った変換になっています。
2次元の例で解説します。
ある点 $(x,y)$ を $(x',y')$ に移す平行移動を伴う変換を表す式は以下のようになります。
$$ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} x_0 \\ y_0 \end{bmatrix} $$
これは連立方程式の形に書き直すと以下のようになります。
$$ x' = a_{11}x + a_{12}y + x_0 \\ y'= a_{21}x + a_{22}y + y_0 $$
ここに余分な次元を追加することで以下のような行列に書き直すことができます。
$$ \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & x_0 \\ a_{21} & a_{22} & y_0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $$
これによって、変換が線形変換とみなせるより大きな空間の部分集合としてもとの空間を考えています。この部分は難しいので、実装上は「平行移動を扱う余分な1次元があるんだな」という点だけ頭に入れておけばよいでしょう。
この概念について、友人に教示してもらった際にわかりやすかった図を以下に引用します。
こういう感じで。 pic.twitter.com/mavA1pzeDH
— Ziphil the Rabicat 🐱🐰 (@Ziphil) November 8, 2020
これはwikipediaでは「アフィン変換の表現」の項でも述べられていることですので、必要に応じて参照してください。
アフィン変換
具体的なコードを提示します。MATLABにおいて、単純なアフィン変換はaffine2dおよびimwarpによって容易に行えます。
img = imread('arrow.png');
% x方向に2倍
mat1=[
2 0 0
0 1 0
0 0 1
];
% y方向に3倍
mat2=[
1 0 0
0 3 0
0 0 1
];
% 60度回転
mat3=[
cosd(60) -sind(60) 0
sind(60) cosd(60) 0
0 0 1
];
matrix=mat1*mat2*mat3;
tform=affine2d(matrix);
img_trans=imwarp(img,tform);
imshowpair(img,img_trans,'blend')
ここで重要なのは3つの変換をかけるのに3回の変換処理(imwarp)が不要であり、各行列の合成を一度かけることによって達成可能という点です。
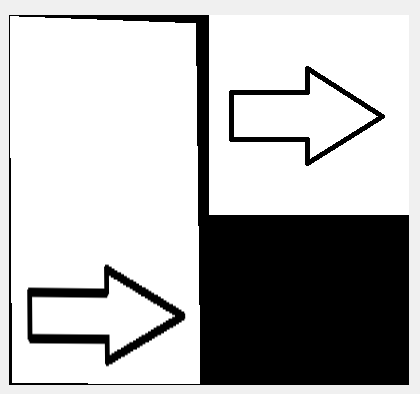
左上に映っているのが元の矢印です。x方向に2倍、y方向に3倍、60度回転した結果が右に表れています。
どのような行列がどのような変換に対応しているかは参考記事に詳しいでしょう。
完全に理解するアフィン変換 - Qiita
変換行列の推定
上記のコードでは、行いたい変換に対して適当な変換行列を決定しましたが、実際に研究を行う場面では、まず適切な変換行列自体を求める必要があることも多いです。
本来同じ角度/位置で得られたデータセットを扱いたいけれど、諸要因によってこれらがずれているため、それらを補正したいという需要があります。(こうした作業をレジストレーションと呼びます)
それらがどれだけずれているか、ということがはっきりしていればすぐに変換行列が定まりますが、このような課題の解決が求められる場面でそのようなことはまずないでしょう。また、いきなり定規と分度器を持ち出してズレをはかるような人もいないでしょう。
そんなことをしなくても、変換行列を求めるための"妥当な"手段が用意されています。そう、MATLABならね。1
強度ベースのレジストレーション
レジストレーションを行う最も直感的なひとつの方法は、強度による位置合わせです。人間は目で見て位置を合わせられますが、コンピュータ上では対象を少しづつずらして差分を計算させるという作業に置き換えられます。MATLABではimregisterという関数が利用できます。MRI画像の研究などで主に用いられます。(すみません、時間がなく参考コードを載せられませんでした。)
コントロールポイントによるレジストレーション
先の強度ベースのレジストレーションは自動推定なのでうまく行かない場合もあります。また、繰り返し演算を行って求める仕組み上処理に時間がかかります。簡便かつ簡明にレジストレーションを行う方法として、いくつかの座標の組から変換行列を決定するという手法があります。基本的な考えとしては座標の組から一般逆行列を最小二乗推定によって導出し、これを変換行列として用いています(解説は省略します)。
(参考:コントロール ポイントを使用した投影歪みのあるイメージのレジストレーション)
% 画像読み込み
img1 = imread('arrow1.png');
img2 = imread('arrow2.png');
% コントロールポイントの設定
[mp,fp] = cpselect(img2,img1,'Wait',true);
% 変換行列の導出
tform=fitgeotrans(mp,fp,'projective');
% レジストレーション
registered=imwarp(img2,tform);
% 結果表示
imshowpair(img1,registered,'montage')
cpselectはGUI上で対話的にコントロールポイントを決定することが出来る関数です。
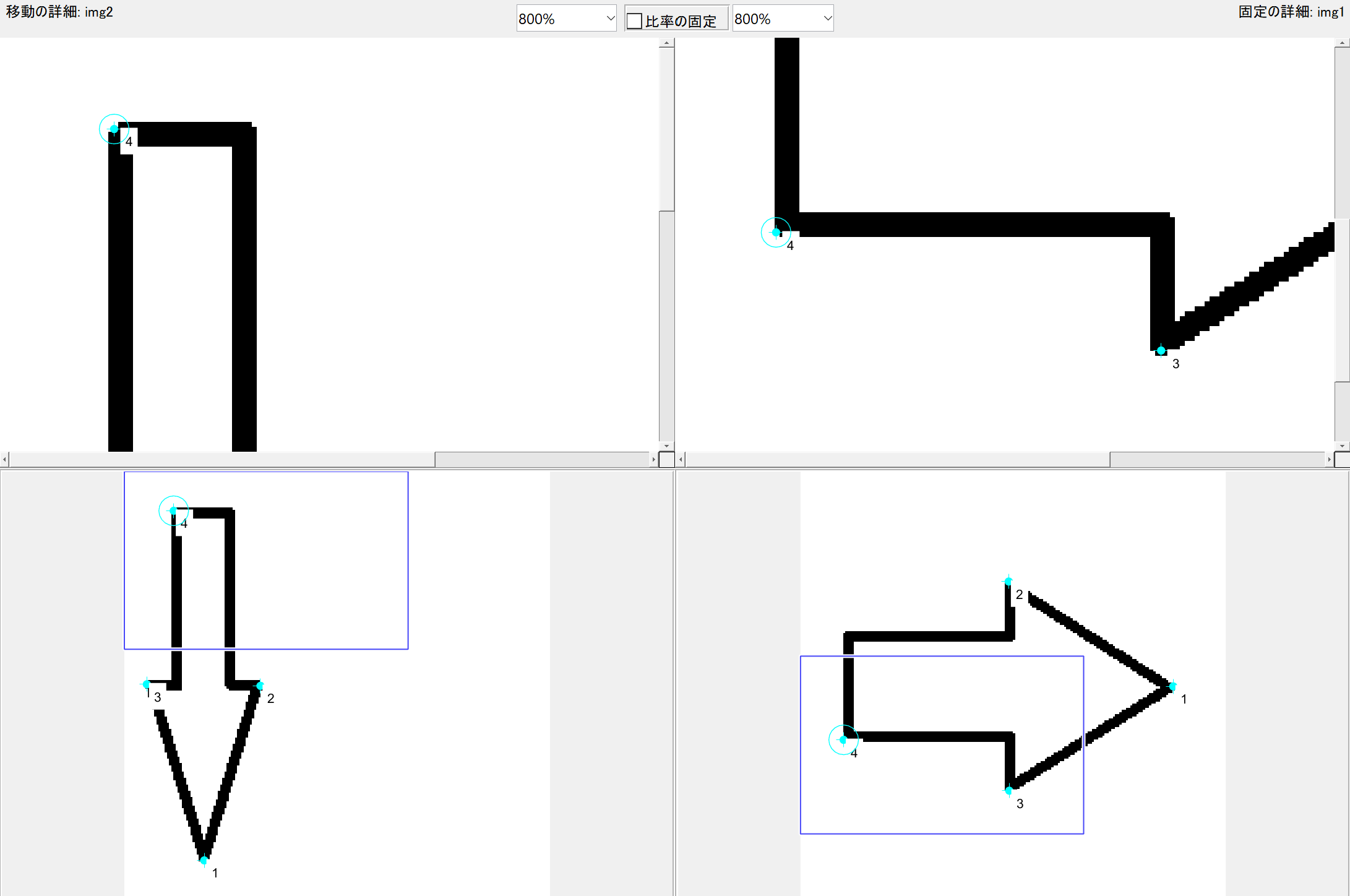
左下の矢印(対象)を右下の矢印に合わせるために4点以上の組を設定します。
推定まとめ
上記で説明した方法などはMTALABのドキュメントにもまとめられています。
2 次元および 3 次元の幾何学的変換プロセスの概要 - MATLAB & Simulink - MathWorks 日本
アフィン変換上での注意
平行移動を含むアフィン変換ついては、参照空間に注意する必要があります。imwarpの引数と出力には参照空間のデータを含むことが出来ます。
img = imread('arrow1.png');
% x,y方向に+500移動
matrix=[
1 0 0
0 1 0
500 500 1
];
ref=imref2d(size(img));
tform=affine2d(matrix);
[img_trans,ref_trans]=imwarp(img,tform);
imshow(img_trans,ref_trans)
※MATLAB上での平行移動項が最後列でなく最下行であることに注意
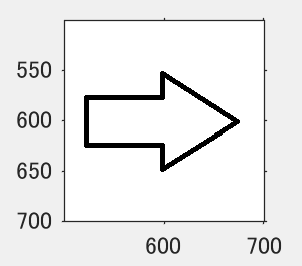
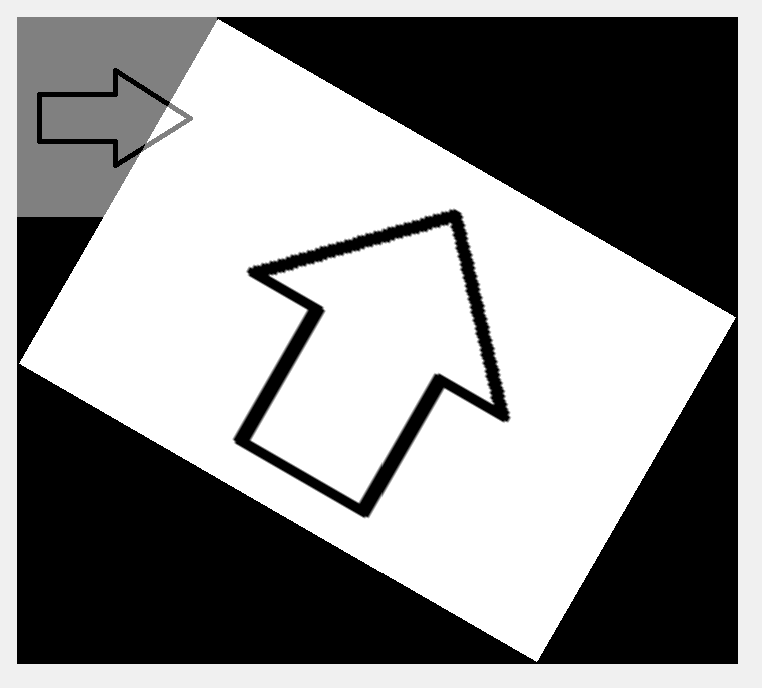
一見すると元の画像と一切変わらないように見えますが、座標軸に注目すると移動していることがわかります。このように、矢印が白背景の中で移動するような動きを期待すると思わぬ結果に見えてしまう可能性があります。画像全体を平行移動しているという点に注意しましょう。
おわりに
5割まで書いた後で当日まで手こずってしまいました…公開が遅くなり申し訳ありません。来年のアドベントカレンダーではもっと余裕をもって書き上げられるよう精進します。
実際の研究での場面をそのまま書くのを避けてやや曖昧な記事になってしまったかもしれませんが、今回初めて本格的にMATLABを触れて色々と勉強になりました。
参考
アフィン写像 - Wikipedia
完全に理解するアフィン変換 - Qiita
2 次元および 3 次元の幾何学的変換プロセスの概要 - MATLAB & Simulink - MathWorks 日本
-
これ書いてる時に知ったんですけど、公式では言ってないらしいです。 ↩