記憶速度の限界による開発リードタイムの数理モデル化

開発速度と記憶速度に関する数理モデル

IPAの資料において、新規開発で書かれるソースコードは1時間当たり6.33行¹だそうです。また、1行当たりの平均文字数を40文字²とします。これはLinuxのコーディング規約が80文字であったため、その値を参考にここでは1行当たり40文字とおいています。

1日に書かれるプログラム情報量I_day^{w}を考えると

\begin{align}
I_{day}^w = 6.33[line/hour] \times 8[hour] \times 40[character/line] 
&= 2025.6[Byte/day] \\
&= 1.9[KByte/day]
\end{align}

ここから平均的な日本のプログラマーは1日当たり、1.9KBの情報量を生成しています。
また、1人月=20日とすると、1か月あたり38KBの情報量を生成します。

以前に人間の記憶速度は7bps未満？という記事を書きました。この中で、人間のt秒後の記憶能力は

I(t) = -28791.2 exp(-1.82 \times 10^{-4}t) + 28791.2[Byte]

という計算を導きました。
しかし、時間が経つと記憶を忘れます。これを生理学的に計算したものにヘルマン・エビングハウスの忘却曲線というものがあります。これによると、1日後には、節約率が34%であるというデータがあります。
ここで"節約率"とは何か。というと、8時間で記憶した内容は、次の日にもう一度覚えなおすときには、34%節約した時間で記憶できる。ということです。したがって、8時間の34%は2.7時間。つまり、ある日に8時間かけて覚えた内容は、次の日に覚えなおすとすると8-2.7=5.3時間かかる。という計算になります。
ここで以下のような立式を行います。

T_i^{new}:i日に新規に記憶する時間 \\
T_i^{rem}:i日に復習に必要な時間 \\
I_i^{new}:i日に新規に記憶する情報量 \\
I_i^{rem}:i日で定着した情報量 \\
I_i^{all}:i日に記憶している情報量 \\
p:1日後の節約率 \\
T:1日の記憶時間

前の節約率の定義により、i+1日に復習に必要な時間は、前日の新規に記憶する時間に依存します。また、新規に記憶する時間は、1日の記憶時間から復習に必要な時間の残りになります。

T_{i+1}^{rem}=T_i^{new}-pT_i^{new} \\
T_{i+1}^{new}=T-T_{i+1}^{rem}

記憶の忘却は、常に起こるものですが、ここではモデルを簡易化し、次の日に復習をすると、完全に記憶出来るものと考えます。そうすることで、i+1日の新規に記憶する時間は、時間の関数として純粋に定義可能で、一方でi+1日で定着した情報量は今までの累計で計算可能です。

I_i^{new} = -28791.2 exp(-1.82 \times 10^{-4} \times T_i^{new}) + 28791.2 \\
I_{i+1}^{rem} = I_i^{new} + I_i^{rem} \\
I_{i}^{all} = I_i^{rem} + I_i^{new}

ここで、初期値として以下の値を用います。

T=28800 \\
p=0.34 \\
T_0^{new} = T

初日はT=28800秒(=8時間)勉強するものとし、忘却曲線の値からp=0.34とします。
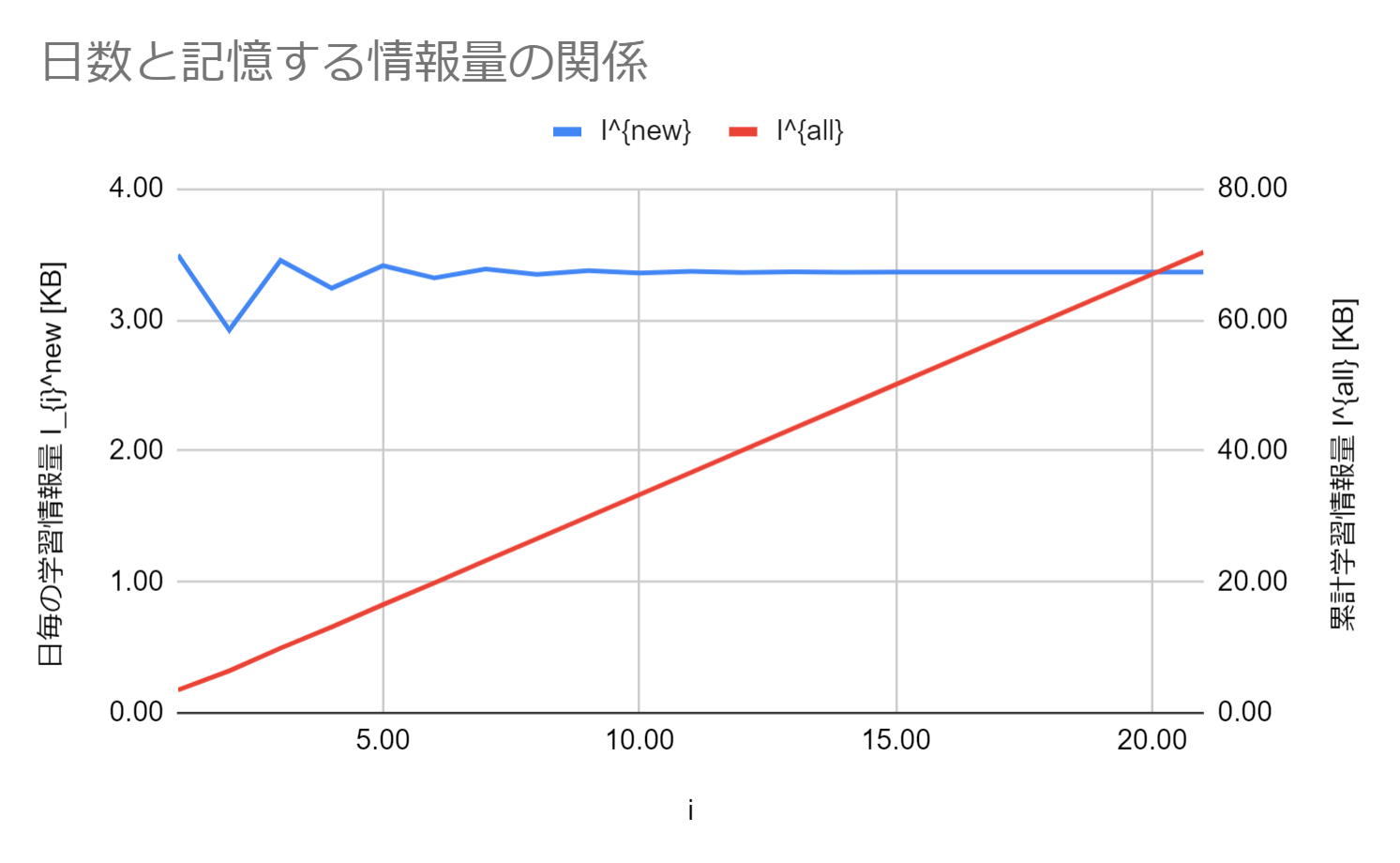
以上の条件より数値計算すると以下の様なグラフを得ます。

グラフを見ることで、記憶をし始めた最初はその記憶量に多少の上下がありますが、日が経つにつれて安定的に記憶できるようになることが分かります。数値的には、1人日あたり3.36KBずつ新規で記憶が可能です。また数値計算の結果から20日、1人月で計算すると66.97KBの記憶が可能です。

開発工数・情報量と記憶にかかる工数の関係

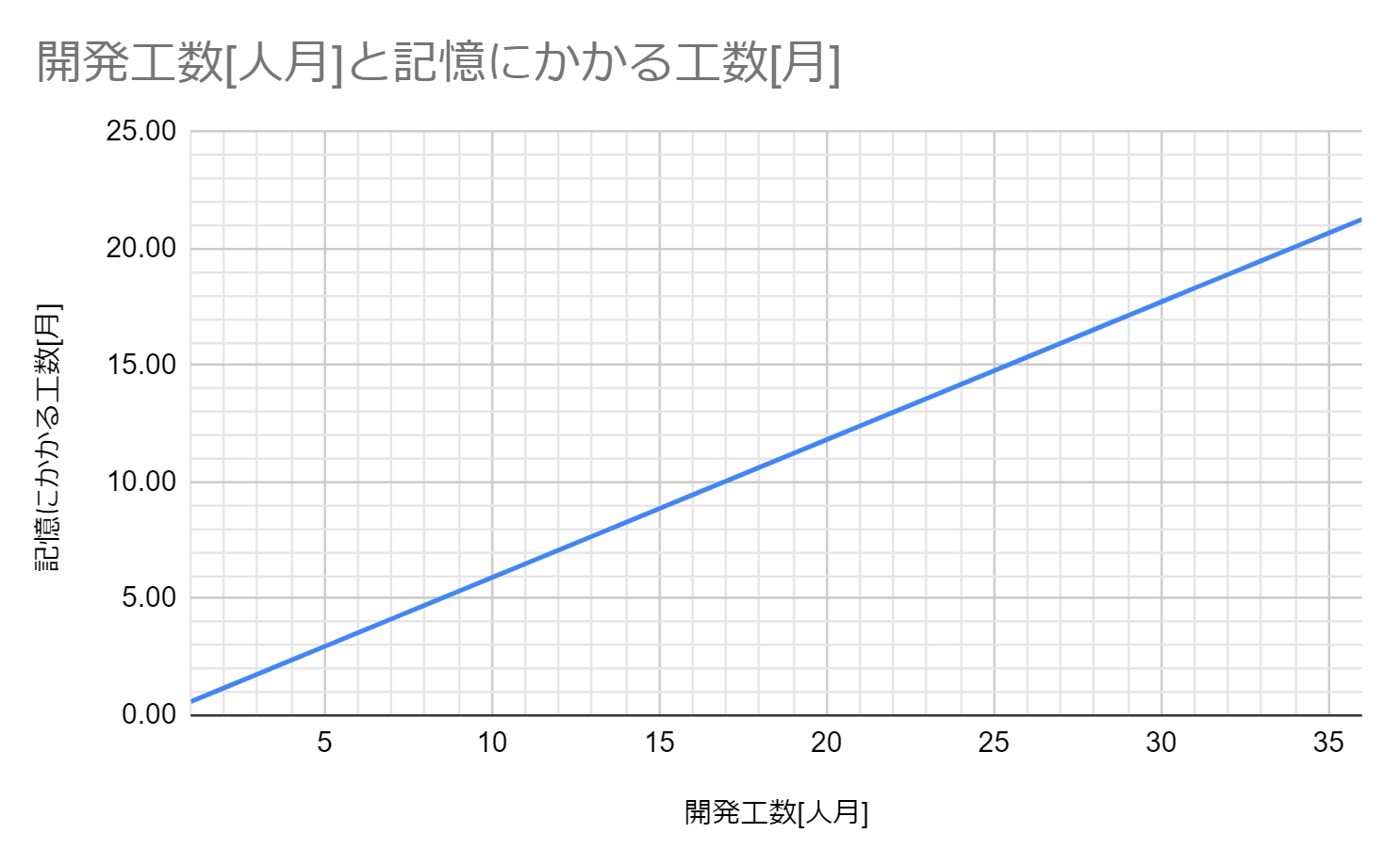
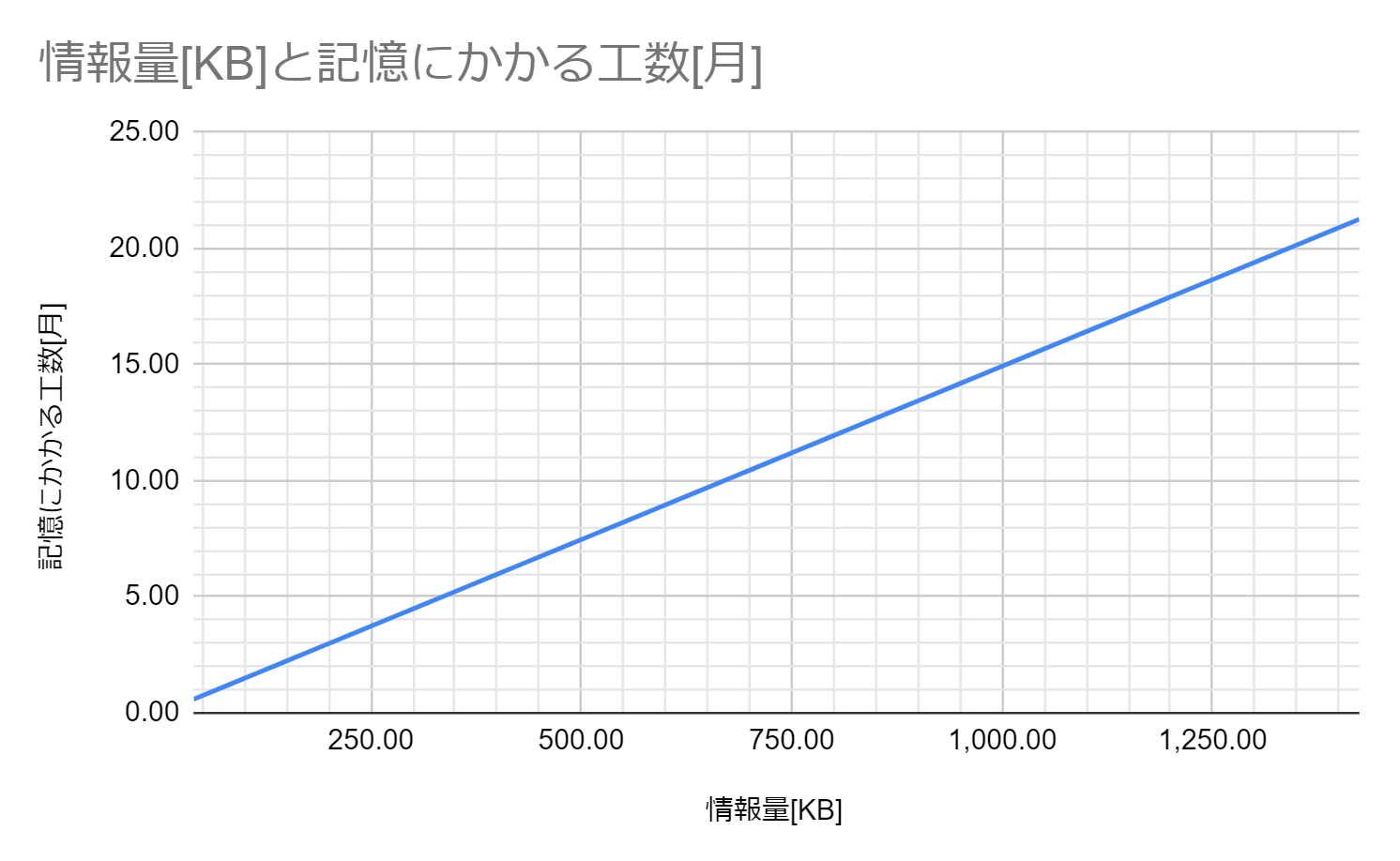
以上の議論をまとめると、1人月の開発で生産される情報量は38KB、1人月で記憶できる情報量は66.97KBだと分かります。これらを用いて、グラフを作成します。

1か月あたり38KBの式をから12人月は474.5KBです。
またSLOCの統計情報から12人月は1.2万行です。
開発に12人月かかったシステムは把握に7人月かかります。
ここで、「まぁそうかもしれないね。」と直感的に思われるかもしれませんが、立式の前提をきちんと見る必要があります。そもそもこれは"ソースコードの記憶のみを毎日8時間し続けて7人月かかる"計算です。何かを他にやりながらではないです。

疎結合・高凝集モジュールの重要性

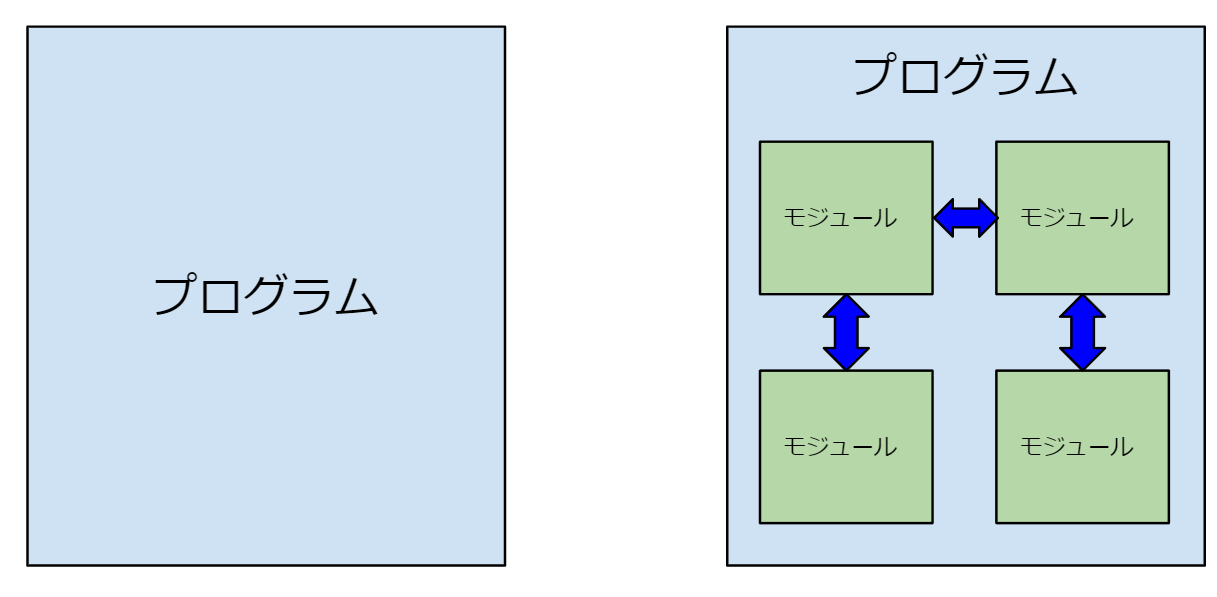
　以上の議論をすると、あまり現実的な解析ではない。という結論に至ると思います。現代的なプログラムは一枚板のプログラムとして作られるわけではなく、いくつかのモジュール(クラスやライブラリ・パッケージ)の組み合わせによって制作されます。したがって、関連するモジュールのみを把握すればよい。という発想は想像に難くないでしょう。

では、本当に疎結合・高凝集で再利用可能なモジュール設計をしているでしょうか？

　ソフトウェアの開発を高速化し、多くの機能をリリースしたい。という圧力は昨今増すばかりです。そういった中で、開発を外注したり、人材会社から派遣社員を雇ったり、短期で開発能力を上げよう。という戦術を取りたくなります。しかし、それは一般論としてうまくいきません。
古典的にはブルックスの法則と呼ばれる法則があります。

1. 新たに投入された開発者が生産性の向上に貢献するまでには、時間がかかる。
2. 人員の投下は、チーム内のコミュニケーションコストを増大させる。
3. タスクの分解可能性には限界がある。

　いわゆるアジャイルの文脈でよく参照されるのは2番です。n人のコミュニケーションを考えた場合、それぞれの人間関係はn*(n-1)/2となります(nC2)。そのため、n^2のオーダーでコミュニケーションが必要になるため、チームの人員が多くなるチームはコミュニケーションコストが高くなり、生産性が上がらない。という理屈です。これはスクラム等で論じられる1チームあたり7±2人にする。というプラクティスを裏付ける内容となります。この人数に関する数理解析は「なぜ、ソフトウェアプロジェクトは人数を増やしても上手くいかないのか」に詳しいです。
　今回、問題にしているのは1.です。では、 仮に人員を投下したとして、開発にコミットするのはどれくらい先か？ を見積もるものです。
　上記の数理解析は端的には開発規模から推定するものです。この解析が現実的ではなく、モジュール化が行われているであろう。という反論はあります。一方で、 そのプログラムのモジュールが疎結合・高凝集な設計で変更の影響が局所化されていなければ、人員の追加しても、ソフトウェアの設計の学習に時間がかかり、開発にコミットできない。 ということが分かります。
　例えば、ソフトウェアを短期で人員を投入して開発完了しました。それらは協力会社の人員にスポットで入ってもらったとします。しかし、再度、人員が必要な開発が始まり、新たな人材を投入すると、システムの学習に時間がかかってしまいます。コミュニケーションだけでなく、学習がリードタイムになり開発が遅れます。また、プログラムの量は確実に増え続けるので、さらに学習に時間がかかります。そして、そのプログラムが疎結合・高凝集になっていないと、さらに学習コストがかかってしまい、さらにリードタイムが長くなります。プロダクトのアジリティを保つためには、その人員は内部で確保するのがベストな戦術になります。
Wikipediaのブルックスの法則では、「遅れているソフトウェアプロジェクトへの要員追加は、プロジェクトをさらに遅らせるだけである」と書かれていますが、まさにその通りの結果を生んでいます。

端的な話をすると

短期の外部の人員投入して期日を早めるような開発ををしてもいいことない

ということです。

• コミュニケーションコストが増える
• 粗悪なコードにより、疎結合・高凝集が崩れ、学習コストが悪化する
• 外部の人員が抜けることで社員が払った教育コストが無駄になる
• 再度、開発リソースが必要になったときには、教育コストが高くなって支払う必要がある
• 教育コストは自社の要員でしか賄えないので、自社の開発工数は他社への回収不能な教育コストで圧迫され、外部人員を投下すればするほど、自社で開発できなくなる。

結局、リードタイムを短く開発し続けるには自社でチームを保持して、学習・教育コストを無駄にせず開発し続けるしかない。という"よくある結論"に落ち着きます。

感想

　すごく雑に話すと、DXやアジャイルの文脈で、「外注するな。内製しろ。」というのはよく聞く言説でした。そして、その理由として、「世の中が目まぐるしく変わる中、リードタイムの長い開発だと世の中のトレンドに追いつけない。そのために、機能を小出しに出来るインクリメンタルな開発をするべきである。そして、インクリメンタルな開発で小出しに機能を出すためには、社内での密なコミュニケーションが必要なので自社で開発組織を作るべきである」という理屈を見ていました。
　しかし、一方で「開発を外注して速度を上げたい。」という気持ちもあるでしょう。そのような方針はなぜダメなのか？ということに関しては理論が弱い印象を受けていました。本文でも書いた、「チームの要員の急激な増加」は「コミュニケーションパスがn^2のオーダーで増えるから」という理屈は端的ですっきりと否定している一方で、「外注することでリードタイムが増加する」というのは、定量的ではなくソフトウェアの外注に関して禁ずる理由付けが曖昧であるという印象を持っていました。
　そんな中で、自分の書いた記事の中で「記憶速度の限界」というものを算定した記事を書きました。そうしたときに、これを「ソフトウェア開発のコードの把握にかかる工数の算定に使えるのではないか？」ということを思いつき、この記事に至りました。
　結果として、「記憶にかかる工数は精緻なものである」とは言えませんが、近似手法としては悪くない手法ではないかと思います。また、本文にも書いた、「現代的なソフトウェア設計ではモジュール分割を行う」ということですが、それは逆説的に、「コードの把握による開発リードタイム削減のためにもモジュール分割をする必要がある」という方針を引き出すことが出来て、「設計は大事」という落としどころにできたので、割と満足しています。
　人間の記憶速度は7bps未満？で書いたように人間の記憶速度に限界があります。そのため、プログラムの内部の把握には時間がかかってしまいます。仮に外注や派遣を用いて人員の増加をしたとしても、中のプログラムの構成が疎結合・高凝集でなければ、学習コストが高く思ったように開発速度は上がりません。しかし、思ったように開発速度が上がらないのは、そもそも内部の構成が悪く、そこに対して端的にお金で解決できるのは人員の投下しかない。というとても辛いジレンマが存在するように思いました。

1. ソフトウェア開発データ白書2018-2019
   図表 8-3-4 ● SLOC 規模別 SLOC 生産性の基本統計量（新規開発）
   https://www.ipa.go.jp/files/000069381.pdf ↩

2. Linuxカーネルのコーディング規約、1行80桁の制限を撤廃
   https://linux.srad.jp/story/20/06/04/1249216/ ↩