メモリースポーツ
メモリースポーツという競技を最近知った。
メモリースポーツは、記憶した能力を披露し競う競技である。Memory Sportsをそのまま直訳し、記憶力競技と呼ばれることもある。イギリス発祥の競技でドイツ、アメリカ、オーストラリア、アルジェリアなど世界40カ国以上で大会が開催されており、英語名ではMemory Championshipと呼ばれ、日本語では記憶力選手権や記憶力大会と呼ばれることが多い。
嵐にしやがれという番組で、1分ほどの時間でトランプの並びを全て覚える映像を見て、こんなことが人間に出来るのか。と驚いた記憶がありました。
その時、このデータから人間の記憶速度の限界って出せるんじゃないか?と思って、計算してみました。
あくまで試算してみる"ネタ"です。空想科学読本の亜種だと思って下さい。
世界記録からの試算
Wikipediaにあるメモリースポーツの世界記録のデータを参考にしました。
| 概要 | 時間(min) | 時間(sec) | 対象 | 記録(桁) | 情報量(bit) | 速度(bps) |
|---|---|---|---|---|---|---|
| 1時間で数字を記憶 | 60 | 3600 | 数字 | 3,238 | 10,756 | 2.99 |
| 30分で数字を記憶 | 30 | 1800 | 数字 | 1,933 | 6,421 | 3.57 |
| 15分で数字を記憶 | 15 | 900 | 数字 | 1,100 | 3,654 | 4.06 |
| 5分で数字を記憶 | 5 | 300 | 数字 | 568 | 1,887 | 6.29 |
| 5分で2進数の並びを記憶 | 5 | 300 | 2進数 | 1,170 | 1,170 | 3.90 |
| 30分で2進数の並びを記憶 | 30 | 1800 | 2進数 | 6,270 | 6,270 | 3.48 |
"2進数の並びを記憶"の情報量は計算がしやすい。0,1の情報量は1bitにあたる。ということは、純粋に桁数=情報量となります。
"数字を記憶"は、10進数である。そのため、n桁の数字の状態の数S_nは、
S_n = 10^n
この情報量I_nは
\begin{align}
I_n &= \log_2 S_n \\
&= \log_2 10^n \\
&= n \log_2 10 \\
I_n &\fallingdotseq 3.32n
\end{align}
10進数のn桁の数字は、大体3.32n[bit]の情報量を持つことが分かります。
これらの情報をグラフにすると以下の様になります。
決定係数が0.98を超える綺麗な線形のグラフになります。そのため、記憶にかける時間と覚えられる情報量は1次式で近似できそうだということが分かります。
また、記憶速度を定義してみます。単純に情報量/時間で計算します。そうすると、 人間の記憶速度は最速でも6.29[bps]だということが分かります。 また、この速度には2.99[bps]から6.29[bps]まである程度のばらつきがみられます。ここで、時間と記憶速度の関係をグラフ化してみます。
そうすると時間とともに記憶の速度が下がっていくことが分かります。
ここで記憶の速度vは
v = 5.24\exp(-1.82 \times 10^{-4}t)
と近似できそうです。これは、人間が疲労し、記憶速度が落ちる。というモデル化と、のちに短期記憶の上限を計算するため、この式で近似しています。
ここで数値を入れてt=0,t=300の範囲で積分します。
\int_{0}^{300}5.24\exp(-1.82 \times 10^{-4}t)dt \fallingdotseq 1529.85
これは300秒間で覚えられる情報量です。表では1,170~1,887[bit]なので、近似精度としては悪くはなさそうです。
また、t=0,t=1の範囲で積分すると
\int_{0}^{1}5.24\exp(-1.82 \times 10^{-4}t)dt \fallingdotseq 5.23952
とでます。記憶速度vは逓減する関数なので、0秒の時が一番記憶速度が速いです。そのため、0~1秒の間が覚えられる速度が一番速くなるはずです。その速度は計算上5.23[bps]のようです。表のデータからも悪くない近似のように思えます。
ここで、vを不定積分します。
\int 5.24\exp(-1.82 \times 10^{-4}t)dt \\
= -28791.2 exp(-1.82 \times 10^{-4}t) + C
t秒後の記憶量I(t)としたとき、I(0)=0なので、
I(t) = -28791.2 exp(-1.82 \times 10^{-4}t) + 28791.2
となります。
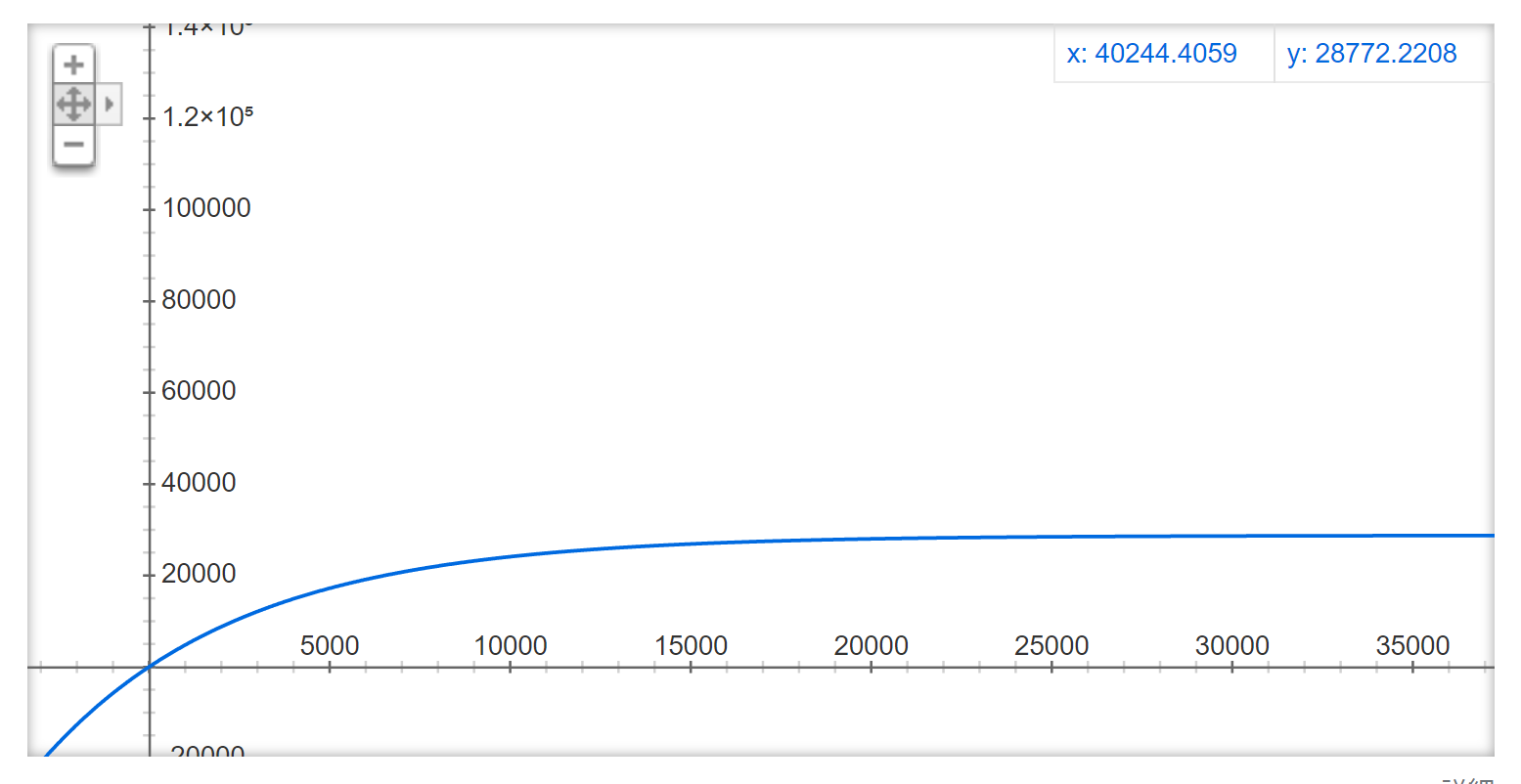
ここでt=3600(1時間)までのグラフを見ると、おおむねI(t)は線形のように見えます。
また、t=36000(10時間)までのグラフを見ると、飽和しているグラフだということが分かります。
I(t)のt=∞の値を求めると
\lim_{t \to \infty} I(t) = 28791.2
そうすると数式上は人間の短期記憶できる限界は28791.2[bit]です。したがって、これをByteに換算しなおすと、人間の短期記憶できる限界は3.6KBだと計算できます。
昔、人間の脳は短期記憶だと4GBぐらいのメモリしかない。というのをどこかで見たことがあるのですが、今調べても見つからないので私の記憶違いかも。
文章記憶の限界
法律で「常用漢字」というものが定義されています。これは、「法令、公用文書、新聞、雑誌、放送など、一般の社会生活において、現代の国語を書き表す場合の漢字使用の目安を示すもの」だそうです。したがって、日本語の文章は、この常用漢字の文字で表されると考えられます。この常用漢字が1945文字で、ひらがな・カタカナを合わせて100字なので、おおよそ2045文字。一般的な日本語の文章に含まれる文字は11bit程度で表現できると考えられます。
これらの条件とI(t)を元に、制限時間内で覚えられる日本語の文章を計算した表を作ります。
| 時間(分) | 情報量(Byte) | 日本語の文字数 |
|---|---|---|
| 5 | 191 | 139 |
| 10 | 372 | 271 |
| 15 | 544 | 395 |
| 30 | 1,005 | 731 |
| 60 | 1,730 | 1,258 |
| 90 | 2,252 | 1,638 |
| 120 | 2,628 | 1,911 |
人生の中で暗唱した長い文章はなんだろうか。ということを考えたのですが、中学時代に日本国憲法の前文を覚える。ということをやった記憶があって、今、調べて見ると650字程度でした。したがって、理論上は30分程度あれば覚えられる内容のようです。
また、Twitterが140字制限であることを考えると、完全に覚えるには5分程度で済むそうです。ツイートの内容を一字一句間違えずに覚えるのが5分以内。というのは、割と直感とズレないかな。と思いました。
私が学生の時代、授業の最初に「今日は何ページ進める」みたいなことを言っている先生がいました。それは、授業の回数とページ数を勘案して計画をしていたのですが、日によってはかなり無理のある授業をし、学生は理解できていなかった。といったことがありました。それは記憶の物理限界を超えているのでは?と思うことがありました。今回の試算で、60分の講義で進められる文字数というのは、1,200文字程度しかないのではないか。と感じました。もちろん。これは目安です。60分で完全記憶できる文字数が1,200文字であって、その知識は何Byteであるかは議論していません。他にもボトルネックは存在して、教師が教科書を読んで説明するのであれば、60分間で発話する限界の文字数もあります。
感想
中学ぐらいのときに「5次方程式の解の公式は存在しない」ということを、何かの本で知りました。
その後、色々ネットで調べたり、本を買ったりして読んだこともあるのですが、自分では"理解した"と言えるレベルには達していません。
一方で、歴史的に見ると「5次方程式の解の公式は存在しない」という証明は1824年に完成しているようです。
そこで、私は思うことがありました。
「なぜ自分は200年前の数学の証明が分からないのであろうか」
問いは、自分への不満ということもありますが、200年前の人が出来たことが現代の自分では出来ない。というのは、なぜでしょうか。
200年前に比べ、科学は多く発展し、資料も豊富にあるにも関わらず、その証明が分からないのは、なぜでしょうか。
そして、
「200年前の数学を分からなくて良いのだろうか」
という疑問もあります。
大学時代の講義や内容を手足のごとく使いこなせている人はどれだけいるのでしょうか。
実際問題として、ガロア理論が出来なくても社会生活上困ることは、私は、ほぼ無いです。
「理解している」ということも妄想であるかもしれません。
そのような抽象的な問いに対し、1つ思ったことは、「人間の覚えられる限界」があるのではないか。という仮説でした。
確かに、教育のカリキュラムにおいて、「専門教育を〇〇時間以上学んだ者」という表記があったり、第一種電気工事士を受けるためには実務経験は3年必要だったりします。
したがって、「人間の理解の速度には限界があり、知識の蓄積の証明の担保には時間でしか証明できない」ということなのではないか。ということです。
では、「理解する」という以前に「人間の覚えられる限界速度と限界容量」を試算してみる。というのが今回の試みの1つでした。
しかし、これは本当に近似に過ぎません。先ほどのアーベル-ルフィニの定理のWikipediaのページの容量は23.3kBでした。これは本当に知識の容量を表しているのでしょうか?
前節の試算をもとにすると、2時間で2kB程度、人間は覚えられます。ということは、完全に覚えるには、1日2時間、12日勉強すれば理解できる想定です。これは当てになるのでしょうか?
おそらく「ないよりマシの試算」程度の試算です。
また「覚える」≠「理解する」ということではなく、「今日の天気は晴れです。」という文章を覚えても、「今日の天気は何ですか?」という問いには覚えただけでは答えられません。
脳内での知識の保持の仕方の変換が違いますし、推論もしなくてはなりません
たまたま昨日、ツイッターを見ていると面白いものを見つけました。
高級な知識そのものを売って暮らしたいというのは現代では無理筋よね。
— Kohta Ishikawa (@_kohta) March 20, 2022
「高級な知識」の種類が増えすぎてどれがいつ使えるのか全く分からないので、ボトルネックは知識そのものではなく今使えるのはどれなのかを探す方であって、その先にも具体的に適用するための微調整やスケールさせる方法とか色々な壁が列を成している。
— Kohta Ishikawa (@_kohta) March 20, 2022
習得もボトルネックなので、ノートだけ渡されてもそれを(素早く)脳に染み込ませるところまで面倒見ないと、知識そのものを目的としてやっている人達以外は、やってられないからその知識を使わずにどうにかする方法を考えようという方向に行ってしまう。
— Kohta Ishikawa (@_kohta) March 20, 2022
最近の流れ。とも思いますが、プログラミングを勉強するのにコンピューターサイエンスは要らない。という風潮を感じます。それ自身は、(私は)あまりよくないとは思いますが、一方で、Wordpressの導入や、Webアプリを書くのに、ビットや機械語レベルまで意識することはほとんどありません。
これはハードレベルを意識せずにプログラムを組めるようになり、プログラムの門戸が開かれた。という面もあります。私は、かなりプログラムの設計にこだわりがありますが、プログラムの設計も知識が高度化されすぎたのだろう。ということを思い始めました。社会が劇的な変化をするため、プロトタイプを作って、ビジネス検証をし、それを廃棄する。というサイクルを高速で回す必要が生まれています。そのため、長期でプロダクトを生かすための設計スキルというのは、相対的に価値が下がり、プロトタイプ力の方が珍重されています。これは社会の問題もあり、「高度な知識」のような「マネタイズまでのレイテンシの大きな知識」は、勉強しても、「金を稼げるくらい練度が上がったときには稼ぎ時をつかみそこねる」ため、「リスクが高い」という状態になっています。
「本質的に学習困難な知識はどのように理解すべきか」
「現代において学習困難な知識でどうやって稼ぐか」
究極、「学習困難な知識は理解しなくて良い」「人が求める=稼げる技術を勉強する方が良い」というのは一面的には正しいのかもしれません。