単純選択ソート
前回の記事ではソートの勉めを始め、ベーシックなバブルソートについても触れましたが、
今回はそこから派生する単純選択ソート、単純挿入ソートについて見ていきたいと思います。
まずは単純選択ソートですが、ざっくりいうと以下のようなものです
最小要素を先頭に移動し、2番目に小さい要素を先頭から2番目に移動するのを繰り返すアルゴリズム
だそうです。。小さい方の値をどんどん先頭寄りに持っていくことで昇順にするという感じみたいですね
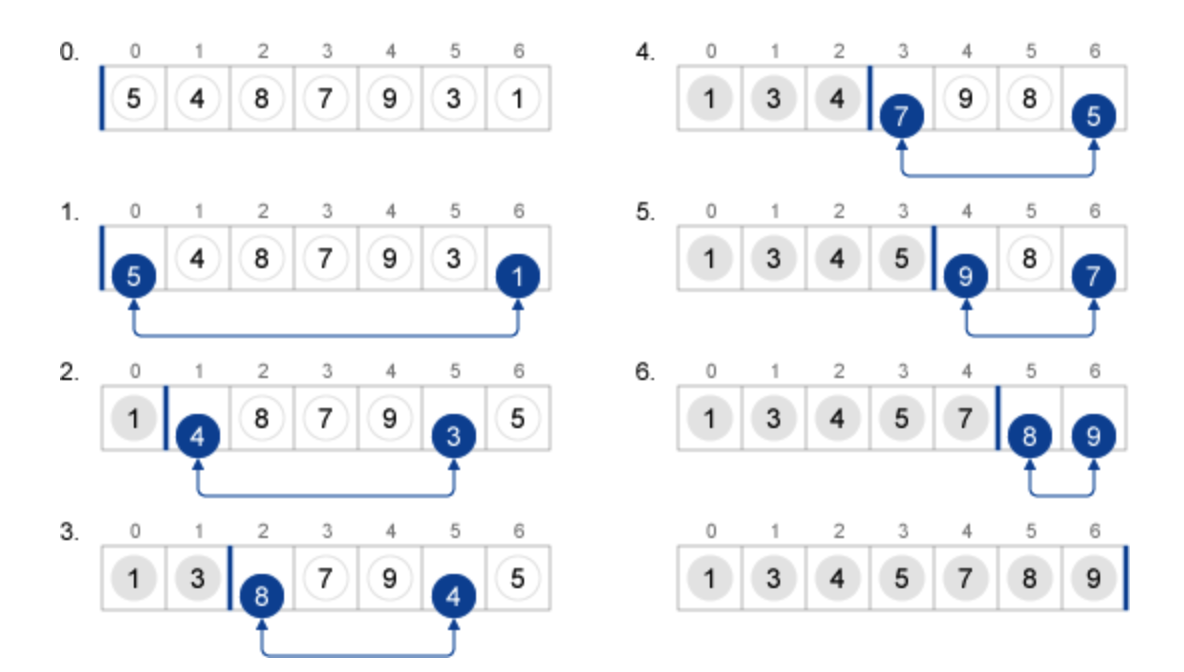
実際に{5,4,8,7,9,4,3,1} という順番がバラバラの数列で考えてみましょう!
まず着目するのは、最小の要素「1」 であり、配列の先頭に位置すべきなので、先頭要素の「5」と交換します。
すると、{1,4,8,7,9,3,5} という並びになるので、
次に2番目に小さい要素「3」に着目すると、
先頭から2番目の要素「4」よりも小さいので同様に交換を行います。
すると{1,3,8,7,9,4,5}という並びで2番目の要素までソートが完了しますね!
この過程を繰り返すと、下記のような流れになります。
常に小さい値を先頭寄りに交換することで、結果的に昇順になるという流れのようです。
言い換えれば、未ソート部(ソート対象としていない要素)から最小の要素を見つけ、
未ソート部の先頭要素と交換する操作を繰り返している
と言えます。
条件としてまとめると、、
① 未ソート部から最小のキーを持つ要素 a[最小値のインデックス]を選択する
② a[min]と未ソート部の先頭要素を交換する
隣、これを n - 1 回繰り返すと、未ソート部がなくなってソートが完了しそうですね。。!
一方で、この選択ソートアルゴリズムは、離れた要素を交換するため、安定ではありません。
同値が離れていた場合は、ソート後に前後が入れ替わってしまう可能性がありますね。。
例えば、{3,4,2,3,1}という配列をソートしようとして、
最初の3→1の交換で元々は先頭にあった「3」が末尾に入ってしまう、4番目の3よりも後ろになってしまう。。という
ことが選択ソードではあり得てしまうようです汗
諸々の条件を踏まえて、実際にコードに落としてみましょう!
public static void selectionSort(int[] a, int n) {
for (int i = 0; i < n - 1; i++) {
int min = i; // 未ソート部の最小要素のインデックス(最初は先頭要素のインデックスを格納)
for (int j = i + 1; j < n; j++) {
if (a[j] < a[min]) { // 最小値よりも小さければ、その値のインデックスをminに代入する
min = j;
}
}// 未ソート部の先頭要素と最小要素を交換する
swap(a, i, min);
}
}
上記はメソッドだけなので、ソートを行う配列の生成や、実際に交換を行うswapメソッドなどは
バブルソートの記事内に載せているのでそちらを参考にしてください!
先ほどの{5,4,8,7,9,3,1} を上のコードに当てはめて流れを追ってみましょう。
まずは 先頭インデックスである 0 が 最小値のインデックスとして min変数に代入され、
jはその右隣にあるインデックスから比較していく、という流れになります
j = 1から始まり、 j < 7 なので、そのままfor文の中に処理が移ります。
if(a[j] < a[min])は
a[1](4) < a[0](5) となるので、条件文は 4 < 5となり、
この時点の最小値は「4」 → min の値は「4」のインデックスである[1]となります
jがインクリメントされ、 2 < 7 なので、そのままfor文の中に処理が移ります。
a[2](8) < a[1](4) となるので、条件文は 8 < 4となり、「8」は最小値ではないので
そのまま次の繰り返しに移行します。
jがインクリメントされ、 3 < 7 なので、
a[3](7) < a[1](4) → 条件文は 7 < 4となり、「7」は最小値ではないので次の処理へ
jがインクリメントされ、 4 < 7 なので、
a[4](9) < a[1](4) → 条件文は 9 < 4となり、「9」は最小値ではないので次の処理へ
jがインクリメントされ、 5 < 7 なので、
a[5](3) < a[1](4) → 条件文は 3 < 4となり、この時点での最小値は「3」となるので
min の値は「3」のインデックスである[5]となります
jがインクリメントされ、 6 < 7 なので、
a[6](1) < a[5](3) → 条件文は 1 < 3となり、この時点での最小値は「1」となるので
min の値は「1」のインデックスである[6]となります j < 7なのでこのループは抜けて、
swap(a,0,6)が行われ、[0]である「5」と[6]である「1」が交換されるので
1ソート目を終えた時点で、{1,4,8,7,9,3,5}となります。
そのままiがデクリメントされ、1となるので、 minにも1が代入され、 j = 1 + 1 で2から始まります。
a[2](8)< a[1](4)→ 条件文は 8 < 4 となり、「8」は最小値ではないので次の処理へ
jがインクリメントされ、 3 < 7 なので、
a[3](7) < a[1](4) → 条件文は 7 < 4となり、「7」は最小値ではないので次の処理へ。。
という感じに繰り返していき、先頭寄の要素よりも小さい要素があれば最小値のインデックスを更新し、
末尾まで行った時点で、未ソート部の先頭要素と交換していくという流れになります。
やってることは最小値となる部分を選択して、先頭と交換を繰り返しているので、選択ソートと言われる感じでしょうか。。
単純挿入ソート
バブル、選択ときたので次に単純挿入ソートを見ていきましょう。
挿入と言われるくらいなので、値を要素の合間に入れ込んでいくイメージですが、
着目要素をそれより先頭側の適切な位置に”挿入する”という作業を繰り返してソートを行うアルゴリズム
という感じらしいです。。イメージは湧きますが、ちょっと分かりにくいのでこれも実際に流れを見て見ましょう
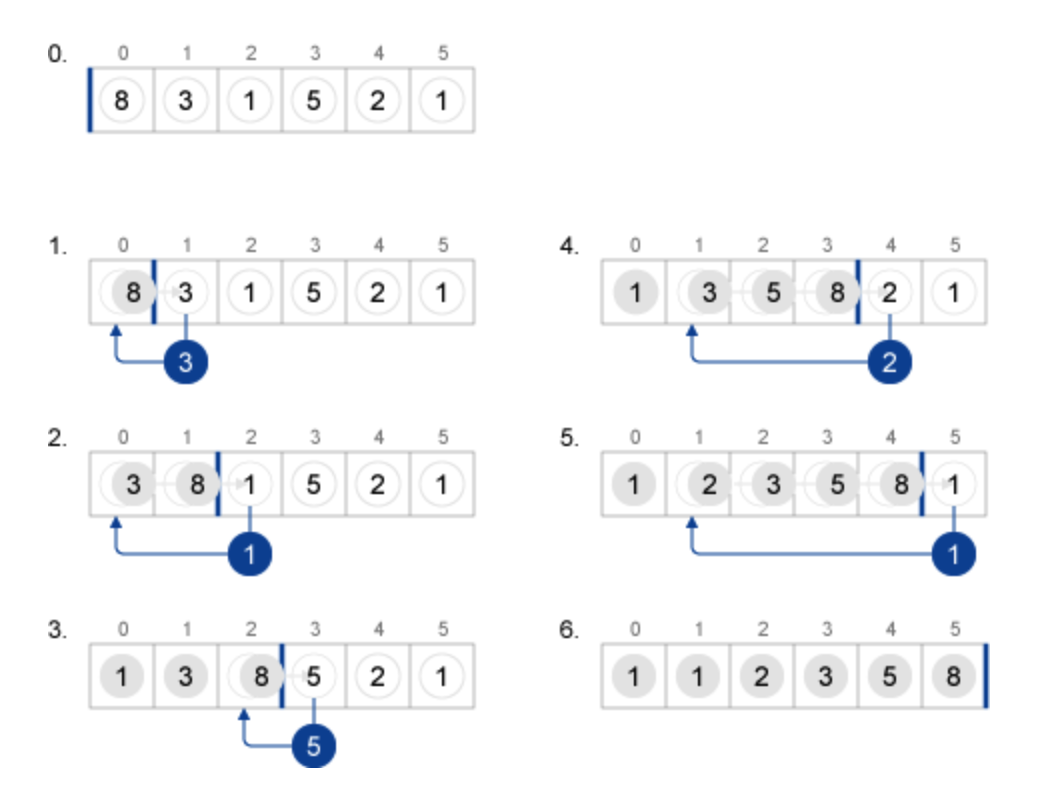
{8,3,1,5,2,1}という数列で考えてみます。
先頭の「8」をソート済として、2番目の要素の「3」に着目すると
「8」よりも小さいので、先頭寄りに位置すべきということになり、先頭に挿入すると、{3,8,1,5,2,1}となります
次に3番目の要素に着目し、「3」「8」と比べると、それよりも小さいので、先頭に挿入すると``{1,3,8,5,2,1}となります 次に4番目の要素の「5」に着目し、「8」よりも小さいので、8の手前に挿入すると{1,3,5,8,2,1}`となります。
というように、ソート済の要素と、未ソートの要素の先頭の値を比較して、大きい値があればその直前に挿入する
という操作を繰り返すことでソートを完了することができそうです。
ただ、この「直前に挿入する」という操作をコードで実現させるには少し工夫が必要そうです。
というのも、Javaには配列の要素を「適切な位置に挿入する」というメソッドがないんですね。。涙
配列で考えるならば、未ソート部において着目した要素よりも、その左隣の値が大きい限り
大きい方の値の右隣に、そのまま大きい方の値を代入し、
それ以下の要素に出会ったら、その位置に着目した要素を代入すルコとで実現できそうです。
と言葉にしてもピンとこないので、先ほどの続きをこの方法で操作してみましょう
{1,3,5,8,2,1}で終わっており、「3」→「1」→「5」と着目してきて、
それより手前の値に大きいものがあればその直前に挿入するというのを繰り返してきので、
次に着目すべきは5番目の要素である「2」ということになります。
その左隣は「8」で、「2」より大きいので比較した「8」の右隣にそのまま「8」を代入します → {1,3,4,5,8,8,1}
次も「5」の方が大きいので、「5」の右隣に「5」を代入して{1,3,4,5,5,8,1}となり
次も「4」の方が大きいので、「4」の右隣に「4」を代入して{1,3,4,4,5,8,1}となり
次も「3」の方が大きいので、「3」の右隣に「3」を代入して{1,3,3,4,5,8,1}となり
次の「1」ですが、ここで初めて「2」よりも小さい値に出会うので、
「1」の右隣に「2」を代入すると、最終的に{1,2,3,4,5,8,1}と、2を正しい位置に挿入することができます。
着目した要素を保存する一時変数を持たせて、左隣が大きいか小さいかで処理を分け、
小さければその右隣に一時変数を代入することで、結果的に「目的の位置に挿入する」という行為が実現できています。
(処理自体は比較と代入を繰り返しているだけなので、言い方がややこしいですが汗)
ここまでやり方が分かってきたので、実際にコードに落とし込んでみましょう!
static void insertionSort(int[] a, int n) {
for (int i = 1; i < n; i++) {
int j;
int tmp = a[i]; //一時変数
//走査する要素が先頭以外で、一時変数よりも値が大きい間は代入操作を続ける
for (j = i; j > 0 && a[j - 1] > tmp; j--) {
a[j] = a[j - 1]; //左隣に値を代入する
}
a[j] = tmp; //最小要素を先頭寄りに代入する
}
}
ソートの繰り返し制御用変数をjとして、着目する要素を一時変数として tmpに代入しています。
ソートを終了する条件は、下記条件のいずれかが成立したときとすれば良さそうです
- 目的列の左端に達した
- tmpと等しいか、それよりも小さい値を持った項目 a[j-1]が見つかった
2つのいずれか一方が成立するまでjをデクリメントして末尾から先頭への比較、代入操作を繰り返しています。
コード上では for (j = i; j > 0 && a[j - 1] > tmp; j--)となっていますが、言い換えると、
jが0より大きい(先頭以外のインデックス) かつ
a[j - 1]の値が一時変数よりも大きい
(もっと先頭寄りの方に代入する必要がある)間は代入操作を繰り返せばよいということになりそうです。
もし一時変数よりも小さければその時は繰り返し処理を抜けて、a[j] = tmpとして、
意図した位置への挿入(操作自体は代入)を行なっています。
仮に{1,3,5,8,2,1}という数列を最初からソートするとして、コードで流れを追ってみましょう。
■ i = 1から始まる
tmp変数には a[1]の3が代入される
もし j > 0 かつ、a[1-1] > 3 だったら代入操作を行うが、
この時点で既に a[0]の1の方が小さいので、代入操作は行わずにfor文を抜ける
a[1] = 3でそのまま変わらない → {1,3,5,8,2,1}
■ i =2 なので
tmp変数にはa[2]の5が代入される
もし j > 0 かつ a[2-1] > 5 だったら代入操作を行うが、
この時点で既にa[1]の3の方が小さいので、代入操作は行わずにfor文を抜ける
a[2] = 5でそのまま変わらない → {1,3,5,8,2,1}
■ i = 3 なので
tmpe変数にはa[3]の8が代入される
もし j > 0 かつ a[3-1] > 8 だったら代入操作を行うが、
この時点で既にa[2]の5の方が小さいので、代入操作は行わずにfor文を抜ける
a[3] = 8なので変わらない → {1,3,5,8,2,1}
■ i = 4 なので
tmp変数にはa[4]の2が代入される
もし j > 0 かつ a[4-1] > 2 だったら代入操作を行うが、
a[3] の8の方が大きいため、代入操作を行い、
a[4] に a[3]の8を代入 → {1,3,5,8,8,1}となる
もし j > 0 かつ a[3-1] > 2 だったら代入操作を行うので
a[2] の5の方が大きいため、代入操作を行い、
a[3] に a[2]の5を代入して {1,3,5,5,8,1}となる
もし j > 0 かつ a[2-1] > 2 だったら代入操作を行うので
a[1] の3の方が大きいため、代入操作を行い、
a[2] に a[1]の3を代入して {1,3,3,5,8,1}となる
もし j > 0 かつ a[1-1] > 2 だったら代入操作を行うが、
a[0] の1の方が小さいため、代入操作は行わず
a[1]にtmpの2が代入され、 {1,2,3,5,8,1}となり、2を前に出すことができました
これを繰り返すことで、昇順へのソートが完了しますが、
単純挿入ソートは、常に隣り合う値を比較、必要に応じて代入していくので、飛び越えた要素の交換は行われません。
そのため、安定したアルゴリズムとみなすことができます。
バブル・選択・挿入の比較
ここまでで学んできた3つのアルゴリズムを比較してみると下記のようになります。
| 種類 | 速度 | 安定性 |
|---|---|---|
| バブルソート | O(n2) | 安定 |
| 選択ソート | O(n2) | 不安定 |
| 挿入ソート | O(n2) | 安定 |
速度は変わらずで、選択ソートだけが離れた要素を交換する可能性があるので不安定という感じですね。。
あくまで考え方ですが、実装を少し変えるだけでもソートの動きが変わるのが実感できた気がします!
学んだこと
- 選択ソートは最小値インデックスを走査し、未ソート部の先頭と交換する
- 挿入ソートは着目要素を保存し、自分より小さい値を見つける位置まで代入を繰り返す(実質、挿入操作ではない)
バブル、選択、挿入と触れてきて、隣り合う要素の比較から、
最小値インデックスを使ったり、代入を繰り返したりと、ひとえにソートといっても
様々なやり方があることが分かりました。。!
とは言え、これらの速度はo(n2)というのは高速とは言い難く、、シェル、クイックソートというものがあるらしいので、
引き続き頑張っていきます!
※ 記事内の画像はAIZU online Judgeから拝借致しました。