ソートとは?
これまで線形探索や、ハッシュ法など、
データの集合から特定の値を見つける方法について学習してきましたが、
二分法など、要素が昇順にソートされていないと使えないものもありました。
単純なデータであれば問題ありませんが、実際に扱うデータ全てが昇順になっているということはまぁないと思います。
そこで出てくるのが、データをソートするということですが、ざっくりな定義だと以下のような感じになりそうです。
キーとなる項目の値の大小関係に基づいてデータの集合を一定の順序に並べ替える作業
ふむ、、このキーとなる項目は名前であったり、会員番号であったりと色々な種類のデータになりそうですが、
それらを大小関係を基に扱いやすく並び替える作業をソートと言うっぽいですね。
また、ソートには、安定なものとと不安定なものがあるらしく、
同一キーを持つ要素の順序がソート前後で維持されるのが安定しており、
安定でないアルゴリズムは元の順序だったりそうじゃなかったりと不安定になるみたいです。
例えば、以下のような人たちの成績を、点数が低い順に並べるとしたとき、
- 学籍番号1の人が80点
- 学籍番号2の人が50点
- 学籍番号3の人が50点
- 学籍番号4の人が70点
としたときに、2と3は同じ点数なので、入れ替わりは置きませんが、ソートの過程で入れ替わる可能性があれば
その方法は不安定なソートと言い表せるということですね汗
そんなこんなで、今回は安定なソートの代表格であるバブルソートについて学んでいこうと思います!
バブルソート
単純交換ソートとも呼ばれるようですが、その名の通り
隣り合う2つの要素の大小関係を調べて、必要に応じて交換を繰り返す、昇順にしたり、降順にしたりする方法のことです。
{5,3,2,4,1}と並んでいる数字の配列を昇順(小さい順のこと。数字が小さい方から昇っていくイメージ)
に並べ替えしたいとします。
左から、右へと数を上げていきたいので、末尾の値から大小を比較して、左の方が値が大きければ
入れ替える。。入れ替えた上で比較して、、という作業を繰り返していくのがバブルソートということですね!
4 1 を比較して 4 > 1 なので交換
2 1 を比較して 2 > 1 なので交換
3 1 を比較して 3 > 1 なので交換
5 1 を比較して 5 > 1 なので交換
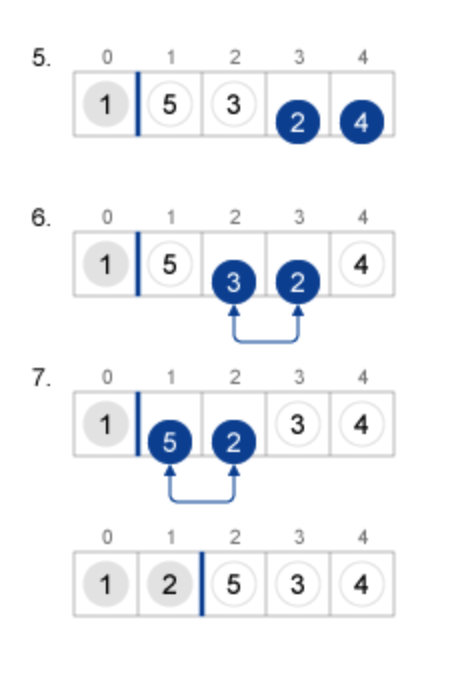
こうして1ソート目が終わった時点で{1,5,3,2,4,}となり、末尾にあった1を先頭に持ってくることができました!
続いて2ソート目にいくと、、
2 4 を比較して 2 < 4 なのでこのまま
3 2 を比較して 3 > 2 なので交換
5 2 を比較して 5 > 2 なので交換
こうして2ソート目が終わった時点で{1,2,5,3,4}となり、1の次に大きい2を2番目に持ってこれました。
これを繰り返していくと。。

4ソート目が終わった時点で、{1,2,3,4,5}と昇順に並べ替えることができました!
このソートを通じた比較、交換の作業をパスと呼ぶんですが、ここでソートとパスの回数をそれぞれ振り返ってみます。
4ソート目が終わった時点で、並び替えは完了しており
1ソート目:4回の比較(大小関係が異なれば交換)
2ソート目:3回の比較(大小関係が異なれば交換)
3ソート目:2回の比較(大小関係が異なれば交換)
4ソート目:1回の比較(大小関係が異なれば交換)
となると、要素数が5の配列のソートは4ソートで、パスする回数は1ずつ減るということになりそうです。
つまり。。
要素nの配列に対して n-1回のソートを行い、n-(ソートの回数)分のパスを行えば
最小要素を先頭に移動することができるということになりそうですね!
ここまでくればコードに落とし込めそうなので、実際に書いてみます!
import java.util.Scanner;
class BubbleSort {
//--- 配列の要素a[id1]とa[id2]の値を交換 ---//
static void swap(int[] a, int id1, int id2) {
int t = a[id1];
a[id1] = a[id2];
a[id2] = t;
}
//--- 単純交換ソート ---//
static void bubbleSort(int[] a, int n) {
for (int i = 0; i < n - 1; i++) {
for (int j = n - 1; j > i; j--) {
if (a[j - 1] < a[j]) {
swap(a, j - 1, j);
}
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("単純交換ソート(バブルソート)");
System.out.print("要素数:");
int nx = sc.nextInt();
int[] x = new int[nx];
for (int i = 0; i < nx; i++) {
System.out.print("x[" + i + "]:");
x[i] = sc.nextInt();
}
bubbleSort(x, nx); // 配列xをバブルソート
System.out.println("昇順にソートしました。");
for (int i = 0; i < nx; i++) {
System.out.println("x[" + i + "]=" + x[i]);
}
}
}
最初に入力された数字分の要素を持った配列を生成し、
次に入力される数字を格納後、配列の中の数字をバブルソートを用いて昇順にするという流れです。
実際にバブルソートを行っているのはbubbleSortメソッドということで中身を見てみると、
第一引数には、ソートしたい配列を、第二引数には配列の要素数を渡しています。
全体のソート回数はn - 1 回を行えばいいので、まずは外側のfor文を n - 1 回分だけ回しています。
各ソートごとに見ていく要素は末尾からなので、内側のループの初期化文はj = 要素数(n)-1であり、
更新文では、配列の先頭へとパスを行うので、jをデクリメントしている点も注意してください。
パスの回数はソートを繰り返すごとに減っていくので、更新文では j < iとして、
iはパスが済んでいる要素までのインデックスを表しているので、末尾(j)から、iの次の要素までを
パスの対象としています。
比較する際は、if (a[j - 1] < a[j])として先に来る要素の方が、後にくる要素よりも大きければ
昇順とは逆となるので交換が必要という判定になり、交換するswapメソッドを実行しています。
swapメソッドでは、ソート対象の配列と、交換したい先の値、後の値を引数に渡しており、
先に来る要素をまずは一時変数tに代入し、後にくる要素を先に来る要素の位置に代入しています。
その後、tの値を後ろに来る要素の位置に代入することで交換を行なっています。
このバブルソートは、
飛び越えた要素を一気に交換せず、常に隣り合う要素を比較し、必要に応じて交換するため、
同じ大きさであっても順序が変わるようなことはないので、安定したアルゴリズムということができますね!
改良してみる
先ほどのコードで昇順にソートさせることはできましたが、
{6,4,3,7,1,9,8}をソートさせるときのことを考えてみましょう。
7個の要素を持つので、7-1回のソートを 6,5,4,3,2,1回という回数でパスを行い、
必要であれば交換もするという流れになります。
1回目のソート:{1,6,4,3,7,8,9}パス回数は6回
2回目のソート:{1,3,6,4,7,8,9}パス回数は5回
3回目のソート:{1,3,4,6,7,8,9}パス回数は4回
4回目のソート:{1,3,4,6,7,8,9}パス回数は3回...
と続いていきますが、3回目のソートで既に昇順になっており、それ以降では要素は変わらないことが分かります。
ただ、ループ数は要素数に合わせて決め打ちをしているので、既にソートされている値もパスの対象になってしまい
無駄な処理が増えてしまっているようです。。
ともすれば、もし1度も交換が行われなければ、全ての値が昇順になっているという見方ができるので、
bubbleSortメソッドを修正してみましょう!
static void bubbleSort(int[] a, int n) {
for (int i = 0; i < n - 1; i++) {
System.out.println("ソート開始");
int exchg = 0; // パスにおける交換回数
for (int j = n - 1; j > i; j--) {
System.out.println("パスを行う");
if (a[j - 1] > a[j]) {
swap(a, j - 1, j);
exchg++;
}
}
if (exchg == 0) break; // 交換が行われなかったら終了
}
}
大小関係が逆であればswapを行なっていましが、その時点で、交換した回数を表すexhngカウントをインクリメントしています。
これが1以上カウントされていれば入れ替えが行われたので、それ以降もパスを通じた交換が行われる可能性がありますが、
これが0カウントであればパスが行われていない = ソート済となるので、if (exchg == 0) breakで打ち切っています。
パス回数によってソートの打ち切りをすることによって、
ソート済の配列や、それに近い状態の配列に対しては行う必要のない比較が大幅に省略されるので
短時間でソートが完了できそうですね!
もっと改良してみる
次に、{1,3,9,4,7,8,9}という7つの要素を持つデータに対してソートを行ってみますが、
1回目のソートで、6回のパスを通じて{1,3,4,9,6,7,8}というところまでソートが完了し、
2回目のソートで、5回のパスを通じて、、と続けたいところですが、
1回目のソートで既に 1,3,4という3つの要素のソートが完了していますが、
2回目のソートでも交換が発生するので、そのまま5回分パスを行なってしまいそうです。。
一連の比較・交換を行うパスにおいて、ある時点以降に交換がなければ、
それより先頭側はソート済となるということなので、
既にソート済の要素以外をパスの対象としてしまえばより効率は良さそうです。。
static void bubbleSort(int[] a, int n) {
int k = 0; // a[k]より前はソートずみ
while (k < n - 1) {
int last = n - 1; // 最後に交換した位置
for (int j = n - 1; j > k; j--) {
if (a[j - 1] > a[j]) {
swap(a, j - 1, j);
last = j;
}
k = last;
}
}
}
各ソートで最後に交換した2要素のインデックスを格納するためのlast変数を定義しました。
(初期値は、配列の要素の最後になるので、n-1で末尾インデックスを格納しています)
swapメソッドを通じて
交換を行うたびに値が大きい方の要素のインデックスの値をlastに代入しています。
1巡のソートが終了した時点で、lastの値をkに代入することによって、
次に行われるソートの範囲がa[最後に交換が行われた要素]までに限定することができます。
もし要素が交換されれば、交換される際に大きかった方の値のインデックスがjに入るので
{1,3,9,4,7,8,6} であれば
1ソート目の最後に交換された 9,4 の内、大きい方である9のインデックスである3が入り、
ソート後は{1,3,4,9,7,8,6}となるため、次のソートでパスする対象は末尾インデックス~4(値的には7)までということになります
if (a[j - 1] > a[j])にて、a[3]= 9 > a[4]= 7となるため、9,7の交換が最後に必要なパスとみなすことができそうです。
要素数と連動するソート回数とパス回数を決め打ちでやるところから
そもそもパスを通じた交換が1度も行われなければソート済と判断し、
最後に交換が行われた値のインデックスを用いて探索範囲を限定するところまで改善させることができました!
学んだこと
- ソートには安定したソートと、同値で順序が変わってしまう可能性のある不安定なソートがある。
- バブルソートでは、対象となるデータの要素数によってソートする回数とパスの回数を決められる。
- 交換する回数、インデックスを用いて無駄な処理を削ることができる。
基本ループから、探索へと進んでいったアルゴリズム修行ですが、
いよいよソートへと突入していき、よりアルゴリズム感が強くなってきた気がします。。(あくまで個人の見解です)
とは言え、考え方は配列だったりのデータの集合をJavaという枠組みでどう扱っていくかに尽きると思うので
まずは考え方の理解、コードへの落とし込み、効率の良い改善という流れで引き続き頑張っていこうと思います!
※記事内の画像は下記サイトより拝借致しました。
AIZU Online Judge