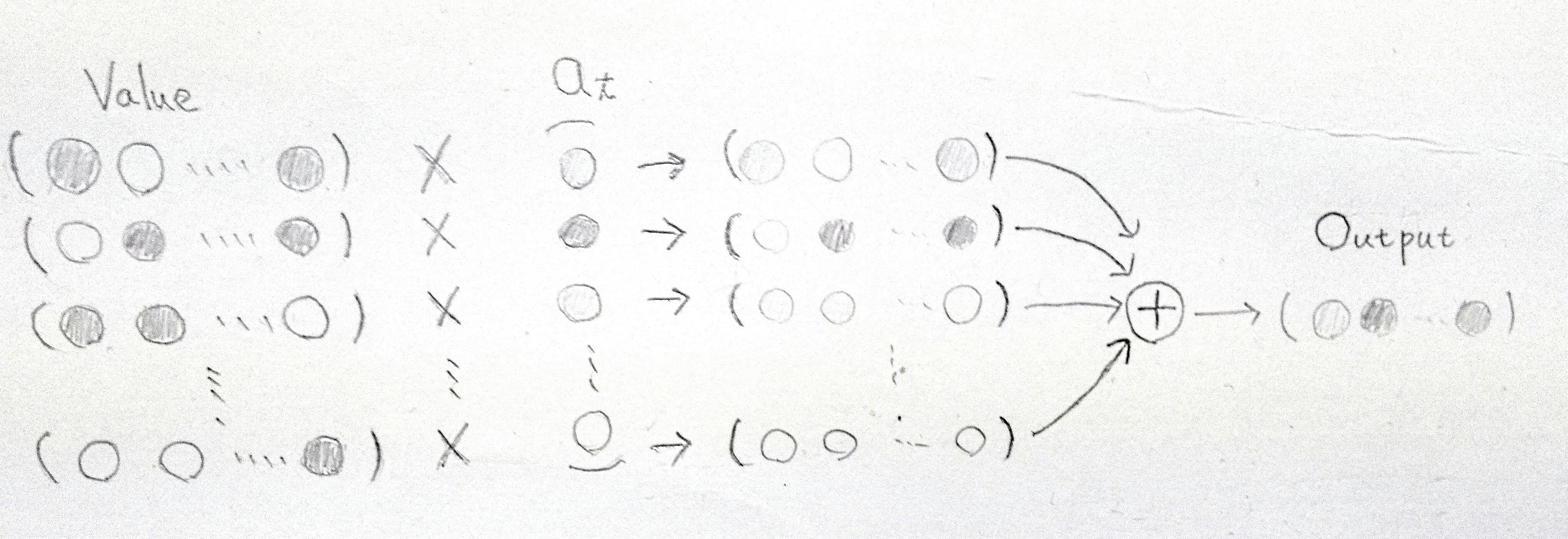Attentionの勉強

自分用のメモかつ記事を書く練習
間違ってても責任は取りません

Attentionの概要

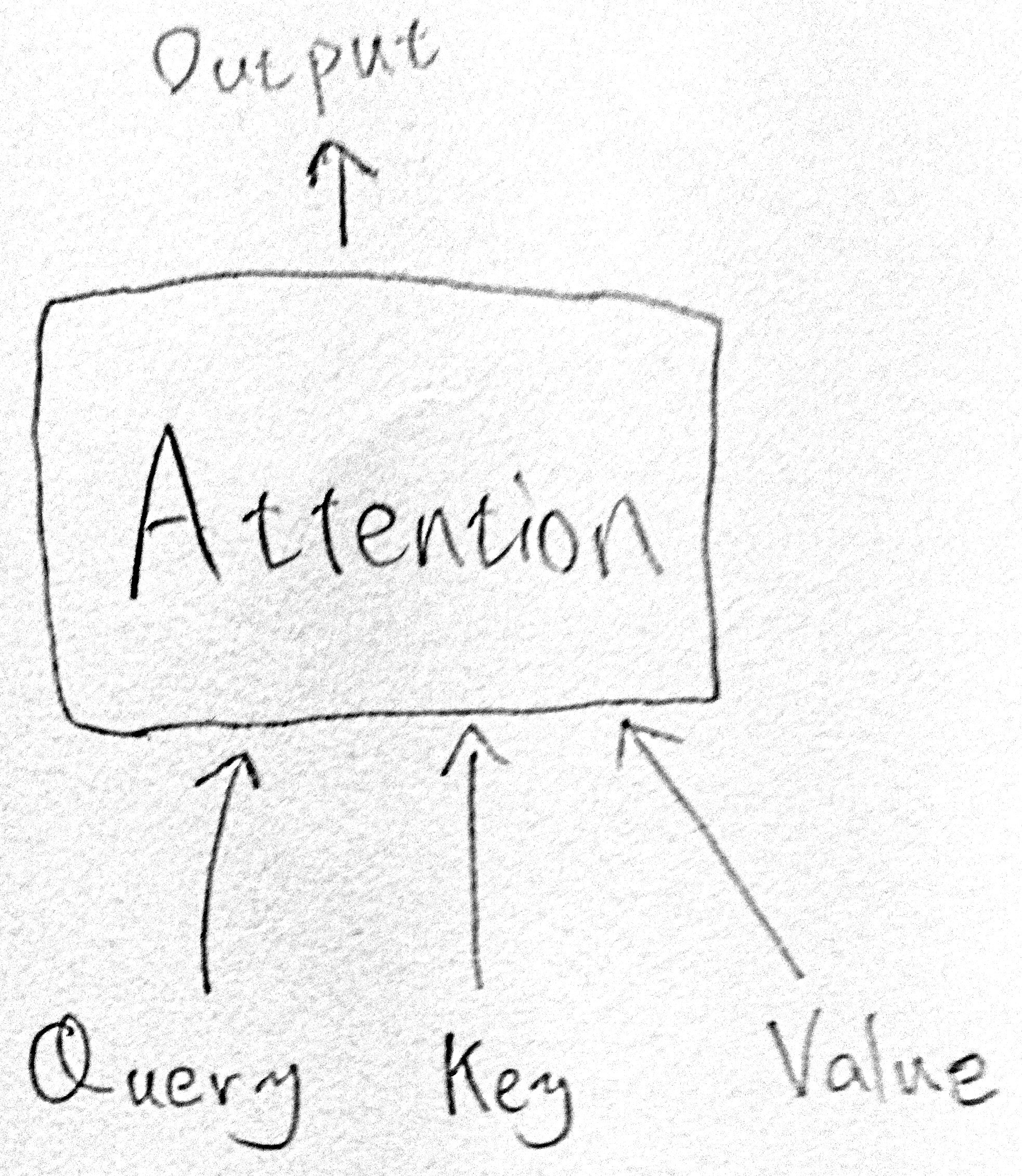
Attentionの入力はQuery,Key,Valueの3つ．
ここではKey,Valueは行列，Queryはベクトルとして説明する．
(Queryが行列になってもQueryの各行に対して同じ計算をするだけ?)

Attentionの出力はValueらをアライメントベクトル$a_t$で加重平均をとることで求める．

$a_t$の各要素はそれぞれのKeyとQueryがどれだけ似ているかを表すため，AttentionはQueryと等しい（似ている）Keyに対応するValue（に近い値）を出力する．

そのため，Attentionは辞書のような役割を果たす．

d = { Key1 : Value1 , Key2 : Value2 ,... }
d[Query]

$a_t$の要素は各KeyとQueryを入力とするscore関数で求められる．
（但し，$a_t$の総和を1にしたいため$Softmax$を取る）

   a_{t}^{(i)} =Softmax\left(score\left(Key_{(i)},Query\right)\right)

KeyとQueryの近似度を求めるために内積を使う．
他のscore関数と比べ，速度・メモリ使用量に優れる．また，学習するパラメータがない．

score\left(Key^{(i)},Query\right)=Key_{(i)}^TQuery

Transformerは内積を使用している．TransfomerのAttention全体は以下の式で表される．

Attention(Query,Key,Value)=a_tV=Softmax\left(\frac{Key^TQuery}{ \sqrt{d_k}}\right)Value

$d_k$はQuery,Key,Valueの次元．
$d_k$が大きい時に行の積が大きくなり勾配が小さくなってしまう(?)ため，スケーリングする．

学習可能パラメータとして行列$W_a$を入れたもの

score\left(Key^{(i)},Query\right)=Key_{(i)}^TW_a Query

score\left(Key^{(i)},Query\right)=v_a^T tanh\left( W_a Concat\left(Key_{(i)}^T,Query\right) \right)

時系列のAttentionには，Key,Valueに入力する範囲によってGlobalとLocalに分けられる．
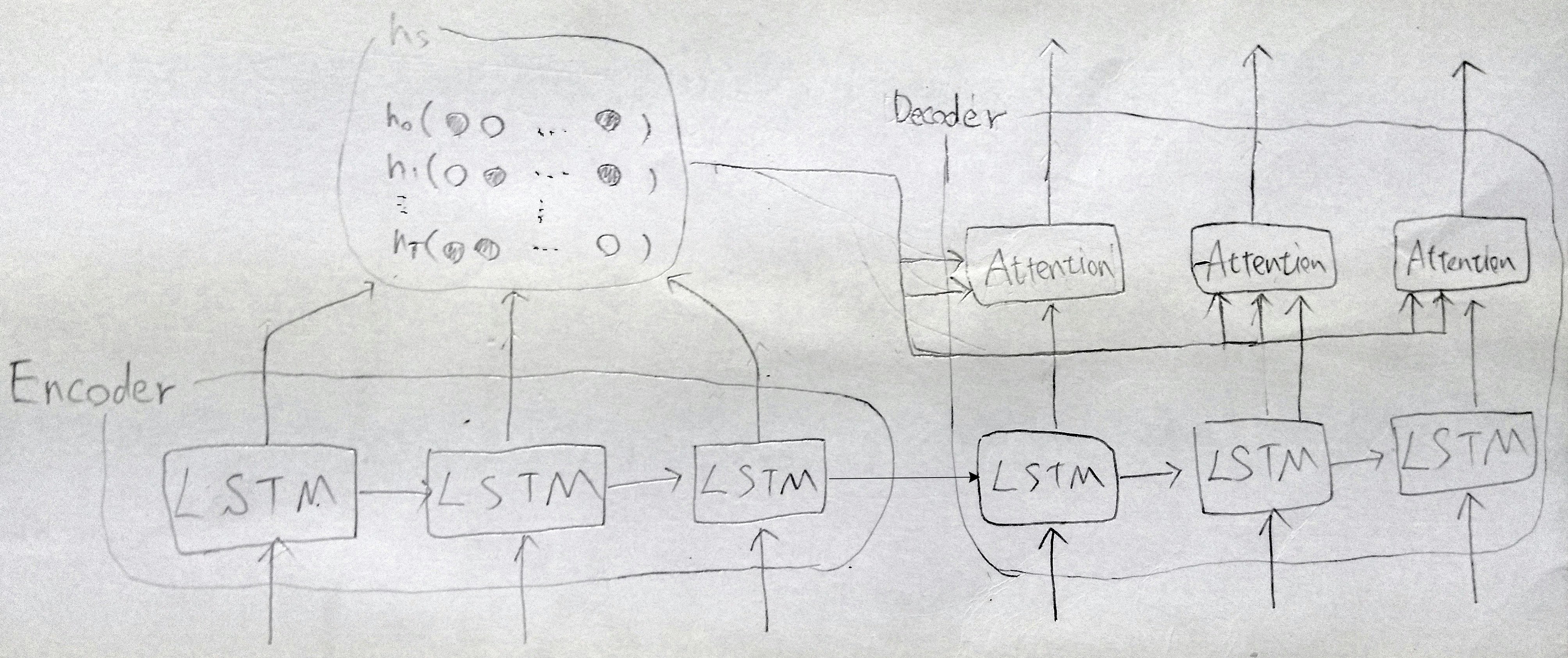
ここからは以下のSeq2Seqで考える．

AttentionにはKey,ValueとしてEncoderの隠れ状態hs，QueryとしてDecoderのLSTMセルの出力hが入力される．

AttentionのKey,ValueにEncoderが出力する隠れ状態をすべて入力する．
普通のAttention

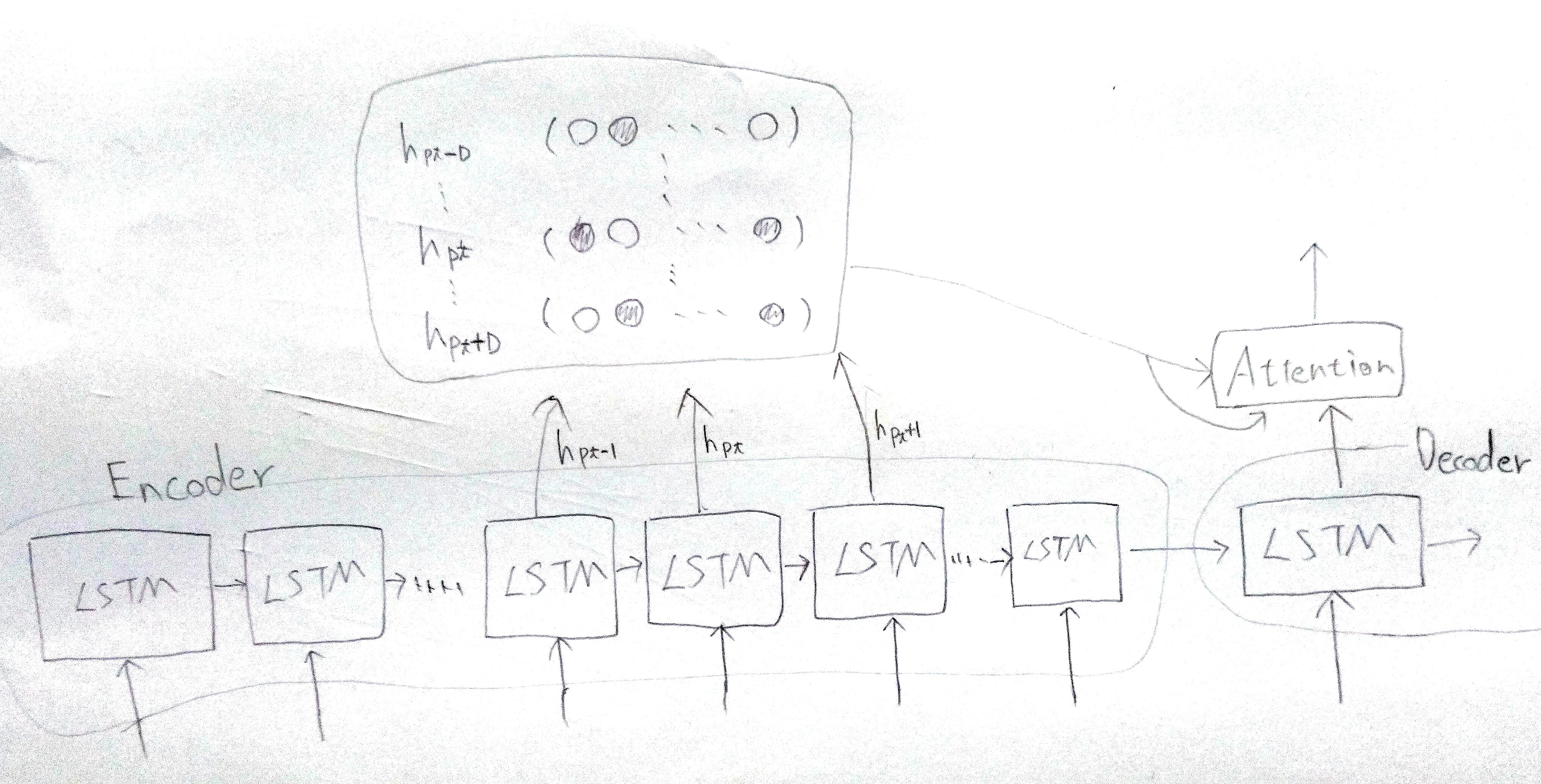
隠れ状態のすべてでなく一部を，AttentionのKey,Valueとして入力する．
すべての隠れ状態をAttentionに入力するのは，段落や文書など長いシーケンスの場合には向かないため，Local Attentionでは一部の隠れ状態のみをAttentionに入力する．

$h_{p_t-D}$から$h_{p_t+D}$までの隠れ状態をKey,Valueとして入力する．
定数Dは経験的に決めておく．

Local Attentionは$p_t$の決め方等によって種類がある．

$p_t=t$とする方法．
出力シーケンスのt番目の要素は，単純に入力シーケンスのt番目の要素の周辺と対応していると仮定する方法．
アライメントベクトル$a_t$は先ほどの式で求める

その都度，適切な$p_t$を求める方法．
この方法では$p_t$は実数として求める．
$p_t$は以下の式で求める．

$v_p$,$W_p$は学習可能なパラメータ．
$h$はAttentionのQueryとして入力されるDecoder側の隠れ状態．
$T$はEncoderに入力されるシーケンスの長さ．

p_t=S \times sigmoid\left(v_p^Ttanh\left(W_ph\right)\right)

また，アライメントベクトル$a_t$は以下の式で求める．
正規分布$N(p_t,\sigma^2)$を重みとしてかけていて，$p_t$により近い位置の単語に注意が向きやすくする．
$\sigma$は経験的に$\sigma=D/2$がいいらしい．

   a_{t}^{(i)} =Softmax\left(score\left(Key_{(i)},Query\right)\right)\times exp\left(-\frac{\left(i-p_t\right)^2}{2\sigma^2}\right)