畳み込みニューラルネットワークすごさを従来の機械学習のアルゴリズムと比較する

畳み込みニューラルネットワーク（CNN）が画像判別でよく使われるというのは知っていても、従来の機械学習アルゴリズムと比較してどれぐらいすごいものなのかというのがいまいちピンとこなかったので確認してみました。だいぶ長いよ！

概要

機械学習のアルゴリズムとして、ディープラーニングが出る前は例えばロジスティック回帰、サポートベクトルマシン、ランダムフォレストなどがありました。従来の手法というと漠然としますが、Scikit-learnでできるアルゴリズムと考えてよいです。これらの手法は現在でも有効で、これらのどれを使っても、手書き数字（MNIST）に対して最低でも8割、ちゃんと実装すれば9割の精度は出ます。Scikit-learnはとても使いやすいライブラリで、学習効率・実装効率ともによく、計算が比較的簡単なので高速です。逆にその段階で9割近く出ちゃうと、「学習が大変で処理も遅いディープラーニングって正直やる意味あるの？」って思ったのが疑問の発端です。

この記事では、MNISTより分類が難しいデータセットとしてCIFAR-10を用いて、従来の手法とディープラーニングで用いられる畳み込みニューラルネットワークの精度を比較します。最先端の畳み込みニューラルネットワークよりはだいぶチープなモデルですが、ディープラーニング登場前の手法より速く、効率的かつ高い精度をもって分類できることが確認できました。それを見ていきます。

CIFAR-10の可視化

CIFAR-10はKeras.datasetから読み込むことができます。Kerasは後のCNNの実装でも使えますが、Numpy配列としてScikit-learnに渡すことが可能です。前半はこの方法を中心に見ていきます。

まずはデータを可視化します。このデータは32×32×3のカラー画像で、10個のクラスから構成されています。飛行機、自動車、鳥、猫、鹿、犬、カエル、ウマ、船、トラックの10個のクラスからなります。まずはそれを見てみます。

import numpy as np
import matplotlib.pyplot as plt
from keras.datasets import cifar10

# データの読み込み
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
# 小数化
x_train = x_train / 255
x_test = x_test / 255
# ViewData
fig = plt.figure(figsize = (8, 8))
fig.subplots_adjust(hspace=0, wspace=0)
for i in range(10):
    index, cnt = 0, 0
    while(True):
        if y_train[index] == i:
            ax = fig.add_subplot(10, 10, i*10+cnt+1, xticks=[], yticks=[])
            ax.imshow(x_train[index])
            cnt += 1
        if cnt >= 10: break
        index += 1
plt.show()

コード：https://gist.github.com/koshian2/31042a7a258ba67ad3b0776ab4513908

訓練データは5万件、テストデータは1万件です（事前に分けられています）。データはSklearnのload_digits()と同様に、Keras.datasets.cifar10.load_data()から読み込むことができます。imshowでちゃんと表示できるように[0,255]のピクセル値を255で割って、[0,1]にマッピングします。

例えば3行目の鳥を見ると、顔だけアップになって背景画像に溶け込んでいるもの（5列目）から、全身がドアップになっているもの（3列目）までかなりバリエーションがあります。4行目の猫なんかは背景画像が白から赤までいろいろあります。カラー画像版のMNISTということでよく論文で出てきますが、問題設定としては黒字に白文字の手書き数字のMNISTよりもはるかに難しいデータセットです。

このCIFAR-10を従来の手法として、ロジスティック回帰、サポートベクトルマシン、ランダムフォレストの3種類で分類してみます。

##従来の手法でのカラー画像の分類
実はカラー画像の分類というのは、ディープラーニングを使わなくても従来の機械学習の手法でできます。MNISTと同じように画像をベクトルにしてしまえばいいのです。減色操作をしてもいいですが、しなくてもできます（しかも減色操作をしないほうがうまくいきます）。

例えばMNISTの場合、28×28×1（白黒なので1チャンネル）を784次元のベクトルとしました。CIFAR-10の場合は32×32×3（RGBなので3チャンネル）を3072次元のベクトルとします。つまりベクトルを見ると、

[(0, 0)の赤], [(0, 1)の赤], ……, [(31, 31)の赤], [(0, 0)の緑], ……, [(31, 31)の緑], ……, [(31, 31)の青]

という並びになります。「こんなベクトルで検出できるの？同じ座標の赤と緑の位置めちゃくちゃ離れてるじゃん」って最初不思議だったのですが、できます。MNISTでできたのだからできます。

###1.ロジスティック回帰
まずはおなじみのロジスティック回帰。データの読み込み以外はすべてSklearnでできます。

import numpy as np
import matplotlib.pyplot as plt
from keras.datasets import cifar10
from sklearn.linear_model import LogisticRegression
import time

start_time = time.time()
# データの読み込み
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
# 小数化
x_train = x_train / 255
x_test = x_test / 255
# データ数
m_train, m_test = x_train.shape[0], x_test.shape[0]
# ベクトル化
x_train, x_test = x_train.reshape(m_train, -1), x_test.reshape(m_test, -1)
# ノルムで標準化
x_train = x_train / np.linalg.norm(x_train, ord=2, axis=1, keepdims=True)
x_test = x_test / np.linalg.norm(x_test, ord=2, axis=1, keepdims=True)

# ロジスティック回帰
logr = LogisticRegression()
logr.fit(x_train, y_train)
print("Elapsed[s] : ", time.time() - start_time)
print("Train :", logr.score(x_train, y_train))
print("Test :", logr.score(x_test, y_test))

コード：https://gist.github.com/koshian2/a5b8f904b371b7425b9cbaa54cdcad9d

前処理として、255で割るほか、同一データのノルムが全て1になるように標準化しています。これは後のサポートベクトルマシンの場合露骨に処理時間に差が出るので（SVMは特に変数の標準化が重要なアルゴリズムです）、そういうものだと思ってください。あとはいつものですね。

出力

Elapsed[s] :  329.31931829452515
Train : 0.41996
Test : 0.4072

訓練、テスト精度ともに精度が4割でした。ちなみにElapsed[s]は処理時間の秒数を表します。ロジスティック回帰の時点でMNISTが8,9割出していたのと比べると、だいぶスタート位置が低いです。それだけ分類が難しいということがわかります。その点では分類の難しさを見るのに、ロジスティック回帰のような簡単なアルゴリズムでどの程度精度が出るのかを一度確認しておくのは意味があると思います。**5分半で精度40%**というのをひとまず覚えておきましょう。

ちなみに処理時間は、Sklearnのデフォルト設定では並列処理を行わないので、CPUを1コアしか使っていません。後半のKerasを使った例では自動的に並列処理を行っているので、処理秒数のスケールが異なります。

###2.サポートベクトルマシン
カーネルなし（線形カーネル）のサポートベクトルマシン（SVM）で行った例です。ほとんどロジスティック回帰と同じで、ここだけ違うだけです。

from sklearn.svm import LinearSVC
svc = LinearSVC()

コード全文：
https://gist.github.com/koshian2/09c1c21dc08fbb769eaaf836c5d9940a

コード全文はgistにあげているので、必要ならそちらを見てください。

出力

Elapsed[s] :  275.0674293041229
Train : 0.45122
Test : 0.4062

結果は、5分弱で訓練精度45%、テスト精度40%なのでロジスティック回帰よりちょっといいぐらいです。SVMの場合標準化がとても重要で、ノルムで標準化している

# ノルムで標準化
x_train = x_train / np.linalg.norm(x_train, ord=2, axis=1, keepdims=True)
x_test = x_test / np.linalg.norm(x_test, ord=2, axis=1, keepdims=True)

この行をコメントアウトすると、

SVM標準化なし

Elapsed[s] :  3692.342868089676
Train : 0.4203
Test : 0.3093

なんと1時間以上かかってしまいます！しかも精度も落ちています。必ず標準化するようにしましょう。

###3.ランダムフォレスト
ランダムフォレストも非ディープラーニングながらも画像分類でかなり有効な手法で、サポートベクトルマシンよりも良い精度を出しているという報告が数多くあります（例えばこれ）。ランダムフォレストも同じくSklearnからでき、分類器を

from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier()

コード全文：https://gist.github.com/koshian2/ce491e1149203530ede91c5b5bad2365

こう変えただけです。ただし、デフォルトの設定はほぼ際限なく（決定木の葉に含まれるサンプルがmin_samples_split:デフォルト=2になるまで延々と）葉を作り続けるので、とても決定木が深くなります。つまりデフォルトの設定ではオーバーフィッティング（過学習）に注意する必要があります。実際デフォルトで実行すると、

出力

# デフォルト→Overfitting
Elapsed[s] :  30.51237440109253
Train : 0.99394
Test : 0.3576

「訓練精度99%！最強！？？」って思うかもしれませんがただのオーバーフィッティングです。決定木の深さ（max_depth）を制限することで正則化効果が得られます。max_depthをいくつか試したところmax_depth=8が一番良さそうでした¹。

rf = RandomForestClassifier(max_depth=8)

オーバーフィッティング対策

# max_depth=8
Elapsed[s] :  18.324826955795288
Train : 0.434
Test : 0.3717

オーバーフィッティングを解消しつつ、テスト精度も維持できています。しかしこれが18秒で出てくるってランダムフォレスト強いですね。

###4.カラー画像まとめ
ロジスティック回帰、サポートベクトルマシン、ランダムフォレストの結果をまとめます。

アルゴリズム	処理時間[秒]	訓練精度	テスト精度
ロジスティック回帰	329.3193183	0.41996	0.4072
サポートベクトルマシン	275.0674293	0.45122	0.4062
ランダムフォレスト	18.32482696	0.434	0.3717

どれもテスト精度40%前後で似たり寄ったりです。ランダムフォレストはmax_depth=8での結果です。ランダムフォレストは過学習の調整が必要そうなので、一番安定しているサポートベクトルマシンを従来の機械学習の手法の代表としてピックアップします。

次はこれをグレースケールに変換してどうなるのか確かめてみます。

##グレースケール＋SVM
###1.グレースケール化
グレースケールに変換してサポートベクトルマシンを使った場合はどうでしょうか？Wikipediaによると、RGB→グレースケールへの変換公式は次の通りです。

$$ Y = 0.2126R + 0.7152G + 0.0722B $$

グレースケール化の関数は次のようになります。

# グレースケール化
def to_grayscale(tensor):
    return 0.2126*tensor[:, :, :, 0] + 0.7152*tensor[:, :, :, 1] + 0.0722*tensor[:, :, :, 2]

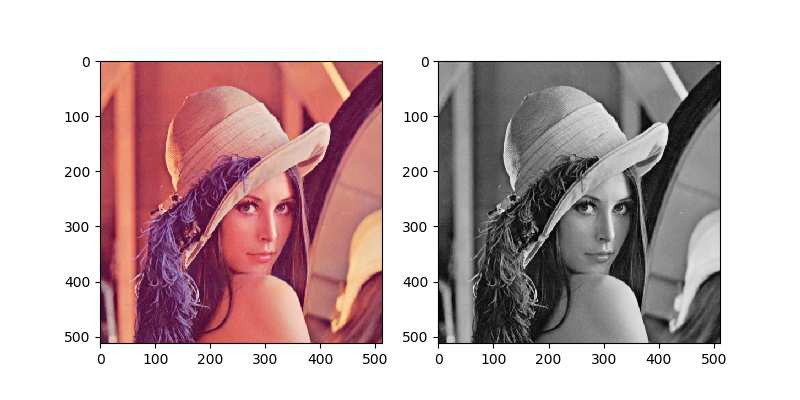
訓練データが(50000, 32, 32, 3)のテンソルだったので、(50000, 32, 32)のテンソルに変換しています。例えばおなじみのレナさんをグレースケール化するとこうなります。

import numpy as np
import matplotlib.pyplot as plt
from PIL import Image

# グレースケール化
def to_grayscale(tensor):
    return 0.2126*tensor[:, :, :, 0] + 0.7152*tensor[:, :, :, 1] + 0.0722*tensor[:, :, :, 2]

# 画像の読み込み
img = np.array(Image.open("lenna.png"))
img = img / 255
# 4階のテンソルにする
img = img[np.newaxis, :, :, :]
print(img.shape) #(1, 512, 512, 4)
# グレースケール
gray_img = to_grayscale(img)

# 表示
fig = plt.figure(figsize = (8, 8))
fig.subplots_adjust(hspace=0, wspace=0.2)
ax = fig.add_subplot(1, 2, 1)
ax.imshow(img[0])
ax = fig.add_subplot(1, 2, 2)
ax.imshow(gray_img[0], cmap="gray")
plt.show()

特に問題ありませんね（tif画像を32ビットpngとして保存したため4チャンネルになっていますが、今回は4チャンネル目は特に使いません）。

###2.SVMに適用
グレースケール化した画像をサポートベクトルマシンで読み込ませます。

import numpy as np
import matplotlib.pyplot as plt
from keras.datasets import cifar10
from sklearn.svm import LinearSVC
import time

start_time = time.time()
# データの読み込み
(x_train_origin, y_train), (x_test_origin, y_test) = cifar10.load_data()
# 小数化
x_train_origin = x_train_origin / 255
x_test_origin = x_test_origin / 255
# データ数
m_train, m_test = x_train_origin.shape[0], x_test_origin.shape[0]
# グレースケール化
def to_grayscale(tensor):
    # https://ja.wikipedia.org/wiki/%E3%82%B0%E3%83%AC%E3%83%BC%E3%82%B9%E3%82%B1%E3%83%BC%E3%83%AB#%E8%BC%9D%E5%BA%A6%E4%BF%9D%E5%AD%98%E5%A4%89%E6%8F%9B
    # Y = 0.2126R + 0.7152G + 0.0722B
    return 0.2126*tensor[:, :, :, 0] + 0.7152*tensor[:, :, :, 1] + 0.0722*tensor[:, :, :, 2]
x_train, x_test = to_grayscale(x_train_origin), to_grayscale(x_test_origin)
print(x_train.shape) #(50000, 32, 32)
# ベクトル化
x_train, x_test = x_train.reshape(m_train, -1), x_test.reshape(m_test, -1)
# ノルムで標準化
x_train = x_train / np.linalg.norm(x_train, ord=2, axis=1, keepdims=True)
x_test = x_test / np.linalg.norm(x_test, ord=2, axis=1, keepdims=True)

# サポートベクトルマシン
svc = LinearSVC()
svc.fit(x_train, y_train)
print("Elapsed[s] : ", time.time() - start_time)
print("Train :", svc.score(x_train, y_train))
print("Test :", svc.score(x_test, y_test))

コード：https://gist.github.com/koshian2/27f3bfdbe93287195daba65c6ed5de28

出力

Elapsed[s] :  91.28059148788452
Train : 0.3313
Test : 0.2901

案の定というか、やっぱりグレースケール化した分精度は落ちていますね。イメージとしては主成分分析をすると分散が減ってしまうため、高速化はするが精度は落ちるというのと同じような感じはします。主成分分析のほうがもっとちゃんと固有ベクトルを計算しているので、こんなふうにグレースケールの式をバンと与えてやるよりももう少し精度はよくなるはずです。しかし、カラー画像の精度を超えることはおそらくないでしょう。
CourseraのMachine Learningの授業でAndrew Ng先生が「プロジェクトの計画に、最初から主成分分析を使おうとする人がときどきいるが、なぜ最初から主成分分析を使わないでやろうとしないのか？」と疑問を呈していたことを思い出します。

##畳み込みとプーリング
###1.エッジ検出の理論
さて、畳み込みニューラルネットワークで使う重要なアイディアとして「エッジ検出」の概念があります。このエッジ検出は画像処理にもともとあった概念で、簡単な行列演算なのですが、ニューラルネットワークに組み込むととても強力に働く（CNN：畳み込みニューラルネットワーク）ことが知られれています。まずはそのエッジ検出をしてみます。

参考：http://www.mis.med.akita-u.ac.jp/~kata/image/sobelprew.html

ここではSobelフィルタを使います。Sobelフィルタとは、水平方向のエッジ検出フィルタを$F^H$, 垂直方向のフィルタを$F^V$として（べき乗ではない）、

\begin{align}
F^H = \left[\begin{array}{rrr}-1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{array}\right], F^V = \left[\begin{array}{rrr}-1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{array}\right]
\end{align}

これを元画像を3×3でスライスした領域と、要素積を計算して和をとる、つまり元画像の座標(i, j)の画素値が$I_{i,j}$であったときに、

\begin{align}
g_{i, j}^H=\sum_{k=0}^2\sum_{l=0}^2 I_{i+k, j+l}F_{k,l}^H \\
g_{i, j}^V=\sum_{k=0}^2\sum_{l=0}^2 I_{i+k, j+l}F_{k,l}^V
\end{align}

を計算します。出力画像Gは、

$$G = \sqrt{(g^H)^2 + (g^V)^2} $$

で計算します（表示する際はスケール調整をテキトーに入れるけど、CNNでは気にしなくてOK）。

例えば元の画像が、

\begin{align}
I = \left[\begin{array}{rrr}0 & 0 & 1 & 0 & 0 \\
0 & 1 & 1 & 1 & 0 \\
1 & 1 & 1 & 1 & 1 \\
0 & 1 & 1 & 1 & 0 \\
0 & 0 & 1 & 0 & 0
\end{array}\right]
\end{align}

という画像だったら、水平、垂直方向のフィルタを適用した結果は

\begin{align}
g^H = \left[\begin{array}{rrr}
3 & 0 & -3 \\
2 & 0 & -2 \\
3 & 0 & -3
\end{array}\right],g^V = \left[\begin{array}{rrr}
3 & 2 & 3 \\
0 & 0 & 0 \\
-3 & -2 & -3
\end{array}\right] 
\end{align}

となり、出力画像は、

\begin{align}
G = \left[\begin{array}{rrr}
4.24 & 2.00 & 4.24 \\
2.00 & 0 & 2.00 \\
4.24 & 2.00 & 4.24
\end{array}\right] 
\end{align}

です。小さすぎてよくわからないかもしれませんが、確かにエッジ検出できています。Pythonでの実装を見ていくともっと実感がつかめると思います。

###2.エッジ検出の実装
理論的なことはわかったので、実装を1からフルスクラッチで書いてみます。

import numpy as np
import matplotlib.pyplot as plt
from PIL import Image

def convolution_filter(img):
    # 縦方向のフィルター
    sobel_v = np.array([[-1,0,1], [-2,0,2], [-1,0,1]])
    # 横方向のフィルター
    sobel_h = np.array([[-1,-2,-1], [0,0,0], [1,2,1]])
    # カーネルサイズ
    kernel_size = 3
    # 出力画像
    out_img = np.zeros((img.shape[0]-kernel_size+1, img.shape[1]-kernel_size+1, 3))

    for i in range(kernel_size-1, img.shape[0]-kernel_size+1):
        for j in range(kernel_size-1, img.shape[1]-kernel_size+1):
            # スライス
            img_slice = img[(i-2):(i+1), (j-2):(j+1), 0:3]
            # 畳み込み
            conv_v = np.sum(img_slice * sobel_v, axis=(1,2))
            conv_h = np.sum(img_slice * sobel_h, axis=(1,2))
            # 代入
            out_img[i, j, :] = np.sqrt(conv_v**2 + conv_h**2)
    return out_img

# 画像を3回畳み込み
def conv_sample(img):
    titles = ["Original", "1st conv", "2nd conv", "3rd conv"]
    fig = plt.figure(figsize = (8, 8))
    fig.subplots_adjust(hspace=0.2, wspace=0.2)
    for i in range(4):
        ax = fig.add_subplot(2, 2, i+1)
        view_img = img / np.max(img) #表示用にスケール調整
        ax.imshow(view_img)
        ax.set_title(titles[i] + " " + str(view_img.shape))
        # 畳み込み
        if i!=3: img = convolution_filter(img)
    plt.show()

コード：https://gist.github.com/koshian2/30cdbefb878ee834b952803fc7501206

convolution_filterはエッジ検出フィルターです。入力画像にSobelフィルターを適用し、返します。convolution（畳み込み）と言っているのは、ここでやっていることCNNでの畳み込み層そのものだからです。CNNで置き換えると、カーネルサイズはフィルターの行列の要素数（この場合は3）、ストライドはこのフィルターを適用していくステップ（この場合は1）となります。わからなかったら特に気にしなくていいです。

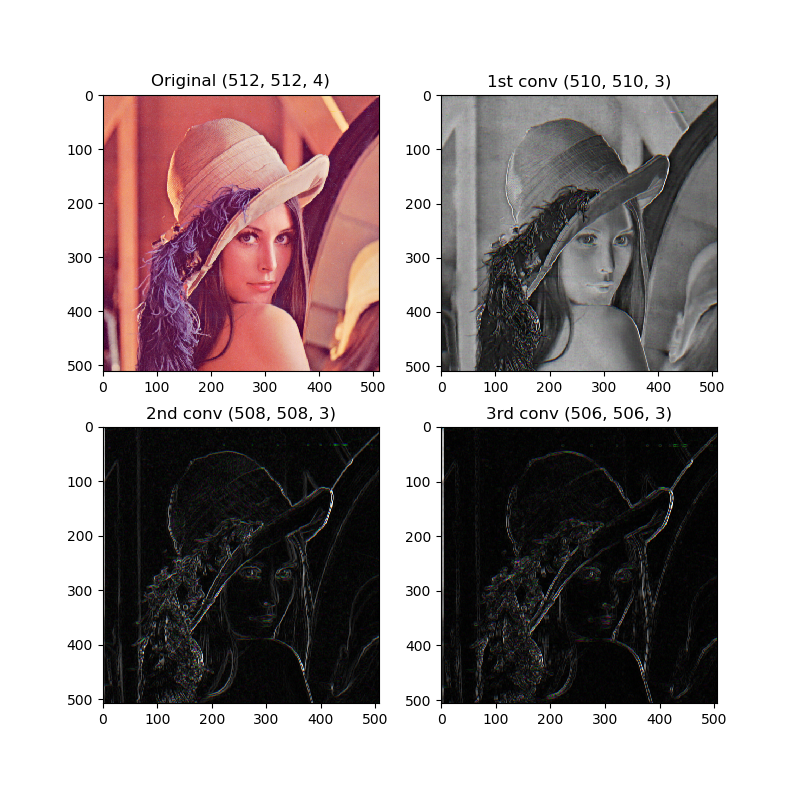
レナの画像を3回畳み込みしてみます。512×512の画像なので、1回目は510×510、2回目は508×508、3回目は506×506になります。

if __name__ == "__main__":
    # 画像の読み込み
    img = np.array(Image.open("lenna.png"))
    # 畳み込みサンプル
    conv_sample(img)

エッジ検出できていますね。

###3.エッジ検出＋SVM
ではエッジ検出した画像をSVMに食わせてみてはどうでしょうか？CNNで有効に働くのならSVMでも意味があるかもしれません。

start_time = time.time()
# データの読み込み
(x_train_origin, y_train), (x_test_origin, y_test) = cifar10.load_data()
# Infを出さないように255で割る
x_train_origin = x_train_origin / 255
x_test_origin = x_test_origin / 255
# データ数
m_train, m_test = x_train_origin.shape[0], x_test_origin.shape[0]
# 畳み込み変換用
x_train = np.zeros((m_train, x_train_origin.shape[1]-2, x_train_origin.shape[2]-2, 3))
x_test = np.zeros((m_test, x_test_origin.shape[1]-2, x_test_origin.shape[2]-2, 3))
# 畳み込み
for i in range(m_train):
    x_train[i, :, :, :] = convolution_filter(x_train_origin[i, :, :, :])
    x_train[i, :, :, :] = x_train[i, :, :, :] / np.max(x_train[i, :, :, :], axis=(0,1))
for i in range(m_test):
    x_test[i, :, :, :] = convolution_filter(x_test_origin[i, :, :, :])
    x_test[i, :, :, :] = x_test[i, :, :, :] / np.max(x_test[i, :, :, :], axis=(0,1))
# ベクトル化
x_train, x_test = x_train.reshape(m_train, -1), x_test.reshape(m_test, -1)
# ノルムで標準化
x_train = x_train / np.linalg.norm(x_train, ord=2, axis=1, keepdims=True)
x_test = x_test / np.linalg.norm(x_test, ord=2, axis=1, keepdims=True)

# サポートベクトルマシン
svc = LinearSVC()
svc.fit(x_train, y_train)
print("Elapsed[s] : ", time.time() - start_time)
print("Train :", svc.score(x_train, y_train))
print("Test :", svc.score(x_test, y_test))

コード全体：https://gist.github.com/koshian2/efd43655e307c181dac7f8e51202d98e

出力

Elapsed[s] :  1282.1308102607727
Train : 0.26964
Test : 0.2153

結果は、処理時間だけ増えて精度は下がってしまいました（元画像が5分で40%）。意味がないですね。エッジ検出自体に精度の向上があるわけではないようです。

###4.プーリング層の理論
CNNで畳み込み層と同じく使われるアイディアとしてプーリング、特にMaxプーリングがあります。これは簡単です。例えば、入力画像を2×2に分割し、

\begin{align}
I = \left[\begin{array}{rrr}
9 & 4 & -2 & 0 \\
7 & 2 & 3 & -5 \\
1 & 0 & -7 & 3\\
4 & 5 & -4 & 7
\end{array}\right] \to O = \left[\begin{array}{rrr}
9 & 3 \\
5 & 7 
\end{array}\right] 
\end{align}

というように出力することです。出力画像の(0,0)の9は元画像の上4つの最大値max(9, 4, 7, 2)=9、以下同様…というように計算します。これをCNNではカーネルサイズが2、ストライドが2の（MAX）プーリングといいます。切り出すサイズ（カーネル）が2、切り出すステップ（ストライド）が2なので。

プーリング層自体にエッジ検出のような効果はありませんが、画像を圧縮し、計算量を減らす効果があります。

###5. プーリングの実装
同じくレナの画像を畳み込み→プーリングしてみます。

# 画像をプーリング（パディング処理は未実装）
def pooling(img):
    #3x3でプーリング、strideも3
    kernel_size = 3
    out_img = np.zeros((int(img.shape[0]/kernel_size), int(img.shape[1]/kernel_size), 3))
    for i in range(out_img.shape[0]):
        for j in range(out_img.shape[1]):
            img_slice = img[(i*kernel_size):((i+1)*kernel_size), (j*kernel_size):((j+1)*kernel_size), :]
            out_img[i, j, :] = np.max(img_slice, axis=(1,2))
    return out_img

# 画像を3回畳み込み＋プーリング
def conv_pool_sample(img):
    titles = ["Original", "1st conv-pool", "2nd conv-pool", "3rd conv-pool"]
    fig = plt.figure(figsize = (8, 8))
    fig.subplots_adjust(hspace=0.2, wspace=0.2)
    for i in range(4):
        ax = fig.add_subplot(2, 2, i+1)
        view_img = img / np.max(img) #表示用にスケール調整
        ax.imshow(view_img)
        ax.set_title(titles[i] + " " + str(view_img.shape))
        # 畳み込み
        if i!=3: 
            img = convolution_filter(img)
            img = pooling(img)
    plt.show()

if __name__ == "__main__":
    # 画像の読み込み
    img = np.array(Image.open("lenna.png"))
    # 畳み込み＋プーリング
    conv_pool_sample(img)

コード：https://gist.github.com/koshian2/30cdbefb878ee834b952803fc7501206

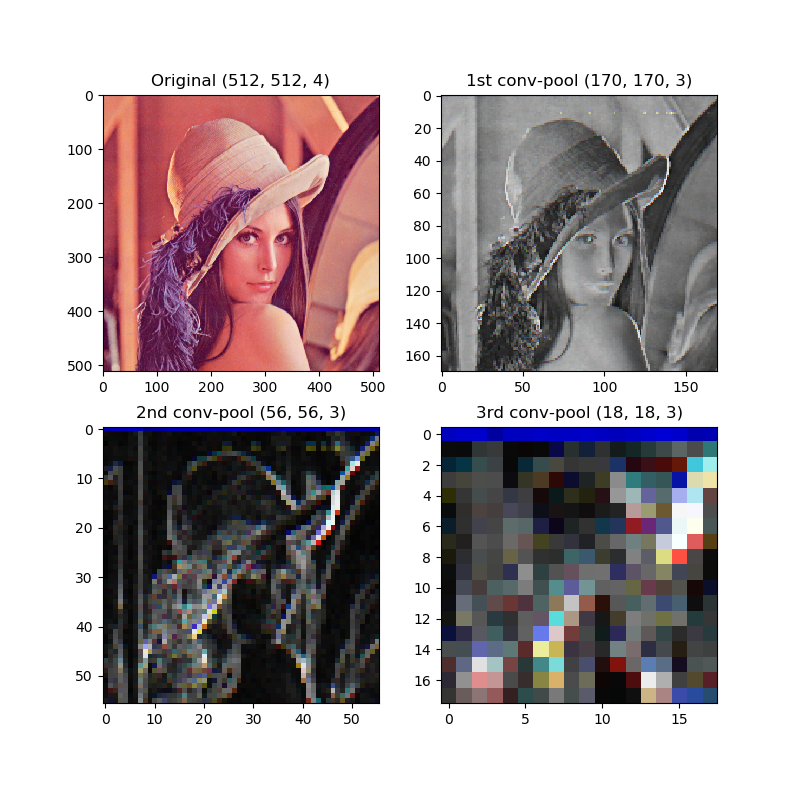
画素数だけ追っていきましょう。これのプーリングはカーネルサイズが3、ストライドも3なので、純粋に画素数が1/3になります。畳み込みはカーネルサイズが3、ストライドが1なので、画素数は-2になります。順に追っていくと、

1. 元画像512×512
2. 畳み込み510×510→プーリング170×170
3. 畳み込み168×168→プーリング56×56
4. 畳み込み54×54→プーリング18×18

はじめはエッジ検出だけだったのですが、3回目に独自の色が出ているのが面白いですね。

###6.畳み込み＋プーリング＋SVM
エッジ検出（畳み込み）＋SVMで見たように、CNNで用いられている畳み込み＋プーリングのアイディアを従来の機械学習に応用しても上手く動きません。前処理でこのような関数を定義し、

def preprocess(img):
    out_img = convolution_filter(img)
    out_img = pooling(out_img)
    out_img = convolution_filter(out_img)
    out_img = out_img / np.max(out_img, axis=(0,1))
    return out_img

このように変形してからSVMに食わせても、

# 畳み込み
for i in range(m_train):
    x_train[i, :, :, :] = preprocess(x_train_origin[i, :, :, :])
for i in range(m_test):
    x_test[i, :, :, :] = preprocess(x_test_origin[i, :, :, :])

コード全体：https://gist.github.com/koshian2/39ae085077818ad8a5afc5de56d44515

相変わらず処理時間だけ伸びて、精度は下がります。

出力

Elapsed[s] :  1036.8586645126343
Train : 0.22648
Test : 0.2222

###7.畳み込み＋プーリングのまとめ
畳み込み＋プーリングはエッジ検出と画像の圧縮を繰り返すアルゴリズムでした。ただし、これはニューラルネットワークで使うと上手く機能するアルゴリズムで、SVMのような従来の機械学習のアルゴリズムで使ってもほとんどメリットがありません。実際確かめてみると、

アルゴリズム	処理時間[秒]	訓練精度	テスト精度
SVM（カラー）	275.0674293	0.45122	0.4062
畳み込み＋SVM	1282.13081	0.26964	0.2153
畳み込み＋プーリング＋SVM	1036.858665	0.22648	0.2222

処理時間だけ伸びて精度は落ちるというやらないほうがいいパターンです。forループを使わなければもう少し処理時間は減ると思いますが、精度の低さは変わりません。つまり、エッジ検出自体に精度の向上は見込めず、グレースケール化したときのように元画像の分散が減れば精度も自動的に落ちる、という当たり前のことを確認していることでしかないのです。

ただし、繰り返しになりますがこのアイディアはニューラルネットワークで使うととても輝きます。それがとても不思議なのです。次は普通のニューラルネットワークで試してみます。

##ディープニューラルネットワーク
まずはごく普通の（全結合層だけの）ニューラルネットワークを作ってみます。これはSklearnでもできますが、ここからはKerasを使います。作るのは以下のモデルです。

• 入力層：3072ユニット（32×32×3）
• 第1層：768ユニット　ReLU
• 第2層：192ユニット　ReLU
• 第3層：10ユニット　Softmax　出力層

これをディープラーニングと言っていいのかどうかわかりませんが、使うユニットの数は膨大なのでディープではなくワイドなことは確かでしょう。

KerasはGPUを使えますがこのぐらいならCPUでも計算できますので、CPUで計算します。ただしKerasはデフォルトで並列化をするので、処理時間のスケールがデフォルトで並列化をしないSklearnとは異なります。自分が使っているCPUが4コアなのですが、SklearnではCPU使用率が25%までしか上がらなかったのに対して、Kerasの場合だと60%ぐらいまで上がります。なのでKerasのほうが2倍ぐらいの並列化効果は効いているはずです。

from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam
from keras.datasets import cifar10
from keras.utils.np_utils import to_categorical
import numpy as np
import time
import matplotlib.pyplot as plt

start_time = time.time()
# データの読み込み
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
# 小数化
x_train = x_train / 255.0
x_test = x_test / 255.0
# データ数
m_train, m_test = x_train.shape[0], x_test.shape[0]
# ベクトル化
x_train, x_test = x_train.reshape(m_train, -1), x_test.reshape(m_test, -1)
# ノルムで標準化
x_train = x_train / np.linalg.norm(x_train, ord=2, axis=1, keepdims=True)
x_test = x_test / np.linalg.norm(x_test, ord=2, axis=1, keepdims=True)
# yをOneHotVector化
y_train, y_test = to_categorical(y_train), to_categorical(y_test)

# モデル
print(x_train.shape) #(50000, 3072)
model = Sequential()
model.add(Dense(768, activation="relu", input_shape=x_train.shape[1:]))
model.add(Dense(192, activation="relu"))
model.add(Dense(10, activation="softmax"))

# コンパイル
model.compile(optimizer=Adam(), loss="categorical_crossentropy", metrics=["accuracy"])
# フィット
history = model.fit(x_train, y_train, batch_size=64, epochs=15).history
# 経過時間
print("Elapsed[s] : ", time.time() - start_time)
# テスト精度
test_eval = model.evaluate(x_test, y_test)
print("train accuracy :", history["acc"][-1])
print("test accuracy :", test_eval[1])
# 訓練誤差のプロット
plt.plot(range(len(history["loss"])), history["loss"], marker=".")
plt.show()

コード：https://gist.github.com/koshian2/c90cfe735331a6830cb3946425f9bc3b

Kerasはとてもわかりやすいインターフェイスをしています。コンパイル以下でmodel.summary()を実行するとモデルの詳細を表示してくれます。

_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
dense_1 (Dense)              (None, 768)               2360064
_________________________________________________________________
dense_2 (Dense)              (None, 192)               147648
_________________________________________________________________
dense_3 (Dense)              (None, 10)                1930
=================================================================
Total params: 2,509,642
Trainable params: 2,509,642
Non-trainable params: 0
_________________________________________________________________

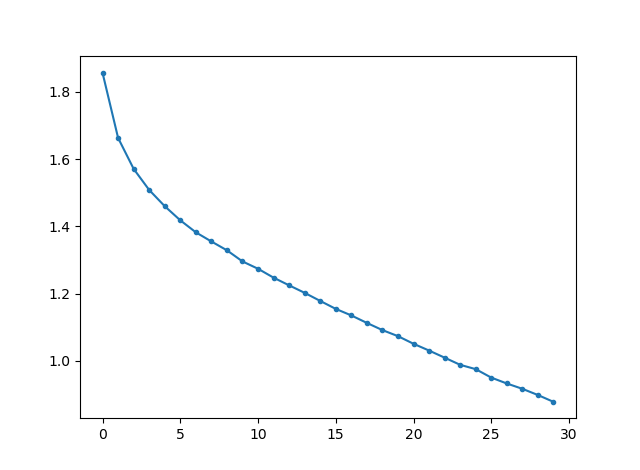
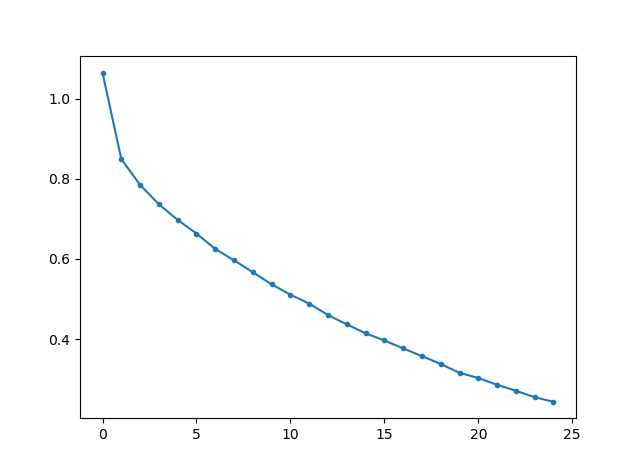
全結合層だけだとパラメーター多すぎ。epoch=15（15週）なら10分ちょい、epoch=30なら20分ちょいで終わります。epoch=30の場合の訓練データのコスト関数のプロットです。

まだまだコスト低下（訓練精度の向上）の余地はありますが、時間の関係で打ち切ってしまいました。訓練精度、テスト精度を比較します。

出力

# epoch=30の場合
Elapsed[s] :  1366.77405834198
10000/10000 [==============================] - 2s 167us/step
train accuracy : 0.68696
test accuracy : 0.5358

# epoch=15の場合
Elapsed[s] :  697.2960453033447
10000/10000 [==============================] - 2s 153us/step
train accuracy : 0.57604
test accuracy : 0.5231

ディープラーニングを使うことで、やっとSVMの4割の大台を突破することができました！ 要はCIFAR-10のような難しい問題だと、従来の機械学習アルゴリズムでは力不足だったということです。

ただし、この訓練精度、テスト精度を見ていると、epoch=15のときはさほど目立ちませんが、epoch=30の場合、両者の間に15%もの差がありオーバーフィッティング（過学習）しています。このまま学習を進めさせても、訓練精度の向上は見込めても、汎用的なテスト精度の向上はあまり見込めなさそうです。正則化やドロップアウトといった、High varianceに対する対策法が必要になります。

ちなみに、ニューラルネットワーク（これは畳み込みの有無に関わらずそうですが）を使うとちょっと嬉しいことがあります。それはメモリ使用量がSVMより少ないということです（もちろんそれはNNの規模によりますが、このぐらいだったらSVMより全然少ないです）。具体的な数値を出すと、SVMの計算中のメモリ使用量は4GB近かったです。ところが、このニューラルネットワークの学習中のメモリ使用量は（特にミニバッチ学習が効いている）、1.66GBでした。メモリ使用量が少なくて精度がいいというのが明らかになったので、やはりディープラーニングはする意味があるということが確認できました。

##畳み込みニューラルネットワーク（CNN）
いよいよ本題のCNNを実装します。今回は1から訓練させます。

1. 入力層：[32×32×3]
2. 畳み込み層：×10　kernel=3, stride=1 / [30x30x10]
3. 活性化層　ReLU
4. プーリング層　×10　kernel=3, stride=3 / [10x10x10]
5. 畳み込み層：×20　kernel=3, stride=1 / [8x8x20]
6. 活性化層　ReLU
7. バッチ標準化
8. 全結合層：1280ユニット
9. 出力層：10ユニット　SoftMax

最先端のCNNと比べるとだいぶしょぼいですが、これでも立派なCNNです。10分前後で30epochできます。バッチ標準化は訓練のスピードアップを図るために途中に挿入するレイヤーで、このくらいの浅さだとあまり効果はないかもしれませんが、深い学習では特に有効です。バッチ標準化あり・なし両方で試してみました。

追記：バッチ標準化は、活性化関数の前に挿入するのが一般的だそうです。活性化関数の前に挿入したために効果が薄くなったのだと思います。

モデルの部分以外はディープニューラルネットワークと同じです。

from keras.layers import Dense, Conv2D, MaxPool2D, Activation, Flatten, BatchNormalization

# モデル
# CONV -> RELU -> MAXPOOL
model = Sequential()
model.add(Conv2D(10, (3, 3), strides=(1, 1), input_shape=x_train.shape[1:]))
model.add(Activation("relu"))
model.add(MaxPool2D((3, 3)))

# CONV -> RELU -> BN -> Flatten
model.add(Conv2D(20, (3, 3), strides=(1, 1)))
model.add(Activation("relu"))
model.add(BatchNormalization(axis=3))
model.add(Flatten())

# Softmax
model.add(Dense(10, activation="softmax"))

model.summary()の結果は以下の通りです。

_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
conv2d_1 (Conv2D)            (None, 30, 30, 10)        280
_________________________________________________________________
activation_1 (Activation)    (None, 30, 30, 10)        0
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 10, 10, 10)        0
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 8, 8, 20)          1820
_________________________________________________________________
activation_2 (Activation)    (None, 8, 8, 20)          0
_________________________________________________________________
batch_normalization_1 (Batch (None, 8, 8, 20)          80
_________________________________________________________________
flatten_1 (Flatten)          (None, 1280)              0
_________________________________________________________________
dense_1 (Dense)              (None, 10)                12810
=================================================================
Total params: 14,990
Trainable params: 14,950
Non-trainable params: 40
_________________________________________________________________

だいぶディープラーニングらしくなってきました。パラメーターの数に注目しましょう。全結合層だけの場合はパラメーターが250万もありましたが、畳み込みを入れた場合はたった1.5万です。しかもこっちのほうが訓練が速くて精度が出ます。

出力

# BatchNormあり、epoch=30
Elapsed[s] :  848.2327120304108
10000/10000 [==============================] - 3s 283us/step
train accuracy : 0.70732
test accuracy : 0.6358

# BatchNormなし、epoch=30
Elapsed[s] :  723.7259016036987
10000/10000 [==============================] - 2s 225us/step
train accuracy : 0.72154
test accuracy : 0.6568

コード全体：https://gist.github.com/koshian2/47e5f1d2c832bdb16bd1beefbf20100d

バッチ標準化あり、なしともに10～5分で訓練精度70%、テスト精度65%前後を達成できました。一概に比較していいのかどうかわかりませんが、畳み込みなしの場合は20分以上かかってテスト精度53%だったので、畳み込みをニューラルネットワークで使うと精度の向上（誤差を速く収束させる）にとても有効なことがわかります。

今回はモデルが浅く、訓練も短かったのでバッチ標準化ないほうが良かったですが、深くまたは長く訓練させる場合は有効になることが多いです。

参考：https://qiita.com/dsanno/items/ad84f078520f9c9c3ed1

ではなぜ、畳み込み（エッジ検出）を使うとSVMでは精度が落ち、CNNでは精度が上がったかのかというと、これは自分の想像ですが、畳み込みを使うことでより効率よく画像のデータ構造を伝達できたからだと思います。SVM（今回やっているのは線形カーネル限定）の場合、多層、つまり非線形の伝達というのがありません。ニューラルネットワークにすると非線形の伝達はできますが、全結合の場合、座標、チャンネル問わず1つのベクトルに組み込んでしまうので、最初から全結合だけで行くと伝達の効率が悪いのだと思います。
例えば、全結合の場合だと(1,1)のピクセルに対して、(0,0)～(31,31)の各チャンネルに対して全ての結合を貼っています。でも(1,1)のピクセルと(31,31)のピクセルの関係ってほとんど意味ないですよね。(1,1)のピクセルとの関係を見たかったら、その周囲の(0,0)や(1,0)といったピクセルを見たほうが意義がありますよね。一方で畳み込み層の場合は、カーネル（エッジ検出フィルター）以外の結合を見ません。例えば、(1,1)を起点にカーネル3の畳み込みをする場合は、(1,1)～(3,3)までの結合を見て、それ以外の結合を切り捨てます。全結合に対して「疎な結合」なのが畳み込みニューラルネットワークの特徴です。

また畳み込みフィルターの間でパラメーターを共有するため、エッジの検出というどの位置で切り取っても共通の処理を一本化し、効率よく特徴量を検出することができます。つまり、畳み込み層がやっているのは、エッジの検出といった低レベルの特徴量を、何が鳥で何が自動車であるかといった高レベルの特徴量にマッピングしていることにほかならないのです。生の画像という低レベルの特徴量から全結合をするより、エッジを検出しある程度どういうものかを解釈させてから全結合をしたほうが効率いいですよね。全結合のみのDNNの場合、epoch15・697秒でテスト精度52%でしたが、CNNの場合epoch30・723秒でテスト精度65%出ています。ほぼ同じ処理時間でここまで精度が上がっているので、畳み込みによる特徴量検出が明らかに有利に働いていると言えるでしょう。

このほかパラメーターの数が減ったせいで、メモリ使用量も若干減って、全結合が1.66GB→CNNが1.6GBになりました。200万削ったところで仮に64ビット変数使ったところで16MB減る感じなので、ほぼ誤差みたいなもので、入力画像が32×32だとメモリ使用量に対する係数の割合よりも訓練データのほうが大きいですが、例えば入力画像が256×256になると256×256×3→128×128×10という全結合をしただけで、係数1個あたり8バイトすると約257GB必要です。これではいくら訓練データを減らしても訓練するのは事実上不可能です。したがって、係数のパラメーター数というのもある程度意識する必要があります。

##VGG16からの転移学習
さて、より簡単に精度を上げる方法として**転移学習（Transfer Learning）**というものがあります。これはすでに訓練済みの似た問題（同一ではないのがポイント）のモデルを、そのままスライドしてエッジ検出などの共通の部分を訓練済みとして使ってしまうというとても強力な方法です。

Kerasには訓練済みのVGG16他様々なモデルがあります。VGG16は比較的古いモデルなのですが、入力画像の最小解像度が48×48からいけるので（畳み込みの性質上、どうしても最小解像度の制約がつきます）、データをオンメモリに置いておきやすいのです。今回はやりませんが、データを全部メモリにおかない方法もあるそうです。

転移学習として、(1)VGG16のモデルを読み込んで訓練不可能（layer.trainable=False）として全結合以降のモデルを追加する方法、こちらは転移学習の正攻法です。次に、これを転移学習といっていいのかはわかりませんが、(2)VGGの予測結果をある種のエンコード²としてニューラルネットワーク(3)SVMに食わせる方法を試してみます。(1)はそこそこ時間はかかりますが、(2)(3)はかなり速いです。(2)(3)はCPUでも全然いけます。

###1.VGG16の転移学習
VGG16はkeras.applications.vgg16から使うことができます。使い方は簡単で、

# VGG16の読み込み
base_model = VGG16(include_top=False, input_shape=x_train.shape[1:])
# 転移学習用にVGGを訓練不可にする
for layer in base_model.layers:
    layer.trainable = False

コード全体：https://gist.github.com/koshian2/7a261cfe2ac198ebd41ccb32333c6653

とinclude_top=Falseとすると全結合層を除外して読み込んでくれます。VGGの係数を全てアップデートしないようにします（最後の数層のみ訓練可能にするという方法もあります。特にこれが正解というわけではないのでいろいろ試してみてください）。全結合層を普通のニューラルネットワークと同じように定義すればいいです。

# Flatten以降を作る
top_model = Sequential()
top_model.add(Flatten(input_shape=base_model.output_shape[1:]))
top_model.add(Dense(100, activation="relu"))
top_model.add(Dense(10, activation="softmax"))

# モデルを結合する
model = Model(input=base_model.input, output=top_model(base_model.output))

これでOKです。ちなみにこんなモデル。VGG16の部分を「訓練しない」設定にしたので、パラメーターが1492万あっても大多数がNon-trainable paramsであることが確認できます。

_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
input_1 (InputLayer)         (None, 64, 64, 3)         0
_________________________________________________________________
block1_conv1 (Conv2D)        (None, 64, 64, 64)        1792
_________________________________________________________________
block1_conv2 (Conv2D)        (None, 64, 64, 64)        36928
_________________________________________________________________
block1_pool (MaxPooling2D)   (None, 32, 32, 64)        0
_________________________________________________________________
block2_conv1 (Conv2D)        (None, 32, 32, 128)       73856
_________________________________________________________________
block2_conv2 (Conv2D)        (None, 32, 32, 128)       147584
_________________________________________________________________
block2_pool (MaxPooling2D)   (None, 16, 16, 128)       0
_________________________________________________________________
block3_conv1 (Conv2D)        (None, 16, 16, 256)       295168
_________________________________________________________________
block3_conv2 (Conv2D)        (None, 16, 16, 256)       590080
_________________________________________________________________
block3_conv3 (Conv2D)        (None, 16, 16, 256)       590080
_________________________________________________________________
block3_pool (MaxPooling2D)   (None, 8, 8, 256)         0
_________________________________________________________________
block4_conv1 (Conv2D)        (None, 8, 8, 512)         1180160
_________________________________________________________________
block4_conv2 (Conv2D)        (None, 8, 8, 512)         2359808
_________________________________________________________________
block4_conv3 (Conv2D)        (None, 8, 8, 512)         2359808
_________________________________________________________________
block4_pool (MaxPooling2D)   (None, 4, 4, 512)         0
_________________________________________________________________
block5_conv1 (Conv2D)        (None, 4, 4, 512)         2359808
_________________________________________________________________
block5_conv2 (Conv2D)        (None, 4, 4, 512)         2359808
_________________________________________________________________
block5_conv3 (Conv2D)        (None, 4, 4, 512)         2359808
_________________________________________________________________
block5_pool (MaxPooling2D)   (None, 2, 2, 512)         0
_________________________________________________________________
sequential_1 (Sequential)    (None, 10)                205910
=================================================================
Total params: 14,920,598
Trainable params: 205,910
Non-trainable params: 14,714,688
_________________________________________________________________

VGG16は入力画像が48×48以上という制約があるので、32×32のCIFAR-10はリサイズする必要があります。このためにopencv入れるのもなんかバカバカしかったので出力が64×64のNearest Neighbor法を自分で実装しました。仕組みは簡単で、32×32の(0,0)のピクセルを64×64の(0,0),(0,1),(1,0),(1,1)にコピーするだけです。

# データの読み込み
(x_train_orig, y_train), (x_test_orig, y_test) = cifar10.load_data()
# 小数化
x_train_orig = x_train_orig / 255.0
x_test_orig = x_test_orig / 255.0
# データ数
m_train, m_test = x_train_orig.shape[0], x_test_orig.shape[0]
# yをOneHotVector化
y_train, y_test = to_categorical(y_train), to_categorical(y_test)
# VGG16に読み込めるように32x32→64x64にリサイズ
x_train, x_test = np.zeros((m_train, 64, 64, 3), dtype="float"), np.zeros((m_test, 64, 64, 3), dtype="float")
# Nearest-Neighbor
for i in range(x_train_orig.shape[1]):
    for j in range(x_train_orig.shape[2]):
        x_train[:, i*2, j*2, :] = x_train_orig[:, i, j, :]
        x_train[:, i*2, j*2+1, :] = x_train_orig[:, i, j, :]
        x_train[:, i*2+1, j*2, :] = x_train_orig[:, i, j, :]
        x_train[:, i*2+1, j*2+1, :] = x_train_orig[:, i, j, :]
        x_test[:, i*2, j*2, :] = x_test_orig[:, i, j, :]
        x_test[:, i*2, j*2+1, :] = x_test_orig[:, i, j, :]
        x_test[:, i*2+1, j*2, :] = x_test_orig[:, i, j, :]
        x_test[:, i*2+1, j*2+1, :] = x_test_orig[:, i, j, :]
# メモリばかぐいするのでオリジナルを解法
x_test_orig, x_train_orig = None, None

リサイズした画像がメモリ6～7GB取るんですよね。ここは改良余地ありそうです。あとは訓練させるだけです。

# コンパイル
model.compile(optimizer=Adam(), loss="categorical_crossentropy", metrics=["accuracy"])

# フィット
history = model.fit(x_train, y_train, batch_size=64, epochs=2).history
# 経過時間
print("Elapsed[s] : ", time.time() - start_time)
# テスト精度
test_eval = model.evaluate(x_test, y_test)
print("train accuracy :", history["acc"][-1])
print("test accuracy :", test_eval[1])
# 訓練誤差のプロット
plt.plot(range(len(history["loss"])), history["loss"], marker=".")
plt.show()

さすがにこれはVGG16が重いモデルなので相当時間かかります。CPUだと1epochに40分近くかかりました。とりあえず2epochした結果がこちら。1時間10分です。

出力

# 2 epoch
Elapsed[s] :  4225.965629577637
10000/10000 [==============================] - 419s 42ms/step
train accuracy : 0.70494
test accuracy : 0.6898

思い切って25epochやってみました。15時間半かかって訓練精度は9割超えしましたが、テスト精度はほとんど変わらずにオーバーフィッティングしただけでした。もっと前のレイヤーまで訓練させないとだめですね。

出力

# 25 epoch
#acc: 0.9172
#Elapsed[s] :  55869.90407681465
#10000/10000 [==============================] - 459s 46ms/step
#train accuracy : 0.91724
#test accuracy : 0.6987

とりあえず正攻法の転移学習でテスト精度7割弱、訓練精度は頑張れば9割以上行けることがわかりました。深入りはしませんがオーバーフィッティングは極端な話データの数で殴ればいいので、まずは9割出たことを喜びましょう。

###2. エンコードとしての転移学習
1でやった方法は転移学習としては正攻法なのですが、実はだいぶ無駄な計算をしています。なぜなら、VGG16の係数はずっと固定だからです。どういうことかというと、

入力画像　→　[VGG16(係数固定)]　→　[NN(訓練)]　→　出力

入力→VGG16のまでは、訓練していても値が変わらないので。この方法は使い所が限られるのですが、仮にVGG16の係数を全て固定するなら、入力画像に対するVGG16の出力の結果をファイルかなにかに保存しておいて、その出力結果を普通のニューラルネットワークに食わせるというのができます³。つまりここでのVGG16はどちらかというと「エンコード」です。これを転移学習と言っているサイトもありますが、自分は転移学習の正攻法はあくまで1の方法だと思います。ただ、めちゃくちゃ速いので費用対効果はとても高いと思います。

なぜ使い所が限られるかというと、例えば15層のモデルを転移学習するときに、13層までの係数を固定する場合は13層での出力を求めればいいのでOKですが、12層までと14層を固定、つまり13層と15層を訓練させたいときはこの方法は使えません。またエッジ検出などの浅い層をチューニングしたい場合もこの方法はほとんど意味がありません。

まずはエンコード部分から。

import numpy as np
import matplotlib.pyplot as plt
import time
import os
from keras.applications.vgg16 import VGG16
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.optimizers import Adam
from keras.datasets import cifar10
from keras.utils.np_utils import to_categorical

start_time = time.time()
# リサイズ
def resize(images):
    out_img = np.zeros((images.shape[0] ,64, 64, 3))
    # Nearest Neighbor
    for i in range(images.shape[1]):
        for j in range(images.shape[2]):
            out_img[:, i*2, j*2, :] = images[:, i, j, :]
            out_img[:, i*2, j*2+1, :] = images[:, i, j, :]
            out_img[:, i*2+1, j*2, :] = images[:, i, j, :]
            out_img[:, i*2+1, j*2+1, :] = images[:, i, j, :]
    return out_img

## 事前にVGG16でエンコードしてファイルに保存
if os.path.exists("vgg_encode.npz"):
    file = np.load("vgg_encode.npz")
    enc_train, y_train, enc_test, y_test = file["enc_train"], file["y_train"], file["enc_test"], file["y_test"]
else:
    # データの読み込み
    (x_train_orig, y_train), (x_test_orig, y_test) = cifar10.load_data()
    # 小数化
    x_train_orig = x_train_orig / 255.0
    x_test_orig = x_test_orig / 255.0
    # データ数
    m_train, m_test = x_train_orig.shape[0], x_test_orig.shape[0]
    # yをOneHotVector化
    y_train, y_test = to_categorical(y_train), to_categorical(y_test)

    # VGG16の読み込み
    vgg = VGG16(include_top=False, input_shape=(64, 64, 3))

    # 普通の転移学習だと時間がかかるので一旦エンコードしてしまう
    enc_train = vgg.predict(resize(x_train_orig))
    enc_test = vgg.predict(resize(x_test_orig))

    # ベクトル化（フラット化しているのと同じ）
    enc_train, enc_test = enc_train.reshape(m_train, -1), enc_test.reshape(m_test, -1)
    # ファイルに保存
    np.savez("vgg_encode", enc_train=enc_train, y_train=y_train, enc_test=enc_test, y_test=y_test)

保存するのはVGG16の入力画像に対するフラットニングする前の最終層の値です。include_top=Falseなので、(2, 2, 512)の値が出力されます。この値はpredict()で計算できます。どうせフラットニングにしてしまうので、Numpyのresizeでベクトル化してこれを保存します。

以降のモデルは次の通りです。畳み込みニューラルネットワークの問題を、入力が2048次元のベクトルの普通のニューラルネットワークの問題に置き換えることができました。

# 転移学習部分のモデル
print(enc_train.shape)
model = Sequential()
model.add(Dense(512, activation="relu", input_shape=enc_train.shape[1:]))
model.add(Dropout(0.5))
model.add(Dense(100, activation="relu", input_shape=enc_train.shape[1:]))
model.add(Dense(10, activation="softmax", input_shape=enc_train.shape[1:]))

あとはいつもの通り。学習率を調整して0.01にします。

# コンパイル
model.compile(optimizer=Adam(lr=0.01), loss="categorical_crossentropy", metrics=["accuracy"])

コード全体：https://gist.github.com/koshian2/a7fc6cf1a8ad07805fbd973f6a8308c8

正則化のためにドロップアウトを入れてみました。とても良い感じ。たった30分で精度7割出ます。事前計算して高速化できるので、30分で100epochできます。

出力

Elapsed[s] :  1907.3146982192993
10000/10000 [==============================] - 1s 85us/step
train accuracy : 0.71752
test accuracy : 0.6928

ドロップアウトなしの場合はこちら。ちょっとオーバーフィッティングしていますね。

出力

Elapsed[s] :  1753.4181559085846
10000/10000 [==============================] - 1s 73us/step
train accuracy : 0.81536
test accuracy : 0.6797

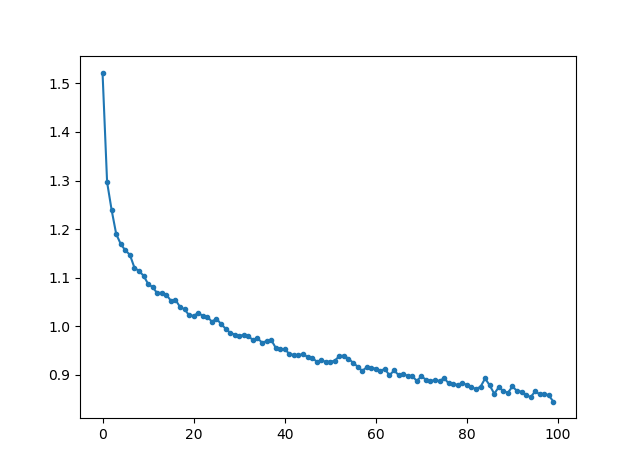
ドロップアウトありの場合の訓練誤差プロットは以下の通りです。

誤差プロットはまだ下がりそうですが、300周させてもあまり変わりませんでした。

###3.VGG16＋SVM
先程の発想を応用すると、VGG16でエンコードした結果をSVMに食わせるということができます。やってみます。先に2.を実行済みでvgg_encode.npzが存在するものとします。

import numpy as np
import time
from sklearn.svm import LinearSVC

start_time = time.time()
# 事前にCIFAR10_VGG16_fast.pyを実行済みとする
file = np.load("vgg_encode.npz")
enc_train, y_train, enc_test, y_test = file["enc_train"], file["y_train"], file["enc_test"], file["y_test"]
# ノルムで標準化
enc_train = enc_train / np.linalg.norm(enc_train, ord=2, axis=1, keepdims=True)
enc_test = enc_test / np.linalg.norm(enc_test, ord=2, axis=1, keepdims=True)
# One-hot-vectorを戻す
y_train = np.sum(y_train * np.arange(10), axis=1)
y_test = np.sum(y_test * np.arange(10), axis=1)

# サポートベクトルマシン
svc = LinearSVC()
svc.fit(enc_train, y_train)
print("Elapsed[s] : ", time.time() - start_time)
print("Train :", svc.score(enc_train, y_train))
print("Test :", svc.score(enc_test, y_test))

エンコードしたファイルではYはOne Hotベクトルとして記録されているので、ラベルの値に戻す作業をしています。結果は以下のとおりです。

出力

Elapsed[s] :  26.870912075042725
Train : 0.73596
Test : 0.7074

たった30秒でテスト精度70%越えてしまいました。ディープラーニングとは何だったんでしょう。SVMに始まり、SVMに終わりました。

###4.よりチューニングされたモデル
実はVGG16をCifar10用にチューニングしたモデルというのはすでにあって、GitHubに上がっていました。

これによるとValidation accuracyが93.56%も出るそうです。すごいですね。係数をダウンロードして使えばいいだけです。

##まとめ
これまでの結果をまとめると次のようになります。

アルゴリズム	ライブラリ	実行秒	訓練精度	テスト精度	注
ロジスティック回帰	sklearn	329.3	42.00%	40.72%
SVM	sklearn	275.1	45.12%	40.62%	[1]
ランダムフォレスト	sklearn	18.3	43.40%	37.17%	[2]
グレースケール＋SVM	sklearn	91.3	33.13%	29.01%
エッジ検出＋SVM	sklearn	1282.1	26.96%	21.53%
エッジ検出＋プーリング＋SVM	sklearn	1036.9	22.65%	22.22%
ニューラルネットワーク（全結合）	Keras	697.3	57.60%	52.31%	[3]
畳み込みニューラルネットワーク	Keras	723.7	72.15%	65.68%	[4]
VGG16転移学習（epoch=2)	Keras	4226.0	70.49%	68.98%	[5]
VGG16転移学習（epoch=25)	Keras	55869.9	91.72%	69.87%
VGG16→エンコード→NN	Keras	1907.3	71.75%	69.28%	[6][7]
VGG16→エンコード→SVM	Keras+sklearn	26.9	73.60%	70.74%	[7]

(注)

• 計算は全てCPU。Kerasではマルチコアの並列処理が行われるが、sklearnではデフォルトのシングルコアで計算している。4コアのCPUであるので、Kerasの実行時間とsklearnの実行時間にはスケールで2～4倍の差がある。
• [1]カーネルなし。サンプルのベクトルのノルムを1として標準化。これを入れないと1時間ぐらいかかる
• [2]max-depth=8としてオーバーフィッティングを解消
• [3]Input:3072→ReLU:768→ReLU:192→Softmax:10, epoch=15
• [4]Conv2d:x10(f=3, s=1)→ReLU→MaxPool(f=3, s=3)→Conv2d:x20(f=3, s=1)→ReLU→MaxPoo→FC:1280→Softmax:10
• [5]VGG16(訓練なし）→FC:2048→ReLU:100→Softmax:10
• [6]入力データ→VGG16でpredict→結果をファイルに保存、Input:2048→ReLU:512→Dropout0.5→ReLU:100、Softmax:10, epoch=100
• [7]エンコードそのものに40分近くかかるが、ファイルに保存すれば結果を使いまわしできる

冒頭の疑問は、「なぜ畳み込みニューラルネットワークが必要なのか」でしたが、畳み込みを使うと画像の特徴量を上手く検出できるからというのが答えです。エッジ検出＋SVMの例で見たように、CNNで使われているエッジ検出やプーリングそのものには精度の向上性はありません。むしろ単体で使うと精度が落ちます。しかし、これらをニューラルネットワーク上で使うと**「疎な結合」「パラメーターの共有」**というCNNの2つの特徴により、特徴量の検出を容易にし、全結合の場合よりも学習の計算コストを減らしよりスピードアップさせることができます。これが畳み込みニューラルネットワークのすごさです。

そして、畳み込みニューラルネットワークでは転移学習がとても強力に機能することが確認できました。モデルが深くなりがちなので、ニューラルネットワーク自体の計算コストはとても高いですが、チューニング済みのモデルから転移学習をすることで大きく計算コストをカットすることが可能です。転移学習の1つとして、ディープラーニングの途中結果を取り出すことで（画像を特徴量のベクトルにマッピングすることで）、SVMといった従来の機械学習アルゴリズムとも相性が良いこともわかりました。使い所が限られますが、上手く使うととても便利だと思います。

1. 本当は訓練、テストデータのほかに訓練データを分割して開発データを用意してハイパーパラメーターをチューニングする必要がありますが、今回はそこまで厳密にはやらなくていいかなと ↩

2. ニューラルネットワークをエンコードとして、別の予測器に食わせるのは例えば顔認証で使われているそうです　https://www.coursera.org/learn/convolutional-neural-networks/lecture/xTihv/face-verification-and-binary-classification ↩

3. VGG16の出力結果をキャッシュすることで計算を高速化する、アルゴリズムにおける「メモ化」の発想です ↩