Coursera Machine LearningをPythonで実装 - [Week9]異常検知、協調フィルタリング

最終回です。今回は異常検知（外れ値の検出）と協調フィルタリング（レコメンデーションシステム）です。自分の環境では既存のライブラリと相性が悪かったので、全て自分で実装しました。協調フィルタリングのほうは長くなってしまいもうちょっと上手いやり方あると思いますが、異常検知のほうはこの方法が速いと思います。

コード gistからダウンロードできます
* 異常検知　https://gist.github.com/koshian2/3aaf85fcfc137b6ffe63b63e9983a6c0
* 協調フィルタリング　https://gist.github.com/koshian2/3012c9973a0a1bf664a62f12deff2349

これまでの目次

• Coursera Machine LearningをPythonで実装 - [Week2]単回帰分析、重回帰分析
• Coursera Machine LearningをPythonで実装 - [Week3]ロジスティック回帰
• Coursera Machine LearningをPythonで実装 - [Week4]ニューラルネットワーク(1)
• Coursera Machine LearningをPythonで実装 - [Week5]ニューラルネットワーク(2)
• Coursera Machine LearningをPythonで実装 - [Week6]正則化、Bias vs Variance
• Coursera Machine LearningをPythonで実装 - [Week7]サポートベクターマシン（SVM）
• Coursera Machine LearningをPythonで実装 - [Week8]k-Means, 主成分分析（PCA）

◎異常検知を自分で実装

Scikit-learnに組み込みのEllipticEnvelopeという異常検知用のクラスがあるのですが、GridSearchCVの相性が悪くてどうも自分で実装したほうがはるかに速いことがわかったので、自分で実装するほうを推奨です。EllipticEnvelopeをcontaminationの値を100分割してGridSearchCVで回すと10秒～20秒かかるのですが、この自分で実装する方法だとεを1000分割しても1秒かからずに終わります。（分散や平均をfit()ごとに再計算しててキャッシュしていないから遅い？）なんかうまい方法あったら教えてください。ちなみにGridSearchCVを使う場合は、scoringを"f1"ではなく"f1_micro"にするとエラー出ません。

Scipy.statsに多変量正規分布の確率密度関数があるのでこれを使いましょう。あとは単純です。

1.データの読み込み

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
from scipy.stats import multivariate_normal
from sklearn.metrics import f1_score

## 1.データの読み込み
def load_data(filename):
    data = loadmat(filename)
    return np.array(data['X']), np.array(data['Xval']), np.ravel(np.array(data['yval']))
X, Xval, yval = load_data("ex8data1.mat")
# データのプロット
def plot_data():
    plt.plot(X[:,0], X[:, 1], "bx")
    plt.xlabel("Latencey (ms)")
    plt.ylabel("Throughput (mb/s)")
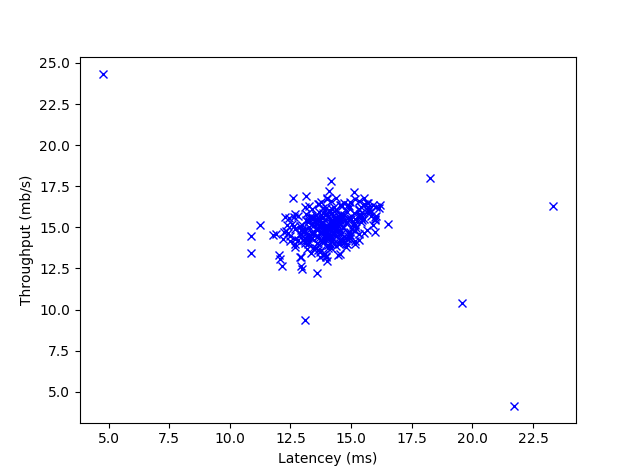
plot_data()
plt.show()

サーバーの遅延に関するデータのようです。

2.データの統計量の推定

データが正規分布になると仮定して、パラメーターを推定します。

## 2.データの統計量を推定
def estimate_gaussian(X):
    mu = np.mean(X, axis=0)
    sigma2 = np.var(X, axis=0)
    return mu, sigma2
mu, sigma2 = estimate_gaussian(X)
# 多変量正規分布の確率密度関数を計算
# 分散のベクトルを共分散行列に変形（対角要素＝分散とする）
cov_matrix = np.diag(sigma2)
# （自分で定義してもいいが、scipy.stats.multivariate_normalを使うと楽）
p = multivariate_normal.pdf(X, mean=mu, cov=cov_matrix)
# 可視化
def visualize_fit(X, mu, sigma2):
    plot_data()
    X1, X2 = np.meshgrid(np.arange(0, 35, 0.5), np.arange(0, 35, 0.5))
    Z = multivariate_normal.pdf(np.c_[np.ravel(X1), np.ravel(X2)], mean=mu, cov=np.diag(sigma2))
    Z = Z.reshape(X1.shape)
    if not np.isinf(np.sum(p)):
        plt.contour(X1, X2, Z, levels=10**np.arange(-20, 0, 3, dtype="float"))
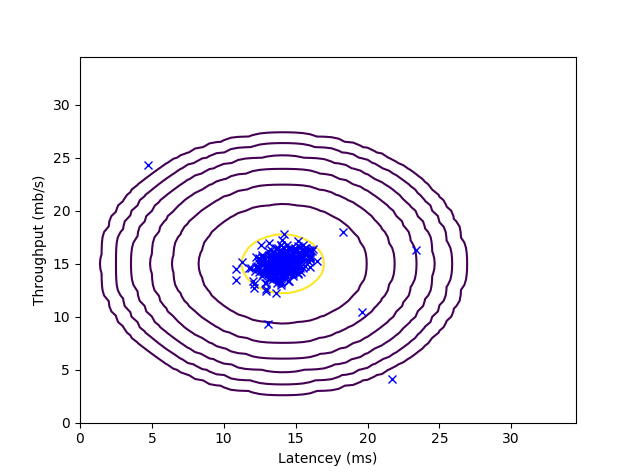
visualize_fit(X, mu, sigma2)
plt.show()

多変量正規分布は自分で書くの面倒くさいのでscipy.stats.multivariate_normalを使いましょう。統計でよく使うので、他言語でも統計関連のパッケージ探せば多分あります。ここでは、分散共分散行列の対角成分以外を0として（つまり変数間は全て独立であると仮定して）、np.var()で計算した分散を分散共分散行列の対角成分に代入します。分散共分散行列の対角成分は分散に等しいので。この独立の仮定は、1変数の正規分布を積の形でつなげたものと等しくなります。
ちなみにパラメーター間の相関を加味したい場合は、分散の導出にnp.varではなくnp.covを使います。これでダイレクトに分散共分散行列が計算できます。

3.外れ値を探す

εを推定します。外れ値の定義は、何らかの確率密度関数p（ここでは多変量正規分布としますが）を用意して、$p(X)<\epsilon$のときに外れ値と定義します。
ここでεはハイパーパラメーターになるので、交差検証データからF1スコアを最大化するようなεを探します。F1スコアの計算は組み込み使うと少し楽できます。

## 3.外れ値を探す
# 交差検証データに対するpvalを計算
pval = multivariate_normal.pdf(Xval, mean=mu, cov=cov_matrix)
# しきい値を選択
def select_threshold(yval, pval):
    best_epsilon, best_f1 = 0, 0
    steps = np.linspace(np.min(pval), np.max(pval), 1000)
    for epsilon in steps:
        pred_positive = pval < epsilon
        f1 = f1_score(yval, pred_positive)
        if f1 > best_f1:
            best_f1, best_epsilon = f1, epsilon
    return best_epsilon, best_f1
# εはハイパーパラメーターなので交差検証データに対してフィットさせる
epsilon, f1 = select_threshold(yval, pval)
print("Best epsilon found using cross-validation:", epsilon)
print("Best F1 on Cross Validation Set:", f1)
print("   (you should see a value epsilon of about 8.99e-05)")
print("   (you should see a Best F1 value of  0.875000)\n")
# 外れ値を探す
outliers = p < epsilon
# 外れ値のプロット
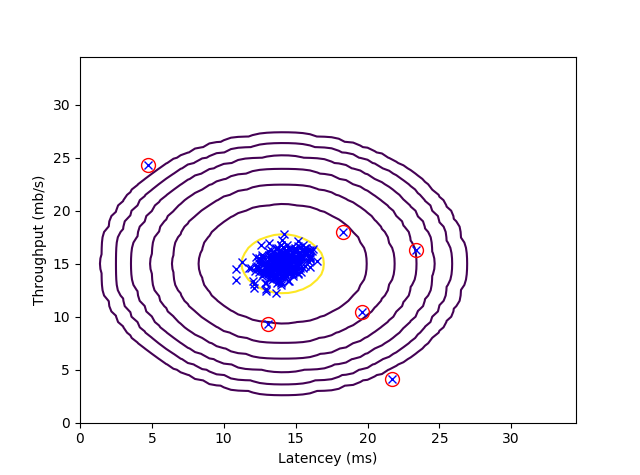
visualize_fit(X, mu, sigma2)
plt.plot(X[outliers, 0], X[outliers, 1], "ro", markerfacecolor="none", linewidth=2, markersize=10)
plt.show()

εはテストデータではなく、交差検証データにフィットさせるようにしましょう。

出力

Best epsilon found using cross-validation: 8.9998526319e-05
Best F1 on Cross Validation Set: 0.875
   (you should see a value epsilon of about 8.99e-05)
   (you should see a Best F1 value of  0.875000)

いい感じに外れ値が選ばれました。

4.多次元の外れ値

今度は1000×11の訓練データを読み込んでみます。特に何も変わりません。

## 4.多次元の外れ値
# データの読み込み
X, Xval, yval = load_data("ex8data2.mat")
# 統計量の推定
mu, sigma2 = estimate_gaussian(X)
# 訓練データ
p = multivariate_normal.pdf(X, mean=mu, cov=np.diag(sigma2))
# 交差検証データ
pval = multivariate_normal.pdf(Xval, mean=mu, cov=np.diag(sigma2))
# しきい値の選択
epsilon, f1 = select_threshold(yval, pval)
print("Best epsilon found using cross-validation: ", epsilon)
print("Best F1 on Cross Validation Set:  ", f1)
print("   (you should see a value epsilon of about 1.38e-18)")
print("   (you should see a Best F1 value of 0.615385)")
print("# Outliers found:", np.sum(p < epsilon))

訓練データをフィットさせると訓練データの11.7%が外れ値として検出されるので、F1スコアはだいぶ下がりますね。

出力

Best epsilon found using cross-validation:  1.3786074982e-18
Best F1 on Cross Validation Set:   0.615384615385
   (you should see a value epsilon of about 1.38e-18)
   (you should see a Best F1 value of 0.615385)
# Outliers found: 117

◎協調フィルタリング（レコメンデーション）を自分で実装

協調フィルタリングのパッケージsurpriseというのがあるのですが、自分の環境（VisualStudio2017）では

    building 'surprise.similarities' extension
    error: Microsoft Visual C++ 14.0 is required. Get it with "Microsoft Visual C++ Build Tools": http://landinghub.visualstudio.com/visual-cpp-build-tools

とエラーが出てインストールできませんでした。C++の開発環境やBuildToolを入れてもエラー消えなかったので残念ながら諦めました。そこまで複雑なアルゴリズムではないので、1から自分で実装します。

1.映画のデータの読み込み

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat

## 1.映画のレーティングのデータの読み込み
def load_movies():
    data = loadmat("ex8_movies.mat")
    return np.array(data['Y']), np.array(data['R'])
Y, R = load_movies()
# 1番目の映画の平均レート
print("Average rating for movie 1 (Toy Story):", np.mean(Y[0, R[0, :]]), "/ 5\n")
# データの可視化
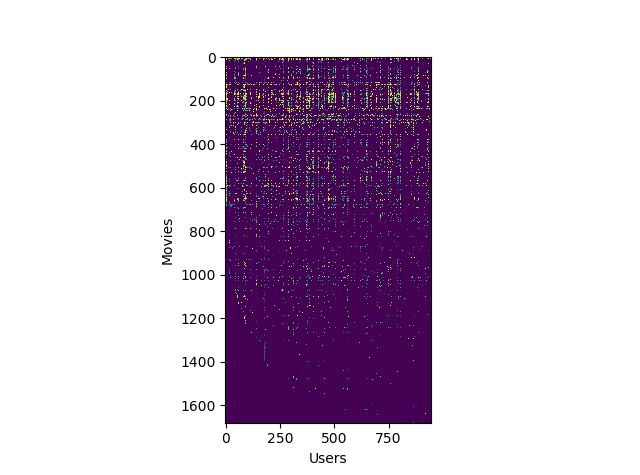
plt.imshow(Y)
plt.xlabel("Users")
plt.ylabel("Movies")
plt.show()

Yには1682本分の映画のレーティングが943人分入っており、0～5の値の1682×943の行列になっています。Rには各映画、各ユーザーに対して、レート付けされたかのフラグが0か1かで入っており、Yと同じく1682×943の行列になっています。MovieLens 100k Datasetというデータが出処だそうです。試しにID=1の映画（トイ・ストーリー）の平均レーティングを出してみます。

出力

Average rating for movie 1 (Toy Story): 4.52067868505 / 5

Yを画像としてプロットすると次のようになります。

2.協調フィルタリングのコスト関数

コスト関数のテストをするために、X,Thetaの計算済みの値を読み込みます。本来XとThetaは最適化によって計算します。このXとThetaが何かというと、映画単位、ユーザー単位での特徴量のデータです。映画単位の特徴量とは、感覚的な理解では、例えば恋愛映画やアクション映画といった映画のジャンルというのがこれに当たります。ここでは特徴量の数を10としています。

ただ、特徴量自体がデータとして与えるものではなく、最適化の過程で「ユーザーのレーティングからもっともらしく計算されるもの」なので、どちらかというとニューラルネットワークの隠れ層に近いイメージなのかもしれません。もっともらしく計算した特徴量から、ユーザーが見ていない映画に対してもっともらしくレーティングを推定することがこの問題の目的なので。

## 2.協調フィルタリングのコスト関数
# 事前に訓練済みの値を読み込み
def load_movie_params():
    data = loadmat("ex8_movieParams.mat")
    return np.array(data['X']), np.array(data['Theta']), data['num_users'], data['num_movies'], data['num_features']
X, Theta, num_users, num_movies, num_features = load_movie_params()

# コスト関数を速く走らせるために一旦値を減らす（これでX,Y,Rがどんな構造かわかるはず）
num_users, num_movies, num_features = 4, 5, 3
X = X[:num_movies, :num_features]
Theta = Theta[:num_users, :num_features]
Y = Y[:num_movies, :num_users]
R = R[:num_movies, :num_users]

# コスト関数
def confi_costfunc(param, Y, R, lambda_):
    # 最適化用にparam=[X, Theta]としておく
    X, Theta = param
    # 推定値との誤差（R[i,j]==1つまり、レートが与えられているもののみ計算するのが重要）
    diffs = (np.dot(X, Theta.T) - Y) * R
    # コスト関数
    J = np.sum(diffs ** 2) / 2 + lambda_ / 2 * (np.sum(Theta ** 2) + np.sum(X ** 2))
    # 勾配
    X_grad = np.dot(diffs, Theta) + lambda_ * X
    Theta_grad = np.dot(diffs.T, X) + lambda_ * Theta
    grad = [X_grad, Theta_grad]
    return J, grad
# コスト関数のテスト
J, grad = confi_costfunc([X, Theta], Y, R, 0)
print("Cost at loaded parameters:", J)
print("(this value should be about 22.22)\n")

Xは行に映画、列に特徴量をおいた、映画単位での特徴量のクロス集計で、1682×10の行列になります。Thetaは行にユーザー、列に特徴量をおいた、ユーザー単位でのクロス集計で、943×10の行列になります。

今デバッグ用に分母を少なくしています。これからの流れは、コスト関数の作成→Gradient Checkingをして、コスト関数が正常に動くか確かめる工程が続きます。ニューラルネットワークのときと同じですね。

Cost at loaded parameters: 22.2246037257
(this value should be about 22.22)

3.Gradient Checkingの実装

ニューラルネットワークのときと同じようにGradient Checkingをします。Gradient Checkingとは何かというと、コスト関数で返される勾配が正しいかどうか確認するためのものです。微小な値εを用意して、

$$\frac{J(\Theta+\epsilon)-J(\Theta-\epsilon)}{2\epsilon} $$

という計算をすれば、Jの値だけから勾配を求めることができます（アルゴリズム的にはものすごく効率悪いので、本来は解析的に計算します。あくまでデバッグ用なので）。いまこれを数値的に計算した値とすると、本来コスト関数の中で計算した解析的に計算した値と比較し、それらの相対誤差が限りなく小さくなれば、実装が正しいことがわかります。

## 3.協調フィルタリングのコスト関数の勾配（Gradient Checking）
# Gradient Checking用の関数
def compute_numerical_gradient(Jonly_func, param):
    # コストのみ返す関数をJonly_funcにラップする、paramは[X, Theta]のように配置する
    # paramが3変数以上になっても対応できているはず
    shapes = [x.shape for x in param]
    # 行列の要素数の累積和
    param_size_cumsum = np.append(0, np.cumsum([np.size(x) for x in param]))
    # ベクトルとして格納
    numgrad, pertub = np.zeros(param_size_cumsum[-1]), np.zeros(param_size_cumsum[-1])
    e = 1e-4
    for p in range(param_size_cumsum[-1]):
        pertub[p] = e
        t1, t2 = [], []
        for i in range(len(param)):
            delta_e = pertub[param_size_cumsum[i]:param_size_cumsum[i+1]].reshape(shapes[i])
            t1.append(param[i] - delta_e)
            t2.append(param[i] + delta_e)
        loss1, loss2 = Jonly_func(t1), Jonly_func(t2)
        numgrad[p] = (loss2 - loss1) / (2*e)
        pertub[p] = 0
    # 勾配を配列に戻す
    grad = []
    for i in range(len(param)):
        grad.append(numgrad[param_size_cumsum[i]:param_size_cumsum[i+1]].reshape(shapes[i]))
    return grad
def check_cost_function(lambda_):
    # 小さい問題を作る
    X_t = np.random.rand(4, 3)
    Theta_t = np.random.rand(5, 3)
    Y = np.dot(X_t, Theta_t.T)
    Y[np.random.rand(*Y.shape) > 0.5] = 0
    R = np.zeros(Y.shape)
    R[Y != 0] = 1
    # Gradient Checkingを実行
    X = np.random.standard_normal(X_t.shape)
    Theta = np.random.standard_normal(Theta_t.shape)
    wrap = lambda P : confi_costfunc(P, Y, R, lambda_)[0]
    numgrad = compute_numerical_gradient(wrap, [X, Theta])
    cost, grad = confi_costfunc([X, Theta], Y, R, lambda_)
    # 比較
    diff_m, diff_p = 0, 0
    for n, g in zip(numgrad, grad):
        for nn, gg in zip(np.ravel(n), np.ravel(g)):
            diff_m += (nn - gg) ** 2
            diff_p += (nn + gg) ** 2
            print(nn, gg)
    print("The above two columns you get should be very similar.")
    print("(Left-Your Numerical Gradient, Right-Analytical Gradient)\n")
    diff = np.sqrt(diff_m / diff_p)
    print("If your cost function implementation is correct, then")
    print("the relative difference will be small (less than 1e-9). ")
    print("Relative Difference:", diff, "\n")

ニューラルネットワークのときのコードを改良して、paramの引数が3以上になっても対応できるようにしました。compute_numerical_gradientは別の問題でも使えるはずです。

4.正則化

正則化を行う場合でもコスト関数が正しく動作するか確認します。

## 4.正則化ありの協調フィルタリングのコスト関数
# コスト関数のテスト
J, grad = confi_costfunc([X, Theta], Y, R, 1.5)
print("Cost at loaded parameters (lambda = 1.5):", J)
print("(this value should be about 31.34)\n")

ちょっと足し算が増えただけなので特に問題ないかと思います。行列の計算が頭こんがらがっていきますが、入力と出力の次元を考えるとどういうコードを書けばいいか見えてくることが多いです。

出力

Cost at loaded parameters (lambda = 1.5): 31.3440562443
(this value should be about 31.34)

5.Gradient Checkingを行う

3で実装したGradient Chcekingを実行します。

## 5. GraidientChecking
check_cost_function(1.5)

出力

0.873426679746 0.873426679777
-1.06679537645 -1.06679537646
　　（　　：　中略　　：　　）
-46.4531869345 -46.4531869345
13.2989849779 13.298984978
The above two columns you get should be very similar.
(Left-Your Numerical Gradient, Right-Analytical Gradient)

If your cost function implementation is correct, then
the relative difference will be small (less than 1e-9).
Relative Difference: 1.37148521289e-12

左が数値的に計算した勾配の値、右が解析的に計算した値です。引数の値をランダムにしているので実行するたびに結果は変わりますが、相対誤差（Relative Difference）が極めて小さくなることを確認できればOKです。

実際の問題ではコスト関数の値が本来いくらになるかというのはよくわからないので、コスト関数が正常に動作しているかを確認するにはGradient Checkingぐらいしかないと思います。特に今回のように既存のライブラリが使えなく自分で実装する場合は、必ずやったほうがいいです。

6.新しいユーザーのレーティングを入力

さてここからが本番です。この問題でやりたいことは、ユーザーの入力したレーティングに従って「この映画を良いと評価した人にはこの映画もおすすめです」というレコメンデーション機能を作ることでした。まずは新規ユーザーのレーティングデータを入力します。

## 6.新しいユーザーのレーティングを入力
# 映画のタイトルをロード
with open("movie_ids.txt", "rb") as fp:
    # テキストのデコードがうまくいかないのでバイト単位で読み込む
    movies_list = fp.readlines()
# 自分のレーティングを作る
my_ratings = np.zeros(1682)
# ID=0（トイ・ストーリー[1995]は4とする）
my_ratings[0] = 4
# ID=97（羊たちの沈黙[1991]は2とする）
my_ratings[97] = 2
# 同様にレーティングをつける
my_ratings[[6,11,53,63,65,68,182,225,354]]=3,5,4,5,3,5,4,5,5
print("New user ratings:")
for i in range(len(my_ratings)):
    if my_ratings[i] > 0:
        print("Rated", my_ratings[i], "for", movies_list[i].decode(), end="")

トイ・ストーリー、羊たちの沈黙、フォレスト・ガンプ、ダイ・ハード2といったおなじみの映画が並びます。これらの映画が好き・嫌いな人に、どういう映画が好きか推定し、それをもとに「こういう映画がおすすめですよ」と知らせるのがレコメンデーション機能であり、その1つのアルゴリズムが協調フィルタリングなのです。
余談ですが、Wikipediaの協調フィルタリングで「Excelでもできますよ」と載っているのは、これじゃなくて多分アソシエーション分析のほうなので、それよりかはもう少し難しいアルゴリズムです。これをExcelでやるのはきついと思います。

出力

New user ratings:
Rated 4.0 for 1 Toy Story (1995)
Rated 3.0 for 7 Twelve Monkeys (1995)
Rated 5.0 for 12 Usual Suspects, The (1995)
Rated 4.0 for 54 Outbreak (1995)
Rated 5.0 for 64 Shawshank Redemption, The (1994)
Rated 3.0 for 66 While You Were Sleeping (1995)
Rated 5.0 for 69 Forrest Gump (1994)
Rated 2.0 for 98 Silence of the Lambs, The (1991)
Rated 4.0 for 183 Alien (1979)
Rated 5.0 for 226 Die Hard 2 (1990)
Rated 5.0 for 355 Sphere (1998)

7.モデルの学習

前処理としてレーティングを映画単位で標準化（作品単位の平均でYを引く）します。なぜなら、これをしないとどの作品もレーティング付けしていないユーザーがいた場合、全ての作品のレートが0として推定されてしまうからです。標準化をすることで、そのようなユーザーに対しては、作品の平均値を推定値として与えることができます。
機械学習一般での標準化では、データを平均で引いて標準偏差で割るということをしましたが、今回はどのデータもレーティングが0～5と幅が一定なので、平均で引くだけでOKです。ただし、0～5のデータと0～100のデータが混じっている場合、つまりスケールの異なるデータが混在している場合は標準偏差で割る必要があります。

# データのロード
Y, R = load_movies()
# 新しいユーザーのレーティングを追加
Y = np.c_[my_ratings, Y]
R = np.c_[(my_ratings != 0).astype(int), R]
# レーティングを平均化（未評価の作品に対して平均値が推定されるようにするため）
def normalize_ratings(Y, R):
    m, n = Y.shape
    Ymean = np.zeros(m)
    Ynorm = np.zeros(Y.shape)
    for i in range(m):
        idx = R[i, :] == 1
        Ymean[i] = np.mean(Y[i, idx])
        Ynorm[i, idx] = Y[i, idx] - Ymean[i]
    return Ynorm, Ymean
Ynorm, Ymean = normalize_ratings(Y, R)

初期値はニューラルネットワークのようにランダムの値を与えます。これはSymmetry breakingのためです。全てゼロとして与えてしまうと、ニューラルネットワークと同様に全ての特徴量の係数が等しいと暗黙に仮定してしまうためでしょう。

# 定数
num_users = Y.shape[1]
num_movies = Y.shape[0]
num_features = 10
# 初期値
X = np.random.standard_normal((num_movies, num_features))
Theta = np.random.standard_normal((num_users, num_features))
lambda_ = 10

ここでは面倒くさかったので、最急降下法を自分で実装してしまいましたが、もっと収束の早そうな共役勾配法（fmin_cg）やBFGS（fmin_bfgs）などの組み込み関数で最適化してもいいと思います。これらの関数を使いたい場合は、ΘとXを1つのベクトルに統合して定義する必要があります（その場合はコスト関数の引数の定義も変えたほうがいいかもしれません）。

# 最急降下法
import sys, time, copy
def gradient_descent(initial_params, cost_wrap, eta, maxiter = 100):
    theta_before = initial_params
    for i in range(maxiter):
        J, grad = cost_warp(theta_before)
        theta = copy.deepcopy(theta_before)
        for j in range(len(initial_params)):
            theta[j] = theta[j] - eta * grad[j]
        mes = f"iter = {i}, J = {J}"
        theta_before = theta
        # コンソールを埋め尽くさないように上書きしながら表示
        sys.stdout.write("\r%s" % mes)
        sys.stdout.flush()
    return theta, J
# 最小化するコスト関数
cost_warp = lambda P:confi_costfunc(P, Ynorm, R, lambda_)
# 最急降下法の実行
params, J = gradient_descent([X, Theta], cost_warp, 0.005, maxiter=1000)
# 結果の格納
X, Theta = params

1000回反復させてみましたが、1分少々で結果が出てきます。

出力

iter = 999, J = 38967.901817914864

8.レコメンデーション

結果を表示します。推定値はXとTheta.T（Thetaの転置行列）の内積で求められます。

## 8.レコメンデーション
p = np.dot(X, Theta.T)
my_predictions = p[:, 0] + Ymean
# おすすめ順に降順ソート
idx = np.argsort(my_predictions)[::-1]
print("\n\nTop recommendations for you:")
for i in range(10):
    print("Predicting rating", np.round(my_predictions[idx[i]], 2), "1f for movie", movies_list[idx[i]].decode(), end="")

おすすめトップ10を表示してみます。推定レーティングの高いトップ10を表示しているものです。

出力

Top recommendations for you:
Predicting rating 5.0 1f for movie 1201 Marlene Dietrich: Shadow and Light (1996)
Predicting rating 5.0 1f for movie 814 Great Day in Harlem, A (1994)
Predicting rating 5.0 1f for movie 1122 They Made Me a Criminal (1939)
Predicting rating 5.0 1f for movie 1536 Aiqing wansui (1994)
Predicting rating 5.0 1f for movie 1293 Star Kid (1997)
Predicting rating 5.0 1f for movie 1467 Saint of Fort Washington, The (1993)
Predicting rating 5.0 1f for movie 1653 Entertaining Angels: The Dorothy Day Story (1996)
Predicting rating 5.0 1f for movie 1189 Prefontaine (1997)
Predicting rating 5.0 1f for movie 1599 Someone Else's America (1995)
Predicting rating 5.0 1f for movie 1500 Santa with Muscles (1996)

推定値はレーティング換算でわずかな差なので、順番や作品は収束結果や最適化アルゴリズムによって変わるはずです。

レコメンデーション機能自体そのものは需要があるものですが、作品自体の特徴量という観測できないパラメーターを媒介にして、回帰問題を解くというのは応用範囲が広そうな印象を受けます。これニューラルネットワークだとどう実装するんでしょうね。NNだとあくまで分類問題なので、回帰問題に変えるのは多分何か方法あるはずでしょうが、これがざっくりできてしまうのが協調フィルタリングの強みではないかと思います。

最後に

これでCoursera Machine LearningのPythonでの実装は最後になります。CourseraのMachine Learningのコースはとてもしっかりしていて、これでほぼ基本は抑えられたと思います。Andrew Ng先生の説明がとてもわかりやすいので、英語や数学に特に苦手意識がないのなら、機械学習の入門はほぼこれ一択です。自分もこれを受講して明らかに機械学習に対する視点が変わりました。

今アマゾン情報学・情報科学のベストセラー（5/13時点で1位）になっている本で『scikit-learnとTensorFlowによる実践機械学習』というのがあります。ざっと読んできましたが、これはしっかりした本で（ただやや難しいです）、機械学習・ディープラーニングブームでひどいと正直ブームにイナゴして煽ってるだけの怪しい本が出る中、そこらへんの本とは一線を画するものです。この講義を受講したあとなら、この前半のScikit-learnの部分はほぼ「ああ、あれね」って感じですらすら読めると思います。自分もこの講義の演習問題をPythonに移植する際、組み込みでやる場合はほとんどScikit-learnを使いました。Scikit-learnはどの分類器、回帰に対してもfit→predictという共通のインターフェイスを持っているので、直感的でわかりやすいんですよね。

また、Andrew Ng先生が現在執筆している本で『Machine Learning Yearning』というのがあります。メーリングリストに登録するとドラフト版が送られて来て、自分も登録してみました。その和訳がQiitaにも上がっています¹（探せばすぐ出てくるので見つけてみてください）。何年後になるかはわかりませんが、おそらく日本でもそのうち出版されると思います（確証はないが需要は確実にある）。
こっちは数式がほぼない平易な本で、機械学習の入門書として想定されていますが、事前知識なしで読むのとこの講義を受講してから読むのだと、そこに散りばめられているエッセンスがどう重要なのか、理解の仕方が違うのではないかと思います。

---

1. GitHubには有志が立ち上げた非公式の中国語翻訳もあります。世界的に需要あるんですね。https://github.com/xiaqunfeng/machine-learning-yearning ↩