Coursera Machine LearningをPythonで実装 - [Week8]k-Means, 主成分分析（PCA）

今回から教師なし学習に入ります。クラスタリングのアルゴリズムとしてk-Means（k平均法）を、次元削減法として主成分分析（PCA）をやりました。（長いよ！）

k-Meansは機械学習でなくてもデータマイニングで、主成分分析は統計で既に知っているかもしれません。今回やることはどちらのいいとこを機械学習サイドから見ていく感じです。

k-Meansではそのものの実装と、応用例として画像の減色操作を行います。Pythonでのk-MeansそのものはScikit-learn等のライブラリに任せてしまえばよいのですが、応用例をふまえると、このようなライブラリのない他の言語でのソフトウェア開発で必要になるかもしれません。そのため、ここでも組み込みk-Meansのほかに、k-Meansの本質的なアルゴリズムを自分で実装します。画像の減色の部分は、ライブラリや自分で実装などk-Meansのアルゴリズムがあるものとして、ここでは組み込みのみで実装します。

主成分分析（PCA）も同様に、そのものの実装と、応用例として画像の次元削減を行います。応用例は組み込みのみで説明します。行列計算数回ですむ単純なアルゴリズムです。

コード： gistからダウンロードできます

1. k-Meansを自分で実装　https://gist.github.com/koshian2/5fbbf460257d02cec7f2e38c8ee360c1
2. k-Meansを組み込み　https://gist.github.com/koshian2/74715968c10b0cdaec2329b9cc0f0542
3. 主成分分析を自分で実装　https://gist.github.com/koshian2/977f29e3baafee89bf3423078f3cc555
4. 主成分分析を組み込み　https://gist.github.com/koshian2/790f0ab03e05116957ab02450d3c173d

##これまでの目次

• Coursera Machine LearningをPythonで実装 - [Week2]単回帰分析、重回帰分析
• Coursera Machine LearningをPythonで実装 - [Week3]ロジスティック回帰
• Coursera Machine LearningをPythonで実装 - [Week4]ニューラルネットワーク(1)
• Coursera Machine LearningをPythonで実装 - [Week5]ニューラルネットワーク(2)
• Coursera Machine LearningをPythonで実装 - [Week6]正則化、Bias vs Variance
• Coursera Machine LearningをPythonで実装 - [Week7]サポートベクターマシン（SVM）

##注意点まとめ
###k-Means

• k-Meansは凸最適化のような保証がないので、局所解にハマる可能性がある。初期の重心をランダムに変え何回かk-Meansを行い、その中から最も良いクラスタリングの結果を採用するのが良い。
• クラスタの数Kの選び方は難しい。縦軸にコスト関数の値J、横軸にKを取り、グラフが肘のようにカクっと曲がっているポイントを探すElbow法というのがあるが、なだらかに下がっていた場合は使えない。例えば、体重と身長を取り、Tシャツのサイズをクラスタリングするような例の場合は、K=3（S,M,L）とするのが良いか、K=5（XS,S,M,L,XL）とするのが良いかは、どちらが採算がとれるか（つまりプロジェクトのより高いレベルでの問題）が参考になるだろう、とのこと。

###主成分分析

• 必ず標準化すること
• 主成分分析をオーバーフィッティングの解消目的で使うべきではない→正則化すべき
• 最初から主成分分析による変数変換を使うべきではない。生データで一度試してみてうまくいかないことを確認してから使うべき。遅かったり、ハードウェア上の問題が出てきたらPCAをすべき。
• 多次元のデータを可視化するために主成分分析を使うのは有効

「主成分分析をオーバーフィッティングの解消目的で使ってはいけない。こういう使い方をしてほしくない」と先生に一蹴されたのは度肝を抜きました。主成分分析で多重共線性を解消するのはよいが、オーバーフィッティングを解消することは主眼ではないということなんでしょうね。ここごっちゃになりやすいので注意しないといけません¹。

##◎k-MeansをScikit-learnで実装
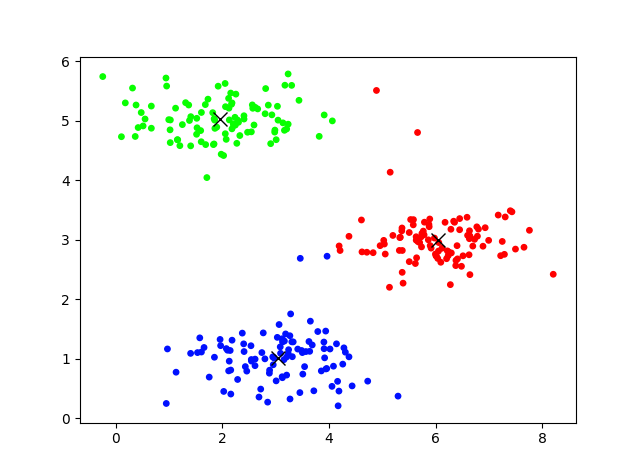
###1.2次元のクラスタリング
sklearn.cluster.KMeansを使います。クラスタリングのインスタンスを作成→fit→predictするなり、パラメーターを見るなりといういつもの方法です。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from scipy.io import loadmat

# data2の読み込み
X = np.array(loadmat("ex7data2.mat")['X'])
# K=3でクラスタリング
# initで初期値のとり方を選ぶ。デフォルトのk-means++（randomも選べる）
# n_initは異なる初期値で回す回数
clst = KMeans(n_clusters = 3, init="k-means++", n_init=10)
# fitで計算
clst.fit(X)
# cluster_centers_で重心の座標
print("cluster_centers_ : ")
print(clst.cluster_centers_)
print()
# labels_でどの重心かのインデックスを表示
print("labels_ (Take 10) : ")
print(clst.labels_[:10])
# 可視化
palette = np.linspace(0, 1, clst.n_clusters + 1)
color = palette[np.array(clst.labels_, dtype=int)]
plt.scatter(X[:, 0], X[:, 1], 15, c=plt.cm.hsv(color))
plt.plot(clst.cluster_centers_[:, 0], clst.cluster_centers_[:, 1], "x", color="k", markersize=10, linewidth=3)
plt.show()

重心の初期値の選び方の引数initのデフォルトは"k-means++"で、これは公式ドキュメントによると計算のスピードアップのために、賢く初期値を選ぶやり方とのことです。"random"も選択できます。n_initは異なる初期値を選んで繰り返す回数で、その中から最も良い結果を出力します。

出力

cluster_centers_ :
[[ 6.03366736  3.00052511]
 [ 1.95399466  5.02557006]
 [ 3.04367119  1.01541041]]

labels_ (Take 10) :
[1 0 0 1 1 1 1 1 1 1]

labelsの値は実行ごとに変わりますが、結果はだいたい同じです（同じクラスターが赤に分類されるか、緑に分類されるかの違いだけ）。

うまくいきましたね。

###2.k-Meansを用いた画像の減色処理
より実践的な例として、画像の減色処理をk-Meansで行うことができます。演習問題の画像より、この鳥の画像をいい感じに減色処理してみます。

これをbird_small.pngとして保存しておきます。難しそうですが結構簡単にできますよ。まず画像を読み込みます。PILパッケージを使うと簡単に読み込むことができます。

## 2.画像の減色
from PIL import Image
# 画像の読み込み
img = np.asarray(Image.open("bird_small.png")) #(128,128,3)のテンソル
img_array = img.reshape(img.shape[0]*img.shape[1], img.shape[2]) / 255 #(128*128, 3)の行列に変形

横×縦×深さの画素値のテンソルとして読み込まれます。32ビット画像の場合はRGBの他に透明度が加わるかもしれません。扱いやすいように行列に変換します。imshowの表示を上手くために255で割ります（割らないとプロットがバグる）。

k-meansでサクッと減色させます。n_clustersの数＝減色数となります。

# k-meansで減色
# n_clusters:減色数
clst = KMeans(n_clusters=16)
label = clst.fit_predict(img_array)

画像として戻す場合も難しいことはありません。クラスターの重心の座標にラベルのベクトルを入れてあげればいいです（Numpyの行列変形なのでむちゃくちゃ速いです）。

# 画像として復元
img_array_quant = clst.cluster_centers_[label] #(128*128, 3)の行列
img_quant = img_array_quant.reshape(img.shape)

あとはプロットします。

# プロットに表示(imshowで上手く表示するために[0,1]のfloatにしておくこと)
fig = plt.figure()
ax = fig.add_subplot(1, 2, 1, xticks=[], yticks=[])
ax.imshow(img)
ax.set_title("Original")
ax = fig.add_subplot(1, 2, 2, xticks=[], yticks=[])
ax.imshow(img_quant)
ax.set_title("k-Means Color Quantization (K = 16)")
plt.show()

この通り。とてもいい感じになりました。なぜいい感じに色が選ばれたのかというと、まさにクラスタリングしたからです。やっていることはRGB、3次元の変数（feature）に対してクラスタリングをしただけです。クラスターの重心の画素値が選ばれた色となります。

なかなか使い所の多そうなアルゴリズムだと思います。

##◎主成分分析をScikit-learnで実装
主成分分析もScikit-learnでできます。ただし、組み込みを使う場合でも標準化は忘れないようにしましょう。これは公式ドキュメントにも書いてあります。

参考：Importance of Feature Scaling

この公式ドキュメントを要約すると、標準化して主成分分析したデータと、標準化せずに主成分分析したデータを、それぞれガウスの単純ベイズ分類器にかけテストデータに対する精度を比較すると、標準化したほうは98.15%を出したのに対し、標準化しなかったほうは81.48%しか出ない――という内容です。つまり、主成分分析段階での標準化の有無は、その後の分析の精度に直結します。

###1.2次元のデータの主成分分析
まずは2次元のデータを1次元に圧縮します。扱っているデータは後述の「自分で実装」のところにあるものと同じです。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from scipy.io import loadmat
from sklearn.preprocessing import StandardScaler


## 1.2次元の主成分分析
#データの読み込み（自分で実装するケースでハードコーディングしたものと同じ）
X = np.array(loadmat("ex7data1.mat")['X'])
# 標準化
# 参考：http://scikit-learn.org/stable/auto_examples/preprocessing/plot_scaling_importance.html
scaler = StandardScaler()
X_norm = scaler.fit_transform(X)
# PCA（標準化を事前に行うこと）
pca = PCA(n_components=1, svd_solver="full")
X_project = pca.fit_transform(X_norm)
X_recover = pca.inverse_transform(X_project)
# 元データ
print("Original fist sample:", X_norm[0, :])
# PCAで次元削減
print("Projection of the first example:", X_project[0])
# 削減したデータの次元を戻す
print("Approximation of the first example:", X_recover[0,:])
# 説明される分散比（n_componentsはこれで調整する、次元削減しない[=N]なら1）
print("Explained variance ratio:", pca.explained_variance_ratio_)
print()

標準化も主成分分析もfit_transform()で一発。主成分分析のPCAではn_componentsで削減する次元数を指定できます。次元を削減したのち、inverse_transform()で変換済みのデータを代入すると、次元の復元ができます（当然非可逆圧縮です）。

出力

Original fist sample: [-0.52331306 -1.59279252]
Projection of the first example: [ 1.49631261]
Approximation of the first example: [-1.05805279 -1.05805279]
Explained variance ratio: [ 0.86776519]

主成分分析のexplained_variance_ratio_はどの程度分散を保っているか、平たく言えばどの程度変換前の情報を持っているか、を示すパラメーターです。元のデータの分散と完全に同じなら1、元のデータの分散が完全に潰れてしまったら0となります。

したがって、どこまで次元を削ればいいか（n_componentsの設定値）は、explained_variance_ratio_を見ましょう。今n_componentsの設定値が1なので1次元のベクトルですが、設定値を増やすとその数に見合った固有ベクトルに対応する、次元のベクトルがexplained_variance_ratio_に渡されます。n_components=の設定値を元データの次元数とすれば、その和は1となります（全く情報が失われていないので）。

例えば、**元の分散を99%残したいというときは、explained_variance_ratio_の累積和を取り、0.99を超えた所の次元＝n_components**とすればよいのです。explained_variance_ratio_そのものは逓減していくはずなので、そのものの値ではなく累積和を取ることがポイントです。

###2.顔画像の次元削減
より実践的な例として、顔画像（5000×1024の行列）の次元削減をしてみます。まずデータを読み込みます。

## 2.顔画像
X = np.array(loadmat("ex7faces.mat")['X'])
# プロットしてみる
def display_data(X, example_width = np.sqrt(X.shape[1]).astype(int)):
    m, n = X.shape
    display_rows = np.floor(np.sqrt(m)).astype(int)
    display_cols = np.ceil(m / display_rows).astype(int)

    fig = plt.figure(figsize=(5,5))
    fig.subplots_adjust(hspace=0.05, wspace=0.05)
    for i in range(X.shape[0]):
        ax = fig.add_subplot(display_rows, display_cols, i+1, xticks=[], yticks=[])
        ax.imshow(X[i, :].reshape(example_width, example_width, order="F"), cmap="gray")

# 元は1024次元
display_data(X[:100, :])
plt.suptitle("Original faces")
plt.show()

標準化して、主成分分析をかけます。ここでは1024次元から100次元に圧縮します。

# 標準化する
scaler = StandardScaler()
X_norm = scaler.fit_transform(X)
# 主成分分析で100次元にする
pca = PCA(n_components=100)
Z = pca.fit_transform(X_norm)
print("Faces data : PCA 1024dim -> 100dim, Explained varience ratio:", np.sum(pca.explained_variance_ratio_))

ちなみに分散は93%残っているそうです。

出力

Faces data : PCA 1024dim -> 100dim, Explained varience ratio: 0.931897155391

固有値ベクトルを最初の36個出力します。

# 固有ベクトルの最初の36個をプロット
display_data(pca.components_[:36, :])
plt.suptitle("Eigen vectors")
plt.show()

輪郭そのものが抽出できて「おっ！？」となりますが、下のほうにいくほど、だんだん似たような輪郭になっているのがわかります。これはexplained_variance_ratio_と関係しており、この値が下に行くほど少なくなってくる（平たく言えば持っている固有の情報が逓減してくる）からです。画像処理における固有ベクトルってこういう意味があったんですね。ちなみに組み込みのPCAでの固有ベクトルはcomponents_で見れます。

100次元に圧縮したデータを元の1024次元に復元すると次のようになります。

# 復元する
X_rec = pca.inverse_transform(Z)
display_data(X_rec[:100,])
plt.suptitle("Recovered faces")
plt.show()

元の画像と見比べてみると、分散比93%でも結構情報が落ちているように見えます。人ごとの固有の表情というか目や口元の輪郭がぼやけている印象を受けます。93%というと結構高い数値に見えますが、キーになる情報はすぐ落ちてしまうので、先生の言う「主成分分析よりもまず生のデータで試してみなさい」というのも確かにそうだなという実感できました。

##・k-Meansを自分で実装
k-Meansに戻ります。とても単純なアルゴリズムなのでぜひ自分で実装してみましょう。
###1.最も近い重心を探す

import numpy as np
import matplotlib.pyplot as plt
import copy

# データ2の読み込み
X = np.array([[1.84208,4.60757],[5.65858,4.79996],[6.35258,3.29085],[2.90402,4.61220],[3.23198,4.93989],[1.24792,4.93268],[1.97620,4.43490],[2.23454,5.05547],[2.98341,4.84046],[2.97970,4.80671],[2.11496,5.37374],[2.12170,5.20854],[1.51435,4.77003],[2.16979,5.27435],[0.41852,4.88313],[2.47054,4.80419],[4.06069,4.99504],[3.00709,4.67898],[0.66632,4.87188],[3.16219,4.83658],[0.51155,4.91053],[3.13428,4.96178],[2.04975,5.62414],[0.66583,5.24399],[1.01732,4.84474],[2.17894,5.29759],[2.85963,5.26042],[1.30883,5.30159],[0.99253,5.01567],[1.40373,4.57528],[2.66047,5.19624],[2.79996,5.11526],[2.06995,4.68467],[3.29765,5.59206],[1.89298,4.89043],[2.55983,5.26398],[1.15354,4.67867],[2.25151,5.44500],[2.20960,4.91469],[1.59142,4.83213],[1.67838,5.26904],[2.59149,4.92593],[2.80996,5.53850],[0.95312,5.58037],[1.51775,5.03837],[3.23114,5.78430],[2.54180,4.81099],[3.81423,4.73527],[1.68496,4.59644],[2.17777,4.86154],[1.81733,5.13334],[1.85777,4.86962],[3.03084,5.24058],[2.92658,5.09668],[3.43494,5.34081],[3.20367,4.85925],[0.10512,4.72916],[1.40598,5.06637],[2.24185,4.92446],[1.36678,5.26161],[1.70725,4.04231],[1.91910,5.57848],[1.60157,4.64453],[0.37963,5.26195],[2.02135,4.41267],[1.12037,5.20881],[2.26901,4.61819],[-0.24513,5.74019],[2.12858,5.01150],[1.84420,5.03154],[2.32558,4.74868],[1.52334,4.87916],[1.02285,5.01051],[1.85383,5.00752],[2.20322,4.94516],[1.20100,4.57830],[1.02063,4.62991],[1.60493,5.13663],[0.47647,5.13536],[0.36392,4.73333],[0.31320,5.54695],[2.28665,5.00767],[2.15460,5.46283],[2.05289,4.77959],[4.88804,5.50671],[2.40305,5.08147],[2.56869,5.20688],[1.82976,4.59657],[0.54845,5.02673],[3.17110,5.59465],[3.04202,5.00758],[2.40428,5.02587],[0.17783,5.29765],[2.61429,5.22287],[2.30098,4.97236],[3.90779,5.09465],[2.05671,5.23391],[1.38133,5.00195],[1.16074,4.67728],[1.72818,5.36028],[3.20361,0.72221],[3.06193,1.57192],[4.01715,1.16071],[1.40261,1.08727],[4.08165,0.87200],[3.15273,0.98156],[3.45186,0.42784],[3.85384,0.79205],[1.57449,1.34811],[4.72372,0.62044],[2.87961,0.75414],[0.96791,1.16167],[1.53178,1.10055],[4.13836,1.24781],[3.16109,1.29423],[2.95177,0.89583],[3.27844,1.75044],[2.12702,0.95672],[3.32649,1.28019],[2.54371,0.95733],[3.23395,1.08202],[4.43153,0.54041],[3.56479,1.11765],[4.25588,0.90644],[4.05387,0.53292],[3.08970,1.08814],[2.84734,0.26759],[3.63586,1.12160],[1.95539,1.32157],[2.88384,0.80455],[3.48444,1.13551],[3.49798,1.10046],[2.45576,0.78905],[3.20380,1.02728],[3.00677,0.62519],[1.96548,1.21731],[2.17989,1.30880],[2.61207,0.99077],[3.95550,0.83269],[3.64846,1.62850],[4.18450,0.45356],[3.78757,1.45443],[3.30064,1.28108],[3.02836,1.35635],[3.18412,1.41411],[4.16912,0.20581],[3.24024,1.14876],[3.91596,1.01226],[2.96980,1.01210],[1.12994,0.77085],[2.71731,0.48698],[3.11890,0.69438],[2.40518,1.11778],[2.95818,1.01887],[1.65456,1.18631],[2.39776,1.24721],[2.28409,0.64865],[2.79589,0.99527],[3.41156,1.15964],[3.50664,0.73878],[3.93616,1.46203],[3.90207,1.27779],[2.61036,0.88028],[4.37272,1.02914],[3.08349,1.19633],[2.11599,0.79304],[2.15653,0.40359],[2.14491,1.13582],[1.84936,1.02233],[4.15908,0.61721],[2.76494,1.43149],[3.90561,1.16575],[2.54072,0.98393],[4.27783,1.18014],[3.31058,1.03124],[2.15521,0.80697],[3.71364,0.45813],[3.54010,0.86446],[1.60520,1.10981],[1.75164,0.68854],[3.12405,0.67822],[2.37199,1.42790],[2.53446,1.21562],[3.68345,1.22835],[3.26701,0.32057],[3.94159,0.82577],[3.26455,1.38369],[4.30471,1.10726],[2.68499,0.35345],[3.12635,1.28069],[2.94294,1.02825],[3.11877,1.33285],[2.02359,0.44772],[3.62203,1.28644],[2.42866,0.86499],[2.09517,1.14010],[5.29239,0.36873],[2.07292,1.16764],[0.94623,0.24522],[2.73912,1.10072],[6.00507,2.72784],[6.05696,2.94970],[6.77013,3.21411],[5.64035,2.69385],[5.63325,2.99002],[6.17443,3.29026],[7.24695,2.96877],[5.58163,3.33510],[5.36272,3.14681],[4.70776,2.78711],[7.42892,3.46679],[6.64107,3.05999],[6.37474,2.56253],[7.28780,2.75180],[6.20295,2.67856],[5.38736,2.26737],[5.66731,2.96478],[6.59702,3.07082],[7.75661,3.15604],[6.63263,3.14799],[5.76635,3.14272],[5.99423,2.75708],[6.37870,2.65022],[5.74036,3.10391],[4.61652,2.79321],[5.33534,3.03929],[5.37294,2.81685],[5.03611,2.92486],[5.52909,3.33682],[6.05087,2.80703],[5.13201,2.19812],[5.73285,2.87738],[6.78111,3.05677],[6.44834,3.35299],[6.39941,2.89757],[5.86068,2.99577],[6.44765,3.16561],[5.36708,3.19503],[5.88736,3.34616],[3.96162,2.72025],[6.28438,3.17361],[4.20585,2.81647],[5.32616,3.03314],[7.17135,3.41227],[7.49493,2.84019],[7.39807,3.48487],[5.02433,2.98683],[5.31712,2.81741],[5.87655,3.21661],[6.03763,2.68304],[5.91280,2.85632],[6.69451,2.89056],[6.01018,2.72401],[6.92722,3.19960],[6.33560,3.30864],[6.24257,2.79179],[5.57812,3.24766],[6.40774,2.67555],[6.80030,3.17580],[7.21684,2.72897],[6.51101,2.72732],[4.60631,3.32946],[7.65503,2.87096],[5.50296,2.62925],[6.63061,3.01502],[3.45928,2.68478],[8.20340,2.41693],[4.95679,2.89776],[5.37053,2.44955],[5.69798,2.94977],[6.27376,2.24256],[5.05275,2.75692],[6.88576,2.88845],[4.18774,2.89283],[5.97510,3.02592],[6.09457,2.61868],[5.72396,3.04454],[4.37250,3.05488],[6.29206,2.77574],[5.14533,4.13226],[6.58706,3.37508],[5.78769,3.29255],[6.72798,3.00440],[6.64079,2.41069],[6.23229,2.72851],[6.21773,2.80995],[5.78116,3.07988],[6.62447,2.74454],[5.19591,3.06973],[5.87177,3.25518],[5.89562,2.89844],[5.61754,2.59751],[5.63176,3.04759],[5.50259,3.11869],[6.48213,2.55085],[7.30279,3.38016],[6.99198,2.98707],[4.82553,2.77962],[6.11768,2.85476],[0.94049,5.71557]])

## 1.最も近い重心を探す
# 最も近い重心も求める関数
def find_closest_centroids(X, centroids):
    idx = np.zeros(X.shape[0])
    K = centroids.shape[0]
    for i in range(X.shape[0]):
        distances = np.zeros(K)
        for j in range(K):
            distances[j] = np.linalg.norm(X[i, :] - centroids[j, :]) ** 2
        idx[i] = np.argmin(distances)
    return idx

# 初期値
K = 3
initial_centroids = np.array([[3,3],[6,2],[8,5]])
# 重心の初期値を用いて最も近い重心を求める
idx = find_closest_centroids(X, initial_centroids)
print("Closest centroids for the first 3 examples:")
print(" ", idx[:3])
print("(the closest centroids should be 0, 2, 1 respectively)\n")

データを読み込み、最も近い重心を求めるアルゴリズム部分です。centroidsには仮においた重心が入り、XがM×Nの行列であったときに（Mはデータ数、Nはデータの次元数）、centroidsはK×Nの行列になります。for文を使わない実装もあるはずですがどうやるかわからなかったので、forで脳死しました。他言語ならこれで大丈夫です。

出力

Closest centroids for the first 3 examples:
  [ 0.  2.  1.]
(the closest centroids should be 0, 2, 1 respectively)

ここでは各データの点に対する、最も近い重心のインデックスが返されます。

2.平均を計算

次に、仮にラベル付けされた重心別に、それらの座標の平均を計算します。重心とは座標の平均なので、ここで計算された値が新しい重心となります。これを繰り返していくのがk-Meansなのです（アルゴリズムはシンプルながら強力！）。

python

## 2.平均を計算
def compute_centroids(X, idx, K):
    m, n = X.shape
    centroids = np.zeros((K, n))
    for i in range(K):
        filter = idx == i
        if filter.any():
            centroids[i, :] = np.mean(X[filter, :], axis=0)
    return centroids
# 重心の平均を計算
centroids = compute_centroids(X, idx, K)
print("Centroids computed after initial finding of closest centroids:")
print(centroids)
print("(the centroids should be")
print("   [ 2.428301 3.157924 ]")
print("   [ 5.813503 2.633656 ]")
print("   [ 7.119387 3.616684 ]\n")

ここで出てきた値は初期に与えた重心をもとに、次の重心を計算したものです。本来この初期値はランダムにサンプルを抽出して与えます。

出力

Centroids computed after initial finding of closest centroids:
[[ 2.42830089  3.15792429]
 [ 5.8135032   2.63365641]
 [ 7.11938667  3.61668167]]
(the centroids should be
   [ 2.428301 3.157924 ]
   [ 5.813503 2.633656 ]
   [ 7.119387 3.616684 ]

###3.k-Meansクラスタリング
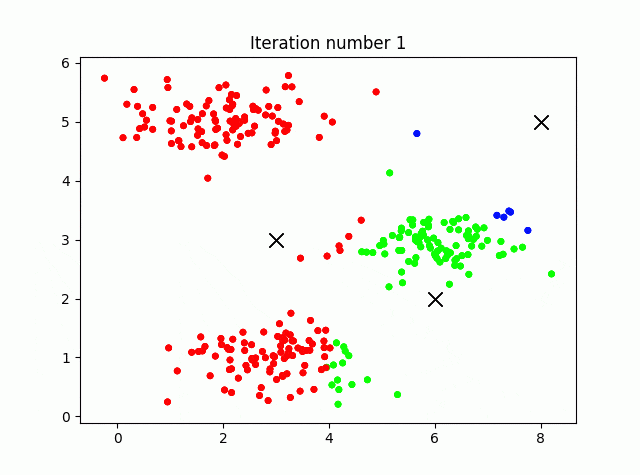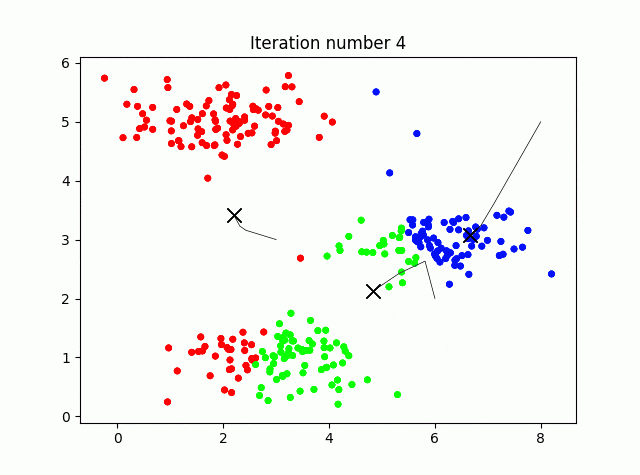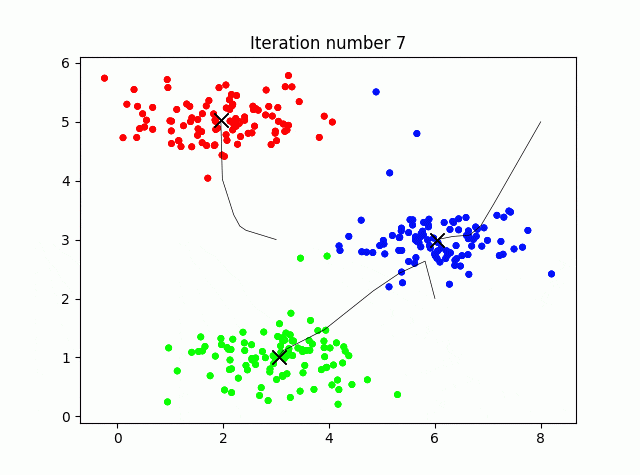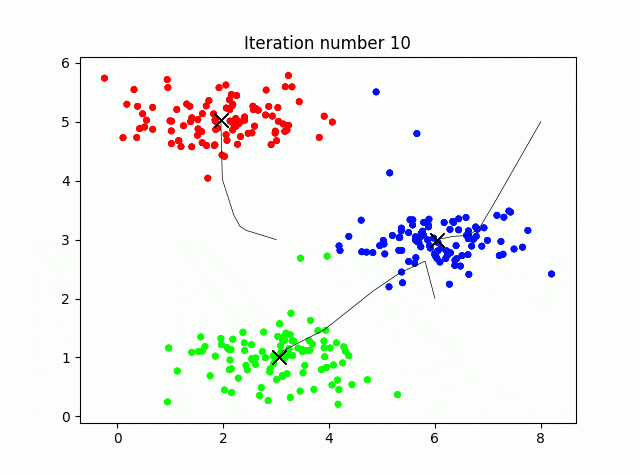
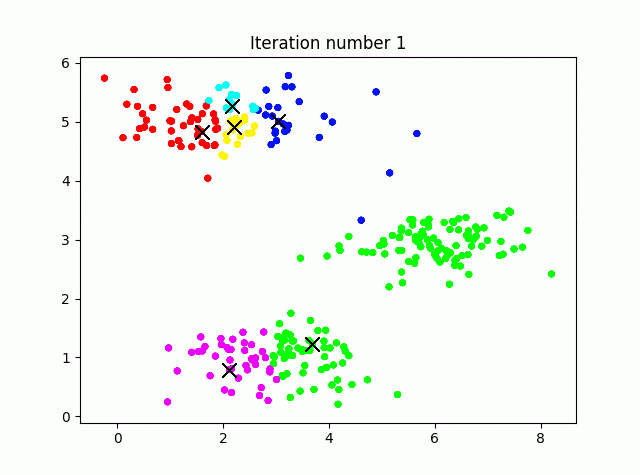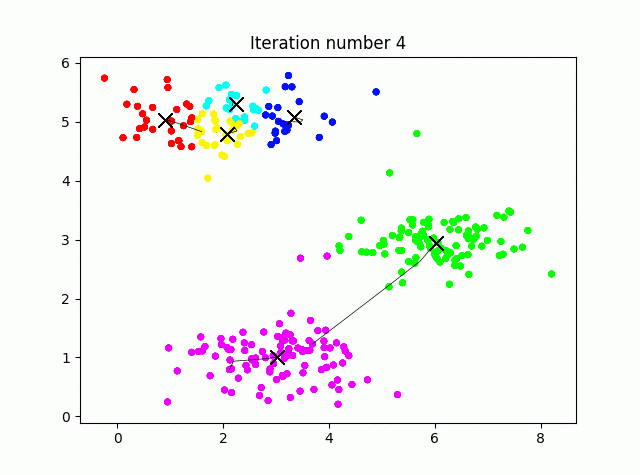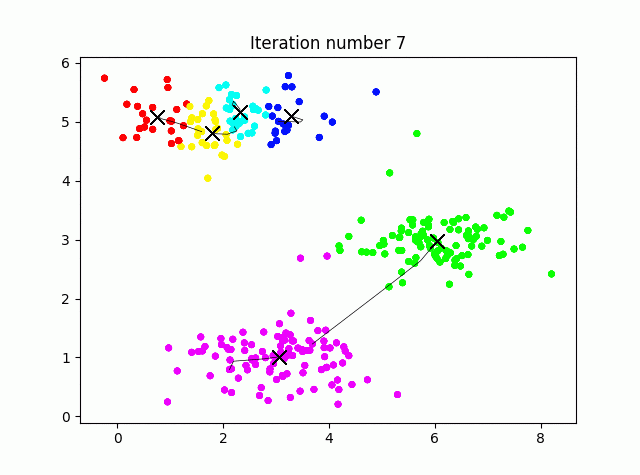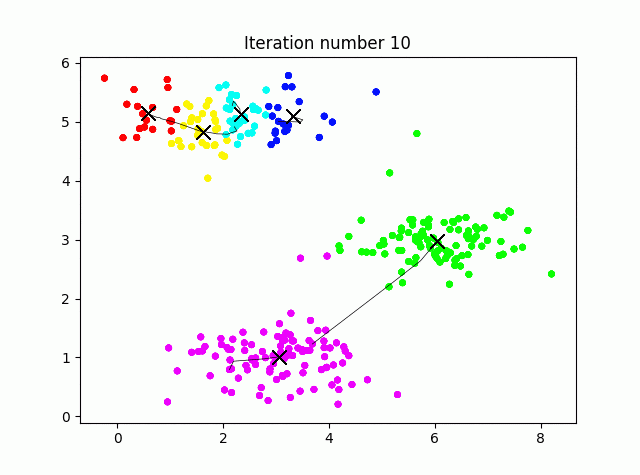
クラスタリングの工程を可視化しながら実行してみます。コード長めですが、ほぼ可視化のためのものです。

## 3.K-meansクラスタリング
max_iters = 10
def plot_data_points(X, idx, K):
    palette = np.linspace(0, 1, K+1)
    color = palette[np.array(idx, dtype=int)]
    plt.scatter(X[:, 0], X[:, 1], 15, c=plt.cm.hsv(color))

def plot_progress_kmeans(X, centroids, previous, idx, K, i):
    for j in range(centroids.shape[0]):
        plt.plot(centroids[:, 0], centroids[:, 1], "x", color="k", markersize=10, linewidth=3)
        plot_data_points(X, idx, K)
        plt.plot(previous[:(i+1), j, 0], previous[:(i+1), j, 1], linewidth=0.5, color="k")
    plt.title(f"Iteration number {i+1}")

def run_kmeans(X, initial_centroids, max_iters, plot_progress=True):
    m, n = X.shape
    K = initial_centroids.shape[0]
    centroids = initial_centroids
    previous_centroids = np.zeros((max_iters, K, n))

    for i in range(max_iters):
        print(f"K-means iteration {i+1} / {max_iters}")
        idx = find_closest_centroids(X, centroids)
        previous_centroids[i, :, :] = centroids
        # オプションで進行をプロットする
        if plot_progress:
            plot_progress_kmeans(X, centroids, previous_centroids, idx, K, i)
            plt.show()
        # 新しい重心を計算
        centroids = compute_centroids(X, idx, K)
    return centroids, idx

# k-Meansを実行
centroids, idx = run_kmeans(X, initial_centroids, max_iters, True)
print("k-Means Done.\n")

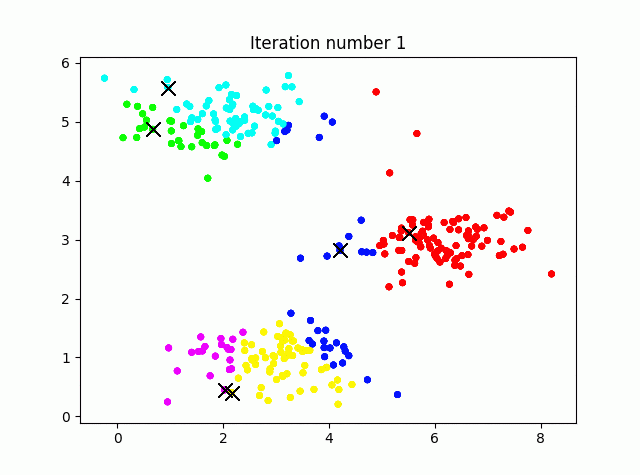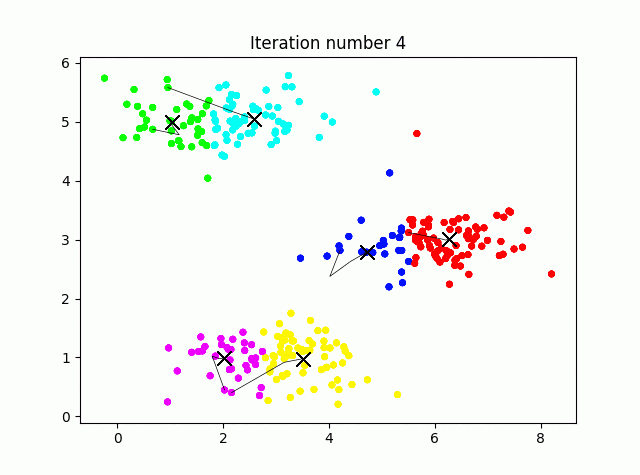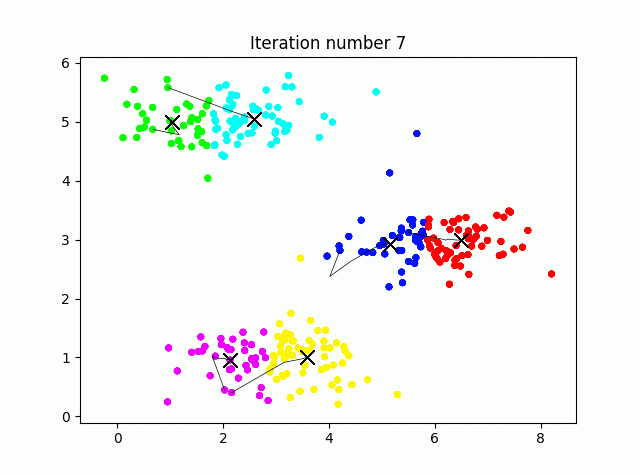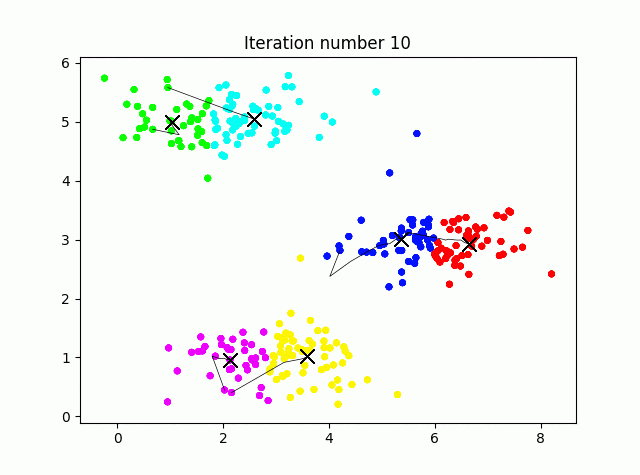
###4.初期値をランダム化
本来k-Meansの初期の重心はランダムに与えるべきです。K=3ではどれも似たような結果に収束しますが、例えばK=6としてやると、初期値ごとに別の結果を示すことがわかります（つまりデータに依存します）。

## 4.初期値をランダム化
def kmeans_init_centroids(X, K, seed):
    randidx = np.arange(X.shape[0])
    np.random.seed(seed)
    np.random.shuffle(randidx)
    centroids = X[randidx[:K], :]
    return centroids

K = 6
seed = 4 #ここをいろいろ変えてみる
initial_centroids = kmeans_init_centroids(X, K, seed)
centroids, idx = run_kmeans(X, initial_centroids, max_iters, True)
print("k-Means Done.\n")

K=6で固定して、ランダムのシードを4と9でやってみました。上がseed(4)、seed(9)の例です。

このように結果が初期値に依存します。なんだか国盗りゲームみたいで面白いですね。ちなみにどのクラスタリング（結果）を選ぶかは、データの各点とそれぞれが割り当てられた点とのユークリッド距離の2乗和を最小化するようなクラスタリングを選びます。コスト関数はコードで書くと次のようになります。

# コスト関数
def costfunction(X, centroids, idx):
    m = X.shape[0]
    J = 0
    for i in range(m):
        J += np.linalg.norm(X[i, :] - centroids[int(idx[i]), :]) ** 2 / m
    return J
J = costfunction(X, centroids, idx)
print(f"Cost function (where seed = {seed}) : {J}")

seed=4, 9の場合でコスト関数の値を計算すると次のようになります。

出力

Cost function (where seed = 4) : 0.40403657634436035
Cost function (where seed = 9) : 0.6236206021728188

つまり、seed=4のときのクラスタリングは、seed=9のときよりも相対的に良いということになります。これはプロットした図を見れば一目瞭然ですね。

##・主成分分析を自分で実装
特異値分解するだけなので単純です。自分で実装する場合もデータの標準化を必ずすることを忘れないようにしましょう。これは主成分分析の理論上必要なものです。

###1.データの読み込み

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler

##1.データの読み込み
# データの読み込み
X = np.array([[3.3816,3.3891],[4.5279,5.8542],[2.6557,4.4120],[2.7652,3.7154],[2.8466,4.1755],[3.8907,6.4884],[3.4758,3.6328],[5.9113,6.6808],[3.9289,5.0984],[4.5618,5.6233],[4.5741,5.3977],[4.3717,5.4612],[4.1917,4.9547],[5.2441,4.6615],[2.8358,3.7680],[5.6353,6.3121],[4.6863,5.6652],[2.8505,4.6265],[5.1102,7.3632],[5.1826,4.6465],[5.7073,6.6810],[3.5797,4.8028],[5.6394,6.1204],[4.2635,4.6894],[2.5365,3.8845],[3.2238,4.9426],[4.9295,5.9550],[5.7930,5.1084],[2.8168,4.8190],[3.8888,5.1004],[3.3432,5.8930],[5.8797,5.5214],[3.1039,3.8571],[5.3315,4.6807],[3.3754,4.5654],[4.7767,6.2544],[2.6757,3.7310],[5.5003,5.6795],[1.7971,3.2475],[4.3225,5.1111],[4.4210,6.0256],[3.1793,4.4369],[3.0335,3.9788],[4.6093,5.8798],[2.9638,3.3002],[3.9718,5.4077],[1.1802,2.8787],[1.9190,5.0711],[3.9552,4.5053],[5.1180,6.0851]])

###2.主成分分析
特異値分解して固有ベクトルを確認しているだけです。

##2.主成分分析
# データの標準化
# 自分で実装する場合は事前に必ず標準化する
scaler = StandardScaler()
X_norm = scaler.fit_transform(X)
# 主成分分析の関数
def pca(X):
    m = X.shape[0]
    sigma = np.dot(X.T, X) / m
    U, S, V = np.linalg.svd(sigma) #特異値分解
    return U, S
U, S = pca(X_norm)
# 固有ベクトルのチェック
print("Top eigenvector: ")
print(" U[:,0] =", U[0, 0], U[1, 0])
print("(you should expect to see -0.707107 -0.707107)")
print()

出力

Top eigenvector:
 U[:,0] = -0.707106781187 -0.707106781187
(you should expect to see -0.707107 -0.707107)

###3.次元の削減→復元
OctaveとPythonで出てくる値に若干誤差があります。

##3.次元の削減
# 次元の削減
def project_data(X, U, K):
    Ureduce = U[:, :K]
    Z = np.dot(X, Ureduce)
    return Z
# 次元の復元
def recover_data(Z, U, K):
    Uredece = U[:, :K]
    X_rec = np.dot(Z, Uredece.T)
    return X_rec
print("Dimension reduction on example dataset.")
print("Before projection : ", X_norm[0,:])
K = 1
Z = project_data(X_norm, U, K)
print("Projection of the first example:", Z[0])
print("(this value should be about 1.481274)")
X_rec = recover_data(Z, U, K)
print("Approximation of the first example:", X_rec[0,:])
print("(this value should be about  -1.047419 -1.047419)")

主成分分析で一度次元を落としてしまうと、やはり完璧には戻りません。それはそうです。Uの次元を制限した時点で不可逆な圧縮になってしまいますから。ただ全ての変数が独立ではなく、変数間に従属性があるならこの手法は有効でしょう。

出力

Dimension reduction on example dataset.
Before projection :  [-0.52327626 -1.59279926]
Projection of the first example: [ 1.49629135]
(this value should be about 1.481274)
Approximation of the first example: [-1.05803776 -1.05803776]
(this value should be about  -1.047419 -1.047419)

以上です。結構長くなってしまいましたね。

1. 半分愚痴ですが、多重共線性とオーバーフィッティングって重回帰分析の問題点のように同時に語られることが多くて混同しやすい（ネットで見ていると混同しているケースもあります）。オーバーフィッティングとは「訓練データを最適化して解いたパラメーターを代入したときに、交差検証に対する誤差と、訓練データに対する誤差との間に大きなギャップがある状態。特に、訓練データに対する誤差は小さいが、交差検証データに対する誤差は大きい状態」と（ありがちな統計の本では）明瞭に定義しないのが良くないんじゃないかなと思います。 ↩