CNNを使って「同じ構造の」ニューラルネットワーク同士のアンサンブル学習の効果を確認します。そんなの意味ないんじゃないか?と思われるかもしれませんが、実はありました。End-to-Endなアンサンブル学習ができます。
アンサンブル学習とは
複数の弱分類器を使ってより高い精度の分類器をつくること。わかりやすく言えばこれ↓
http://evangelion.wikia.com/wiki/Magi より
エヴァのMAGIシステムで1つのコンピューターを1つの分類器とみなせば、その分類器が出した答えの多数決を取ることは、立派な「アンサンブル学習」です。もちろん自爆決議のように全員が一致しないとダメという設定もできると思います1。
意味のあるアンサンブル学習、意味のないアンサンブル学習
いくら多数決といえど、分類器が全く同じもので多数決をとってもそんなの意味ありません。MAGIシステムの自爆決議でカスパーが裏切ったのは、それぞれのコンピューターに赤木ナオコ博士の「科学者、母親、女」という別々の人格を移植したからで、もし同一の人格をしてたらこのようなことは多分起こらなかったのではないかと思います。
さて、アンサンブルの効果を定量的に判断する指標として、分類器同士の「(ピアソンの)相関係数」を見るという方法があります。Kaggleに投稿されていた記事の和訳からです。
次の場合、ブレンディングによるメリットはありません。
モデルのピアソンの相関係数が0.99を超えている
かつ、コルモゴロフ–スミルノフ検定の結果が0.01を下回逆に、以下の場合はブレンディングによるメリットがあります。
逆にピアソンが0.95以下
かつ、スミルノフ検定が0.05よりも大きい。
コルモゴロフ–スミルノフ検定はおいておくとして、今相関係数だけ見るものとしましょう。例えば、「犬(=0)or猫(=1)」という二値分類を考えたときに、分類器Aが「1, 1, 0, 0」、分類器Bが「1, 1, 0, 0」と全く同じ答えを出した場合は、相関係数は1となります。この場合のアンサンブルは全く意味がありません。
相関係数は-1~1の間で定義されるので、「だいたいは合ってるんだけど微妙に違う分類器同士を組み合わせなさいよ」というのが相関係数0.95以下をブレンディングしろという主張の意味することです。確かに相関係数を指標とするのはわかりやすいです。
End-to-Endなアンサンブル学習
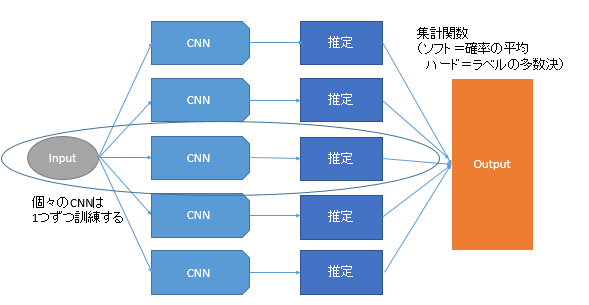
これはディープラーニングの強みでもあるのですが、個々の分類器の学習から全体の集計までを1つの流れで、つまり「End-to-End」なアプローチですることもできます。今回の記事の大きな特徴です。
今回は分類器は5個としました。集計関数に多数決を使う場合は、分類器は奇数のほうがいいです。個々の分類器は普通の分類問題として訓練します。そのあと集計関数をかけて、全体の出力を計算します。
集計関数は今回2種類用意しました。
-
ソフトなアンサンブル : ラベルの推定確率どうしの平均を取る。例えば、分類器Aが犬=0.8・猫=0.2、分類器Bが犬=0.9、猫=0.1、分類器Cが犬=0.4、猫=0.6だったら、全体の出力は犬=0.7、猫=0.3となり、全体の出力は「犬」
となる。 - ハードなアンサンブル : 分類器単位でラベルを求め、その多数決を取る。同一の場合は、ラベルの番号が若いものを優先する2。例えば、ソフトな例なら、分類器Aは犬、分類器Bも犬、分類器Cは猫なので、全体の出力は多数決により「犬」となる。
コード
アンサンブルありの場合のコードは以下のとおりです。ネットワークは10層のVGGライクなCNNを使い、CIFAR-10で検証しました。
import tensorflow as tf
from tensorflow.keras.layers import Input, Conv2D, BatchNormalization, Activation, AveragePooling2D, GlobalAvgPool2D, Dense
from tensorflow.keras.models import Model
import tensorflow.keras.backend as K
from tensorflow.keras.callbacks import History, Callback
from tensorflow.contrib.tpu.python.tpu import keras_support
from keras.objectives import categorical_crossentropy
import numpy as np
from sklearn.metrics import confusion_matrix, accuracy_score
from keras.datasets import cifar10
from keras.utils import to_categorical
from scipy.stats import mode
import os, pickle
def basic_conv_block(input, chs, reps):
x = input
for i in range(reps):
x =Conv2D(chs, 3, padding="same")(x)
x = BatchNormalization()(x)
x = Activation("relu")(x)
return x
def create_cnn():
input = Input(shape=(32,32,3))
x = basic_conv_block(input, 64, 3)
x = AveragePooling2D(2)(x)
x = basic_conv_block(x, 128, 3)
x = AveragePooling2D(2)(x)
x = basic_conv_block(x, 256, 3)
x = GlobalAvgPool2D()(x)
x = Dense(10, activation="softmax")(x)
model = Model(input, x)
return model
# 確率の平均を取るアンサンブル(ソフトアンサンブル)
def ensembling_soft(models, X):
preds_sum = None
for model in models:
if preds_sum is None:
preds_sum = model.predict(X)
else:
preds_sum += model.predict(X)
probs = preds_sum / len(models)
return np.argmax(probs, axis=-1)
# 多数決のアンサンブル(ハードアンサンブル)
def ensembling_hard(models, X):
pred_labels = np.zeros((X.shape[0], len(models)))
for i, model in enumerate(models):
pred_labels[:, i] = np.argmax(model.predict(X), axis=-1)
return np.ravel(mode(pred_labels, axis=-1)[0])
class Checkpoint(Callback):
def __init__(self, model, filepath):
self.model = model
self.filepath = filepath
self.best_val_acc = 0.0
def on_epoch_end(self, epoch, logs):
if self.best_val_acc < logs["val_acc"]:
self.model.save_weights(self.filepath, save_format="h5")
self.best_val_acc = logs["val_acc"]
print("Weights saved.", self.best_val_acc)
def train(ensemble_type):
assert ensemble_type in ["hard", "soft"]
(X_train, y_train), (X_test, y_test) = cifar10.load_data()
X_train, X_test = X_train / 255.0, X_test / 255.0
y_test_label = np.ravel(y_test)
y_train, y_test = to_categorical(y_train), to_categorical(y_test)
n_estimators = 5
batch_size = 1024
models = []
global_hist = {"hists":[], "ensemble_test":[]}
single_preds = np.zeros((X_test.shape[0], n_estimators))
for i in range(n_estimators):
print("Estimator",i+1,"train starts")
train_model = create_cnn()
train_model.compile(tf.train.AdamOptimizer(), loss="categorical_crossentropy", metrics=["acc"])
tpu_grpc_url = "grpc://"+os.environ["COLAB_TPU_ADDR"]
tpu_cluster_resolver = tf.contrib.cluster_resolver.TPUClusterResolver(tpu_grpc_url)
strategy = keras_support.TPUDistributionStrategy(tpu_cluster_resolver)
train_model = tf.contrib.tpu.keras_to_tpu_model(train_model, strategy=strategy)
models.append(train_model)
hist = History()
cp = Checkpoint(train_model, f"weights_{i}.hdf5")
train_model.fit(X_train, y_train, batch_size=batch_size, callbacks=[hist, cp],
validation_data=(X_test, y_test), epochs=100)
# 最良のモデルの読み込み
train_model.load_weights(f"weights_{i}.hdf5")
for layer in train_model.layers:
layer.trainable = False
# 単体の推論
single_preds[:, i] = np.argmax(train_model.predict(X_test), axis=-1)
# アンサンブルの精度の記録
global_hist["hists"].append(hist.history)
if ensemble_type == "soft":
ensemble_test_pred = ensembling_soft(models, X_test)
else:
ensemble_test_pred = ensembling_hard(models, X_test)
ensemble_test_acc = accuracy_score(y_test_label, ensemble_test_pred)
global_hist["ensemble_test"].append(ensemble_test_acc)
print("Current Ensemble Test Accuracy : ", ensemble_test_acc)
global_hist["corrcoef"] = np.corrcoef(single_preds, rowvar=False)
print("Corr Matrix on each estimators (Test)")
print(global_hist["corrcoef"])
with open(f"ensemble_{ensemble_type}.dat", "wb") as fp:
pickle.dump(global_hist, fp)
if __name__ == "__main__":
K.clear_session()
train("soft")
モデルをリストに記録して、個々に訓練・推定して集約しているだけです。またval_accを基準にチェックポイントを作り、各モデルで最も精度の良いものを記録するようにしています。5個のネットワークを一気に訓練させる場合も試しましたが、普通のCNNに毛が生えたぐらいの違いでしかないので気になる方はこちらをご覧ください。
ここから次の3パターンを試します。
- 5個のCNNを別々に訓練し、ソフトなアンサンブルをする(確率の平均)
- 5個のCNNを別々に訓練し、ハードなアンサンブルをする(ラベルの多数決)
- 5個のCNNを同時に訓練する
ここで注意したいのは、5個のCNNは全て「同一の構造」「同一のデータ」「同一の損失関数」なのです。それでも今回の場合はアンサンブル学習はうまくいきます。
結果
ソフトなアンサンブルの場合
集計関数を「確率の平均」で定義した場合です。
| 分類器の数 | 単体の精度 | アンサンブル精度 |
|---|---|---|
| 1 | 0.8920 | 0.8917 |
| 2 | 0.8870 | 0.9012 |
| 3 | 0.8869 | 0.9032 |
| 4 | 0.8913 | 0.9071 |
| 5 | 0.8889 | 0.9096 |
数値はテスト精度です。アンサンブル精度はそれまでの分類器の結果を集計したものとなります。例えば分類器が3のときのアンサンブル精度は、1個目~3個目までの分類器の結果を集計したものです。
このように**単体の分類器では精度88~89%**なのに対して、アンサンブルをすると徐々に精度が上がり、5個つなげると91%近い精度を出すことができました。
分類器同士の推定ラベルの相関行列(相関係数を互いいとったもの)は次のようになりました。これはテストデータの推定ラベルに対して相関行列を取ったものです。
[[1. 0.90662105 0.90547762 0.91033771 0.90212712]
[0.90662105 1. 0.90322529 0.90978348 0.90214338]
[0.90547762 0.90322529 1. 0.90317076 0.89936101]
[0.91033771 0.90978348 0.90317076 1. 0.90522995]
[0.90212712 0.90214338 0.89936101 0.90522995 1. ]]
対角成分は同じ分類器同士の相関なので必ず1になります。先程の「相関係数が0.95以下ならアンサンブルする価値はある」という基準に照らし合わせると、どの相関係数も0.9程度なので、確かにこの基準を満たしていることがわかります。事実、アンサンブルの効果は出ています。
ハードなアンサンブルの場合
集計関数を「ラベルの多数決」で定義した場合です。
| 分類器の数 | 単体の精度 | アンサンブル精度 |
|---|---|---|
| 1 | 0.8899 | 0.8893 |
| 2 | 0.8898 | 0.8905 |
| 3 | 0.8862 | 0.9028 |
| 4 | 0.8903 | 0.9044 |
| 5 | 0.8898 | 0.9086 |
こちらもソフトの場合と同様に、単体では88~89%なのに対して、アンサンブルすると91%近い精度となりました。
ハードかソフトかどっちがよいかということについては、今回はほとんど誤差レベルなのでどちらでもよいのではないかという結論になりました。ただ、ハードつまり多数決の場合は、分類器の数を奇数にすべきだと思います。それは人間世界でも同じですよね。
ソフトな場合と同様に分類器同士の相関行列を見てみましょう。
[[1. 0.9044675 0.91135933 0.91168958 0.90222282]
[0.9044675 1. 0.90435752 0.90477526 0.90616101]
[0.91135933 0.90435752 1. 0.90708404 0.91213494]
[0.91168958 0.90477526 0.90708404 1. 0.91228747]
[0.90222282 0.90616101 0.91213494 0.91228747 1. ]]
こちらも相関行列が0.95以下ですよね。ハードな場合もアンサンブル効果は出ています。この行列は、単体の分類の精度にかなり依存するのではないかと思います。つまり、単体の分類精度がよほど高くなければ(95%や98%)でなければ、相関行列が0.95以下の基準を満たすのではないかということです。
しかし、これらは振り返ればもともと同一のニューラルネットワークのネットワーク、損失関数、データなので、全く同一のものから、分類精度が微妙に違う分類器が出来上がるという不思議な結果になります。一卵性双生児よりも遥かに似た育て方しているのに、それぞれわずかな違いが出てくるというのはなかなか不思議です。
この理由については、おそらくニューラルネットワークの訓練自体がかなり乱数を使っているので(重みの初期化やサンプルのシャッフル、ドロップアウトなど)、乱数の挙動が大きいのではないかなと思われます。つまり、どの分類器もグローバルな最適解に向かっているのだけれども、そこに向かう経路が違うからこういう差が出るのではないかということです。言い換えれば、単体の精度が100%に近づけば分類器同士の差は小さくなるでしょう。
5個のモデルを同時に訓練した場合
「でもこれってアンサンブルの効果じゃなくて、モデルが大きくなったから精度が良くなったんだよね?」という疑問も当然出てくるので、5個のモデルを同時に訓練してみました。
この場合のテスト精度は「0.8929」でしかありませんでした。
アンサンブルなしに同時に訓練しただけでは、91%近い精度を出すことはできませんでした。
まとめ
- 「同一の構造」のニューラルネットワークであっても、アンサンブル学習の有効性を確認できた
- ディープラーニングの場合は、単体のモデルの訓練からアンサンブルまで、End-to-Endな学習ができる
- 今回の場合は、単体のモデルの精度が極端に高くなかったので、ただそのままアンサンブルさせればよかった。しかし、95%や98%のような高精度なモデルをアンサンブルにより改善したい場合は、もっと弱い分類器を使ったり、別の構造のネットワークを使う、ピーキーな損失関数やデータの設定をするなどの工夫が必要そう。
ということでした。MAGIシステムのカスパーが裏切ったのは、赤木ナオコ博士の別々の人格を移植したからだということでしたが、もしかすると同一の人格を移植しても今回見たように差が出る、つまり「裏切り」が発生するということが起こるのかもしれません。もし興味があったら、小説や創作のネタにしてみてはいかがでしょうか。