レコメンド機能として用いられる協調フィルタリングをニューラルネットワークで実装してみました。ポケモンの種族値を「潜在的な特徴量」として、ユーザー(トレーナー)の評価の人工データを生成し、人工データから逆に推定することで「このポケモンが好きな人はこんなポケモンも好きです」というレコメンド機能を実装しました。ディープラーニングというほど深いモデルではありませんが、かなり良い結果を得ることができました。
リポジトリ:https://github.com/koshian2/Pokemon_NCF
元ネタ
元ネタの論文はこちら。シンガポール国立大学の先生が書いた論文。比較的読みやすいです。協調フィルタリングをニューラルネットワーク(NCF:Neural Collaborative Filtering)のアプローチから研究しています。
Xiangnan He, Lizi Liao, Hanwang Zhang, Liqiang Nie, Xia Hu, Tat-Seng Chua, Neural Collaborative Filtering, 2017
https://arxiv.org/pdf/1708.05031.pdf
協調フィルタリングは従来の機械学習では(講義の演習問題のノートですが以前書きました)、ニューラルネットワークを使わないで実装するのが普通です。協調フィルタリングのアルゴリズム自体、アイテム(商品や映画など)とユーザーのレビュー(アイテムに対する★1~★5といった点数)を、直接観測できない潜在的な特徴量を媒介して計算するという、かなりニューラルネットワークに近い発想です。「多分ニューラルネットワークでできるよなー」とググったら論文が出てきたという次第です。
今回実装するのはこの論文に出てくる最も簡単なモデルです。Matrix Factorizationはやりませんが、Matrix Factorizationもこのニューラルネットワークのアプローチからいけるとのことです。
協調フィルタリング
従来の協調フィルタリングでどうレコメンドを求めるのかを見ていきます。協調フィルタリングがわかっている方はここ飛ばして結構です。例えばですが、Aさん、Bさん、Cさんが寿司ネタを評価してみました。それぞれ0~5点までで評価しています。
| 寿司 | A | B | C |
|---|---|---|---|
| トロ | 4.75 | 0.25 | ? |
| 大トロ | 4 | ? | 3.4 |
| カツオ | ? | 0 | 4 |
| ヒラメ | 0 | ? | ? |
| タイ | ? | 4.75 | 1.15 |
「?」のところはそれぞれがまだ食べたことのない寿司ネタです。ここで3人にまだ食べたことのない寿司ネタをどの程度おすすめするのかを考えます。
Aさんの場合赤身が好きで白身は嫌いなようです。おそらくAさんにとってカツオは好まれて、タイは好まれないでしょう。Bさんの場合は逆に白身が好きで赤身は嫌いなようです。なので、Bさんにとっては大トロよりもヒラメをおすすめすべきです。Cさんの場合、Aさんほど極端ではないもののどちらかというと赤身のほうが好きそうです。Cさんにとってはヒラメよりもトロのほうが好まれそうです。
今やったことが協調フィルタリングのアルゴリズムです。協調フィルタリングとは与えられた好きか嫌いかの(レーティング)の情報から、未知のアイテム(この場合は寿司)のレーティングを推定するアルゴリズムです。教師あり学習の(訂正:CFは教師あり学習の要素もあるし、クラスタリングや主成分分析に似たところも多く教師なし学習の要素もあるので、一概に教師あり学習と断定はできないそうです。半教師あり学習だという意見もあります。)回帰問題です。?の推定結果をソートすれば、レコメンド機能つまり「○○が好きな人は○○もおすすめです」という、よくアマゾンで見られる機能に応用できます。
先程の寿司-ユーザーの表をYとします。表の要素を$y^{(i,j)}$、これはi番目の寿司ネタのj人目のユーザーの評価を表しましす。ただし$i\leq n_i, j\leq n_u$とします。今寿司ネタは5個、ユーザーは3人なので、$n_i=5, n_u=3$です。例えば、$y^{(2,1)}$はAさんの大トロの評価を表すため4となります。ただし$y^{(i,j)}$は評価がある場合のみ定義するので、Bさんの大トロに対する評価$y^{(2,2)}={\rm ?}={\rm undifined}$となります。問題設定はYの推定値つまり、$\hat{y}^{(i,j)}$を推定することです。
ではどう推定するのでしょうか?先程の例の場合、寿司ネタが赤身か白身か、A,B,Cが赤身・白身をどの程度好きかで評価しました。実は裏で以下のような計算をしました。
| 寿司 | 赤身 | 白身 |
|---|---|---|
| トロ | 0.95 | 0.05 |
| 大トロ | 0.8 | 0.2 |
| カツオ | 1 | 0 |
| ヒラメ | 0 | 1 |
| タイ | 0.05 | 0.95 |
数値は適当に与えたものですが、寿司ネタと赤身白身の対応を表す表です。この表の値をXとします。ここで赤身か白身かというのは潜在的な特徴量になります。$x_k^{(i)}$、これはi番目の寿司ネタのk番目の特徴量に対する係数となります。ただし、$k\leq K$。今特徴量は赤身か白身かという2つなので、$K=2$となります。例えば、$x_1^{(3)}$はカツオの赤身の係数なので1となります。
またユーザのクロスで見た潜在的な特徴量の表は次のとおりです。これはA,B,Cがどれだけ赤身、白身を好きかというものです。
| ユーザー | 赤身 | 白身 |
|---|---|---|
| A | 1 | 0 |
| B | 0 | 1 |
| C | 0.8 | 0.2 |
この表の値をΘとします。$\theta_k^{(j)}$は、j人目のユーザーのk番目の特徴量に対する値となります。例えば$\theta_1^{(3)}$は、Cさんの赤身に対する値なので0.8となります。
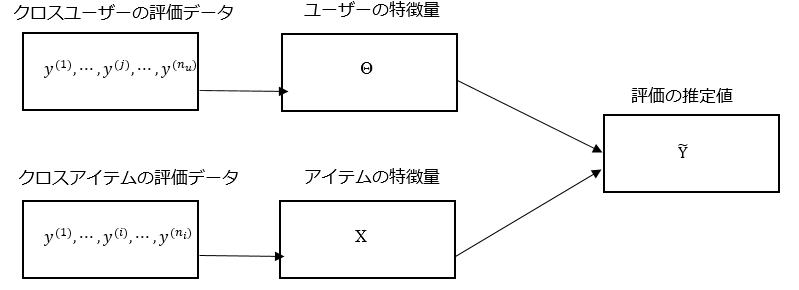
YはXとΘを使って次のように求められます。
$$Y = X\Theta^T * 5$$
例えば、Aさんのカツオに対する推定値$\hat{y}^{(3,1)}は、$
$$\hat{y}^{(3,1)}=x_1^{(3)}\theta_1^{(1)}+x_2^{(3)}\theta_2^{(1)} =(11+00)*5=5$$
となります。Aさんにカツオはとてもおすすめということですね。
実は、このXとΘというのは直接観測できない未知の値です。今説明のために特徴量を既知のものとして与えてしまいましたが、本来はユーザーの評価(Y)のみ観測できる値で、ユーザーの赤身、白身に対する好みというのは直接は観測できません。寿司ネタの赤身、白身の係数は外部から与えられるかもしれませんが、協調フィルタリングの場合特に与える必要はありません。XもΘも学習の過程でYから内生的に計算をすることができます。学習の過程でΘとXを交互に(協調的に)アップデートしていくため協調フィルタリングと呼ばれています。このような流れです。
目的関数は次の通りです。このJを最小化します。
\begin{align}
J&=\frac{1}{2}\sum_{i,j:r(i,j)=1}(\hat{y}^{(i,j)}-y^{(i,j)})^2 \\
r(i,j)&=\left\{\begin{array}{r}1 \qquad{\rm if}\quad y^{(i,j)}\neq{\rm undefined} \\ 0 \qquad{\rm if}\quad y^{(i,j)}={\rm undefined} \end{array}\right.
\end{align}
Yが定義されているもののみの誤差を取るというのが特殊ですが、誤差関数の中身は回帰分析と何ら変わりません。
従来の協調フィルタリングでは、ΘとXを媒介させることにだいぶ面倒な式や実装が入ります。しかし、ニューラルネットワークのアプローチでは、ニューラルネットワークの設計と目的関数を定義するだけであとは勝手に最適化してくれるので、割と簡単です。これを見ていきます。
ニューラルネットワークのアプローチ
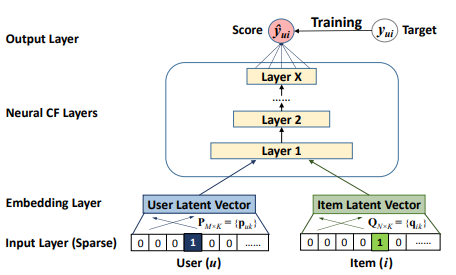
2つの入力を途中でマージするのがポイント。左側のNNは、ユーザーの特徴量の係数を検出しており、Θの係数を求めているのと同義です。右側のNNは、アイテムの特徴量を検出しており、Xの係数を求めているのと同義です。これらをマージし、全結合のレイヤーを組み合わせていくことで、評価の推定値$\hat{y}^{(i,j)}$を計算します。
この論文では全結合層のレイヤーを多層につなげていますが、従来の協調フィルタリングのアルゴリズムになぞらえるならここは内積(Kerasの場合Dotレイヤー)で一気に推定値までもっていっていいと思います。モデルが軽くなります。
左側のNNの入力層の次元はアイテムの数$n_i$に、右側のNNの入力層の次元はユーザーの数$n_u$となります。データの$Y$の次元は$(n_i, n_u)$なので、左側のNNの訓練データの数は$n_u$、右側のNNの訓練データの数は$n_i$と、2つのNNの間で訓練データの数が異なるというちょっと困ったことがおこります。しかし、総当たりで計算すれば特に問題はなさそうです。細かい実装は後ほど。
ポケモンのレコメンド
ここからが本題。誰がどのポケモンがおすすめというデータは聞いたことがありません。しかし、ポケモンにおける種族値を潜在的な特徴量とすれば人工的にレート(評価)のデータを作ることは可能です。
種族値
ポケモンには種類ごとにステータスを決定づける「種族値」という固有のパラメーターがあります。初代「ポケモン赤」の種族値を見ると以下の通りです(特攻、特防と別れていないのが時代を感じる)。
| 名前 | HP | 攻撃 | 防御 | 素早 | 特殊 |
|---|---|---|---|---|---|
| フシギダネ | 45 | 49 | 49 | 45 | 65 |
| フシギソウ | 60 | 62 | 63 | 60 | 80 |
| フシギバナ | 80 | 82 | 83 | 80 | 100 |
| https://pokemon.g-takumi.com/exertion_list.php |
この種族値をアイテム(ポケモン)の潜在的な特徴量とします。本来協調フィルタリングでは、潜在的な特徴量にこのような直接観察できる値を用いませんが、評価データを人工的に作るためにあえて用います。人工的にデータを作ったあとは、学習の際にこれらの特徴量は知らないふりをします。つまり、この人工的にデータを作るプロセスを逆にたどっていくと協調フィルタリングのプロセスになり、協調フィルタリングは今からやっていることの逆問題を解いているともいえるでしょう。
ただし、種族値は標準化して用います。今、種族値の値を$S_k^{(i)}, k\leq 5, i\leq n_i=151$、とします。種族値ごとの最大値で割って、それらのポケモンごとの係数の合計が1となるように標準化します。つまり、
$$X_k^{(i)}=\frac{1}{5}\frac{S_k^{(i)}}{\max_{l=1}^{n_i}S_k^{(l)}}$$
とします。上記の3ポケモンについて計算すると次の通りです。
| 名前 | HP | 攻撃 | 防御 | 素早 | 特殊 |
|---|---|---|---|---|---|
| フシギダネ | 0.18 | 0.365671642 | 0.272222222 | 0.321428571 | 0.422077922 |
| フシギソウ | 0.24 | 0.462686567 | 0.35 | 0.428571429 | 0.519480519 |
| フシギバナ | 0.32 | 0.611940299 | 0.461111111 | 0.571428571 | 0.649350649 |
これはspecies_normalized.csvにあります。
人工データ
次にトレーナー(ユーザー)単位の特徴量の行列を作ります。今作りたいのは、トレーナーがポケモンの各ステータスに対してどの程度価値をおいて判断しているかを表すデータです。今トレーナーを25人用意します($n_u=25$)。係数はランダムに入れてもいいのですが、極端な例があったほうが面白いので次のようにしました。
- 最初の5人は1つのステータス極振り。トレーナー1はHPだけ見る(HPだけ1で残りは0)、トレーナー2は攻撃だけ見る(攻撃だけ1で残り0)……
- 次の10人は2つのステータスを均等に見る。トレーナー6はHP0.5攻撃0.5で残りは0、トレーナー7はHP0.5防御0.5で残り0……、トレーナー15は素早さ0.5特殊0.5で残り0
- 次の5人は実践的にありそうな値を適当に入れてみた
- 最後の5人はトレーナー単位での係数の合計が1となるように正の乱数を入れてみる
今係数をかなり適当に与えてしまいましたが、種族値に対するトレーナーの係数の分布を知っていればブートストラップ法で係数行列を与えてもいいと思います。係数の行列を抜粋すると次のようになります。全てのデータはtrainer_features.csvにあります。
| ユーザー | 係数HP | 係数攻撃 | 係数防御 | 係数素早さ | 係数特殊 |
|---|---|---|---|---|---|
| トレーナー1 | 1 | 0 | 0 | 0 | 0 |
| トレーナー2 | 0 | 1 | 0 | 0 | 0 |
| トレーナー6 | 0.5 | 0.5 | 0 | 0 | 0 |
| トレーナー16 | 0 | 0.8 | 0 | 0.2 | 0 |
| トレーナー17 | 0.3 | 0.4 | 0 | 0.3 | 0 |
| トレーナー18 | 0.3 | 0 | 0 | 0.3 | 0.4 |
| トレーナー21 | 0.142306818 | 0.201214425 | 0.046424047 | 0.254790416 | 0.355264294 |
この行列をΘとします。Θの次元は$(n_u=25, 5)$となります。各トレーナーのポケモンに対する評価の人工データYは次のように計算します。
\begin{align}
A&=X\Theta^T \\
y^{(i, j)} &= {\rm round}(\frac{a^{(i,j)}}{\max{a^{(j)}}}, 0)*4+1
\end{align}
Aのi,j番目の要素は$a^{(i,j)}、$${\rm round}(z, 0)$はzの小数点以下を四捨五入を表します。特徴量どうしの内積を0~4の整数にマッピングして1を加える、つまり人工データで擬似的に与えられた評価は1~5の整数となります。トレーナーごとに最大評価が5になる保証がないのでスケール調整をしていますが、これはあってもなくてもどっちでもいいです。Yの行列の次元は$(n_i=151, n_u=25)$となりますが、最初の5×5の要素を抜き出すと次の通りです。
| 名前 | トレーナー1 | トレーナー2 | トレーナー3 | トレーナー4 | トレーナー5 |
|---|---|---|---|---|---|
| フシギダネ | 2 | 2 | 2 | 2 | 3 |
| フシギソウ | 2 | 3 | 2 | 3 | 3 |
| フシギバナ | 2 | 3 | 3 | 3 | 4 |
| ヒトカゲ | 2 | 3 | 2 | 3 | 2 |
| リザード | 2 | 3 | 2 | 3 | 3 |
全てのデータはdata.csvにあります。これで人工データが完成したので、いよいよニューラルネットワークの実装に入ります。
回帰問題として
レコメンド問題はレーティングをしていないデータ($y^{(i,j)}={\rm undefined}$)に対して、yの推定値を計算するものですが、先程作った人工データは全ての項目がレーティング済みです。今、レーティングしたかどうかはさておいて、ただの回帰問題として実装してみます。
前処理
データのcsvが3つあるので1つのNumpy配列になるように前処理します。
import numpy as np
import pandas as pd
# レーティングデータの読み込み
pd_data = pd.read_csv("data.csv",encoding="SHIFT-JIS")
# ポケモン名
pokemon_names = pd_data.values[:,0]
# レーティングデータ
data = pd_data.values[:,1:].astype(float)
# トレーナー別の特徴量係数の読み込み
pd_data = pd.read_csv("trainer_features.csv",encoding="SHIFT-JIS")
# トレーナー名
trainer_names = pd_data.values[:,0]
# 係数行列
trainer_coefs = pd_data.values[:, 1:]
# ポケモン別の特徴量(種族値)の読み込み
pd_data = pd.read_csv("species_normalized.csv",encoding="SHIFT-JIS")
# 種族値
pokemon_spicies = pd_data.values[:,1:]
# あとから読みやすいようにNumpy配列として保存
np.savez("data", data=data, pokemon_names=pokemon_names, pokemon_spicies=pokemon_spicies,
trainer_names=trainer_names, trainer_coefs=trainer_coefs)
種族値のデータも読んでいますが、学習の過程で使うことはありません。
ニューラルネットワークの実装
以下のようなネットワークを作ります。
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) (None, 151) 0
__________________________________________________________________________________________________
input_2 (InputLayer) (None, 25) 0
__________________________________________________________________________________________________
dense_1 (Dense) (None, 5) 760 input_1[0][0]
__________________________________________________________________________________________________
dense_2 (Dense) (None, 5) 130 input_2[0][0]
__________________________________________________________________________________________________
dot_1 (Dot) (None, 1) 0 dense_1[0][0]
dense_2[0][0]
==================================================================================================
Total params: 890
Trainable params: 890
Non-trainable params: 0
__________________________________________________________________________________________________
人工データの作成過程では、種族値という潜在的な特徴量からレーティングを線形関数で作ったので、逆問題であるInput1、Input2から特徴量へのマッピングも明らかに線形となります。したがって、Input1,Input2への全結合層は1つでよいことがわかります。より人工データではなく、実際のデータで特徴量が線形関数で抽出できない場合はここを深くしてもいいと思います。
Denseで5ずつ変形したのち、2つのネットワークをDot(内積)で結合します。論文の図ではここは複数の全結合層で表現していましたが、どっちみち似たような計算になるはずなので、最初から内積を与えたほうが計算が速いと思います。ただし、レーティングが特徴量同士の線形結合で表現できない場合は、論文通りに深くする意味があるのではないかと思います。コードで書くと次のようになります。
import numpy as np
from keras.layers import Input, Dense, Dot
from keras.models import Model
from keras.optimizers import Adam
# 先にpreprocess.pyを実行してNumpy配列を作っておく
pokemon = np.load("data.npz")
# 定数
n_pokemon, n_trainer = pokemon["data"].shape #(151, 25)
# トレーナー別のポケモンに対するレーティングを入力するモデル input_shape=(151,)
input_a = Input(shape=(n_pokemon, ))
# 特徴量にマッピング
x_a = Dense(5, activation="relu")(input_a)
# ポケモン別のユーザーごとのレーティングを入力するモデル input_shape=(25,)
input_b = Input(shape=(n_trainer, ))
# 特徴量にマッピング
x_b = Dense(5, activation="relu")(input_b)
# モデルを結合(ここでは内積を取る)
y = Dot(axes=-1)([x_a, x_b])
# コンパイル
model = Model(inputs=[input_a, input_b], outputs=y)
model.compile(optimizer=Adam(lr=0.0001), loss="mse", metrics=["mse"])
追記:x_a, x_bの活性化関数、reluではなくtanh関数ほうがいいかもしれません。特に中間層の出力を取りたい場合、reluだと結構潰れます。試してみた限りでは、シグモイド関数→収束遅い、線形→誤差は少ないけどスケールの保証がないのと隠れ層を入れる場合は意味がない、tanh→線形に近い誤差までは落ちて案外いい感じ。
ただし、いつものようにX,yとfitさせるのではなく、Yを行と列の双方向でfitさせる必要があるので、通常のfit関数が使えません(行列を複製すればfitが使えるがそれではメモリ効率が悪い)。そこでfit_generatorを自作します。
fit_generator
# fit_generator
def fit_gen(data):
global n_pokemon, n_trainer
while True:
for i in np.random.permutation(n_pokemon):
for j in np.random.permutation(n_trainer):
# 1ランクのベクトルになるのでreshapeで2ランクにすること
yield [data[:,j].reshape(1,-1), data[i,:].reshape(1,-1)], data[i,j].reshape(1,-1)
# generatorを使ってフィット
model.fit_generator(generator=fit_gen(pokemon["data"]),
steps_per_epoch=n_pokemon*n_trainer, epochs=10)
ここがハマリどころで、reshape(1, -1)をしないと「次元が違うよ」と怒られます。これはYのスライスがベクトル(1ランク)であることによるものです。Pythonの言語仕様上、1ランクのベクトルをそのまま使うと奇妙な計算が起こる(例:ベクトルの転置がそのままになる)ので、バグ予防のために2ランク以上を要求しているのだと思います。reshapeすれば何の問題もないので直しましょう。
ジェネレーターは無限ループの形で定義して、あとは組み合わせ的に行と列のスライスをジェネレーターとして返しているだけです。forループのインデックスを順列(permutation)として返しているので、インデックスのシャッフル機能もあります。うまく収束しないときは学習率を調整しましょう(たいてい大きすぎる)。
CPUで1epoch7秒程度で計算できます。10epochしても1分ちょいです。ではデータと推定値を比較してみましょう。嗜好がHP、攻撃、防御……の各ステータス極振りのトレーナー1~5のピカチュウに対するレーティングの推定値を計算してみます。
# HPしか興味ない人(トレーナー1)のピカチュウのレーティングは?
pred_24_0 = model.predict([pokemon["data"][:,0].reshape(1,-1), pokemon["data"][24,:].reshape(1,-1)])
# 攻撃しか興味ない人(トレーナー1)のピカチュウのレーティングは?
pred_24_1 = model.predict([pokemon["data"][:,1].reshape(1,-1), pokemon["data"][24,:].reshape(1,-1)])
# 以下略
print("予測結果")
print("トレーナー1(HP)のピカチュウのレートのデータは、", pokemon["data"][24,0])
print("トレーナー1(HP)のピカチュウのレートの予測値は、", pred_24_0)
# 以下略
結果は以下の通り。なかなか良さそうです。トレーナー4だけかなり乖離がありますが、epoch数を増やせばなんとかなるでしょう。
3775/3775 [==============================] - 5s 1ms/step - loss: 0.5702 - mean_s
quared_error: 0.5702
予測結果
トレーナー1(HP)のピカチュウのレートのデータは、 2.0
トレーナー1(HP)のピカチュウのレートの予測値は、 [[1.788103]]
トレーナー2(攻撃)のピカチュウのレートのデータは、 3.0
トレーナー2(攻撃)のピカチュウのレートの予測値は、 [[3.095326]]
トレーナー3(防御)のピカチュウのレートのデータは、 2.0
トレーナー3(防御)のピカチュウのレートの予測値は、 [[2.2915573]]
トレーナー4(素早さ)のピカチュウのレートのデータは、 4.0
トレーナー4(素早さ)のピカチュウのレートの予測値は、 [[2.5494237]]
トレーナー5(特殊)のピカチュウのレートのデータは、 2.0
トレーナー5(特殊)のピカチュウのレートの予測値は、 [[2.6407263]]
NCFによるポケモンのレコメンド
さて、実際のレコメンドでは評価がundefinedな項目に対して予測がほしいわけです。これをどう実装するかを見ていきます。
損失関数のカスタマイズ
結論から言うと、fit_generatorのほかに損失関数も自作する必要があります。損失関数の引数がy_true, y_predの形式で与えられるので、y_trueでundefinedを検出できればいいわけです。トリッキーなやり方ですが次のように計算しました。
# より実践的な例にするために未評価の項目を入れる
np.random.seed(151)
rand = np.random.uniform(size=(n_pokemon, n_trainer))
# 乱数が0.6以下なら未評価とする
mask = (rand > 0.6).astype(int)
data = pokemon["data"]
data[mask==0] = 0
まずはモンテカルロ法で6割の確率で評価されていないようにします。maskの変数が1なら評価済み、0なら未評価とします。未評価のyを0とします。協調フィルタリングではポケモン単位で標準化しておくと、どのポケモンを評価していないトレーナーが現れた場合に、レーティングの平均値を返すという便利なトリックがあるので、平均標準化と「未評価=y=0」を両立したいのです。なぜ未評価=y=0が便利かというと、損失関数を次のように定義すればいいからです。
$$L(\hat{y}, y)=[{\rm sgn}(y)]^2(\hat{y}-y)^2 $$
ここで${\rm sgn}(z)$は符号関数です。符号関数の2乗は0以外なら1、0のみ0となるので、0に対するちょうどいいマスクになるからです。符号関数は幸いKeras.backend.signで使えます。
ここで注意しなければいけないのは、評価済みだが0になっている値と、未評価なため0になっている値を区別しなければいけないことです。そこで前者に対しては、結果に対してほとんど影響が出ないような微小な値ε(例:$\epsilon=10^{-8}$)を代入します。いくら微小な値といえど0ではないので、${\rm sgn}(\epsilon)=1$となります。これでできそうです。
# ポケモンごとの平均値を計算
avg = np.zeros(n_pokemon)
for i in range(n_pokemon):
slice = data[i, mask[i, :]==1]
if(len(slice) > 0):
avg[i] = np.mean(slice)
# 観測値から平均値を引く
data = (data - np.tile(avg, (n_trainer, 1)).T) * mask
# データありで0になってしまったところに微小量を加える
data[(mask==1) & (data==0)] = 1e-8
損失関数は次のようになります。
import keras.backend as K
# カスタム損失関数
def loss_function(y_true, y_pred):
squared = K.square(y_true - y_pred)
# sign(0)=0, sign(正の数)=1、sign(負の数)=-1なので、sign関数の2乗で未評価の項目をフィルタリングできる
return squared * K.square(K.sign(y_true))
ニューラルネットワークの実装は共通なので省略します。詳しくはコード全文を見てください。
訓練
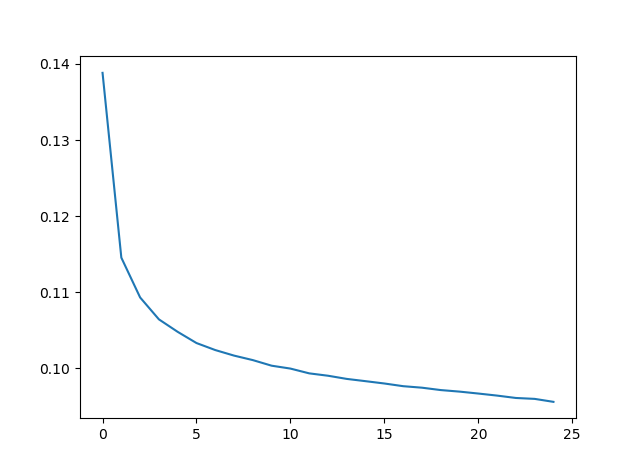
25epochさせて訓練してみました。CPUで1周6~7秒で終わるので、3分もあれば訓練終わります。
# コンパイル
model.compile(optimizer=Adam(lr=0.0001), loss=loss_function)
# generatorを使ってフィット
n_epochs = 25
history = model.fit_generator(generator=fit_gen(data),
steps_per_epoch=n_pokemon*n_trainer, epochs=n_epochs).history
plt.plot(np.arange(n_epochs), history["loss"])
plt.show()
おすすめのポケモン
では実際におすすめのポケモンを表示してみます。
攻撃極振りのトレーナー2の場合
# おすすめのポケモンを上位10件表示
def recommendation_view(pred, mask, avg):
global pokemon
# 評価済みポケモン
print("評価済みポケモン")
print(pokemon["pokemon_names"][mask==1])
# 予測レート
score = (pred + avg) * (1-mask)
# ポケモンのインデックス
index = np.argsort(score)[::-1][:10]
cnt = 1
print("おすすめのポケモン一覧")
for i in index:
if mask[i] == 1: break
print(cnt, "位 : id =", i+1, "(", pokemon["pokemon_names"][i], ")", "予測レート :", score[i])
cnt += 1
print()
# 予測
def recommendation(column_id):
pred = model.predict([np.tile(data[:,column_id], (n_pokemon, 1)), data])
# おすすめ表示
recommendation_view(np.ravel(pred), mask[:,column_id], avg)
# 攻撃極振りが好きなトレーナー2の場合
print("-攻撃極振りのトレーナー2の場合")
recommendation(1)
print()
-攻撃極振りのトレーナー2の場合
評価済みポケモン
['フシギソウ' 'ヒトカゲ' 'リザード' 'リザードン' 'ゼニガメ' 'カメックス' 'キャタ
ピー' 'トランセル' 'ビードル'
'コクーン' 'オニドリル' 'アーボ' 'アーボック' 'ライチュウ' 'サンド' 'サンドパン
' 'ニドクイン' 'ニドラン♂'
'ニドリーノ' 'プリン' 'プクリン' 'ズバット' 'ゴルバット' 'パラセクト' 'ダグトリ
オ' 'コダック' 'ゴルダック'
'ウインディ' 'ユンゲラー' 'ゴーリキー' 'カイリキー' 'ウツドン' 'ドククラゲ' 'ゴ
ローン' 'ポニータ' 'ヤドラン' 'コイル'
'レアコイル' 'カモネギ' 'ジュゴン' 'ベトベトン' 'ゴースト' 'クラブ' 'ガラガラ'
'ベロリンガ' 'マタドガス' 'サイホーン'
'モンジャラ' 'タッツー' 'シードラ' 'ヒトデマン' 'ストライク' 'エレブー' 'カイロ
ス' 'ケンタロス' 'メタモン'
'シャワーズ' 'ポリゴン' 'オムナイト' 'カブト' 'サンダー' 'ハクリュー' 'ミュウ'
おすすめのポケモン一覧
1 位 : id = 150 ( ミュウツー ) 予測レート : 4.906726540281222
2 位 : id = 130 ( ギャラドス ) 予測レート : 4.66666896475686
3 位 : id = 136 ( ブースター ) 予測レート : 4.502372097969055
4 位 : id = 142 ( プテラ ) 予測レート : 4.382128940688239
5 位 : id = 106 ( サワムラー ) 予測レート : 4.356381470506841
6 位 : id = 85 ( ドードリオ ) 予測レート : 4.347608978931721
7 位 : id = 141 ( カブトプス ) 予測レート : 4.334814718791417
8 位 : id = 112 ( サイドン ) 予測レート : 4.185151010751724
9 位 : id = 91 ( パルシェン ) 予測レート : 4.101234656572342
10 位 : id = 135 ( サンダース ) 予測レート : 4.080316826701164
ミュウツーは全部強いからまだしも、ブースター、プテラ、サワムラーといった攻撃特化のポケモンがおすすめされていますね。
防御極振りのトレーナー3の場合
# 防御極振りが好きなトレーナー3の場合
print("-防御極振りのトレーナー3の場合")
recommendation(2)
print()
同様に防御重視のトレーナーに対するレコメンドを見てみます。
-防御極振りのトレーナー3の場合
評価済みポケモン
['フシギソウ' 'キャタピー' 'バタフリー' 'スピアー' 'ポッポ' 'ピジョット' 'コラッ
タ' 'ラッタ' 'アーボ' 'ライチュウ'
'サンド' 'ニドラン♀' 'ニドクイン' 'キュウコン' 'プリン' 'プクリン' 'ナゾノクサ
' 'クサイハナ' 'パラス' 'コンパン'
'モルフォン' 'ディグダ' 'ニャース' 'ペルシアン' 'オコリザル' 'ニョロモ' 'ニョロ
ゾ' 'ニョロボン' 'ゴローン' 'ポニータ'
'ヤドン' 'コイル' 'ドードー' 'パウワウ' 'ジュゴン' 'パルシェン' 'ゴース' 'ゴー
スト' 'キングラー' 'マルマイン'
'タマタマ' 'カラカラ' 'ベロリンガ' 'サイドン' 'ラッキー' 'ガルーラ' 'タッツー'
'ヒトデマン' 'バリヤード' 'ストライク'
'ブーバー' 'ラプラス' 'オムスター' 'カブトプス' 'プテラ' 'フリーザー' 'ファイヤ
ー' 'ミュウツー' 'ミュウ']
おすすめのポケモン一覧
1 位 : id = 130 ( ギャラドス ) 予測レート : 4.222222222222222
2 位 : id = 103 ( ナッシー ) 予測レート : 4.0
3 位 : id = 149 ( カイリュー ) 予測レート : 4.0
4 位 : id = 135 ( サンダース ) 予測レート : 4.0
5 位 : id = 145 ( サンダー ) 予測レート : 4.0
6 位 : id = 85 ( ドードリオ ) 予測レート : 3.923076923076923
7 位 : id = 59 ( ウインディ ) 予測レート : 3.909090909090909
8 位 : id = 94 ( ゲンガー ) 予測レート : 3.888888888888889
9 位 : id = 3 ( フシギバナ ) 予測レート : 3.857142857142857
10 位 : id = 121 ( スターミー ) 予測レート : 3.8
防御極振りはあまりうまく行かなくて、イワーク、ゴローニャといった固いポケモンがトップに出てきませんでした。
ロケット団におすすめのポケモンを探す
人工データに対するリコメンドを計算しても面白くないので新規のユーザーを対象にしてみましょう。アニメのロケット団に登場していただきます。
Wikipediaのムサシ、コジロウによると、無印編では次のポケモンを使用したそうです。以下の条件でレーティングを入力します。
- 進化のあるポケモンは進化前を4点、進化後を5点とする。進化のないポケモンは5点とする。進化前を捕まえてなければ点数は入力しない。
- ムサシ:アーボ4点、アーボック5点、ベロリンガ5点、シェルダー5点として入力
- コジロウ:ドガース4点、マタドガス5点、ガーディー4点、ウツドン4点、ウツボット5点として入力。コイキングとギャラドスは除外。
- ニャースはおすすめする側なのかおすすめされる側なのかわからないので除外
# ロケット団のポケモンを入れてみる
rocket_score, rocket_mask = np.zeros(n_pokemon), np.zeros(n_pokemon)
# アーボ(22)は4点、アーボック(23)は5点
rocket_score[22], rocket_score[23] = 4, 5
rocket_mask[22], rocket_mask[23] = 1, 1
# ベロリンガ(107)も5点
rocket_score[107], rocket_mask[107] = 5, 1
# シェルダー(89)は4点
rocket_score[89], rocket_mask[89] = 4, 1
# ドガース(108)は4点、マタドガス(109)は5点
rocket_score[108], rocket_score[109] = 4, 5
rocket_mask[108], rocket_mask[109] = 1, 1
# ガーディ(57)は4点
rocket_score[57], rocket_mask[57] = 4, 1
# ウツドン(69)は4点、ウツボット(70)は5点
rocket_score[69], rocket_score[70] = 4, 5
rocket_mask[69], rocket_mask[70] = 1, 1
# 標準化
rocket_score = rocket_score - avg
rocket_score[(rocket_score==0) & (rocket_mask==1)] = 1e-8
# おすすめ表示
print("-ロケット団の場合")
rocket_pred = model.predict([np.tile(rocket_score, (n_pokemon, 1)), data])
recommendation_view(np.ravel(rocket_pred), rocket_mask, avg)
結果は以下のとおりです。
-ロケット団の場合
評価済みポケモン
['アーボ' 'アーボック' 'ガーディ' 'ウツドン' 'ウツボット' 'シェルダー' 'ベロリン
ガ' 'ドガース' 'マタドガス']
おすすめのポケモン一覧
1 位 : id = 68 ( カイリキー ) 予測レート : 4.972293901443481
2 位 : id = 150 ( ミュウツー ) 予測レート : 4.928147346927569
3 位 : id = 127 ( カイロス ) 予測レート : 4.924015998840332
4 位 : id = 130 ( ギャラドス ) 予測レート : 4.735909057988061
5 位 : id = 136 ( ブースター ) 予測レート : 4.627373230457306
6 位 : id = 123 ( ストライク ) 予測レート : 4.561054853292612
7 位 : id = 106 ( サワムラー ) 予測レート : 4.539365941827947
8 位 : id = 142 ( プテラ ) 予測レート : 4.476280437575446
9 位 : id = 85 ( ドードリオ ) 予測レート : 4.413746590797718
10 位 : id = 141 ( カブトプス ) 予測レート : 4.409230938979558
なかなか渋い面子が出てきました。ロケット団への一押しは「カイリキー」ということになりました。ストライクよりもカイロスが上にきているのが面白いです。
注意点
ニューラルネットワークの結果はepoch数や初期の乱数で変わるので、実行のたびに結果が上下することがあります。従来の協調フィルタリングでも最急降下法を用いるため、同様の結果の不安定さは変わりません。
ただ、このようにニューラルネットワークのアプローチでも、数値でおすすめのポケモンを計算できたことは意義があると思います。今回扱った人工データは論文に載っていたものではなく自分が勝手に作ったものですが、かなり応用例はありそうな気はします。