2021年のディープラーニング論文を1人で読むAdvent Calendar18日目の記事です。今日読む論文は「不均衡データの対策」です。この研究は、不均衡データにおける局所的な過学習に着目し、決定境界の近くにあるサンプルのウェイトを下げることで、不均衡データの訓練における副作用を緩和するというチャレンジングな内容です。
一見難しそうに見えますが、実装上はクロスエントロピーで一定期間訓練したら、提案手法のロスでファインチューニングするだけという実装的にやりやすい方法です。データレベルやネットワーク構造を変更することなく、ロスの変更だけで一貫した精度上を見込めます。理論と実装が一貫したなかなか良い論文です。著者はソウル大学校の方で、論文はICCV2021に採択されていきます。読んでいきましょう。
- タイトル:Influence-Balanced Loss for Imbalanced Visual Classification
- URL:https://openaccess.thecvf.com/content/ICCV2021/html/Park_Influence-Balanced_Loss_for_Imbalanced_Visual_Classification_ICCV_2021_paper.html
- 出典:Seulki Park, Jongin Lim, Younghan Jeon, Jin Young Choi; Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2021, pp. 735-744
- コード:https://github.com/pseulki/IB-Loss
不均衡データってどういうの?
精度94.3%の分類器ができました→ちょっと待ってください!
不均衡データとはこういう例です。クラス単位でデータ数に異常なばらつきがある例です。
| クラスA | クラスB | クラスC | |
|---|---|---|---|
| データ数 | 5000 | 100 | 25 |
| クラス精度 | 95% | 70% | 50% |
5000×95% + 100×70% + 25×50% ÷ (5000+100+25) = 94.3%
何も考えずに、正解数÷失敗数を計算すると、この値(micro average)が計算されます。Kerasのプログレスバーで表示される値はこれです。しかし、この94.3%が嬉しいかというと、あんまり嬉しくはないですよね。クラスBやCを見分けることが重要な意味合いを持っていたらどうでしょうか? 次の表のほうが嬉しいことも多いです。
| クラスA | クラスB | クラスC | |
|---|---|---|---|
| データ数 | 5000 | 100 | 25 |
| クラス精度 | 90% | 80% | 65% |
クラスAは5%下がってしまいましたが、クラスBは+10%、クラスCは+15%になりました。実は先程のmicro averageによる精度を計算すると、
5000×90% + 100×80% + 25×65% ÷ (5000+100+25) = 89.7%
5%近く下がっています。全体の精度が下がったほうが嬉しい、ちょっとおかしいですよね。
microとmacro
この感覚のズレを解消するために、macro averageによる精度を計算します。macro averageとはクラス単位の精度を単純平均で求めます1。
- 前者:(95% + 70% + 50%) ÷ 3 = 71.7%
- 後者:(90% + 80% + 65%) ÷ 3 = 78.3%
直感と一致しました。microを使うか、macroを使うかは問題によりけりです。macro averageで集計するコンペもあります。不均衡データ対策ではこのような改善をしたいのです。
不均衡データの改善の問題スコープ
ここで問題スコープを整理しましょう。
- micro average(サンプル単位)ではある程度の精度を出しているが、macro average(クラス単位)では少数データのクラスが足を引っ張って精度を出せていない
- micro averageは下がっても構わないから、macro averageを上げてほしい
これが本論文を含めた不均衡データの問題のスコープです。本論文の手法を導入すればmicroもmacroも上がる、ということはないとは言いませんがかなりの確率で保証されません。
問題設定として、「microで上がってほしいのか、macroで上がってほしいのか」をまず見極める必要があります。今回紹介する論文は、問題設定がこのスコープ内にあるときはとても便利な手法です。
不均衡データの具体例
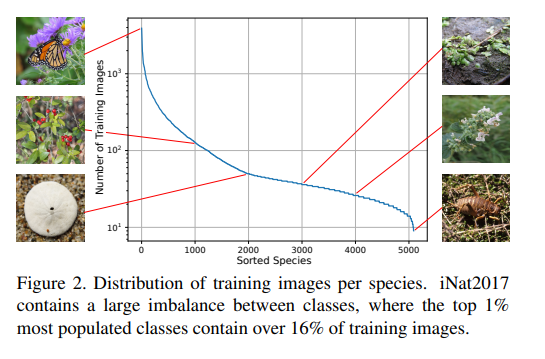
リアルのデータではたびたびありますが、研究データセットとしてはiNaturalistが有名です。
iNaturalistは自然界の動植物を種ごとに分類したものです。蝶は1000枚以上ありますが、最も少ない(謎の)虫は1クラス10枚程度です。自然界の動植物はよく見かける種から、レアな種までバラバラなので、不均衡データの一例です。
本論文の手法の要点
普通に訓練して「Influence-balanced loss」でファインチューニング
本論文はファインチューニングで不均衡問題をなんとかしようとしています。最初に普通にクロスエントロピーで訓練します。訓練が進んだら本論文の提唱手法である「Influence-balanced loss」でファインチューニングします。擬似コードでは次のとおりです。
Phase1は普通の画像分類です。Phase2が不均衡なクラスに対する調整で、分母にIB weighting factorという何らかの係数をかけているものと思ってください。ロスを変えたただのファインチューニングなので、サンプル方法やネットワーク構造が変わるといったことは変わりません。
不均衡にしたCIFAR-10でどれぐらい変わるのか
理論は後回しにして結果から見ていきます。CIFAR-10の訓練サンプル数だけ不均衡にして評価しています。テストサンプル数は各クラス1000です。
不均衡のタイプが2パターン用意されていて、(1)ロングテール (2)ステップ不均衡です。ロングテールはiNaturalistのように、指数関数的に減っていくパターンを模擬して作った不均衡。ステップ不均衡は、半分のクラスだけ訓練サンプル数を100にしまうという人為的な設定です。
Baseline(CE)というのがクロスエントロピーによる訓練で、ステップ不均衡の例では、少数サンプルのクラスに対し、精度2~5割というかなりひどい結果になっています。本論文の提唱手法を使ったのがIB以下で、IBを使うと不均衡側が2~3割アップ、Focal lossまで合わせて使うと概ね数%~5%上がる傾向にあります。ただし、均衡側の精度は数%落ちるので、先程の問題スコープで確認したとおり、micro/macro全体で上げてほしいという虫のいい話ではありません。
ちなみにコードは
これだけ。公式コードより
def ib_loss(input_values, ib):
"""Computes the focal loss"""
loss = input_values * ib
return loss.mean()
class IBLoss(nn.Module):
def __init__(self, weight=None, alpha=10000.):
super(IBLoss, self).__init__()
assert alpha > 0
self.alpha = alpha
self.epsilon = 0.001
self.weight = weight
def forward(self, input, target, features):
grads = torch.sum(torch.abs(F.softmax(input, dim=1) - F.one_hot(target, num_classes)),1) # N * 1
ib = grads*features.reshape(-1)
ib = self.alpha / (ib + self.epsilon)
return ib_loss(F.cross_entropy(input, target, reduction='none', weight=self.weight), ib)
不均衡対策には3つのアプローチがある
本論文によると、不均衡対策にはこれまで3つのアプローチからなります。
- データレベルのアプローチ:オーバーサンプリング、アンダーサンプリング、データの生成が例です。アンダーサンプリングは重要な情報を失う可能性があり、不均衡が大きい場合は不敵。オーバーサンプリングや生成は、特定の繰り返しのサンプルに過学習する可能性があり、訓練時間が長くなる
- コストに応じた再重み付けのアプローチ:クラス数に反比例or頻度の平方根となるような、定数を割り当てるのがオーソドックスな方法。サンプル単位の重要度は関係なくクラス単位で同一の重み付けをするというデメリットがある。サンプルの困難度や損失に応じた重み付けが多数提案されている。
- メタ学習のアプローチ:十分な性能を得ることができるが、実装が困難
本論文の手法は、サンプル単位の再重み付けのアプローチに位置します。損失関数を変えてファインチューニングするだけなので、他のサンプリング、重み付け、メタ学習といった不均衡対策の論文手法と容易に併用できるというメリットがあります。
理論解説
不均衡の問題は、局所的な決定境界の過学習にあり
本論文のアウトラインを紹介したので、どのようにしてInfluence-balanced lossが生まれたかを見ていきましょう。数式による導入の前に提案手法のお気持ちを理解していきましょう。
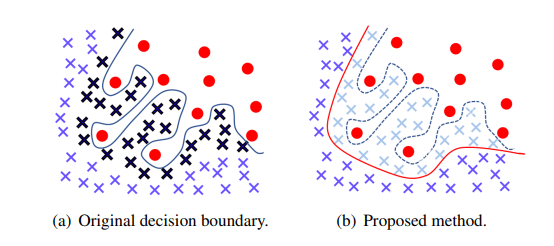
これが本論文のキーコンセプトです。クロスエントロピーで訓練したのが左図です。
不均衡データに対して精度が落ちてしまうのは、少数サンプルのクラスがある関係で、局所的に決定境界がぐにゃぐにゃになり、部分的な過学習を起こしてしまうからです。これをどうにかして右のような状態に持っていきたいのです。「黒い☓」のようなサンプルは決定境界に大きな影響があります。理想的には決定境界に大きな影響を与えるサンプルがなければいいのです。
具体的には、決定境界に大きな影響を与える(b)の「薄青の☓」のサンプルをダウンウェイトさせるような係数を作ります。こうしてできたのがIB weighting factorやInfluence-balanced lossです。局所的な過学習と決定境界の平滑化がこの論文の大きなコンセプトです。
IB weighting factor
$i$番目の訓練画像を$x_i$、ラベルを$y_i$とし、$f(x, w)$をニューラルネットワークの出力とします。損失関数を$L(y_i, f(x_i, w))$とします。このとき経験リスクは、
$$R(w)=\frac{1}{n}\sum_{i=1}^n L\bigl(y_i, f(x_i, w)\bigr)$$
となります。最適なパラメーター$w^*$は$\arg\min_w R(w)$として表されます。ファインチューニング中に決定境界に近いサンプルを取り除くものとして、その影響度を$w_{x, \epsilon}$とすれば、
$$e_{x, \epsilon}=\arg\min_w R(w)+\epsilon L\bigl(y_i, f(x_i, w)\bigr)$$
と定義します。ここで最適なパラメーター$w^*$の近傍では$\nabla_w R(w)\approx 0$になることを考えると(ロスが最小化された状態では勾配がほぼ0になることをイメージしてください)、**影響関数(Influence function)**は、
\mathcal{I}(x; w)=-H^{-1}\nabla_w L\bigl(y, f(x, w)\bigr)\tag{1} \\ H=\frac{1}{n}\sum_{i=1}^n \nabla^2_w L\bigl(y, f(x, w)\bigr)
影響関数は先行研究であったものです。サンプル単位のロスを再重み付けするためにこのような関数を導入しています。$H$はヘッセ行列です。
最適なパタメーター$w^*$周辺では、局所的な凸状のくぼみになっているわけですが、ここで$L$が狭義凸関数であるという仮定に基づき$H$は正定値となります(狭義凸関数のヘッセ行列は正の定数となります:参考)。
式(1)では損失関数のヘッセ行列の逆行列を計算しないといけませんが、これは非常に計算量が大きくなってしまうので、なんとか無視する方法を考えます。実装上は、バッチ内の全サンプルを通じたロスを計算したあと平均をとってから微分や偏微分を計算するため、ヘッセ行列が全サンプルに共通して掛けられる値となります。ヘッセ行列はただの定数となるため、ヘッセ行列の逆行列の部分は無視できることになります。ここでIB weighting factorを、
$$\mathcal{IB}(x;w)=|\nabla_w L\bigl(y_i, f(x_i, w)\bigr)|_1 \tag{2}$$
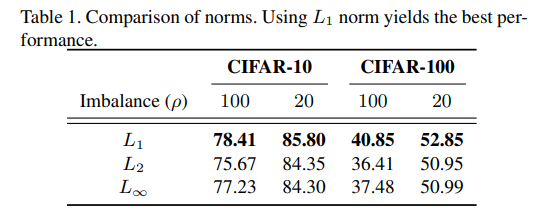
とします。先行研究では、不均衡問題では誤差の勾配ベクトルが主要クラスによって支配されることがわかっています。そこで、勾配ベクトルの大きさで再重み付けするということをしています。過学習した決定境界の近傍にあるサンプルはこの値が大きくなるので、ロスをIB weighting factorで割れば、過学習につながるサンプルの割合を下げることができます。ここでノルムの関数ですが、実験ではL1ロスが一貫して良いことが調べられています。
損失関数へ
式(2)のままでも損失関数としてはいけるのですが、Backpropとあわせて2回微分が必要になるのでもう少し解析的に分解します。いま最終層の入力特徴量が$h=[h_1, \cdots, h_L]^T$というベクトルで表されたとします。ここで出力$f(x, w)=[f_1, \cdots, f_K]^T$の$f_k$は、出力層の係数$w=[w_1, \cdots, w_K]^T \in \mathbb{R}^{K\times L}$を用いて、
$$f_k=\sigma(w_k^T h)$$
で表されます。ここで$\sigma$はソフトマックス関数です。ソフトマックス関数とクロスエントロピーの微分(こちらの記事が参考になります)より、
$$\frac{\partial}{\partial w_{kl}}L\bigl(y, f(x, w)\bigr)=(f_k-y_k)h_l$$
です。ただ、これはソフトマックスクロスエントロピーだけでなく、シグモイドやMSEでも同じ結果になるとのことです。これにより、式(2)のIB weighting factorの微分を消せます。
\begin{align}\mathcal{IB}(x;w)&=\sum_k^K \sum_l^L |(f_k-y_k)h_l|\\&=\sum_k^K|(f_k-y_k)|\sum_l^L|h_l|\\&=\|f(x,w)-y\|_1\cdot\|h\|_1 \end{align}
分類問題なら第1項は予測確率とラベルのOne-hot値の差の絶対値を、クラス間で合計したものを表します。差の絶対値は$(N, K)$という次元ですが、$K$について和をとり$N$次元のベクトルになります。
第2項はバックボーンのネットワークのGlobal Average Pooling直後の$(N, D)$という特徴量に対し、絶対値をとり$D$の次元で和をとったものを表します。こちらも$N$次元のベクトルです。したがって、IB weighting factorは$N$次元のベクトルになります。サンプル単位の再重み付けの値を示すので、定義にマッチしますね。
ここで本論文のコア手法であるInfluence-balanced lossが登場します。これはとてもシンプルで、クロスエントロピーのロスをIB weighting factorで割るだけです。
$$L_{IB}\bigl(y, f(x, w)\bigr)=\frac{L\bigl(y, f(x, w)\bigr)}{|f(x,w)-y|_1\cdot|h|_1} \tag{3}$$
最初に見たときは「何このロス」感ありましたが、ゆっくり理論展開を追っていくと「なるほど」感のある損失関数です。
Influence-balanced lossとFocal Lossの併用
IBLossは係数で重み付けするだけなので、Focal Lossと併用できます。もともとFocal Lossは不均衡問題を考慮して作られたものです。コードでは次のとおりです。
def ib_focal_loss(input_values, ib, gamma):
"""Computes the ib focal loss"""
p = torch.exp(-input_values)
loss = (1 - p) ** gamma * input_values * ib
return loss.mean()
class IB_FocalLoss(nn.Module):
def __init__(self, weight=None, alpha=10000., gamma=0.):
super(IB_FocalLoss, self).__init__()
assert alpha > 0
self.alpha = alpha
self.epsilon = 0.001
self.weight = weight
self.gamma = gamma
def forward(self, input, target, features):
grads = torch.sum(torch.abs(F.softmax(input, dim=1) - F.one_hot(target, num_classes)),1) # N * 1
ib = grads*(features.reshape(-1))
ib = self.alpha / (ib + self.epsilon)
return ib_focal_loss(F.cross_entropy(input, target, reduction='none', weight=self.weight), ib, self.gamma)
IB weighting factorの部分は全く同じで、最終的な損失の計算が異なるだけです。
実験結果と議論
どこで損失関数を切り替えるか
決定境界が過学習している部分に焦点を当てる以上、通常の訓練方法でロスが大域最小値に到達した段階で切り替えるのが有利です。ただ本論文では、全体の訓練エポックの半分のタイミングで切り替えることを推奨しています。これなら迷う必要がありません。
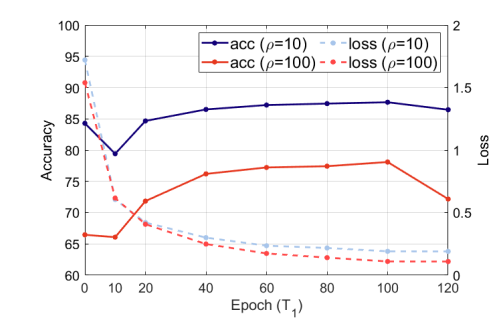
実際に切り替えタイミングを検証したのがこの表で、CIFAR-10で総訓練エポックを200で固定し、CE→IBのロスを切り替えタイミングを変えた(横軸)ものです。ρ=10, 100は不均衡の度合いで、100のほうが強い不均衡を示します。切り替えタイミングに対してはロバストな結果となっていますが、不均衡度に関係なく100エポックで切り替えるのが一番良い結果となりました。「総エポックの半分での切り替えを推奨」という根拠はここにあります。
IB weighting factorを割る時のεが実は重要
式(3)はクロスエントロピーロスをIB weighting factorで割ったものですが、実装上は「符号反転における数値的な不安定性」を避けるために分母に大きい値($\epsilon$)を追加します。実はこの$\epsilon$が精度に少し大き目の変動を与えます。
$$L_{IB}\bigl(y, f(x, w)\bigr)=\frac{L\bigl(y, f(x, w)\bigr)}{\mathcal{IB}(x;w)+\epsilon} \tag{3}$$
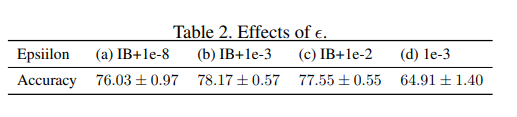
ρ=100のロングテールなCIFAR-10に対して$\epsilon$の値を変えて実験してみましたが、「IB+1e-3」が最も良い結果となりました。IB+1e-8のように小さい値を適用すると2%程度精度が下がります。追加の実験としてIB weighting factorをやめて単に1e-3で割ることをしてみましたが、精度ががくんと落ちています。
なぜ大きめのεが重要かというと、浮動小数点の符号にあります。単なる0除算を避けるためなら1e-8のような小さなεでも良いのです。しかし、浮動小数点数は0に近い値だと数学的には正の数でも、計算上は負の符号を返すことがあるので、それを避けるために1e-3のような少し大きめのεが有効であると考えられます。
実験の詳細
たびたび出てきているロングテールなデータセットは、$k$番目のクラスに対しサンプル数が$n_k\mu^k (mu\in(0, 1))$となるように作っています。不均衡対策として比較しているロスは以下の4つです。
CIFAR-10の場合は、ランダムに初期化されたResNet-32を使い、モメンタムが0.9のSGDを使って200エポック訓練しています。初期学習率は0.1で160エポックと180エポックで0.1倍に減衰させています。最初の5エポックでは線形のウォームアップを使っています。最初の100エポックをクロスエントロピーで学習させ、残りの100エポックはIBロスで訓練させています。「切替時に学習率を調整するのかな」と思ったのですが、特にそこに関しては記述はありませんでした。
Tiny ImageNetではResNet-18を使い、Weight Decay2e-4を入れています。100エポック訓練させ、50エポックでロスを切り替えています。50エポックと90エポックで0.1倍に学習率を減衰させています。
iNaturalist 2018ではResNet-50を学習させました。このケースでは最初の50エポックを普通に学習させ、残りの150エポックをIBロスでファインチューニングしています。学習率は0.01とし、30エポックと180エポックで0.1倍に減衰させています。
CIFAR-10とTiny ImageNetでは1080Tiを1枚、iNaturalist 2018では1080Tiを4枚で訓練させました。
先行研究との比較
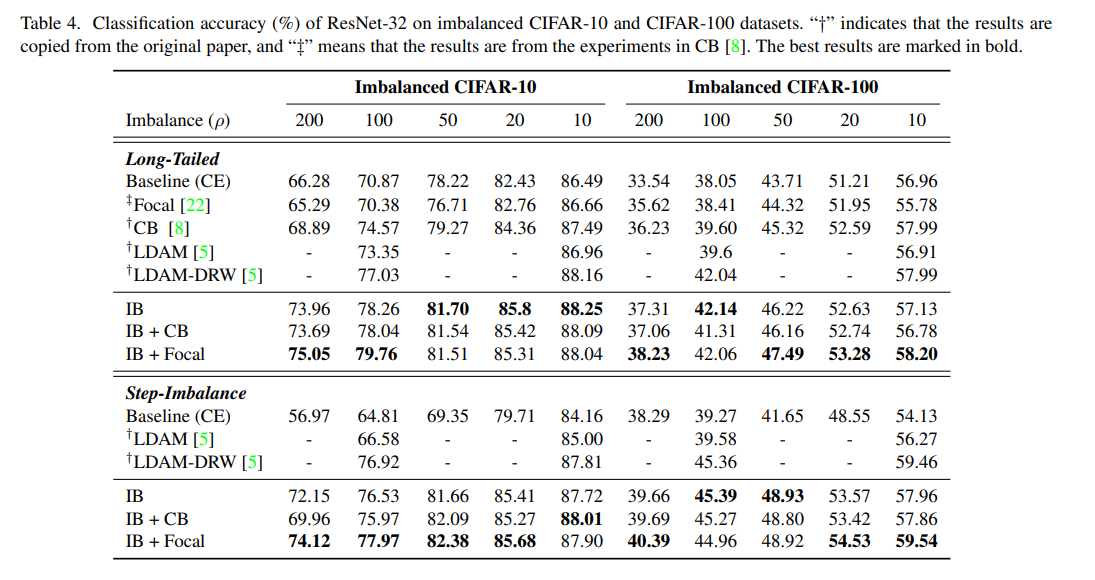
全般的にわかりやすい結果が出ています。IB Lossでのファインチューニングは一貫して有効で、特に不均衡の大きい場合で有効です。例えば、CIFAR-10で不均衡度ρ=200のStep Imbalanceの場合、クロスエントロピーでは(macro)精度が56.97%であったのに対し、IBを入れると72.15%と15%以上引き上げることに成功しました。ロングテールの場合も有効で、単なるFocal LossやCBを単独で使うとクロスエントロピーとあまり変わらないような結果になるのに対し、IBを入れると明らかに良くなっています。
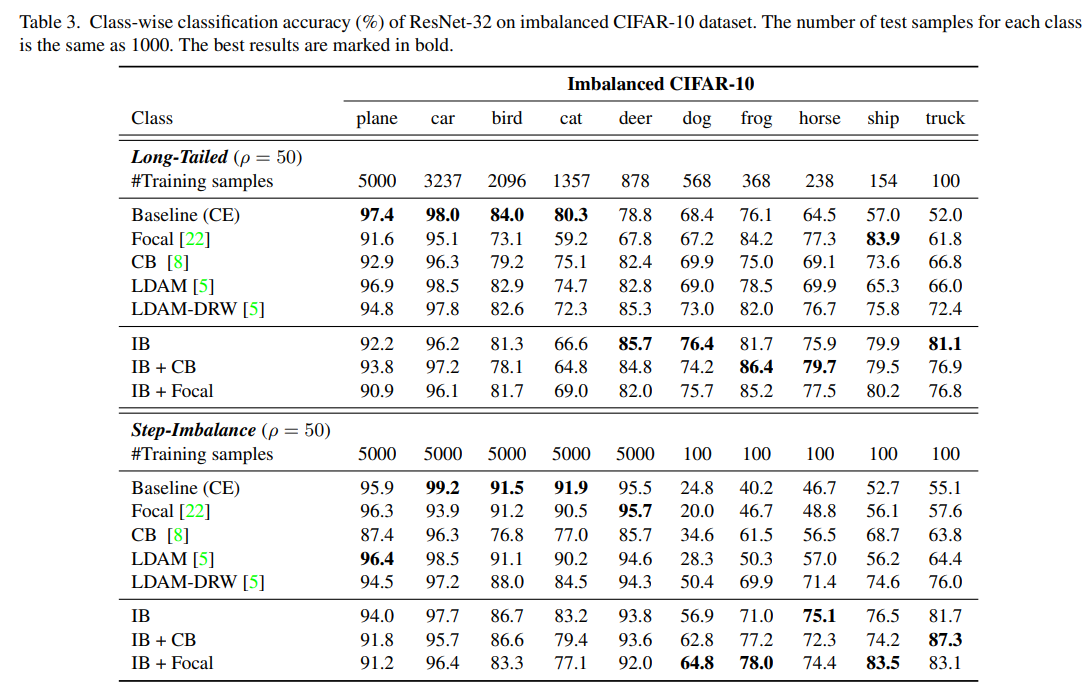
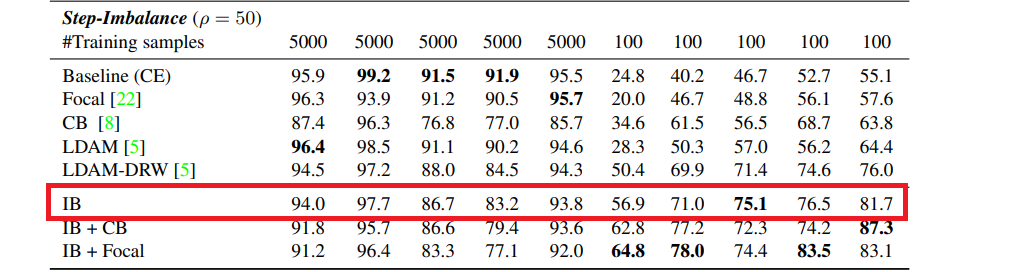
「この表での精度表記がmicroかmacroか?」という点が気になったので確認してみました。例えばStep Imabalaceでρ=50のIBのケースでは精度が81.66%ですが、これを先程のクラス単位の精度表で見ると、
図の赤線で囲った部分に相当します。これらの値を単純平均すると81.66%になるため、先行研究との精度比較(Table 4)で見た値はmacro averageで計算した精度であることがわかります。
また、IBを単独に使うよりもIB+Focalがかなりの例で良いことがわかります。Focal Lossとの併用例は公式コードで用意されているのですぐ使えますね。
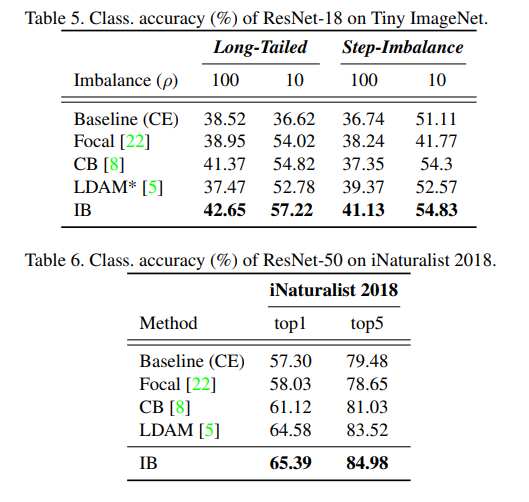
Tiny ImageNetやiNaturalist 2018での結果です。よく「不均衡対策にはFocal Lossが良い、いやいやクロスエントロピーだ」と議論になりますが、IBロスがそれらを軽々と超えてくるぐらいの精度を出せていることがわかります。
まとめと感想
この論文では「不均衡データにおける、決定境界の局所的な過学習とその平滑化」という理論的な側面に着目し、「過学習に寄与している決定境界周辺のサンプルのウェイトを減らす」というシンプルな手法を提唱しました。位置づけとしては「再重み付け」にあたるわけですが、クロスエントロピーで訓練してIBロスでファインチューニングすればいいというシンプルなアプローチが、とても実装的にはやりやすいです。さすがに理論的にちゃんと導出しているだけあって、一貫した良い精度が得られているのは唸らされました。
論文の最後によると「今後はデータレベルやメタ学習ベースの方法を開発し、本手法を拡張していく」ととても意欲的な締め方だったので、今後の研究に期待したいところです。個人的にはこのIB Lossはある意味で「不均衡データに対する決定打の1つ」と捉えることができました。ぜひ使ってみたいところです。
告知
このアドベントカレンダーが本になりました!
https://koshian2.booth.pm/items/3595424
Amazonでも扱いあります詳しくは👉 https://shikoan.com
-
このmicro/macroの概念は他クラス分類のPrecision/Recallの問題で出てきます(Sklearnでも集計方法を指定できます) ↩