前回ニューラルネットワークの協調フィルタリングを使って、種族値を潜在的な特徴量としたレコメンドを考えました。
ニューラルネットワークでおすすめのポケモンを計算してみた
https://qiita.com/koshian2/items/a6c7d37332e8a35cddd8
これは、レーティングを回帰問題として考える教師あり学習のアプローチです。一方でレコメンドのもう1つのアプローチとしてMatrix Fatorizationと呼ばれる方法があります。これは特異値分解といった教師なし学習のアプローチです。今回これを見ていきます。
参考:非負値行列因子分解(NMF)によるレコメンドのちょっとした例
http://smrmkt.hatenablog.jp/entry/2014/08/23/211555
ネットで軽く調べてなんとなく実装できただけなので、理論的なバックグラウンドはかなりあやふやですがご容赦ください。
要点
- scikit-learnで簡単にレコメンド機能を作れる
- 実は主成分分析でもレコメンドは作れる
- PCA,NMFはメリット、デメリットあるから場合によって変えればいい。ついでにNCFもいいぞ。
非負値行列因子分解(Non-negative matrix factorization:NMF)
前回の協調フィルタリングでは、レーティングの行列$Y$、アイテムクロスでの潜在的な特徴量の係数行列を$X$、ユーザークロスでの潜在的な特徴量の係数行列を$\Theta$としたときに、レーティングの推定値$\hat{Y}$を
$$ \hat{Y} = X\Theta^T$$
となるように推定するという問題でした。ただこれ、線形代数のライブラリを使えばなんかできそうな気がしますよね。ちなみにこのYをX、Θの積になるように分割するのを、Matrix Factorization(MF)というそうです。
参考:Matrix Factorizationとは
https://qiita.com/ysekky/items/c81ff24da0390a74fc6c
すごいざっくりとした理解ですが、特異値分解の応用ととらえられます。
参考:潜在的意味インデキシング(LSI)徹底入門
https://abicky.net/2012/03/24/211818/
さて、Non-negative matrix factorization(NMF)はこのMFに、非負の制約を加えたものです。アルゴリズムの内容は割愛しますが、scikit-learnを使えば簡単にできます。普通のMFはなくて、なぜかNMFだけ特別にあるんですよね。
参考:sklearn.decomposition.NMF
http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.NMF.html
実装
前処理としてポケモンの協調フィルタリングのリポジトリからpreprocess.pyを実行して、data.npzがあるものとします。まずは前回と同様に未評価の項目を再現するためにマスクを導入します。
import numpy as np
from sklearn.decomposition import NMF
# データの読み込み
pokemon = np.load("data.npz")
# 定数
n_pokemon, n_trainer = pokemon["data"].shape #(151, 25)
# より実践的な例にするために未評価の項目を入れる
np.random.seed(151)
rand = np.random.uniform(size=(n_pokemon, n_trainer))
# 乱数が0.6以下なら未評価とする
mask = (rand > 0.6).astype(int)
data = pokemon["data"]
data[mask==0] = 0
コード全体:https://gist.github.com/koshian2/bf2cb951a921ddd65aa2c01046ba5195
NMFはscikit-learnを使えば一瞬でできます。
nmf = NMF(n_components=5, random_state=151)
W = nmf.fit_transform(data) # アイテムクロスの特徴量
H = nmf.components_ # ユーザークロスの特徴量
print(W.shape) # (151, 5)
print(H.shape) # (5, 25)
predict = np.dot(W, H)
ちなみにWがポケモン単位の特徴量($=X$)、Hがトレーナー単位の特徴量($=\Theta^T$)となります。推定値はこの2つの内積を取ればいいだけです。
計算もほんの1,2秒で、同じデータでニューラルネットワークが2分ぐらい訓練に要した(fit_generatorで2重のforループを行っていたので、これを取ればもう少し高速化はできます)のと比べると全然速いです。ただし、この速さは計算量のオーダーに基づいたものではなく、たまたまこのデータに対してそうだったからで、データのサイズが変わっても同じかと言われるとそうは言いきれません。
さてレコメンドの結果をみてみましょう。
# おすすめのポケモンを上位10件表示
def recommendation_view(pred, mask):
global pokemon
# 評価済みポケモン
print("評価済みポケモン")
print(pokemon["pokemon_names"][mask==1])
# 予測レート
score = pred * (1-mask)
# ポケモンのインデックス
index = np.argsort(score)[::-1][:10]
cnt = 1
print("おすすめのポケモン一覧")
for i in index:
if mask[i] == 1: break
print(cnt, "位 : id =", i+1, "(", pokemon["pokemon_names"][i], ")", "予測レート :", score[i])
cnt += 1
print()
# 攻撃極振りが好きなトレーナー2の場合
print("★NMF★")
print("-攻撃極振りのトレーナー2の場合")
recommendation_view(predict[:,1], mask[:,1])
print()
# 防御極振りが好きなトレーナー3の場合
print("-防御極振りのトレーナー3の場合")
recommendation_view(predict[:,2], mask[:,2])
print()
-攻撃極振りのトレーナー2の場合
評価済みポケモン
['フシギソウ' 'ヒトカゲ' 'リザード' 'リザードン' 'ゼニガメ' 'カメックス'
(中略)
'シャワーズ' 'ポリゴン' 'オムナイト' 'カブト' 'サンダー' 'ハクリュー' 'ミュウ']
おすすめのポケモン一覧
1 位 : id = 150 ( ミュウツー ) 予測レート : 2.9441955028569313
2 位 : id = 135 ( サンダース ) 予測レート : 2.4622273891934645
3 位 : id = 142 ( プテラ ) 予測レート : 2.4299797024215946
4 位 : id = 91 ( パルシェン ) 予測レート : 2.063317793750097
5 位 : id = 78 ( ギャロップ ) 予測レート : 2.034039662314253
6 位 : id = 17 ( ピジョン ) 予測レート : 1.9938962712718153
7 位 : id = 34 ( ニドキング ) 予測レート : 1.9617608012857377
8 位 : id = 45 ( ラフレシア ) 予測レート : 1.839128223502845
9 位 : id = 62 ( ニョロボン ) 予測レート : 1.719322618143872
10 位 : id = 121 ( スターミー ) 予測レート : 1.7148362686165994
-防御極振りのトレーナー3の場合
評価済みポケモン
['フシギソウ' 'キャタピー' 'バタフリー' 'スピアー' 'ポッポ' 'ピジョット'
(中略)
'ミュウツー' 'ミュウ']
おすすめのポケモン一覧
1 位 : id = 55 ( ゴルダック ) 予測レート : 1.9126134587280517
2 位 : id = 73 ( ドククラゲ ) 予測レート : 1.8473437483090949
3 位 : id = 143 ( カビゴン ) 予測レート : 1.710399821495604
4 位 : id = 110 ( マタドガス ) 予測レート : 1.6623222936956081
5 位 : id = 105 ( ガラガラ ) 予測レート : 1.6359807497106864
6 位 : id = 51 ( ダグトリオ ) 予測レート : 1.6066801107145432
7 位 : id = 42 ( ゴルバット ) 予測レート : 1.595747148028717
8 位 : id = 145 ( サンダー ) 予測レート : 1.5232421841809487
9 位 : id = 65 ( フーディン ) 予測レート : 1.4426721473897035
10 位 : id = 9 ( カメックス ) 予測レート : 1.441481696774678
順位はまだしもあれ、全般的にレーティング低くないですか?多分これ、未評価の項目が計算に使われてしまって、行列がスパースになればなるほど予測レートが下がっていくのだと思います。なので、このままだと順位は信用できても、出てきた予測レートはほとんど信用できません。
さて、前回の協調フィルタリングでは、事前にアイテム単位の平均で予測値を引いておくというテクニックを使いました。もともとこれは何もレーティングしていないユーザーに対して平均値を返すテクニックですが、予測レートが下がってしまう影響を緩和する効果もあります。ただし、NMFの場合はNMFの非負の制約が逆に悪さをして平均シフトができません(平均シフトをするとマイナスになるから)。
まとめ
- アイテムベース、ユーザーベースの係数は全て正になる。解析上この制約がほしい場合は有効
- レコメンドとして用いる場合は、レコメンドの順位は信頼できるが、推定値は信用できない。なぜなら目的関数にデータのスパース性を考慮していないから。
- 平均シフトはNMFの非負条件によりできない
主成分分析(PCA)による平均シフト
さて、アルゴリズムとしてはだいぶ後退しますが、MFが特異値分解を使っていたのなら、同じ特異値分解を使っている主成分分析(PCA)を使ってもいけるんじゃね?と思いました。PCAと特異値分解(SVD)には密接な関係があり、詳しくは以下の記事を見てください。
参考:PCAとSVDの関連について
https://qiita.com/horiem/items/71380db4b659fb9307b4
PCAの場合は非負の制約がないので平均シフトができます。しかもPCAはscikit-learnで同様にできます。(普通のMFをやりたければPCAを使えということでしょうか)
実装
データのマスキングの部分他NMFとダブる部分は省略します。アイテム単位での平均値を計算し、データからシフトさせます。
# ポケモンごとの平均値を計算
avg = np.zeros(n_pokemon)
for i in range(n_pokemon):
slice = data[i, mask[i, :]==1]
if(len(slice) > 0):
avg[i] = np.mean(slice)
# 観測値から平均値を引く
data = (data - np.tile(avg, (n_trainer, 1)).T) * mask
コード全体:https://gist.github.com/koshian2/c2b15752111bc1a2de315db6f8573525
次に主成分分析をします。NMFのときと同様です。
from sklearn.decomposition import PCA
model = PCA(n_components=5, random_state=151)
W = model.fit_transform(data) # アイテムクロス
H = model.components_ # ユーザークロス
print(W.shape) # (151, 5)
print(H.shape) # (5, 25)
predict = np.dot(W, H)
速度はNMFとほぼ変わりません。最後にシフトした平均を推定値に戻します。
# 平均をプラスする
predict = predict + np.tile(avg, (n_trainer, 1)).T
レコメンド結果を見てみましょう。
-攻撃極振りのトレーナー2の場合
おすすめのポケモン一覧
1 位 : id = 150 ( ミュウツー ) 予測レート : 4.538914571013628
2 位 : id = 130 ( ギャラドス ) 予測レート : 4.217439424326646
3 位 : id = 91 ( パルシェン ) 予測レート : 4.177447096654304
4 位 : id = 85 ( ドードリオ ) 予測レート : 4.147032968918887
5 位 : id = 135 ( サンダース ) 予測レート : 4.057463448430615
6 位 : id = 142 ( プテラ ) 予測レート : 4.022549488574631
7 位 : id = 112 ( サイドン ) 予測レート : 3.9693568808032187
8 位 : id = 141 ( カブトプス ) 予測レート : 3.9137524240454766
9 位 : id = 136 ( ブースター ) 予測レート : 3.8854951917365725
10 位 : id = 103 ( ナッシー ) 予測レート : 3.882288841794628
-防御極振りのトレーナー3の場合
おすすめのポケモン一覧
1 位 : id = 85 ( ドードリオ ) 予測レート : 4.444969437565834
2 位 : id = 130 ( ギャラドス ) 予測レート : 4.360686371512144
3 位 : id = 68 ( カイリキー ) 予測レート : 4.265535478066673
4 位 : id = 65 ( フーディン ) 予測レート : 4.23471968561494
5 位 : id = 59 ( ウインディ ) 予測レート : 4.187944379808223
6 位 : id = 3 ( フシギバナ ) 予測レート : 4.140023459762753
7 位 : id = 149 ( カイリュー ) 予測レート : 4.131011612418561
8 位 : id = 103 ( ナッシー ) 予測レート : 4.131011612418561
9 位 : id = 145 ( サンダー ) 予測レート : 4.131011612418561
10 位 : id = 135 ( サンダース ) 予測レート : 4.127262329660678
確かにレーティングは信用できますが、結果はどうでしょうか。攻撃極振りの場合はまだしも、防御極振りのトレーナーに対しておすすめされているポケモンは、必ずしも防御が高いとはいえません。
ちなみに主成分分析の場合、そのまま分散比が取れるので潜在的な特徴量の数を見たい場合は便利そうです。
print(np.sum(model.explained_variance_ratio_))
# 0.508967784318267
本来の潜在特徴量は5個なのに(なぜなら種族値をベースに人工データを作り、種族値が5個だから)、5個だと半分ぐらいしか分散が残っていないんですね。確かにこれだとちょっとうーんという感じはします。それを実感するために、係数行列をもとにアイテム間の類似度を計算してみます
ポケモン間の類似度
これはNMFでもできますが、求められたアイテム単位の係数行列をもとにコサイン類似度を計算して、「あるポケモンに似たポケモン」を計算してみます。
from sklearn.metrics.pairwise import cosine_similarity
# コサイン類似度
def print_similar(data, index):
global pokemon
cosine = cosine_similarity(data[index, :].reshape(1, -1), data)
# 類似度トップ10
similar_indices = np.argsort(np.ravel(cosine))[::-1][1:10]
cnt = 1
print("--", pokemon["pokemon_names"][index], "と似ているポケモン --")
for idx in similar_indices:
print("第", cnt, "位 :", pokemon["pokemon_names"][idx], "(id =", idx+1, ")", "類似度 =", cosine[0, idx])
cnt += 1
print()
print_similar(predict, 0)
print_similar(predict, 24)
-- フシギダネ と似ているポケモン --
第 1 位 : クサイハナ (id = 44 ) 類似度 = 0.9999205512236674
第 2 位 : マダツボミ (id = 69 ) 類似度 = 0.9998459688008584
第 3 位 : ベトベター (id = 88 ) 類似度 = 0.9993112227428961
第 4 位 : メタモン (id = 132 ) 類似度 = 0.9992834724878206
第 5 位 : カメール (id = 8 ) 類似度 = 0.9991140686603192
第 6 位 : リザード (id = 5 ) 類似度 = 0.9991064250240955
第 7 位 : イーブイ (id = 133 ) 類似度 = 0.998892599538796
第 8 位 : オムナイト (id = 138 ) 類似度 = 0.9988421017511405
第 9 位 : キングラー (id = 99 ) 類似度 = 0.9988184925518775
-- ピカチュウ と似ているポケモン --
第 1 位 : トサキント (id = 118 ) 類似度 = 0.9999652736976531
第 2 位 : ウインディ (id = 59 ) 類似度 = 0.9998966781620228
第 3 位 : フシギバナ (id = 3 ) 類似度 = 0.9998695121458085
第 4 位 : サンダース (id = 135 ) 類似度 = 0.9997948906994282
第 5 位 : ウツボット (id = 71 ) 類似度 = 0.9995701004884253
第 6 位 : ズバット (id = 41 ) 類似度 = 0.9995268781748127
第 7 位 : ロコン (id = 37 ) 類似度 = 0.9995260898185343
第 8 位 : ドードリオ (id = 85 ) 類似度 = 0.9993380496041716
第 9 位 : ゴルバット (id = 42 ) 類似度 = 0.999223428181614
類似度的にはかなり密集していて”潰れている”印象を受けます。ちなみに、本来の種族値から計算したコサイン類似度は次のようになります。種族値は各パラメーターの最大値で標準化済みです(詳細は前の記事を読んでください)。
print("★種族値ベース★")
print_similar(pokemon["pokemon_spicies"], 0)
print_similar(pokemon["pokemon_spicies"], 24)
★種族値ベース★
-- フシギダネ と似ているポケモン --
第 1 位 : フシギソウ (id = 2 ) 類似度 = 0.9995097398292925
第 2 位 : ファイヤー (id = 146 ) 類似度 = 0.9993877489608776
第 3 位 : フリーザー (id = 144 ) 類似度 = 0.998527416573452
第 4 位 : フシギバナ (id = 3 ) 類似度 = 0.998391972844298
第 5 位 : サンダー (id = 145 ) 類似度 = 0.9967137443195917
第 6 位 : イーブイ (id = 133 ) 類似度 = 0.9965519163886356
第 7 位 : ジュゴン (id = 87 ) 類似度 = 0.9958404131363452
第 8 位 : スリーパー (id = 97 ) 類似度 = 0.9952182344780379
第 9 位 : パウワウ (id = 86 ) 類似度 = 0.9930073389640012
-- ピカチュウ と似ているポケモン --
第 1 位 : ダグトリオ (id = 51 ) 類似度 = 0.9974983391173142
第 2 位 : ニョロモ (id = 60 ) 類似度 = 0.9940184498185707
第 3 位 : ニャース (id = 52 ) 類似度 = 0.9936720584963512
第 4 位 : ペルシアン (id = 53 ) 類似度 = 0.9924397840970327
第 5 位 : ディグダ (id = 50 ) 類似度 = 0.9910860283430455
第 6 位 : エレブー (id = 125 ) 類似度 = 0.9842717791298208
第 7 位 : プテラ (id = 142 ) 類似度 = 0.9836826994325448
第 8 位 : オニスズメ (id = 21 ) 類似度 = 0.981648153427737
第 9 位 : ヒトカゲ (id = 4 ) 類似度 = 0.9803897164054607
本来の類似度よりも、類似度の値がかなり潰れている(ポケモン間の差が縮んでいる)印象を受けます。次元を圧縮して分散が落ちた影響だと思います。
NMFでのポケモンの類似度
同様にNMFの場合も見てみます。
-- フシギダネ と似ているポケモン --
第 1 位 : マルマイン (id = 101 ) 類似度 = 0.9968511052738767
第 2 位 : ワンリキー (id = 66 ) 類似度 = 0.9880588192794733
第 3 位 : オニドリル (id = 22 ) 類似度 = 0.9809883903570601
第 4 位 : ガーディ (id = 58 ) 類似度 = 0.9802873435240976
第 5 位 : ベトベター (id = 88 ) 類似度 = 0.9778518410986304
第 6 位 : ニョロゾ (id = 61 ) 類似度 = 0.9729248430341464
第 7 位 : ゴルダック (id = 55 ) 類似度 = 0.9646739441688635
第 8 位 : カメール (id = 8 ) 類似度 = 0.9625921889450768
第 9 位 : ドードリオ (id = 85 ) 類似度 = 0.9612832365391807
-- ピカチュウ と似ているポケモン --
第 1 位 : パウワウ (id = 86 ) 類似度 = 0.9828320159181755
第 2 位 : ニドラン♂ (id = 32 ) 類似度 = 0.9711957955393349
第 3 位 : サワムラー (id = 106 ) 類似度 = 0.9682693767248864
第 4 位 : レアコイル (id = 82 ) 類似度 = 0.9672502892575552
第 5 位 : ピジョン (id = 17 ) 類似度 = 0.9672212832686565
第 6 位 : アーボック (id = 24 ) 類似度 = 0.9612160247105203
第 7 位 : アーボ (id = 23 ) 類似度 = 0.9561910048073112
第 8 位 : サンドパン (id = 28 ) 類似度 = 0.9548703534551223
第 9 位 : スリーパー (id = 97 ) 類似度 = 0.9515858165032728
フシギダネとマルマインが似てるってちょっと直感的ではないような。
NCFでのポケモンの類似度
参考までに前回のニューラルネットワークでの協調フィルタリング(NCF)での推定値(中間層の結果を取っています。中間層での活性化関数はrelu→tanhにしました)は以下の通りです。
-- フシギダネ と似ているポケモン --
第 1 位 : マダツボミ (id = 69 ) 類似度 = 0.93753713
第 2 位 : ゴルダック (id = 55 ) 類似度 = 0.93059546
第 3 位 : レアコイル (id = 82 ) 類似度 = 0.92993754
第 4 位 : シードラ (id = 117 ) 類似度 = 0.9149238
第 5 位 : カメール (id = 8 ) 類似度 = 0.9004642
第 6 位 : オムナイト (id = 138 ) 類似度 = 0.8977397
第 7 位 : アズマオウ (id = 119 ) 類似度 = 0.8852239
第 8 位 : リザード (id = 5 ) 類似度 = 0.88403285
第 9 位 : カラカラ (id = 104 ) 類似度 = 0.86258614
-- ピカチュウ と似ているポケモン --
第 1 位 : トサキント (id = 118 ) 類似度 = 0.9907586
第 2 位 : ウインディ (id = 59 ) 類似度 = 0.98211044
第 3 位 : フシギバナ (id = 3 ) 類似度 = 0.97478056
第 4 位 : ピジョン (id = 17 ) 類似度 = 0.9710602
第 5 位 : アーボ (id = 23 ) 類似度 = 0.9691885
第 6 位 : ドードリオ (id = 85 ) 類似度 = 0.95489216
第 7 位 : コダック (id = 54 ) 類似度 = 0.9533706
第 8 位 : プテラ (id = 142 ) 類似度 = 0.9414476
第 9 位 : ラッタ (id = 20 ) 類似度 = 0.92875445
ピカチュウの上位3体がPCAと同じですね。ニューラルネットワークを使うと結果的に主成分分析を表現できるとも言えるでしょう。類似度の差がかえって広がっているのが面白い。
ポケモンの特徴量をアルゴリズム別にプロットしてみる
ポケモンの類似度を見てもイマイチピンとこないので、アルゴリズムごとに求められた、ポケモン単位での係数行列を主成分分析して2次元に落とします。ここでの主成分分析はプロット用でそれ以上の意味はありません。
import matplotlib.pyplot as plt
plot_W = PCA(n_components=2).fit_transform(W)
plt.plot(plot_W[:, 0], plot_W[:, 1], ".")
plt.title("PCA")
plt.show()
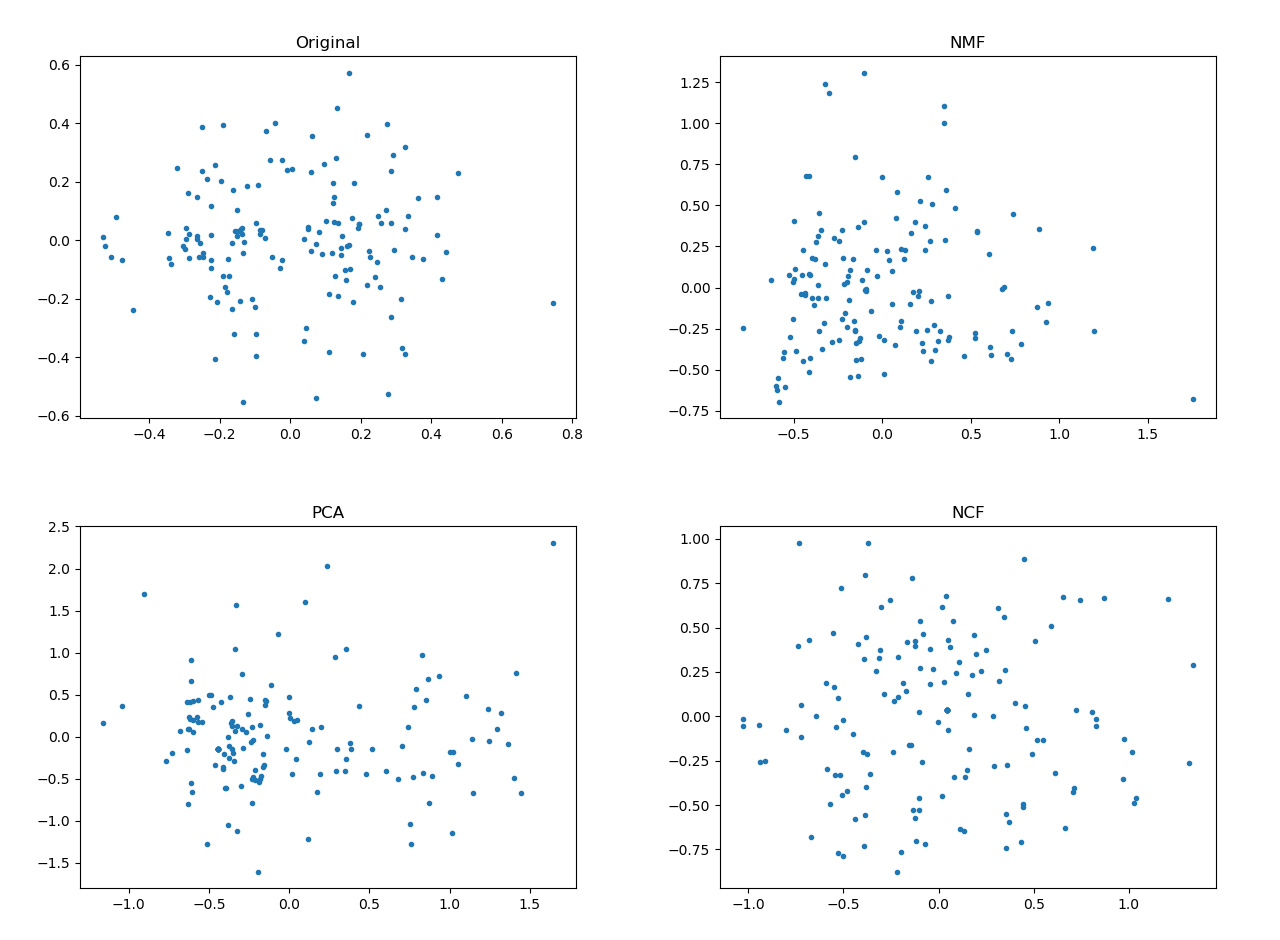
上からオリジナル(種族値を2次元に投射)、NMFの場合、PCA、NCFの場合です。もともと種族値が均一分布ではないので、オリジナルデータがかなりムラがあるプロットになっています。PCAの場合はあまり変わらない、NMFはかなり歪んで左下にシフトしました。PCAは普通に次元落としただけなのでそれに見合った感じですが、NMFは非負制約と歪みのトレードオフ感は否めません。一方でNCFの場合は活性化関数にtanhを入れたせいか、オリジナルよりも拡散しています。これをいいととるか悪いととるかは評価は分かれそうです。
PCAまとめ
- 主成分分析の行列分解を用いてレコメンドシステムを構築できる
- アイテム単位の平均シフトを使えば、レーティングがないユーザーに対してそのアイテムの平均値を提供することができる。PCAもスパース性を考慮していないが、平均を加えることでその影響が多少和らぐ。結果的にレーティングの推定値も納得しやすいものとなっている。
- 非負制約と引き換えにNMFよりも係数の分布がオリジナルに近いものになっている
- PCAがいいかNMFがいいかは議論の余地がある(何らかの評価尺度が必要)が、係数の非負制約が必要かどうかが1つの重要なポイント
ニューラルネットワークと比較して
前回のニューラルネットワークと比べて今回のはかなり古典的な手法でしたが、どちらがいいの?と言われて自分なりの感想を書いておきます。
- PCA/NMFのメリット→速いし簡単。ただ、行列の特異値分解も速いアルゴリズムではなく(古典的なアルゴリズムだと$O(N^3)$)、PCA/NMFとNCFを共通の尺度で比較できないので、データのサイズ次第ではNCFとどっちが速いかはよくわからない。でも多分PCA/NMFのほうが速い。
- NCFのメリット→モデルの拡張が簡単で非線形の特徴量抽出をガンガン入れられる。計算資源が許せば精度面ではNCFのほうが伸びしろが大きい。前回の論文ではNCFのほうが良いと述べられていた。あと、未評価の項目の欠損値をカスタムの損失関数として簡単に定義できる。
なので、データ量と計算量の兼ね合いでどっちもやってみればいいんじゃないかなと思いました。個人的にはニューラルネットワークでPCAを表現できたのが面白いなと思いました。