PCA, Kernel-PCA, t-SNE, CNNによる可視化のための次元削減の比較 #Python

画像の特徴量を可視化のために、2次元への次元削減を考えます。次元削減の結果を主成分分析（PCA）、カーネルあり主成分分析（Kernel-PCA）、t-SNE、畳込みニューラルネットワーク（CNN）で比較します。

最後のCNN以外は比較的よくある方法だと思います。CNNをデータの可視化のために使うというのはあまり一般的ではありませんが、AutoEncoderの真ん中の特徴量を取ってプロットするという方法はとても強力な方法なので（例、他にも「AutoEncoder 可視化」で検索するとよく出てきます）、それの簡易版という位置づけです。AutoEncoderの場合、アップサンプリング方面も含めて、分類器としてのCNNの倍のレイヤーが必要になるので、分類器の隠れ層の値を拝借したほうが計算的に楽できるだろうなと思って実装してみたらそこそこいい感じになりました。

ちなみにt-SNEはScikit-learnで行ったのですが、Kerasでのニューラルネットワークを用いた（Parametric）t-SNEの実装もあります。コードを読んでいると、通常のニューラルネットワークでXをPという値に変換してこれをYとし、KLダイバージェンスを評価尺度として訓練させているので、t-SNEもAutoEncoderもこのCNNの隠れ層も用いた例も、「全てニューラルネットワークの設定を少し変えただけで定義できるのでは？」とざっくりと理解しました。

順に見ていきましょう（理論的にガバガバなのは勘弁してね！）。

可視化用のデータローダー

まずは可視化用のデータローダーを定義しておきます。

dataloader.py

import numpy as np
from keras.datasets import mnist

def load_visualize_data(n_sample):
    (_, _), (X_test, y_test) = mnist.load_data()
    X = np.zeros((n_sample * 10, X_test.shape[1], X_test.shape[2]))
    y = np.zeros(n_sample*10)
    for num in range(10):
        dest_indices = np.arange(num*n_sample, (num+1)*n_sample)
        source_indices = np.where(y_test == num)[0][:n_sample]
        X[dest_indices, :, :] = X_test[source_indices, :, :]
        y[dest_indices] = y_test[source_indices]
    return X, y

KerasのMNISTのテストデータから、0～9の各ラベルに対して、n_sample(100)個、n_sample=100の場合は1000個サンプルを取り出して並べただけです。各アルゴリズムでプロットするデータは全てこれを用います。

(1)PCA（主成分分析）

まずはおなじみの主成分分析。Scikit-learnで一発です。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.cm import get_cmap
from sklearn.decomposition import PCA
from sklearn.metrics import explained_variance_score
from dataloader import load_visualize_data

X, y = load_visualize_data(100)
X /= 255
X = X.reshape(X.shape[0], -1)

decomp = PCA(n_components=2)
X_decomp = decomp.fit_transform(X)

# 分散比の計算
evs = explained_variance_score(X, decomp.inverse_transform(X_decomp))

cmap = get_cmap("tab10")
for i in range(10):
    marker = "$" + str(i) + "$"
    indices = np.arange(i*100, (i+1)*100)
    plt.scatter(X_decomp[indices, 0], X_decomp[indices, 1], marker=marker, color=cmap(i))
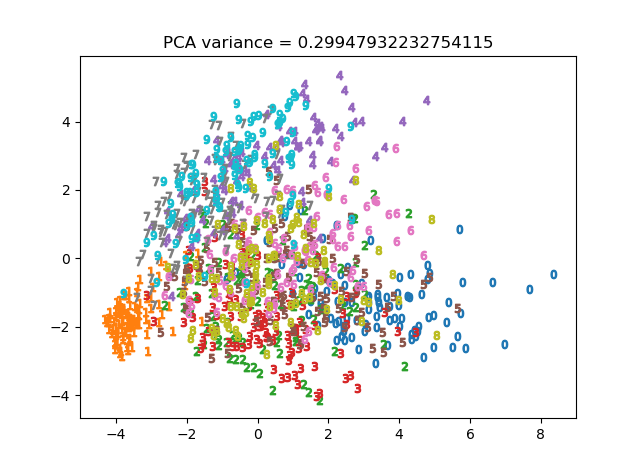
plt.title(f"PCA variance = {evs}")
plt.show()

PCAにはexplained_variance_ratio_という変数があり、これで元のデータとの分散比の比較ができますが、後ほどのKernelPCAでは特徴量の空間が変わってしまうため、共通の尺度として利用できなくなってしまいます。逆変換してexplained_variance_scoreで比較しました。

可もなく不可もなくという感じです。

(2) Kernel-PCA

次にKernel-PCAで次元削減をしてみます。理論的なことはこちらが詳しいです。

今回はガウス（RBF）カーネルを使います。サポートベクターマシンのRBFカーネルと同様に、γというハイパーパラメータがあります。今回explained_variance_scoreが大きくなるようにγを設定しました（γ＝10^9）。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.cm import get_cmap
from sklearn.decomposition import KernelPCA
from sklearn.metrics import explained_variance_score
from dataloader import load_visualize_data

X, y = load_visualize_data(100)
X /= 255
X = X.reshape(X.shape[0], -1)

decomp = KernelPCA(n_components=2, kernel="rbf", gamma=1e9, fit_inverse_transform=True)
X_decomp = decomp.fit_transform(X)

# 分散比の計算
evs = explained_variance_score(X, decomp.inverse_transform(X_decomp))
print(evs)

cmap = get_cmap("tab10")
for i in range(10):
    marker = "$" + str(i) + "$"
    indices = np.arange(i*100, (i+1)*100)
    plt.scatter(X_decomp[indices, 0], X_decomp[indices, 1], marker=marker, color=cmap(i))
plt.xlim((-0.15, 0.1))
plt.ylim((-0.15, 0.15))
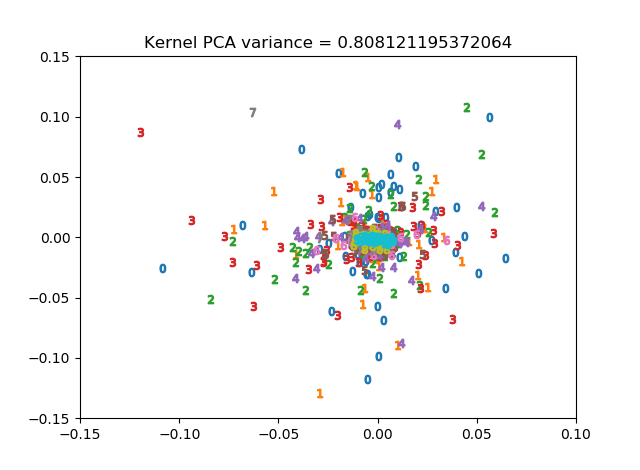
plt.title(f"Kernel PCA variance = {evs}")
plt.show()

explained_variance_scoreは高かったものの、密集してしまっていまいち？

(3)t-SNE

2次元や3次元の次元削減限定として、t-SNEというとても良いアルゴリズムがあります。理論的なことはこちらが詳しいです。これも同様にScikit-learnでできます。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.cm import get_cmap
from sklearn.manifold import TSNE
from sklearn.metrics import explained_variance_score
from dataloader import load_visualize_data

X, y = load_visualize_data(100)
X /= 255
X = X.reshape(X.shape[0], -1)

decomp = TSNE(n_components=2)
X_decomp = decomp.fit_transform(X)

cmap = get_cmap("tab10")
for i in range(10):
    marker = "$" + str(i) + "$"
    indices = np.arange(i*100, (i+1)*100)
    plt.scatter(X_decomp[indices, 0], X_decomp[indices, 1], marker=marker, color=cmap(i))
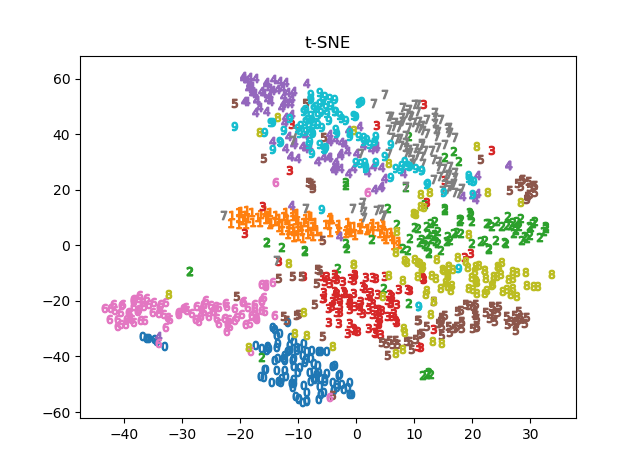
plt.title(f"t-SNE")
plt.show()

かなりきれいに出てきます。今までの中で一番綺麗に出てきます。計算も1分もかかりません。

ただしうまくいくのは3次元までのようです。例えば、n_componentsに4を代入すると、

出力

    raise ValueError("'n_components' should be inferior to 4 for the "
ValueError: 'n_components' should be inferior to 4 for the barnes_hut algorithm
as it relies on quad-tree or oct-tree.

デフォルトのbarnes_hutアルゴリズムは4次元以上で使えないから別のアルゴリズムを使いなさいと、怒られます。Scikit-learnのページによると、3次元以下しか使えないbarnes_hutでは$O(N\log N)$の計算量でできるが、4次元以上でも使えるexactアルゴリズムは$O(N^2)$の計算量が必要とのこと。

Nというのがデータ数なのか次元数なのかわかりませんでしたが、t-SNEのexactアルゴリズムでMovie-Lens 1Mを256次元に削減しようとしたところ半日経っても答えが出てこなかったので、計算量だけは注意してください。MNISTでもexactの256次元はexactの2次元より明らかに時間かかります。場合によってはニューラルネットワークのアプローチのほうが多分速いと思います。

Scikit-learnのt-SNEではinverse_transformの変換がないので、Kernel-PCAのような分散比の比較はできませんでした。分散比を比較のようなことをやりたいのならやはりAutoEncoderのような実装をすべきなのかなーと。

(4) CNNの隠れ層の値を取る

もともと「CNNの出力層に近い隠れ層をtanhで定義して、その値を取り出せばKernel-PCAみたいな次元削減できるよね」というのがもともとの発想だったのでそれを実装します。MNISTでCNNを使うのはオーバーキル感がありますが、以下のようなCNNを定義しました。

import numpy as np
import os
import pickle
import matplotlib.pyplot as plt
from matplotlib.cm import get_cmap
from keras.layers import Input, Conv2D, Activation, BatchNormalization, MaxPool2D, Flatten, Dense
from keras.models import Model
from keras.datasets import mnist
from keras.optimizers import Adam
from keras.callbacks import Callback
from keras.utils import to_categorical
from dataloader import load_visualize_data

(X_train, y_train), (_, _) = mnist.load_data()
X_train = X_train / 255.0
X_train = X_train[:, :, :, np.newaxis]
y_train = to_categorical(y_train, num_classes=10)

input = Input(shape=(28, 28, 1))
X = Conv2D(8, kernel_size=(3,3))(input)
X = MaxPool2D((2,2))(X)
X = BatchNormalization()(X)
X = Activation("relu")(X)#13
X = Conv2D(16, kernel_size=(2,2))(X)
X = MaxPool2D((2,2))(X)
X = BatchNormalization()(X)
X = Activation("relu")(X)#6
X = Conv2D(32, kernel_size=(2,2))(X)
X = Conv2D(32, kernel_size=(2,2))(X)
X = BatchNormalization()(X)
X = Activation("relu")(X) #4
X = Flatten()(X)
X = Dense(32)(X)
X = Activation("relu")(X)
X = Dense(2)(X)
X = BatchNormalization()(X)
X = Activation("tanh", name="latent-features")(X)
output = Dense(10, activation="softmax")(X)

model = Model(inputs=input, outputs=output)
model.compile(optimizer=Adam(lr=0.01), loss="categorical_crossentropy", metrics=["accuracy"])

浅めのCNNですが、ReLUとBatchNormを使った今風なモデルです。ここでのポイントは、softmaxの出力層の前の隠れ層を2ユニットにして、活性化関数にtanhを使っていることです。つまり、分類問題として訓練して、あとでtanhの層を取り出せば、MNISTの一般的な可視化用の次元削減器ができるというわけです。AutoEncoderの場合は、入力層と出力層が同じ画像になるように訓練して中間層を取り出しますが、それの簡易版という感じです。

100epoch訓練させて、訓練精度は99.7%となりました。CPUで1分/epoch、Google ColabのGPU使って訓練させたら10秒/epochぐらいだったので、計算コストは全然軽いです。プロットは次のようにします。

X_plot, y_plot = load_visualize_data(100)
X_plot = X_plot / 255.0
X_plot = X_plot[:, :, :, np.newaxis]
cmap = get_cmap("tab10")

class MyCallback(Callback):
    def on_epoch_end(self, epoch, logs={}):
        # モデルの保存
        if not os.path.exists("model"): os.mkdir("model")
        model.save(f"model/epoch_{epoch:03d}.h5")
        # プロット
        latent = Model(inputs=model.input, outputs=model.get_layer("latent-features").output)
        pred = latent.predict(X_plot)
        plt.figure()
        for j in range(10):
            marker = "$" + str(j) + "$"
            indices = np.arange(j*100, (j+1)*100)
            plt.scatter(pred[indices, 0], pred[indices, 1], marker=marker, color=cmap(j))
        plt.title(f"CNN epoch = {epoch} / train acc = {logs['acc']:04f}")
        # 画像を保存
        if not os.path.exists("images"): os.mkdir("images")
        plt.savefig(f"images/epoch{epoch:03d}.png")

history = model.fit(X_train, y_train, batch_size=128, epochs=100, callbacks=[MyCallback()]).history
with open("model/history.dat", "wb") as fp:
    pickle.dump(history, fp)

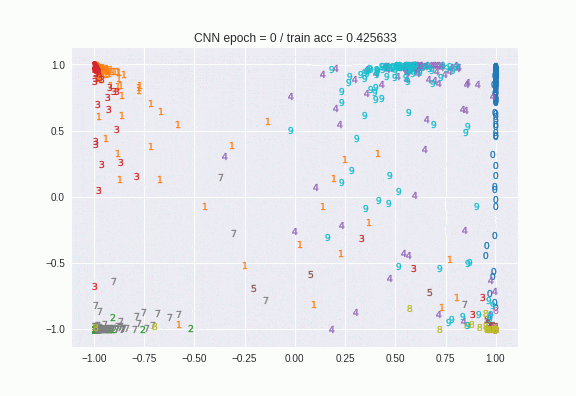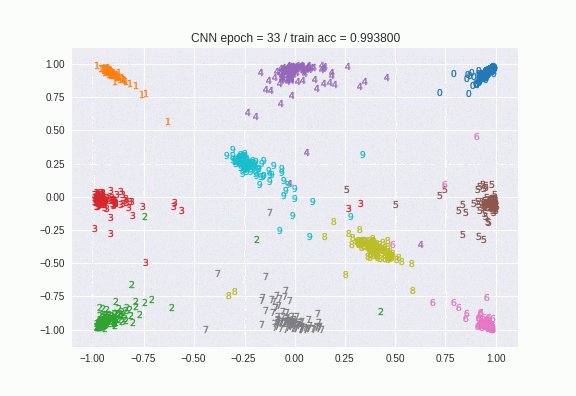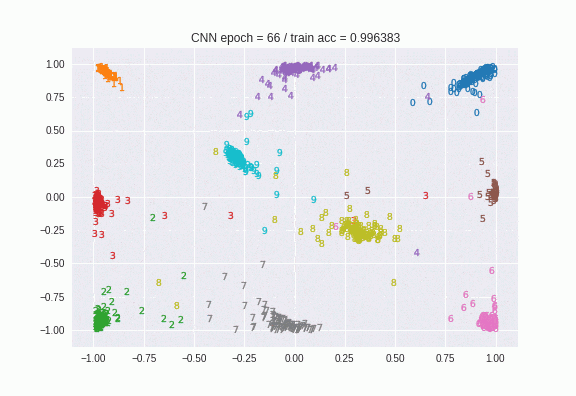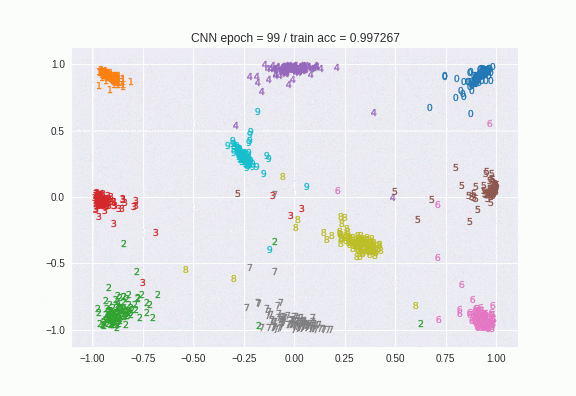
epochの終わりで呼ばれるコールバックで定義しました。modelの出力層を1つ前の「latent-features」という名前のtanhの層に変えたモデルをlatentとします。そのlatentというモデルに対してpredictをすると中間層の値が得られるというわけです。それをプロットしたものがこちらです。

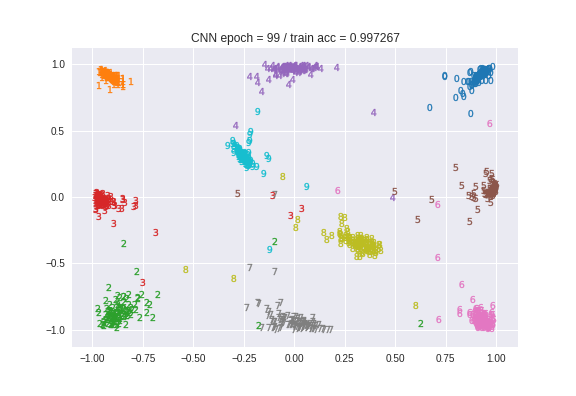
はじめはバラバラだったのが、だんだん数字ごとに似たような場所に集まっているのがわかりますね。100epoch目の画像はこちらです。

t-SNEと比べて、明らかにクラス単位で同じ場所に寄っていますね。softmax関数によるクラス分類もこの特徴量を使っているので（CNNの構成により）、これはsoftmax関数の判断根拠を示しているにすぎません。AutoEncoderと異なり逆変換に相当するレイヤーを定義していないので、分散比の計算的なことはできませんが、分類の精度をこの代替指標とすることができます。長所短所を考えると次のようになります。

CNNによる可視化の長所・短所

長所短所を考えてみました。長所

ただの分類問題なので、学習が簡単で安定する。AutoEncoderのレイヤー数が半分でよい
次元の拡張が容易（tanhのユニット数を増やせば良いだけ）で計算速度をほとんど犠牲にしない。t-SNEのような3次元以下の制約がない
主成分分析の系列はデータによって固有ベクトルが変わってしまうが、X→特徴量のマッピングはCNNだと固定で明確に定義できる
転移学習が使える
Bias/Varianceの分析により、データに対する汎化的な次元削減を提供できる。訓練データに対する精度・開発データに対する精度を見れば容易に調整できる

続いて短所

ラベルがないとそもそも分類問題に落とし込めない。MNISTのようにこの数字は0、1…というラベルが必要。AutoEncoderやt-SNEの場合はいらない（はず）
固有ベクトルが何なのか表すのが難しくなる。X→特徴量のマッピングが巨大なCNNそのものになるから。ただし、t-SNEやAutoEncoderを使っても同様の問題はある。
AutoEncoderや、t-SNEをニューラルネットワークで表現したほうがおそらく厳密になる。AutoEncoderの場合は元画像との分散を計算できるし、t-SNEの場合はKLダイバージェンスの最小化という保証がつく

なので簡易版でしょうか。ただ、転移学習やBias/Varianceが使えたり、次元の拡張が容易だったりとかなりメリットは大きいと思います。AutoEncoderも転移学習できるらしいので「ならAutoEncoder使えよ」という感はありますが、EncoderはあってもDecoderの学習済みモデルってそこまでなさそうな。

まとめ

可視化のための次元削減手法として、PCA, Kernel-PCA, t-SNE, CNNを比較しました。各手法のプロットを再掲して終わりにします。

PCA

Kernel-PCA

t-SNE

CNN

PCA, Kernel-PCA, t-SNE, CNNによる可視化のための次元削減の比較

目次