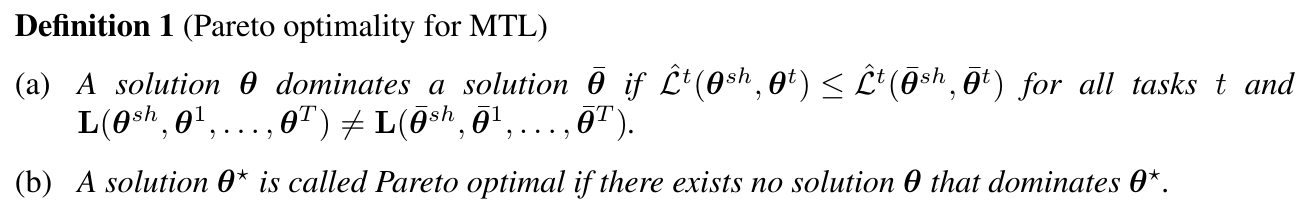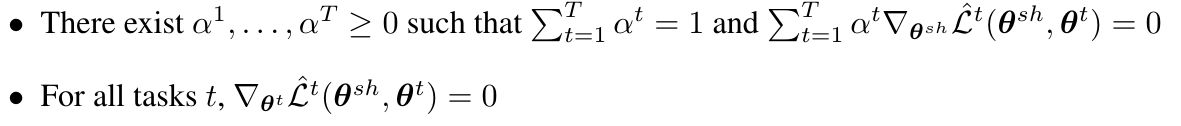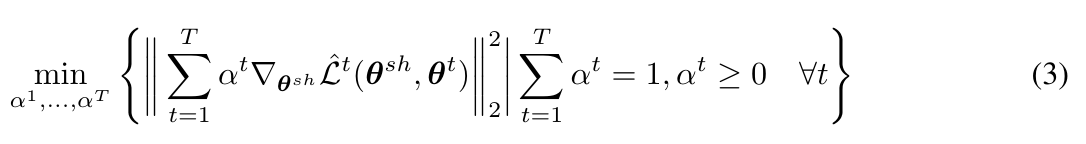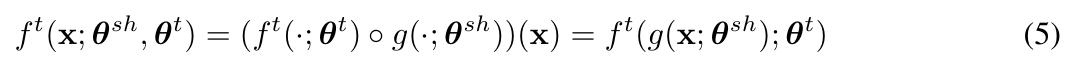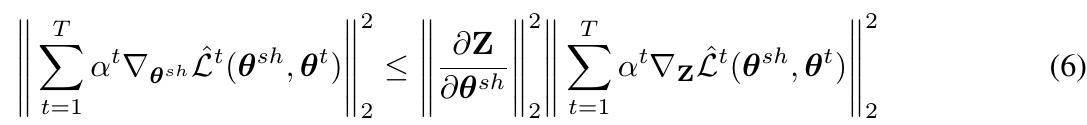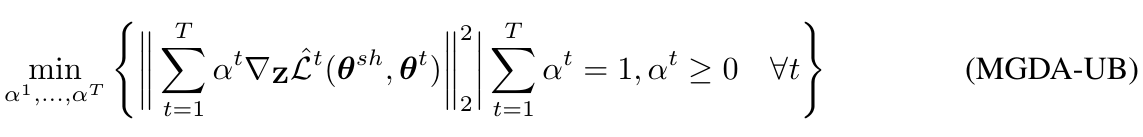論文紹介: Multi-Task Learning as Multi-Objective Optimization

tl;dr

• Sener and Koltun. 2018. Multi-Task Learning as Multi-Objective Optimization. NIPS.
• マルチタスク学習では、相乗効果に各タスクの性能が上がってゆきますが、ある程度学習器が各タスクに適合してくると、各タスクの目的が競合してくることがある。
• 他のタスクの性能を下げることなく、タスク性能を向上することができる学習方法、つまりマルチタスク学習においてパレート最適な解を見つける勾配法に基づく学習方法を提案。本手法は従来手法と異なり深層学習にスケールする。
• 提案手法が(ゆるい前提条件のもとで)常にパレート最適な解を見つけることを証明し、実験的にもベースラインと先行研究より優れていることを示した。

はじめに

マルチタスク学習

近年、マルチタスク学習（Multi-task learning; MTL）が注目されています¹。マルチタスク学習では、異なる性質²を持つタスクを1つの学習器でときます。

マルチタスク学習を使うことによって、補タスク（auxiliary tasks）の学習から得た教師信号をもとに興味がある主タスクの性能を向上することができます（e.g. 文から"誰が、誰に対して、何をしたか"と言った情報を抽出する問題を解くために、各単語の品詞を当てるタスクを同時に解く³）。あるいは、いくつかのタスク全てに興味がある場合に、それらのタスクの学習の相乗効果により、各タスクの性能向上を図ります。また、複数のタスクを1つの学習器で解くことによって、学習時間や総パラメータ数を減らせるというメリットもあります。

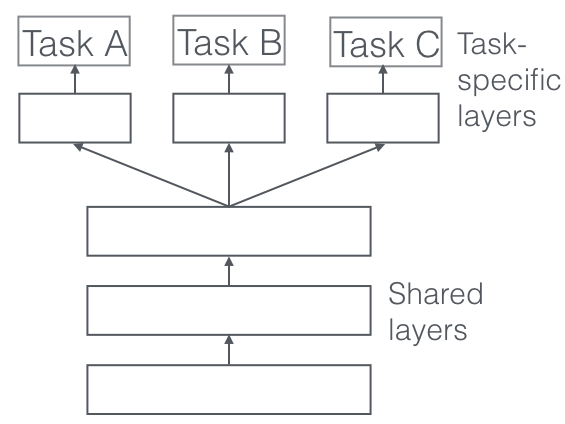
(Picture from http://ruder.io/multi-task/)

マルチタスク学習自体は古くからある概念なのですが、近年の深層学習の興隆により注目を集めています。深層学習では、確率的勾配方とチェインルールにより、様々な形状のニューラルネットワークを学習できるため、例えば上記の図のように1つのネットワークにタスクを複数つけることで、簡単にマルチタスク学習器を作ることができあｍす。本研究は、そのような深層学習のパラダイムにおけるマルチタスク学習の学習方法について研究したものになります。

本研究の目的

本研究では、前述した2つのマルチタスク学習の目的のうちの後者、つまりいくつかのタスク全てに興味がある場合に、それらのタスクの学習の相乗効果により、各タスクの性能向上を図る場合を対象にします。マルチタスク学習を行うと相乗効果に各タスクの性能が上がってゆきますが、ある程度学習器が各タスクに適合してくると、各タスクの目的が競合してくることがあります。本研究では、マルチタスク学習において各タスクが競合しだしたときに、他のタスクの性能を下げることなく、タスク性能を向上することができる学習方法、つまりマルチタスク学習においてパレート最適な解を見つける学習方法を提案します。特に、本研究では単に実験的にうまくいくだけではなく、提案する学習手法が常にパレート最適な解⁴を見つけることを証明します。

なお、パレート最適なマルチタスク学習手法自体は先行研究にもありますが、それらの手法は深層学習にスケールしないという問題がありました。そこで、本研究では深層学習にスケールするような手法を提案します。

手法

マルチタスク学習のパレート最適

上記に記載した図のように、1つのモデルから複数タスクの枝が伸びているような深層学習手法をイメージしてください。各タスクの損失が与えられたときに、一般的なマルチタスク深層学習では、次式のように各タスクの重み付き和を損失関数として、確率的勾配法でパラメータを学習します。

グローバルな最適解に必ずしもたどり着かない深層学習でこのような損失関数を最小化すると、各タスクの損失がうまくバランスされることは保証されません。最悪の場合、いくつかのタスクは発散し、残りのタスクの損失だけが最小化されることもありえます。

そのような問題に対して、本研究ではパレート最適なパラメータを見つけることを目指します。ここで、もう少し厳密にパレート最適を定義すると:

(a)は、ある解A(左辺)において、全てタスクの損失がある解B(右辺)の対応する損失よりも小さい状態を、解Aが解Bをdominateする状態だと定義しています。(b)によると、何にもdominateされない解があるとき、それをパレート最適な解と呼びます。つまり、パレート最適な解においては、いずれかのタスクの性能を犠牲にしない限り、タスク性能の向上は図れないことを意味します。逆に、パレート最適でない解においては、いずれのタスクの性能をも犠牲にしないでタスク性能の向上はかる余地があります。このことから、マルチタスク学習においてパレート最適な解を見つけることの嬉しさが伝わるのではないかと思います。パレート最適な解は複数（多くの場合無限に）存在します。

パレート最適な勾配法 (Multiple Gradient Descent Algorithm; MGDA)

マルチタスク学習において、KKT(Karush–Kuhn–Tucker)条件によると、次の2つの条件が満たされた解はパレート最適です⁵。

さらに、次式で与えられる勾配が0の場合はKKT条件が満たされパレート最適な解が得られることが保証されます。0ではない場合は、必ず全タスクの性能が向上する (少なくとも低下はしない) パラメータの更新を与えます。

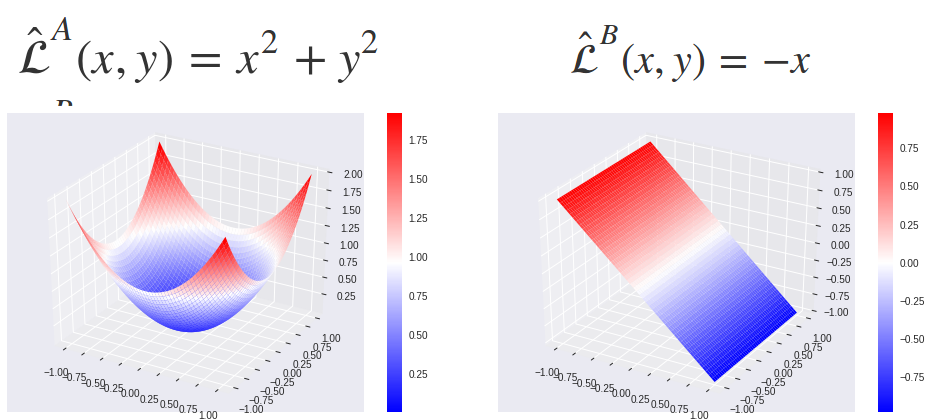
この式の証明は本研究で引いている論文にてなされているようなのですが、それを完全に理解するのは大変なので、簡単な例を使って理解します。この例では1つのデータと、2つのタスクだけがあり、2つのタスクの損失関数は、(タスク共通の)2つのパラメータ$x$と$y$によって与えられるものとします。

\begin{align}
  \hat{\mathcal{L}}^A(x, y) &= x^2 + y^2 \\
  \hat{\mathcal{L}}^B(x, y) &= -x
\end{align}

タスクAの損失関数はお玉状、タスクBの損失関数は傾いた平面です。

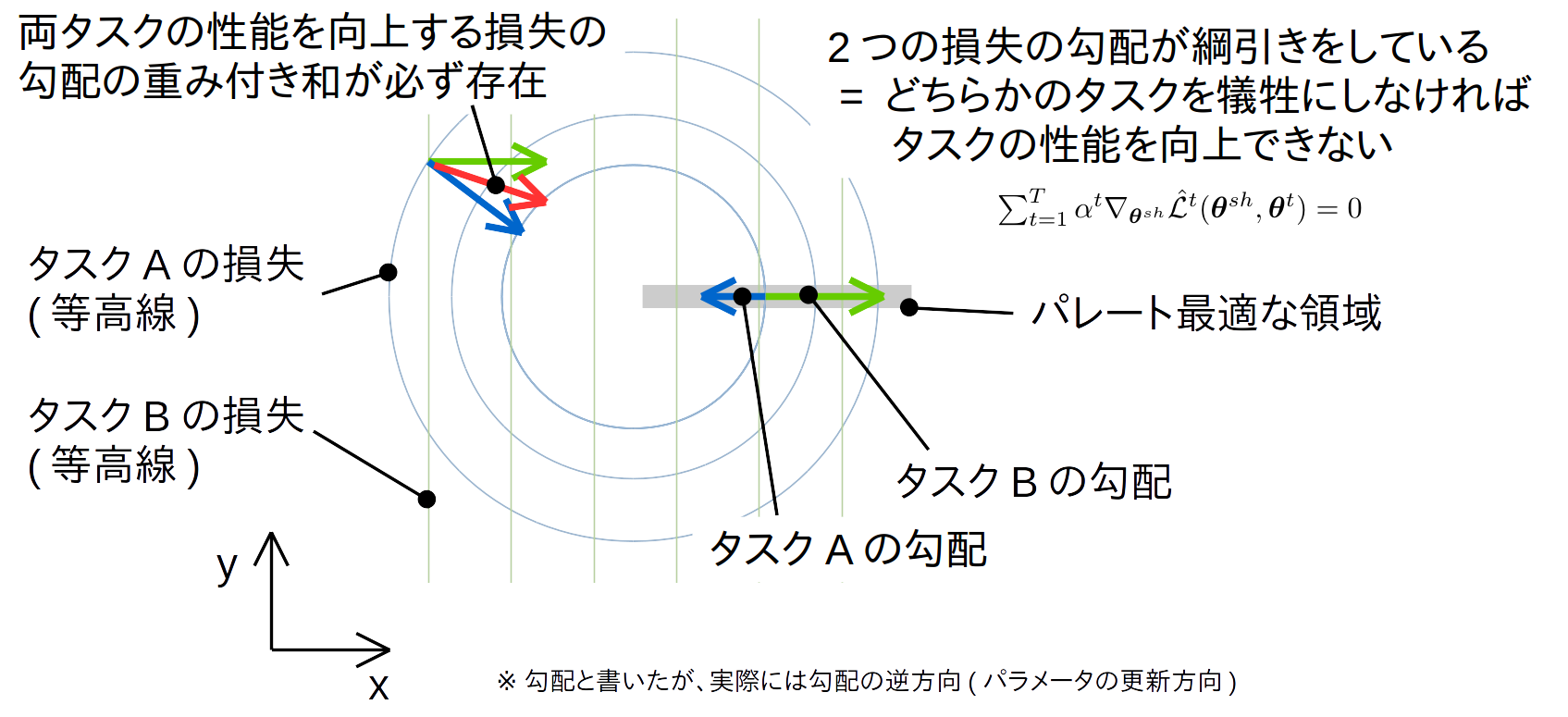
これらの損失関数を等高線として平面上に図示します。青、緑の矢印はそれぞれの損失関数の勾配に-1をかけたもの (=パラメータ更新の方向)を示しています。

2つのタスクの勾配が逆方向を向いて綱引きをしている状態がパレート最適な状態です。このとき、勾配の大きさには意味がありません。方向が真逆なので、程度の差はあれど、片方のタスクの損失を減らすことが、他方の損失を増やすことにつながります。勾配の和を適当にスケーリングしたものが釣り合う = 和が0になるということで、この状態が前述したKTT条件の1つ目の項目に相当します。

勾配の和がつりあっていない場合では、2つの勾配の間のベクトル (= 2つの勾配の重み付き和) を適当にとってやることで、2つのタスクの損失を減らせる勾配がありそうなことがなんとなくわかると思います。

KTT条件の2点目は各タスクに独立なパラメータが極小値となる点なので、一般的な勾配法の話をしているだけになります。

以上より、パレート最適な勾配法は、各更新ステップごとに損失関数の勾配をどのような比で混ぜあわせるかを決定する問題になることがわかりました。さらに、勾配の比は前述した式(3)によって与えられることがわかりました。次節以降で、この式(3)をどのように求めるかを考えてゆきます。

MGDAの最適化

前述した損失関数の勾配を混ぜあわせる比率$\alpha^t$(式(3))をどのように計算するかを説明します。また、上記で出した簡単な例を使って説明します。ここでは、上記の2Dの図に図示したように$(-1, 1)$の点の$\alpha^t$を求めたいと考えます。

\begin{align}
  \frac{\partial\hat{\mathcal{L}}^A(x, y)}{\partial x} &= 2x \\
  \frac{\partial\hat{\mathcal{L}}^A(x, y)}{\partial y} &= 2y 
\end{align}

したがって、

\nabla\hat{\mathcal{L}}^A(-1, 1) =   \left( {\begin{array}{cc}
   2x \\
   2y \\
  \end{array} } \right) = \left( {\begin{array}{cc}
   -2 \\
   2 \\
  \end{array} } \right)

同様に、

\nabla\hat{\mathcal{L}}^B(-1, 1) =   \left( {\begin{array}{cc}
   -1 \\
   0 \\
  \end{array} } \right)

式(3)に上記の式を導入し、

\begin{align}
\left\|\alpha^A \nabla\hat{\mathcal{L}}^A(-1, 1) + \alpha^B \nabla\hat{\mathcal{L}}^B(-1, 1) \right\|^2_2 &= \left\|\alpha^A\left( {\begin{array}{cc}
   -2 \\
   2 \\
  \end{array} } \right) + \alpha^B\left( {\begin{array}{cc}
   -1 \\
   0 \\
  \end{array} } \right)\right\|^2_2 \\
&= \left\|\left( {\begin{array}{cc}
   -2\alpha^A - \alpha^B\\
   2\alpha^A \\
  \end{array} } \right)\right\|^2_2 \\
&= (-2\alpha^A - \alpha^B)^2 + (2\alpha^A)^2 \\
&= 8(\alpha^A)^2+2\alpha^A\alpha^B + (\alpha^B)^2
\end{align}

minimize_{\alpha^A, \alpha^B}\qquad 8(\alpha^A)^2+2\alpha^A\alpha^B + (\alpha^B)^2 

subject to

\alpha^A + \alpha^B = 1 \\
0 \leq \alpha^A \leq 1 \\
0 \leq \alpha^B \leq 1

という形で、非線形計画法に落とせることがわかります。

この非線形計画法を深層学習の規模で解くことは現実的ではないので、著者らはこの問題をFrank-Wolfe algorithmで解くことを提案しました。Frank-Wolfe algorithmは制約付きの勾配法で、毎反復ごとに現在の周辺で一次テイラー展開を行い、それを線形計画法で最適化する方法(らしい)です。

著者らによると、深層学習に占める$\alpha^t$の計算時間は無視できるレベルで、結果もうまく収束しているとのことです。

MGDAの高速化

前述したMGDAでは、タスクごとに全パラメータについて$\nabla\hat{\mathcal{L}}^t(\mathbf{\theta}^{sh};\mathbf{\theta}^{t})$を計算していたので、非常に非効率でした。そこで本研究では深層学習で用いられるチェインルールによってこの計算を簡略化します。

まず、この簡略化を行うために次のような前提をおいています。

つまり、入力データに対して、共通のパラメータ部分で変換を行ったあとに、タスクごとのパラメータによる変換を適用するということです。深層学習におけるマルチタスク学習ではこのような形式が一般的なので、本前提は多くの場合成り立つものと考えられます。

このとき、前述した式(3)から、チェインルールを使って次のような上界を導き出すことができます。

ただし、$\mathbf{Z} = (\mathbf{z}_1, ..., \mathbf{z}_N)$、$\mathbf{z}_i=g(\mathbf{x}_i; \mathbf{\theta}^{sh})$です。チェインルールを使っているのにもかかわらず不等式なのは、フロベニウスノルムの外に式をはき出す際に三角不等式が成立するからです。

$\partial\mathbf{Z}/\partial\mathbf{\theta}^{sh}$の部分はタスクによらず固定の値なので、前述した$\alpha$の計算をするときは省くことができます。したがって最終的には次のような目的関数を得ます、

実装的には、次のようになると考えらます。

• 一般的な深層学習と同様に順方向計算をする。
• 各タスクの損失から$\mathbf{Z}$における勾配をそれぞれバックプロパゲーションで計算する。
• $\mathbf{Z}$における勾配を使い上記のMGDA-UBの式から$\alpha^t$を決定する。
• $\mathbf{Z}$における勾配を$\alpha$でスケールしたあと、あとは通常通りにバックプロパゲーションする。

なお、MGDAは常にパレート最適な解を見つけることが証明されていましたが、その上界であるMGDA-UBが同様の性質を持つことは自明ではありません。そのため、著者らはMGDA-UBも同様の性質を持つことを証明しています。

実験

マルチラベル分類問題における精度比較

マルチラベル分類がマルチタスク学習であるかは意見がわかれるところですが、著者らはまずマルチラベル問題に提案手法を適用しています。

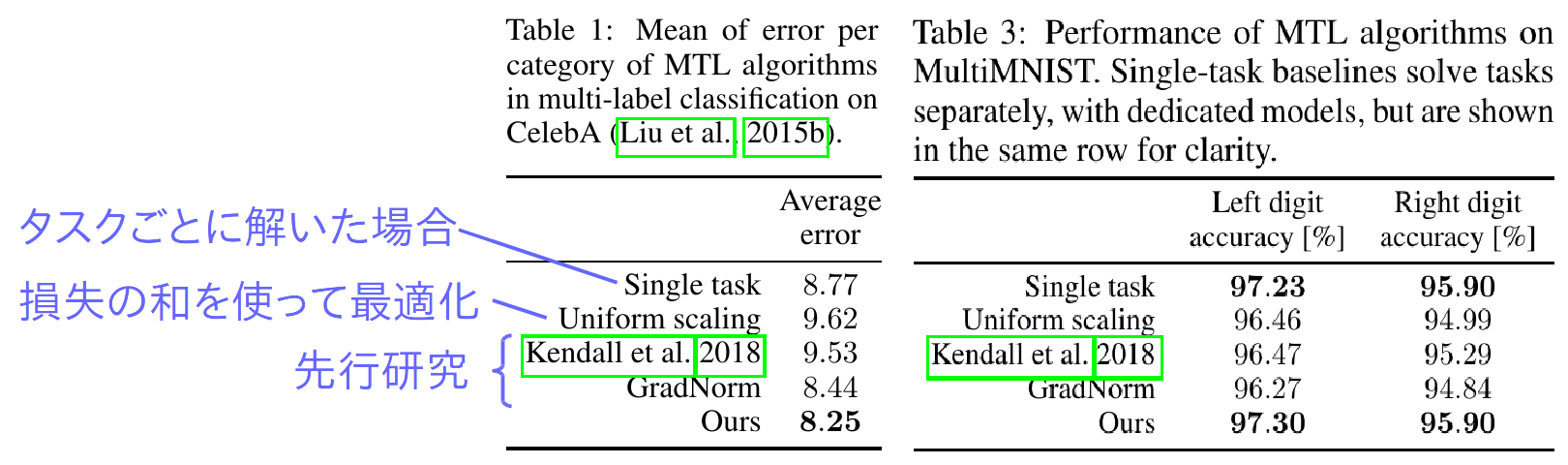
(Table from the paper, blue annotation by koreyou)

Table 1はCelebA (顔写真に対して"ひげ"、"笑顔"といった顔の特徴を表す2値ラベルを付与)、Table 2はMultiMNST (2つの数字を重ねあわせてマルチタスク化したデータセット)における性能をしめしています。タスクをバラバラに二値分類器でといたり、一般的なマルチタスク学習でやるように損失の和を最適化したりするベースラインに比べても、またマルチタスク学習に関する先行研究に比べても提案手法が優れていることがわかります。

マルチタスク問題 (Scene understanding) における精度比較

今度は、画像を入力にsemantic segmentation ("車"、"道路"などピクセルごとに物体ラベルを決定する)とinstance segmentation ("車A"、"車B"のようにピクセルごとに個別の物体を見分ける)、depth estimation (ピクセルごとに奥行き距離を推定する)を解いた時の性能を比較しています。

(Table from the paper, blue annotation by koreyou)

提案手法が、どのタスクでも一貫してベースラインを上回っていることがわかります。

学習にかかる時間

本研究の貢献の一部は上記の"MGDAの高速化"で説明したMGDAの上界を最適化する手法です。この工夫を導入することで計算時間がどのくらい減るのかを検証しています。

(Table from the paper)

従来タスクの数に対して線形にバックプロパゲーションの回数が増えていたところ、この工夫を使うと1回で済むということでした。実際に表右側のMulti-labelとなっているところでは、学習時間が概ね1/40になっています。オーバーヘッドの影響なのか、Scene understandingでは1/3とまではいきませんが、こちらでも大幅な学習時間の削減が実現できています。

この工夫ではMGDAの近似を行っているのですが、どのタスクでも性能は落ちていません。これは著者らが証明したとおり、この工夫を行ったMGDA-UBもやはりパレート最適な勾配を与えるからです。

コメント

• 深層学習で汎用的に使え、理論保証があるマルチタスク学習ということで非常に実用的＋興味深い。
• 本研究ではパレート最適であることが保証されるが、逆にいえば望ましくないパレート最適な解に収束してしまうこともあるのではないだろうか。例えば、あるタスクの性能を1%落とせば、他のタスクの性能が10%上がる場合、など。どのような問題でうまく行かないかについてもわかるとよかった。

編集可能な図はこちら。

1. 近年のマルチタスク学習の動向については、Ruderさんによる素晴らしいまとめ記事(英語)をご覧ください。 ↩

2. 業界レベルでコンセンサスが取れているかは不明ですが、通常、出力の形式が異なる問題をマルチタスク学習と呼び、分類タスクを複数同時に行うマルチラベル学習とは区別します。本論文ではマルチラベル学習もマルチタスク学習の一部として実験をしています。 ↩

3. 先週紹介した、Strubell et al. 2018. Linguistically-Informed Self-Attention for Semantic Role Labeling. EMNLP. ↩

4. パレート最適が保証されるのはバッチ学習、あるいはミニバッチ学習における1回の更新の部分だけです。ミニバッチ学習における大域最適解、テストデータにおけるパレート最適については(私が理解限りした限りでは)本論文では述べていません。 ↩

5. 厳密にいうと、この条件が満たされた解はPareto stationaryだそうです。パレート最適な解は必ずPareto stationaryですが、pareto stationaryであったとしてもパレート最適とは限りません。pareto stationaryがパレート最適ではない例は簡単に思いつきます。例えば上記で述べた2次元の場合でも、Aの損失を非凸の関数に変えるだけで、大域最適解でないほうの局所最適解そばに、パレート最適でないpareto stationaryな領域ができることがわかります。本論文では、なぜpareto stationaryで良いかについては特に述べられていません。深層学習においてはほとんどの局所最適解が大域最適解に近いということがわかってきており、同様のことが提案手法の勾配法においても言えるのではないかと私は想像しています。 ↩