はじめに
流行りの機械学習、実際どんな計算しているの?
ということで、流行りのSwiftで実装してみました。
最初は教師あり学習であるロジスティック回帰。
ロジスティック回帰とは、パーセプトロンと同じ分類アルゴリズムであり、最尤推定法で分割線のパラメーターを決定するアルゴリズムです。
つまり、「新しく与えられたデータは$t=1$に属する」 という推定だけではなく、 「新しく与えられたデータが$t=1$に属する確率は70%」 という、確率的な推定ができるようになります。
ITエンジニアのための機械学習理論入門を参考に、ロジスティック回帰についてまとめさせていただいた資料をこちらに用意しました。今回は資料に沿って説明していきたいと思います。
手順
ロジスティック回帰では、以下の3STEPで分類問題を解きます。
- 得られたデータが、ある属性値を持つ確率(事後確率)を設定しておき
- そこから逆に、トレーニングセットのデータが得られる確率(尤度関数)を計算する
- そして、尤度関数が最大になるように、1.に設定した確率の式に含まれるパラメーターを決定する
補足として、トレーニングセットは最も発生確率が高いに違いない!という仮説が正しいものとして、トレーニングセットのデータが得られる確率「尤度関数」が最大になるようにパラメーターを決定する手法を「最尤推定法」と呼びます。
例題
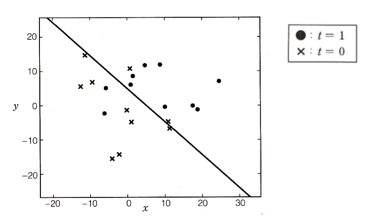
今回は、$(x,y)$平面上にある、$t=0$,$1$の属性値を持つトレーニングセットを元に、新たなデータ$(x,y)$が与えられたときの$t$を確率的に推定しなさい。という問題を解くことにします。
つまり、$(x,y)$平面上の直線を最尤推定法を用いて決定することが目標です。
実装
トレーニングセットの用意
まずは、トレーニングセットを用意し描画していきます。コードはViewControllerにベタベタ書いています。
//トレーニングデータを生成
func setData(){
//データを初期化
TrainDataArray = []
//正解直線をランダムに決定する
answerLine = WeightVector3(a: getRandomNumber(Min: -1.0, Max: 1.0), b: getRandomNumber(Min: -1.0, Max: 1.0), c: getRandomNumber(Min: -1.0, Max: 1.0))
print("AnswerLine :",answerLine.a,"*x + ",answerLine.b,"*y + ",answerLine.c)
drawAnswerLine(answerLine)
while TrainDataArray.count < N{
let x:Float = randn()
let y:Float = randn()
var c:Int = Int()
if answerLine.a*x + answerLine.b*y + answerLine.c >= 0{
c = 0
}else{
c = 1
}
let test = TrainData(x: x, y: y, c: c)
//描画
let point = UIView(frame:CGRectMake(
CGFloat(x*(Float(self.view.frame.width)/6) + Float(self.view.frame.width)/2)-12,
CGFloat(y*(Float(self.view.frame.width)/6) + Float(self.view.frame.height)/2)-12,
12,12))
point.layer.masksToBounds = true
point.layer.cornerRadius = point.frame.size.width/2.0
point.tag = TrainDataArray.count + 1
if c == 0{
point.backgroundColor = UIColor(red: 239/255.0, green: 83/255.0, blue: 80/255.0, alpha: 1.0)//赤
}else{
point.backgroundColor = UIColor(red: 66/255.0, green: 165/255.0, blue: 245/255.0, alpha: 1.0)//青
}
TrainDataArray.append(test)
self.view.addSubview(point)
}
}
わかりやすいように構造体を作ってます。
protocol Data{
var x:Float { get set }
var y:Float { get set }
var c:Int { get set }
}
struct TrainData: Data {
var x:Float
var y:Float
var c:Int
}
protocol Vector3{
var a:Float { get set }
var b:Float { get set }
var c:Float { get set }
}
struct WeightVector3: Vector3 {
var a:Float
var b:Float
var c:Float
}
乱数を生成する関数はこんな感じ。
func getRandomNumber(Min _Min : Float, Max _Max : Float)->Float {
return ( Float(arc4random_uniform(UINT32_MAX)) / Float(UINT32_MAX) ) * (_Max - _Min) + _Min
}
//正規乱数
func randn() -> Float{
let randn = getRandomNumber(Min: 0.0, Max:1.0) + getRandomNumber(Min: 0.0, Max:1.0)
+ getRandomNumber(Min: 0.0, Max:1.0) + getRandomNumber(Min: 0.0, Max:1.0)
+ getRandomNumber(Min: 0.0, Max:1.0) + getRandomNumber(Min: 0.0, Max:1.0)
+ getRandomNumber(Min: 0.0, Max:1.0) + getRandomNumber(Min: 0.0, Max:1.0)
+ getRandomNumber(Min: 0.0, Max:1.0) + getRandomNumber(Min: 0.0, Max:1.0)
+ getRandomNumber(Min: 0.0, Max:1.0) + getRandomNumber(Min: 0.0, Max:1.0)
return randn - 6.0
}
1.得られたデータがある属性値を持つ確率
はじめに、$(x,y)$平面上の直線を表す線形関数を次式で定義します。
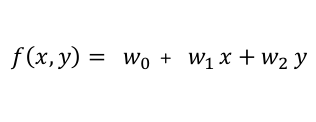
var weightVector:WeightVector3 = WeightVector3(a: getRandomNumber(Min: -1.0, Max: 1.0), b: getRandomNumber(Min: -1.0, Max: 1.0), c: getRandomNumber(Min: -1.0, Max: 1.0))
次に、$(x,y)$平面上のデータの属性が$t=1$である確率を計算します。
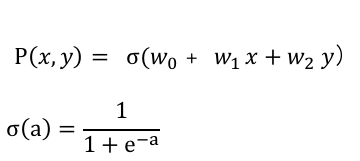
func getProb(x:Float, y:Float, weightVector:WeightVector3) -> Float{
let feature_vector = TrainData(x: x, y: y, c: 1)
let a = inner(feature_vector, right: weightVector)
return sigmoid(a)
}
ここで登場するのがロジスティック関数です。
func sigmoid(a:Float) -> Float{
let sig = 1.0/(1.0 + exp(-a))
return sig
}
2.トレーニングセットのデータが得られる確率
先ほど求めた確率をもとに、トレーニングセットとして与えられたデータが得られる確率$P$を考えます。
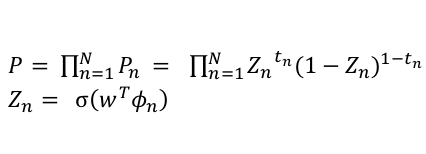
ここで$Z_n$は$n$番目のデータの属性が$t=1$である確率を表します。

トレーニングセットが得られる確率$P$を、$Z_n$を通してパラメーター$w$の関数として見た上式が尤度関数です。詳しい式の導出は資料を参考にしてください。
func likelihood(weightVector:WeightVector3) -> Float{
var likelihood:Float = 0.0
for (index,trainData) in TrainDataArray.enumerate(){
let prob = getProb(trainData.x,y: trainData.y,weightVector: weightVector)
//行列生成
var j = 0
var r:[Float] = []
while j < N{
if j == index{
r.append(prob*(1.0-prob))
}else{
r.append(0)
}
j += 1
}
R.append(r)
var z:[Float] = []
z.append(prob-Float(trainData.c))
Z.append(z)
var iLikelihood:Float = 0.0
if trainData.c == 1{
if prob == 0.0{
iLikelihood = 0
}else{
iLikelihood = log(prob)
}
}else if trainData.c == 0{
if prob == 1.0{
iLikelihood = 0
}else{
iLikelihood = log(1.0-prob)
}
}
likelihood = likelihood - iLikelihood
}
return likelihood
}
3.尤度関数が最大になるようにパラメーターを決定
次に、尤度関数が最大になるようにパラメータ$w$を決定していきます。
ここでは、確率$P$の値が大きくなる方向に$w$を修正する手順を繰り返す、ニュートン・ラフソン法を用いります。
ニュートン・ラフソン法とは、$f(x)=0$となる$x$を次式を用いて求める「ニュートン法」 を多次元・非線形に拡張した手法です。
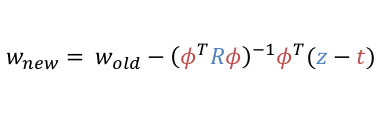

パラメーター$W_{old}$が与えられた際に、 $z$と$R$を計算しておき、修正された新しいパラメーター$W_{new}$を決定する。$W_{new}$を$W_{old}$としてさらに新しい$W_{new}$を計算することを繰り返すと確率$P$の値が大きくなり、最終的に最大値に達します。
また、上式の計算を繰り返すと、$P$の値が最大値に近づくにつれて、パラメーター$w$の変化の割合は小さくなっていきます。そこで、変化の割合が閾値を切った時点で計算を打ち切ることにします。
以上を踏まえたコードがこちらです。
var oldWeightVector:[WeightVector3] = []//検討したパラメータ
var beforeWeightVector = weightVector//一つ前のパラメータ
//z=1を持つデータ行列
var trainMat: [[Float]] = []
for trainData in TrainDataArray{
trainMat.append([1.0,trainData.x,trainData.y])
}
let trainTransposedMat = transposed(trainMat)
//尤度関数が最大になるようにパラメータを決定する
while count < 100{
R = []
Z = []
likelihood(weightVector)//最尤推定
oldWeightVector.append(weightVector)
//パラメータを計算
let r1 = product(trainTransposedMat,matB:R)
let r2 = product(r1, matB: trainMat)
let r3 = invers(r2)
let r4 = product(r3, matB: trainTransposedMat)
let result = product(r4, matB: Z)
//パラメータを更新
beforeWeightVector = weightVector
weightVector = WeightVector3(a: beforeWeightVector.a - result[1][0], b: beforeWeightVector.b - result[2][0], c: beforeWeightVector.c - result[0][0])
print(weightVector)
//変化率が閾値を切った時点で終了
if ((weightVector.a - beforeWeightVector.a)*(weightVector.a - beforeWeightVector.a) + (weightVector.b - beforeWeightVector.b)*(weightVector.b - beforeWeightVector.b) + (weightVector.c - beforeWeightVector.c)*(weightVector.c - beforeWeightVector.c))/(beforeWeightVector.a * beforeWeightVector.a + beforeWeightVector.b * beforeWeightVector.b + beforeWeightVector.c * beforeWeightVector.c) < 0.00001{
weightVector = beforeWeightVector
print("END")
break
}
count += 1
}
ここでは、3x3行列の計算を関数化しました。(便利なライブラリあったのかな?)
行列の積
func product(matA:[[Float]],matB:[[Float]]) -> [[Float]]{
var resultMat:[[Float]] = []
var re = 0
while re < matA.count{
resultMat.append(Array(count: matB[0].count, repeatedValue: 0))
re += 1
}
var i = 0
while i < matA.count{//左の行分回す
var j = 0
while j < matB[0].count{//右の列分回す
var k = 0
while k < matB.count{//右の行分回す と 左の列
resultMat[i][j] += matA[i][k] * matB[k][j]
k += 1
}
j += 1
}
i += 1
}
return resultMat
}
逆行列
func invers(mat:[[Float]]) -> [[Float]]{
var resultMat:[[Float]] = []
var det:Float = 0.0
var re = 0
while re < 3{
resultMat.append(Array(count: 3, repeatedValue: 0))
re += 1
}
for i in 0 ... 2{
var right:Float = 1.0
var left:Float = 1.0
for j in 0 ... 2{
right *= mat[(i+j)%3][j%3]
left *= mat[(i+3-j)%3][j%3]
}
det = det + right - left
}
if det == 0{
return resultMat
}else{
for i in 0 ... 2{
for j in 0 ... 2{
let aaa = mat[(i+1)%3][(j+1)%3] * mat[(i+2)%3][(j+2)%3]
let bbb = mat[(i+1)%3][(j+2)%3] * mat[(i+2)%3][(j+1)%3]
resultMat[j][i] = ( aaa - bbb ) / det
}
}
}
return resultMat
}
転置行列
func transposed(mat:[[Float]]) -> [[Float]]{
var resultMat:[[Float]] = []
var re = 0
while re < mat[0].count{
resultMat.append(Array(count: mat.count, repeatedValue: 0))
re += 1
}
var i = 0
while i < mat[0].count{//列
var j = 0
while j < mat.count{//行
resultMat[i][j] = mat[j][i]
j += 1
}
i += 1
}
return resultMat
}
仕上げと結果
あとは描画関係をいろいろ書き足して、完成。
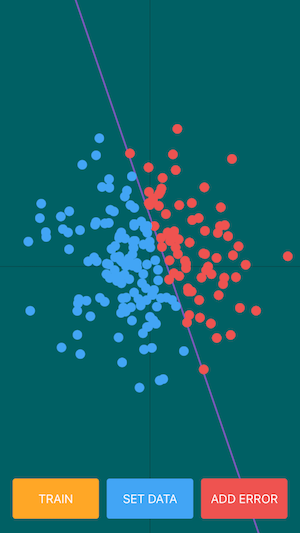
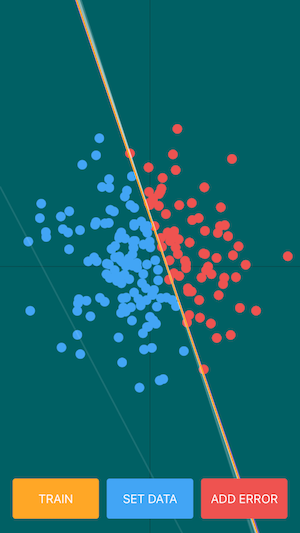
左図の紫色の線が正解直線、右図の黄色い線が推定線です。
それらしい分類線を引けること、最初に設定した正解線に近い線を推定できていること、を確認できると思います。
 →
→ 
これだけでは正確な推定すぎてつまらないので、データセットにエラーデータを追加するコードを追加。
@IBAction func Error(sender: AnyObject) {
print("Error")
let subviews = self.view.subviews
for (index,trainData) in TrainDataArray.enumerate(){
if arc4random_uniform(100)%20 == 0{
if trainData.c == 0{
TrainDataArray[index] = TrainData(x: trainData.x, y: trainData.y, c: 1)
for subview in subviews {
if subview.tag == index + 1{
subview.backgroundColor = UIColor(red: 66/255.0, green: 165/255.0, blue: 245/255.0, alpha: 1.0)
}
}
}else if trainData.c == 1{
TrainDataArray[index] = TrainData(x: trainData.x, y: trainData.y, c: 0)
for subview in subviews {
if subview.tag == index + 1{
subview.backgroundColor = UIColor(red: 239/255.0, green: 83/255.0, blue: 80/255.0, alpha: 1.0)
}
}
}
}
}
}
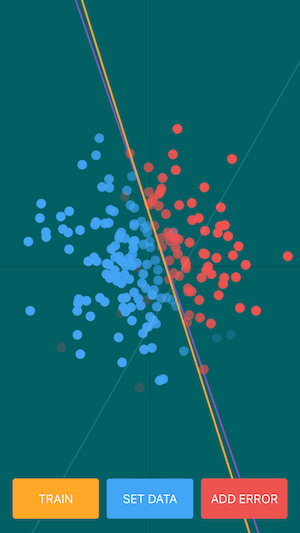
左図がエラーデータ追加状況、右図が推定結果です。
透過度が低い(濃い)ほど正解である確率が高く、透過度が高い(薄い)ほど正解である確率が低い結果としています。
ある程度エラーデータがあると、データが各属性値を持つ確率が揺らいでいる様子が伺えて面白いです。
 →
→ 
おわりに
コード全体をGitで公開しています。
https://github.com/koooootake/LogisticRegression
以上です、閲覧ありがとうございました🙏