wgld.orgの管理人であるdoxasさん主催のWebGLスクールの第四回目です。
今回は3Dプログラミングには欠かせない行列とクォータニオンについての講座でした。
前回の講座でも行列は使っていますが、今回からより深く行列について学びました。
前回までのまとめ
第一回 WebGLスクール 「WebGLの概念」
第二回 WebGLスクール 「WebGLの手続きと手順」
第三回 WebGLスクール 「シェーダの基礎」
行列とは??
行列とは、同じ箱に数値が詰め込まれているような構造をしていて、たくさんの情報を保持することができる数学の概念です。
3Dプログラミングではとても重宝されていて、欠かせないもの。難しいというか面倒。
行列との向き合い方
3Dプログラミングにおいて行列は 座標の変換 が主な利用目的となる。
行列の計算方法を理解するのはとても大変なので、まずは、 行列を用いて座標を変換する使い方 を覚えてしまう方がいいそうです。
最低限覚えておきたい行列の種類
最低限以下の4種類の行列の意味を理解しておく。
- 正方行列
- 単位行列
- 転置行列
- 逆行列
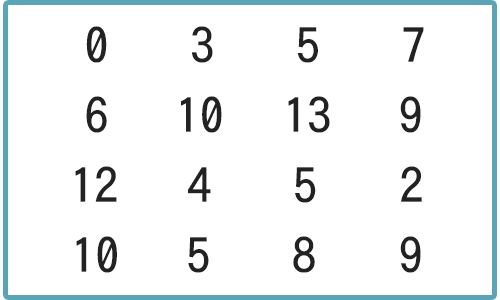
正方行列
正方行列は、 列と行が同じになる行列 のこと。4×4、3×3、2×2など。
3Dプログラミングでは、4×4を利用することが多いが、3×3、2×2の行列も理解しておくと役に立つ。
WebGLで行列と言った場合は、普通は正方行列を表しています。
単位行列
単位行列は、 計算結果に変化を及ぼさない最小の単位に整えられた行列 のこと。
十進数の数値のように、行列にも0や1の状態という概念が存在する。
0の状態の行列を掛けると、どんな行列も0になる。
1の状態の行列を掛けると、どんな行列も中身は一切変化しない。
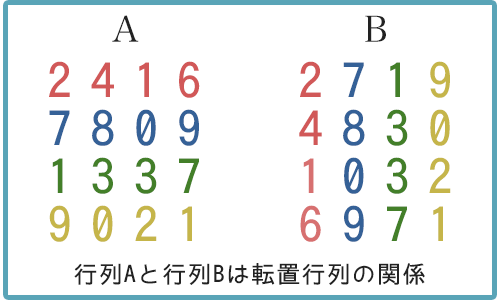
転置行列
転置行列は、何かと何かが置き換わっている行列のこと。
ある状態の 行と列を入れ替えた行列 ことを転置行列を呼びます。
逆行列
逆行列は、転置行列のように数値が反転しているイメージを持ちやすいが、全くべつもの。
ちょっと言葉での説明が難しいので、スクール資料の一部を引用します。
たとえば行列 A と行列 B を掛け合わせ、行列 C ができるとする。このとき行列 C に、行列 B' を掛け合わせると、計算結果が行列 A に戻るとする。
この行列 B' こそが逆行列で、言葉で表すなら「行列 B' は、行列 B の逆行列である」と言える。
つまり逆行列とは、ある行列の影響を そっくりそのまま打ち消してしまう行列 ということ。
この逆行列は非常に大事な概念なので、しっかりと覚えておく必要がある。
行列の乗算
3Dプログラミングでは、減算よりも乗算を使うことが多い。
通常の数値の掛け算では、5×10は50、10×5も50です。
しかし、行列においての掛け算では、 掛ける順序によって全く異なる結果になる。
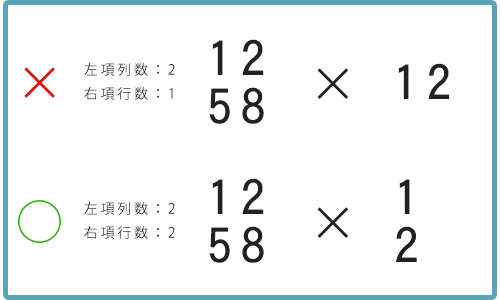
行列を掛け合わせるには、 左項の列数 と 右項の行数 が一致しなくてはならない。
つまりこういうこと↓↓↓
頂点シェーダのコードを見てみるとこのルールを守るために行列の変換が行われています。
attribute vec3 position;
uniform mat4 mvpMatrix;
void main(){
gl_Position = mvpMatrix * vec4(position, 1.0);
}
変数mvpMatrixは4×4の正方行列なのに対し、変数posiitonは3×3の正方行列です。
このままでは列数と行数が一致していしないため掛け合わせることができません。
そのため、positionをvec4に変換してから掛けています。
座標変換
三次元空間に置かれている頂点を、二次元空間上に変換する時に行列が使われる。
アプリケーション側(javascript)で変換するための行列を用意し、シェーダに渡してジオメトリパイプライン内で変換が行われる。
行列の生成、計算を自力で行うのはとても大変なので、minMatrix.jsライブラリを使う。
行列の生成と初期化
minMatrix.jsのmatIVオブジェクトが生成や加工などを行ってくれる。
// matIVオブジェクトを生成
var m = new matIV();
// 行列の生成
var matrix = m.create();
matrixは16個の要素が入った配列になっている。
単位行列の生成
単位行列を生成するには、identityメソッドを使用する。
行列が初期化された状態になります。
var nMatrix = m.identity(matrix);
座標変換の流れ
- ローカル座標系
- モデル座標系
- ビュー座標系
- プロジェクション座標系
ローカル座標系
ローカル座標系は一番初めに頂点が置かれている座標のこと。
つまり 素のモデルデータ。
一番始めの頂点データが(3,4,0)だった場合、この頂点座標がローカル座標系となる。
モデル座標系
モデル座標系は別名ワールド座標系とも呼ばれる。
レンダリングされるモデルをどんな位置、どんな姿勢、どんな拡大縮小を適応するのかを示した状態。
モデル座標系で、 空間上のどこにどのように配置されるかが決まる。
ビュー座標系
ビュー座標系ではカメラの位置を決定する。
カメラの位置、カメラの向き、カメラの上方向を適応する。
プロジェクション座標系
プロジェクション座標系では、三次元空間上にあったデータをスクリーンに投影する。
奥にあるデータは奥に配置し、手前のデータは手前に配置するという遠近法のような処理が行われる。
プロジェクション座標系まで行くと、スクリーンに映し出されるものが決まる。
座標系から座標系へ遷移するのに座標変換処理(行列)が必要になる
それぞれの座標系の処理例
それぞれの座標系を処理するにはminMatrix.jsを使います。
minMatrix.js公式リファレンス
モデル座標変換行列:平行移動
モデル座標系を大きく別けると 平行移動・回転・拡大縮小の3種類。
平行移動を行うには、translateメソッドを使う。
// 平行移動を行う場合の例
m.translate(mMatrix, [1.0, 1.0, 1.0], mMatrix);
translate(元となる配列, 適応データ, 反映させる行列)を使うことで、平行移動ができる。
モデル座標変換行列:回転
回転を行う場合は、rotateメソッドを使う。
// xを軸に90度回転
m.rotate(mMatrix, Math.PI / 2, [1.0, 0.0, 0.0], mMatrix);
モデル座標変換行列:拡大・縮小
拡大・縮小を行う場合は、scaleメソッドを使う。
// 全ての軸に対し、0.5倍のスケールを適用
m.scale(mMatrix, [0.5, 0.5, 0.5], mMatrix);
ビュー座標変換行列
ビュー座標変換にはlookAtメソッドを使用する。
// 原点よりやや手前の位置にカメラを置く
var eye = [0.0, 0.0, 5.0];
// 注視点は原点を指定
var center = [0.0, 0.0, 0.0];
// カメラの上方向はYの正方向
var up = [0.0, 1.0, 0.0];
m.lookAt(eye, center, up, vMatrix);
lookAt(位置, 注視点, 上向き, 反映させる行列)を使うことで、空間をどのように投影するかを決まることができる。
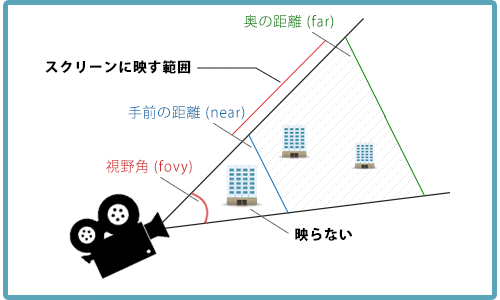
プロジェクション座標系
一般的な変換はperspectiveメソッドを使う。
// 視野角は45度に設定
var fovy = 45;
// コンテキストのアスペクト比
var aspect = canvas.width / canvas.height;
// クリッピング領域は0より大きい正の値を必ず指定する
var near = 0.1; var far = 100;
m.perspective(fovy, aspect, near, far, pMatrix);
perspective(視野角, アスペクト比, 手前, 奥, 反映させる行列)で投影反映を決定できる。
行列の掛け合わせ
三次元データをパイプライン内で二次元データに変換するためには、 モデル座標系、ビュー座標系、プロジェクション座標系 の3つが必要。
シェーダには一つずつ送るのではなく、3種類の座標系を全て掛け合わせてから送ればいい。
掛け合わせるにはmultiplyメソッドを使う。
// pMatrix = プロジェクション座標系
// vMatrix = ビュー座標系
// mMatrix = モデル座標系
// vMatrixにpMatrixを掛け、vpMatrixを生成
m.multiply(pMatrix, vMatrix, vpMatrix);
// mMatrixにvpMatrixを掛け、mvpMatrixを生成
m.multiply(vpMatrix, mMatrix, mvpMatrix);
掛ける順番に注意!! この順番はコピペでもいいのでしっかりと守る。
モデル座標変換の組み合わせ
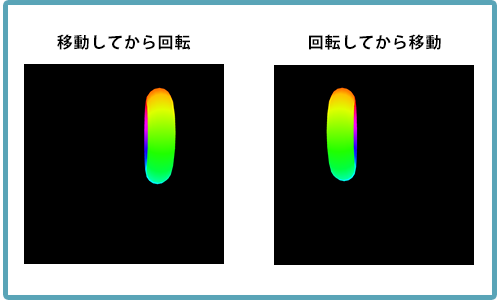
複数のモデル座標変換行列を掛け合わせる場合は、 掛ける順番 に注意しないと、思わぬ結果になってしまう。特に 回転 を使った場合は、掛ける順番で全然違う結果になってしまう。
回転が先か、移動が先かで全く違う結果になる!
深度テスト
深度テストは、奥行き情報を格納した深度バッファの値をテストしその結果に応じてレンダリングすること。
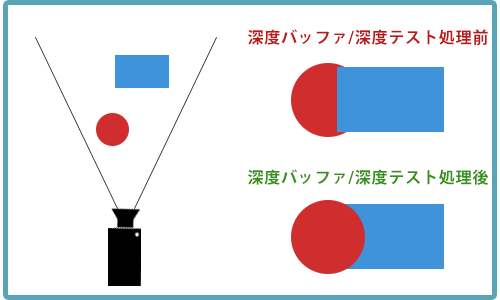
手前にあるものが奥にあるものを覆い隠すという表現をすることができる。
反対に深度テストを行わないと、 奥にあるもが手前にあるものを覆い隠してしまう。
WebGLは常に上書きモード
WebGLでは、ドローコールが実行されレンダリングが開始されると、 すべて無条件で上書きモード で描画される。つまり、奥のものが先に描かれ、手前のものが後に描かれれば問題ない。逆の場合は、その順番通りに描画されてしまうため、破綻してしまいます。
それを回避できるのが、深度バッファと深度テスト
深度バッファと深度テスト
深度バッファは、フレームバッファに含まれるバッファのうちの一つ。
奥行きに関する情報を扱う場合に使う。深度専用のバッファのため浮動少数点数の精度がとても高い。
深度テストは、深度バッファの値から描画すべきオブジェクトかどうか判断する。
描画しようとしているデータが、手前のオブジェクトに隠れるオブジェクトだった場合、隠れるオブジェクトは描画しない。という判断をしてくれる。
深度テストを有効かするには、gl.enable()メソッドを使用する。
// 引数にgl.DEPTH_TESTを与えると有効化される
gl.enable(gl.DEPTH_TEST);
深度テストの方法を決める
深度テストを有効化したらどのような基準でテストを行うかを設定する。
設定には、depthFuncメソッドを使う。
引数にgl.LEQUALを指定することで、手前のものに奥のものが隠れる表現ができる
gl.depthFunc(gl.LEQUAL);
カリング(陰面消去)
カリングは、カメラから見て隠れている部分を消してくれる。
無駄な描画が行われなくなるので、 パフォーマンスの向上 に繋がる!
ポリゴンの表と裏
カリングは厳密には、 ポリゴンの裏を描画しない機能 です。そのため、ポリゴンの表と裏をしっかりと理解して、計画的に使う必要があります。
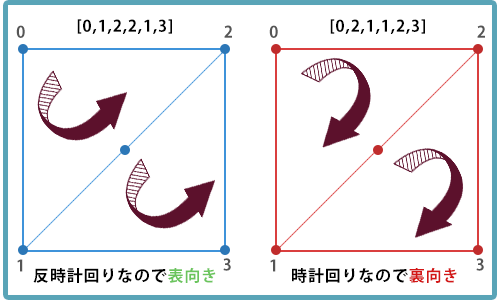
ポリゴンの表向きか裏向きかは 頂点の配置順 で決まり、頂点の配置順が、反時計回りが表で、時計回りが裏です。
クォータニオン
クォータニオンとは、行列と同じように数学の概念で 四元数 とも呼ばれます。
クォータニオンも行列と同じく理解するのはかなり大変なので、まずは使い方から覚える!
メリット
クォータニオンを使うと何がいいのか。クォータニオンは単体で 4つのデータ で構成されているため、行列よりも効率の良い。特に回転を扱うことに長けている。
行列で回転を行う場合の問題点を、クォータニオンなら解消できる。
クォータニオンは 回転を扱うスペシャリスト!
とはいえ、いきなり扱うのは難しいようなので、行列に慣れてきたらクォータニオンを使うほうが良いようです。
まとめ
- 行列自体を理解せずに、WebGLでの使い方をまず覚える
- 行列にはいくつか種類がある。なかでも以下の4種類はしっかりと理解しておく
- 正方行列
- 単位行列
- 転置行列
- 逆行列
- 行列は 掛ける順番 がとても重要
- 座標変換の流れをつかむ
- ローカル座標系(素のモデルデータ)
- モデル座標系(どの位置にどのように配置するか)
- ビュー座標系(カメラの位置、向き、上向き)
- プロジェクション座標系(三次元から二次元への変換)
- 座標系から座標系の遷移には行列が必要
- アプリケーションからシェーダに座標系を送る際は全てを掛け合わせる
- モデル座標系は 掛け合わせる順番 に注意する
- 深度テストを有効にするには
gl.enable()メソッドを使う。 - 深度テストを行うことで、奥にあるものが自然と隠れる
- カリングは見えない部分を除去する機能
- クォータニオンは回転のスペシャリスト
感想
今回は、行列について今までよりも深く学びました。
行列自体の理解はまだまだですが、正方行列、単位行列、転置行列、逆行列の4種類の行列はしっかり覚えておこうと思います。
モデル座標系の掛ける順番が違うと全く違う結果になってしまうことや、ポリゴンの表向きと裏向きの概念は、ちゃんと理解しておかないとこの先困ることになりそうです。
次回はラジアンとベクトリがメインな回になるそうです。ラジアンは大丈夫そうですが、ベクトルの方は不安しかないので、復習必須です。
続き
第五回 WebGLスクール 「ライティングの基本」
第六回 WebGLスクール 「テクスチャで画像データを使用する」
第七回 WebGLスクール 「ブレンドファクターとアルファブレンディング」
第八回 WebGLスクール 「シェーダエフェクトテクニック」
第十回 WebGLスクール 「ポストエフェクトテクニック」
第十一回 WebGLスクール「キューブ環境マッピング」