wgld.orgの管理人であるdoxasさん主催のWebGLスクールの第五回目です。
今回はランティング(照明効果)と回転アニメーションをモデルに適応する内容でした。
モデルに影が出てくるとすごく楽しくなってきます。
前回までのまとめ
第一回 WebGLスクール 「WebGLの概念」
第二回 WebGLスクール 「WebGLの手続きと手順」
第三回 WebGLスクール 「シェーダの基礎」
第四回 WebGLスクール 「行列とクォータニオンについて知る」
アニメーション処理
アニメーションの基本は、事前準備とアニメーションフレームに分ける。
準備とアニメーション関数を分離し、アニメーション関数を再帰的に呼び出す処理を行う。実際のコードでは、requestAnimationFrameを使用する。
function render(){
// フラグをチェックしてアニメーション
if(run){requestAnimationFrame(render);}
}
requestAnimationFrameについては以下を参照
ラジアンの算出と回転行列の生成
ラジアンとは弧度法のことです。今回はモデルをに回転アニメーションを適用させるので、ラジアンは欠かせません。
算出方法は以下になります。
ラジアン = 度数 * Math.PI / 180
回転行列生成ポイント
- カウンタから正しくラジアンを算出する
- モデル座標変換行列を最初い初期化する
- 回転がどの軸を中心に起こるかをイメージ
ライティングの基本
ライティングは完全に再現しようとすると計算量が多すぎて処理できない。 「それらしく見える」 が大事。
まずは、どう計算したらどういった結果が出るのかを理解する。
影の演出と光源の種類
ライティングによる影の有無で大分見た目が変わってきます。
また、光源にはいろいろな種類があり、光源によって見た目も変わってきます。実装時の考え方は基本的には同じ。3Dプログラミングにおける代表的な光源は以下の3つです。
- 平行光源
- 点光源
- スポットライト
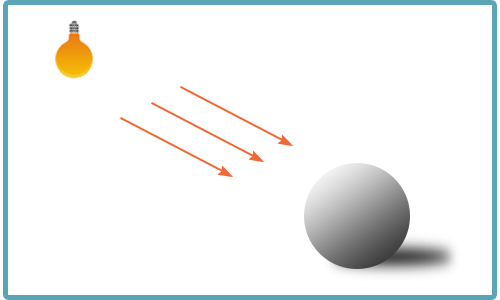
平行光源
光の筋が直線的で、すべての光線が平行になっている光源。
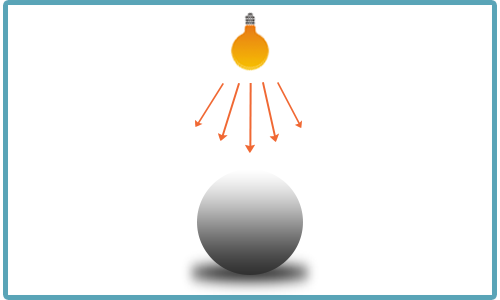
点光源
ある一点を中心に放射線状に放たれる光源。
スポットライト
円錐状に照らされる光源。
照明効果の種類
光源の種類は大きく分けて3種類の光源がありました。それとは別に光の、ライティングではモデルに影響を与える 光の照明効果の違い を知っておく必要があります。
光源が光の放ち方で、照明効果というのは光をモデルにどのように当てるかといもの。
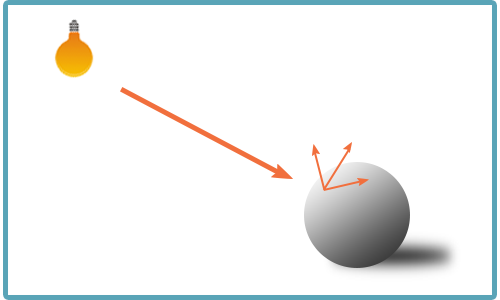
- 拡散光
- 環境光
- 反射光
拡散光
拡散光はモデルに光が当たり、拡散して広がっていく光を表現する。
環境光
環境光は壁などに反射しながら、環境全体に広がる光を表現する。
厳密に再現するものはとても大変。
反射光
反射光はモデルに光が反射し、レーザーのような光を強い光を表現する。
拡散光が光が散らばっていたのに対し、反射光は光が散らばらないのが特徴。
ライティングに必要なもの
1.頂点法線
頂点属性に頂点の法線を追加する。
頂点の法線とは、頂点それぞれは持っている 頂点の向き のこと。
頂点法線は、頂点が形成するポリゴンの向きを表す指標になり、光に対して垂直に立てるようにしたほうが強く当たるようになる。
面や頂点の向き は光の表現においてとても重要。
頂点法線用のattribute変数
頂点法線を指定するには、頂点シェーダに法線用のattribute変数を追加します。
attribute vec3 normal;
法線は一般的にnormalと表現され、向きを表すのでvec3と宣言する。
修正手順は以下
- ロケーションとストライドの準備
- VBOの生成と登録
- IBOの生成と登録
2.逆行列
ライティングには、 モデル座標変換行列の逆行列 が必要。
3.ライトベクトル
ライトベクトルは、平行光源から放たれた向きを表すもの。
逆行列とライトベクトルはuniformを追加し、シェーダに情報を送る。
逆行列は、4×4の正方行列を使い、ライトベクトルは、三次元ベクトルなのでvec3を使う。
uniform mat4 invMatrix;
uniform vec3 lightDirection;
javascript側でuniform関連の準備
uniformロケーションや、シェーダに送るデータを生成する。
uniformロケーションの取得
var uniLocation = [];
uniLocation[0] = gl.getUniformLocation(prg, 'mvpMatrix');
uniLocation[1] = gl.getUniformLocation(prg, 'invMatrix');
uniLocation[2] = gl.getUniformLocation(prg, 'lightDirection');
ライトベクトルの準備
var lightDirection = [0.577, 0.577, 0.577];
レンダリング関数の中で逆行列を求める
m.identity(mMatrix);
m.rotate(mMatrix, rad, [0.0, 1.0, 1.0], mMatrix);
m.multiply(vpMatrix, mMatrix, mvpMatrix);
// あらかじめ invMatrix を初期化しておく
m.inverse(mMatrix, invMatrix);
uniform系メソッドでシェーダに送る
gl.uniformMatrix4fv(uniLocation[0], false, mvpMatrix);
gl.uniformMatrix4fv(uniLocation[1], false, invMatrix);
gl.uniform3fv(uniLocation[2], lightDirection);
平行光源を数字で表現
平行光源は、無限に遠い場所から一直線に降り注ぐ光なので、向きがまったく同じと考える。つまり、光の向きを表すベクトルを1つ用意してあげればいい。
ライトベクトルと正規化
ライトベクトルは光の向きを表現するベクトル。
ライトベクトルで重要なのは、方向だけなので正規化しておく。
逆行列への理解
ポイントは、逆行列が モデル座標変換行列の逆行列 ということ。
モデル座標変換とは
レンダリングされるモデルをどんな位置、どんな姿勢、どんな拡大縮小を適応するのかを示した状態。
モデル座標系で、 空間上のどこにどのように配置されるかが決まる。
まずは、コードを見てみる。
vec3 inverseLight = normalize(invMatrix * vec4(lightDirection, 1.0)).xyz;
上記のコードでは、逆行列とライトベクトルとを掛け合わせ変換を行っている。normalizeは初期化用のビルトイン関数。
逆行列とはなんだったかを思い出す
逆行列とは
たとえば行列 A と行列 B を掛け合わせ、行列 C ができるとする。このとき行列 C に、行列 B' を掛け合わせると、計算結果が行列 A に戻るとする。
この行列 B' こそが逆行列で、言葉で表すなら「行列 B' は、行列 B の逆行列である」と言える。
つまり逆行列とは、ある行列の影響を そっくりそのまま打ち消してしまう行列 ということ。
モデル変換行列は、移動や回転などを行う行列だったのに対し、逆行列はある行列の影響を打ち消すものです。 つまり 元に戻る ということ。
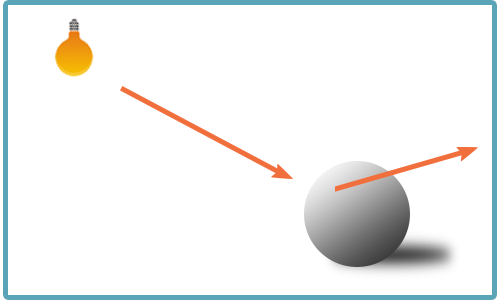
例えば以下の図のような関係性のモデルがあったとします。
これを反時計回りに90度回転させると・・・
右側からライトベクトル(光)が当たり、回転後も右側から放たれなければならないが、ライトベクトルも回転してしまっているために正しくライティングの計算が出来ていない。
そこでライティングに逆行列を掛けて、正しい位置に戻します。
照度について
光の向きについて学んだので、次は光の当たり具合を見ていきます。
今回の講座では、拡散光を表現していきます。
拡散光は、逆行列を適用したライトベクトルと、頂点の持つ法線の情報を用いて計算します。
一般的に拡散光は、 ディフェーズ(diffuse) と表現されます。
求め方から見てみる。
float diff = clamp(dot(inverseLight, normal), 0.1, 1.0);
上記のコードでは、GLSLビルトイン関数のdotのを使い内積(ドット積)を求め、同じくビルトイン関数のclampを使いクランプしています。
内積とは
内積はドット積をも呼ばれる数学の計算方法。
次元の同じベクトル同士は内積を取ることができる。内積については、追い追い理解しようと思う。
内積結果をクランプ
内積の計算結果は負の数値になることが多く、そのまま利用すると不都合が多い。
そのため、clamp関数を用いて一定の範囲内に数値を収める。
頂点かフラグメントシェーダか
今までの処理はほどんど頂点シェーダで行ってきましたが、フラグメントシェーダ側でもできる。
頂点シェーダは文字通り頂点に対して処理を適用する一方、フラグメントシェーダは全ての描画範囲のピクセルに対して実行される。つまり、フラグメントシェーダで処理するほうが高品質。しかし、フラグメントシェーダのほうが圧倒的に実行回数が多いので負荷も高くなる。
感想
今回は、光の種類や光の当て方について学びました。中でもライティングにおける逆行列の使い方を理解できたのは良かった。
そろそろ自分で何か作ってみたいなー。
次回は、光に関する内容で反射光や環境光についての講座になるそうです。
続き
第六回 WebGLスクール 「テクスチャで画像データを使用する」
第七回 WebGLスクール 「ブレンドファクターとアルファブレンディング」
第八回 WebGLスクール 「シェーダエフェクトテクニック」
第十回 WebGLスクール 「ポストエフェクトテクニック」
第十一回 WebGLスクール「キューブ環境マッピング」