概要
皆さんお酒は好きですか? 私は大好きです。
カクテルを頼むことも多いのですが、いつも同じのばかりを注文してしまいます。
もっといろんなカクテルを飲んでみたい・・・。
でも名前だけじゃどんなのかわからない・・・。
飲み慣れた酒と同じようなカクテルから試したい・・・。
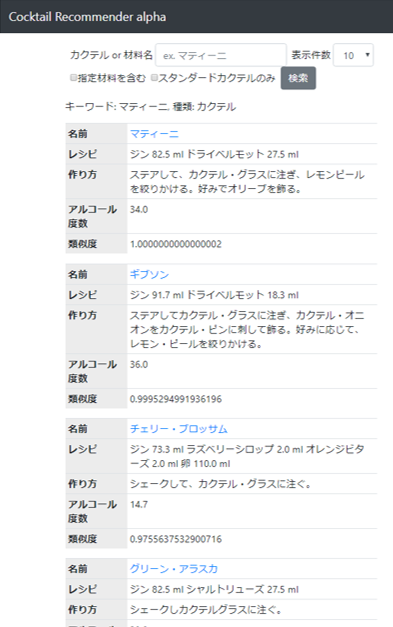
そんなわけで、カクテルの名前を入力すると、類似したカクテルの名前とレシピを検索してくれるアプリを作りました。
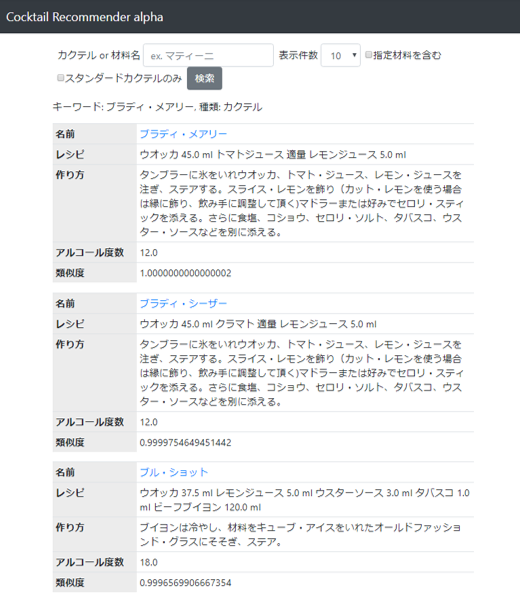
例えば、ブラディ・メアリー(ウオッカ+トマトジュース)で検索すると、
トマトジュースをクラマト(ホタテエキスの入ったトマトジュース)に変えたブラディ・シーザーや、同じくウオッカベースでスープ系カクテルのブル・ショットが類似カクテルとして抽出されます。
本記事では、この検索システムの核となる「カクテルのベクトル表現」に関して解説します。
アプリの作り方やスクレイピングのやり方に関してはまた後日……。
もくじ
カクテルとは?
カクテルの特徴量
カクテルレシピのスクレイピング
レシピの分散表現
作製技法+スタイルの分散表現
カクテルの分散表現を計算する
類似度の計算方法
まとめ
カクテルとは?
カクテル(英: cocktail)とは、ベース(基酒)となる酒に、他の酒またはジュースなどを混ぜて作るアルコール飲料のこと。(wikipediaより)
カクテルとは「2種類以上の酒類やジュース等の材料を混ぜて作るドリンク」のことです。
カクテルの種類は名前が知られているものだけで数千種以上は存在します。
例えば、CDB - カクテルデータベースには現在10,000種以上のカクテルが収録されています。
今回は、こちらのサイトからデータをお借りして類似度の計算を行っていきます。
カクテルの特徴量
カクテルを特徴づける変数には、以下の3つがあります。
- レシピ
- 作製技法(ビルド, ステア, シェーク, ブレンド)
- スタイル(ショート, ロング, ホット, トロピカル)
作製技法は材料の混合方法、スタイルはカクテルの提供される形式です。
この3つの変数を用いることで、例えば、マティーニというカクテルは以下のように表されます。
マティーニ
レシピ: ジン 82.5 ml, ドライベルモット 27.5 ml
作製技法: ステア
スタイル:ショートカクテル
カクテル間の類似度を判定するためには、これら特徴量の分散表現(ベクトル)を得る必要があります。
今回は、自然言語処理の手法を用いたカクテルのベクトル化を目的としていきます。
カクテルレシピのスクレイピング
Webページのスクレイピングには、標準ライブラリのurllib.requestとbeautifulsoup4を使いました。
データベースからのスクレイピングに関しては、この記事では詳しく取り扱いません。
(要望があればそのうち書きます)
各カクテルに関して、CDBからスクレイピングした次のようなデータを解析に用いました。
ちなみに、カクテルレシピの総数は11013です。
dataset = [{'jpname': 'マティーニ',
'enname': 'Martini',
'base': 'Gin',
'style': 'Short',
'make': 'Stir',
'ABV': 34.0,
'recipe': [['ジン', 82.5], ['ドライ・ベルモット', 27.5]],
'Howto': 'ステアして、カクテル・グラスに注ぎ、レモンピールを絞りかける。好みでオリーブを飾る。'}
...]
レシピの分散表現
自然言語処理の分野では、単語の分散表現(ベクトル)から文書のベクトルを求めるということがよく行われます。
今回の場合に当てはめれば、文書=カクテル、単語=材料ということになります。
そこで、材料のベクトルを得てから、それの重み付き平均化でカクテルの分散表現を求めることを目的とします。
まず、材料のベクトルを得るために、その共起関係の行列を作成します。
一例として、カクテルのデータセットが[ホワイトレディ, サイドカー, X.Y.Z., バラライカ]であるとします。
このデータセットに用いられるすべての材料を羅列すると、[ジン, ブランデー, ラム, ウオッカ, コアントロー, レモンジュース]となり、共起関係行列は次のようになります。
names = ['ジン','ブランデー','ラム', 'ウオッカ', 'コアントロー', 'レモンジュース']
dataset=[[0,0,0,0,1,1], # <=ジン
[0,0,0,0,1,1], # <=ブランデー
[0,0,0,0,1,1], # <=ラム
[0,0,0,0,1,1], # <=ウオッカ
[1,1,1,1,0,4], # <=コアントロー
[1,1,1,1,4,0]] # <=レモンジュース
この行列をPCA(主成分分析)を用いて2次元まで次元削減して可視化してみましょう。
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
# PCAで変換
pca = PCA()
pca.fit(dataset)
r_dataset = pca.fit_transform(dataset)
# 第1,2成分でプロット
fig = plt.figure(figsize=(5,5))
for n,i in enumerate(names):
plt.scatter(r_dataset[n,0],r_dataset[n,1], s=10)
plt.text(r_dataset[n,0],r_dataset[n,1], i)
plt.xlim(-3.2,4.5)
カクテルベースとして同じような使われ方をされるジン, ブランデー, ラム, ウォッカが近い位置に存在することがわかります。
このように、共起関係行列を用いることで、材料の使われ方に対応した分散表現を得ることができます。
さて、今回の全レシピに含まれる材料の総数は1256種類なので、共起関係は(1256,1256)次元の行列となります。
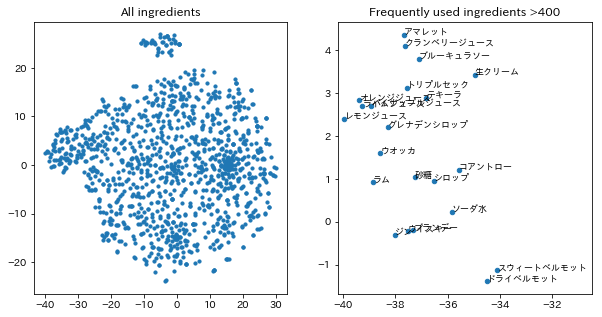
この行列をPCAで(1256,100)まで、さらにt-SNEにより(1256,2)まで削減したプロットは下のようになります。
左が全材料のプロット、右が400回以上用いられた材料のみのプロットになります。
ベースリカー、ジュース類、リキュール類、ベルモット等がまとまっているように見えますね!
とりあえず、これでカクテル材料の分散表現を100次元のベクトルとして得ることができました。
作製技法+スタイルの分散表現
さらに、カクテル分類のためには作製技法とスタイルの分散表現も必要です。
作製技法(4種)、スタイル(4種)はカクテルごとに決まっているために8次元のOne-hotベクトルとして表現することができます。
例えば、先に述べたマティーニのレシピであれば、
['ビルド','ステア','シェーク','ブレンド','ショート','ロング','ホット','トロピカル'] = [0,1,0,0,1,0,0,0]
と表すことができます。
全カクテル(11013個)のベクトルを結合すると(11013,8)の行列となります。
各材料の表現をを2次元のベクトルに圧縮するために、今回は特異値分解(SVD)を用います。
styles_list = ['Short', 'Long', 'Hot', 'Tropical', 'Build', 'Shake', 'Stir', 'Blend']
matrices = []
# (8,11013)次元の行列を作製
for n,i in enumerate(dataset):
matrix = np.zeros(len(styles_list))
for m,j in enumerate(styles):
matrix[styles_list.index(i[j])] = 1
matrices.append(matrices)
matrices = np.array(matrix)
matrices, s, V = np.linalg.svd(matrices, full_matrices=True)
matrices = matrices[:,:2]
SVDを用いた次元削減に関しては、以下の記事を参考にしました。
SVD(特異値分解)解説
2次元に圧縮したベクトルを可視化すると、以下のようになります。
(作製技法(make)およびスタイル(style)によって4種に色分けされています)
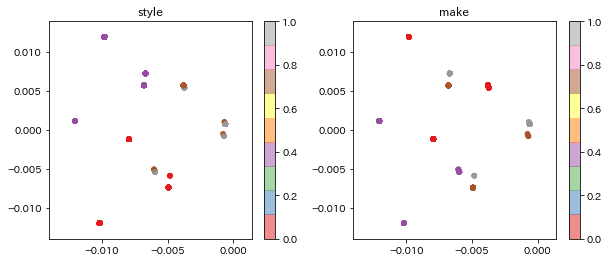
カクテルのスタイル、および作製技法によってベクトルが分かれていることが分かります。
次からは、この2次元のベクトルとレシピを組み合わせて、カクテルの分散表現を求めていきます
カクテルの分散表現を計算する
一例として、先に例として示したマティーニの場合を考えます。
まず、材料の使用割合を重みとしてベクトルを足し合わせます。つまり、マティーニの場合は
マティーニ = ジン×3/4 + ドライ・ベルモット×1/4
となります。
これでレシピだけを考慮したカクテルのベクトル(100次元)を得ることができます。
さらに、スタイル+作製技法に対応した2次元のベクトルを掛け合わせて200次元のベクトルにします(この操作をどう言ったらいいのかわからない……)。具体的には次のような操作をしています。
# gin, dry_vermouthは100次元の材料ベクトル
# style_makeは2次元の作製技法+スタイルのベクトル
martini = gin * 3/4 + dry_vermouth * 1/4
martini = np.hstack((martini*style_make[0], martini*style_make[1]))
これでようやくカクテルの分散表現が得られました!
早速、このベクトルをt-SNEで2次元まで削減して可視化してみましょう。
各点がそれぞれのカクテルを表しており、プロット間の距離はカクテルの類似度を表現しています。
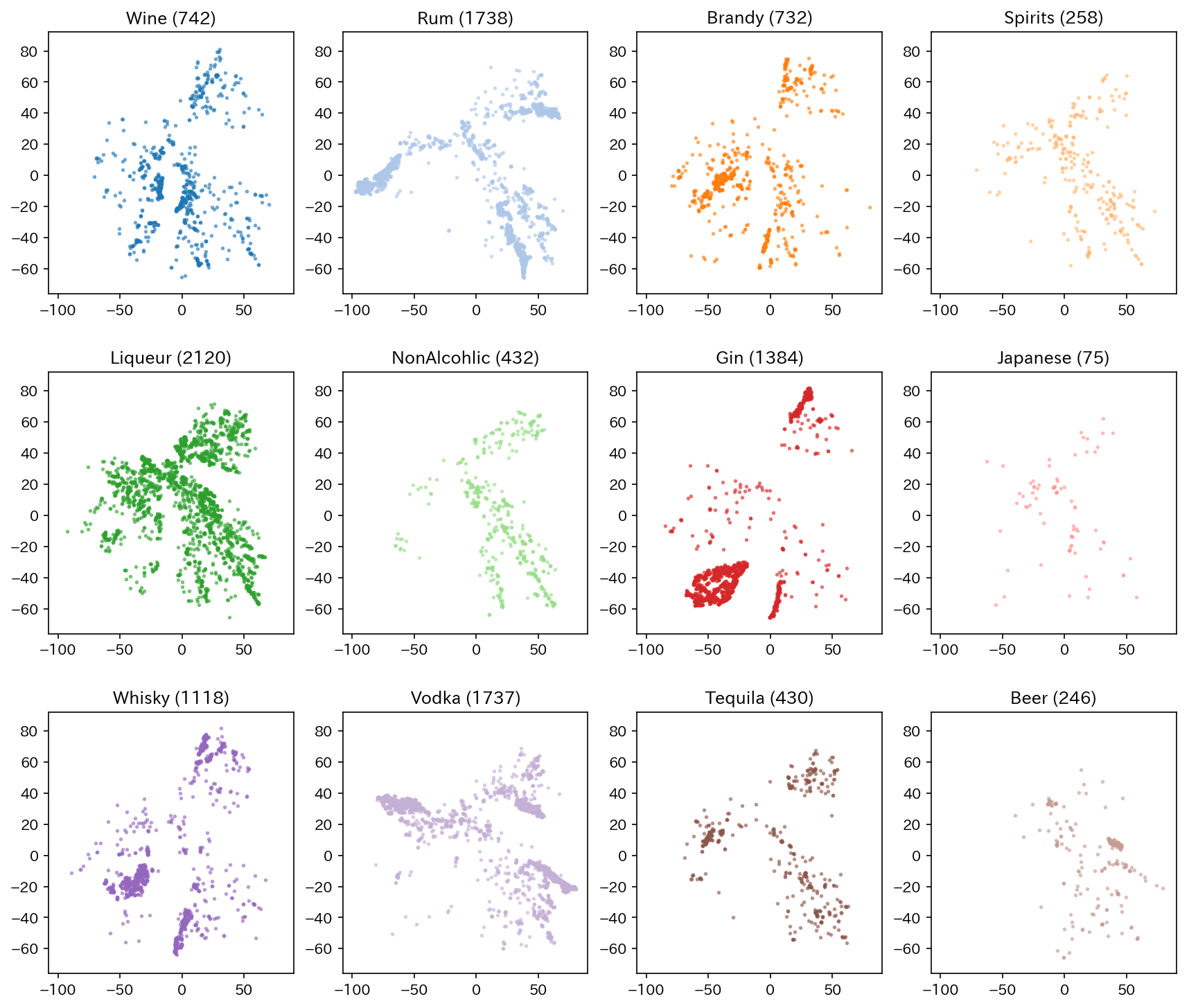
また、プロットの色はベースとなる酒類を表しています。分けてプロットすると以下の通り。
結構きれいにクラスターが分かれていますね。
ジン,ウォッカ,ラム等は特に顕著です。逆に、リキュールベースやノンアルコールカクテルは比較的広い分布を持っているように見えます。
類似度の計算方法
ベクトルが得られたので、コサイン類似度で類似カクテルの検索を行ってみます。
類似度の検索にはコサイン類似度を用いています。
def cos_sim(v1, v2):
s = np.dot(v1, v2) / ((np.linalg.norm(v1) * np.linalg.norm(v2)) + 1e-9)
return s
類似カクテルを検索してみる
ほとんど同じレシピで作り方が微妙に違うカクテルが多いので、なかなかうまく検索できません。
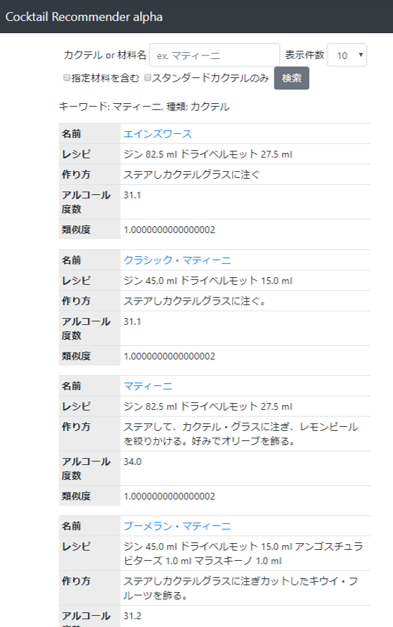
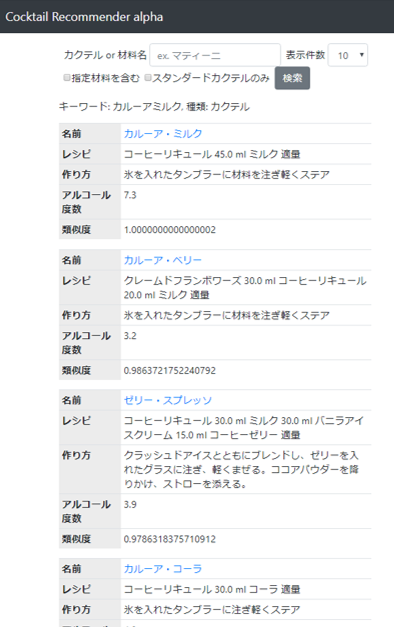
そんな時はスタンダードカクテルのみで検索してみましょう。
すると、ジンベースのギブソンやチェリーブロッサム、グリーンアラスカ等が類似カクテルとして表示されます。
バーに行って頼むときは、スタンダードカクテルの中から選ぶのがいいかもしれません。ブーメランマティーニとか、たぶんバーテンダーさんもわからないので……。
カルーア・ベリーは美味しそう!
フランボワーズリキュールは比較的どこでも置いてあると思うので、レシピを見せれば作ってもらえそうです。
まとめ
もともとは自然言語処理の勉強をしてたんですが、これレシピにも使えるんじゃね? と思ってやってみました。
意外とうまくいきました。
ちなみに、アプリのプラットフォームにはHerokuを、フレームワークにはFlaskを使っています。
もともとhtmlを齧っていたのもあって、2日程度でできました。おススメです。
飲み屋で話のタネにでもなればなあと思ってます。
荒削りな部分も多いですが、改善点等あればお教え頂ければありがたいです。
それでは。