はじめに
今回はこんなのを作ります。
核生成を伴う相変態の数理モデルであるJMAK式のシミュレーションを行います。
これで君も材料工学研究者だ!
この記事の作成には、以下の文献を参考にしました。
相変化の速度論の系譜 Johnson-Mehl-Avramiの式をめぐって
相変化の速度論 —その発想と発展—
もくじ
JMAK式とは?
ある相Aが核生成を伴いながら相Bに変態していく場合における、
相Bの体積の時間変化を表す数理モデルのことです。
金属学の分野でJohnson, Mehlらが1938年に、
1939年にAvramiがそれぞれ独自に考案した数理モデルであり、
数学的な定式化を行ったロシアの数学者Kolmogolovも加えて、
Johnson-Mehl-Avrami-Kolmogolov(JMAK)式と呼ばれています。
JMAK式は現在より80年も前に考案されたものであり、
現在の計算材料科学の先駆けとなったモデルです。
かといって化石のように忘れ去られているかというとそうではなく、
現在でも様々な系に適用・改良が行われています。
JMAK式は教科書では必ず取り扱われているような重要な式なんですが、
なぜかシミュレーション例が見つからなかったので、作ってみました。
モデルの概要
ある相A(青色)が相B(赤色)に変化する過程を考えます。
図のように、相変態は一瞬で起きるわけではなく、核形成と共に段階的に進行します。
単純に考えれば、赤色の面積の変化を追えばいいだけに思いますが、
結晶核はいずれ衝突するので、どのように数式として取り扱うのかが問題となります。
そこで、JMAKモデルでは「核が衝突しても成長を続ける」と仮定します。
すると当然重なり合う部分が出てくるわけですが、
重複を含めた部分の面積(体積)は拡張体積$V_{ex}$と置いておきます。
ここで、さらに「すでに核が生じている部分でも核生成が起きる」と仮定すると、
相Bの総体積$V$と拡張体積$V_{ex}$の間に以下の関係が成り立ちます。
V = 1 -exp(-V_{ex})
$V_{ex}$の時間変化は簡単に計算することができ、例えば3次元の場合$t$の4乗に比例します。
これを一般的に表した以下の式がJMAK式と呼ばれます。
V = 1 - exp(-kt^n)
$k, n$は核生成頻度と核の形状、次元によって変化する定数です。
今回はシミュレーションでこの等式が成り立つことを示してみたいと思います。
シミュレーションの概要
JMAKモデルのPythonによるコードは以下のようになります。
行列計算にnumpy、可視化にmatplotlibとseabornを用いました。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import random
# シミュレーション条件の定義
steps = 80 #計算ステップ数
delta_t = 1 #タイムステップの幅
grid = 100 #計算グリッドの大きさ
nuc_rate = 1.0E-7 #核生成頻度
growth_rate = 0.4 #結晶核の成長速度
initial_size = 1.0 #結晶核の初期サイズ
# 計算範囲内のグリッドを作成
x = np.linspace(0, grid-1, grid)
y = np.linspace(0, grid-1, grid)
xx, yy = np.meshgrid(x,y)
# 配列の定義
pos_nuc = [] #結晶核の位置
r_nuc = [] #結晶核のサイズ
V_sum = [] #相変換面積の総和
V_eff = [] #拡張面積の総和
# ここから計算
no_nuclei_flag = True #核が領域内に存在しないかを判定するフラグ
for i in tqdm(range(steps)):
num_nuc = nuc_rate * (grid*grid) * delta_t #タイムステップの間に生成する核の総数
p_nuc = (num_nuc - int(num_nuc)) #核が生成する確率
dt_growth_rate = growth_rate * delta_t #成長による結晶核の半径の変化
#既に存在する核の半径をdt_growth_rateだけ増加させる。
if(i != 0):
for j in range(len(r_nuc)):
r_nuc[j] = r_nuc[j] + dt_growth_rate
# num_nucの小数点以下の値で、核が生成するかを判定する
# num_nucが1以下になるような条件でも、核が生成できるようにするため。
if(random.random() > p_nuc):
num_nuc = int(num_nuc) + 1
#num_nucの数だけランダムに核を生成する。
#また、核の中心からの距離を行列としてdistanceに保存する。
if(num_nuc >= 1):
for j in range(num_nuc):
x_nuc = random.randint(0,grid)
y_nuc = random.randint(0,grid)
pos_nuc.append([x_nuc, y_nuc]) #核の位置を保存
r_nuc.append(initial_size) #核の半径を初期値に設定
distance = np.sqrt((xx - x_nuc)**2 + (yy - y_nuc)**2) #核からの距離を行列に保存
if(no_nuclei_flag):
distance_fields = [distance]
no_nuclei_flag = False
else:
distance_fields = np.append(distance_fields, [distance], axis=0)
#核が1つでも存在する場合、変換体積V_sumと拡張体積Veffを計算
if(len(r_nuc) != 0):
#それぞれの結晶核に対する距離行列を求める。
for j in range(len(distance_fields)):
temp = np.where(distance_fields[j]<r_nuc[j], 1, 0)
if(j == 0):
nuc_fields = [temp]
else:
nuc_fields = np.append(nuc_fields, [temp], axis=0)
#拡張体積の行列を計算
if(len(r_nuc) > 1):
Veff = nuc_fields.sum(axis=0)
else:
Veff = nuc_fields[0]
V = np.where(Veff >= 1, 1,0) #変換体積の行列を計算。Veffのうち1以上の部分を1とする。
V_sum.append(V.sum()/(grid*grid)) #このタイムステップでの変換体積の総和を保存。
V_eff.append(1 - np.exp(-1 * Veff.sum()/(grid*grid))) #拡張体積の総和を保存。
#各ステップごとにプロットを保存
fig = plt.figure(figsize=(10,4))
#変換体積をヒートマップでプロット
plt.subplot(1,2,1)
plt.title("step"+str(i))
sns.heatmap(V, square=True, vmin=0, vmax=1, cmap='coolwarm', yticklabels=10, xticklabels=10, cbar=True)
#拡張体積をヒートマップでプロット
plt.subplot(1,2,2)
plt.title("step"+str(i))
sns.heatmap(Veff, square=True, vmin=0, vmax=20, cmap='coolwarm', yticklabels=10, xticklabels=10, cbar=True)
plt.savefig("step"+str(i)+".png")
plt.close()
プログラムの簡単な説明
以上のプログラムの計算の流れを簡単に説明すると、以下のようになります。
- 既に存在する結晶核の半径をgrowth_rate*delta_tだけ増加させる。
- 核生成頻度を計算し、その分だけ結晶核をランダムな位置に加える。
- それぞれの結晶核からの距離マップを作成する。
- 距離マップの結晶核のサイズ$r$より大きい領域を0に、小さい領域を1に2値化する。
- 4で作成した2値行列を重ね合わせ、拡張体積$V_{ex}$の行列を作成する。
- $V_{ex}$の行列を1を閾値に2値化して、変換体積$V$の行列を作成する。
- 1~6を任意のステップ数繰り返す。
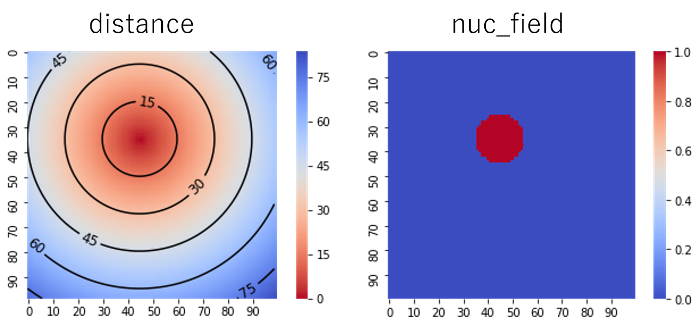
ここで言う距離マップとは、結晶核中心からの距離を値として持つ行列のことです。
以下のように、距離マップ(distance)を結晶核のサイズを閾値に二値化し、
結晶の存在する領域の行列(nuc_field)を得ます。
(下図は$x=45$, $y=35$, $r=10$の結晶核です)
このnuc_fieldをすべての結晶核に対して計算し、足し合わせて拡張体積を得ます。
上のコードではこの距離を毎サイクル計算してしまっているので、けっこう遅いです。
その辺り改善の余地ありですが、そもそもそんなに重い計算でもないので……。
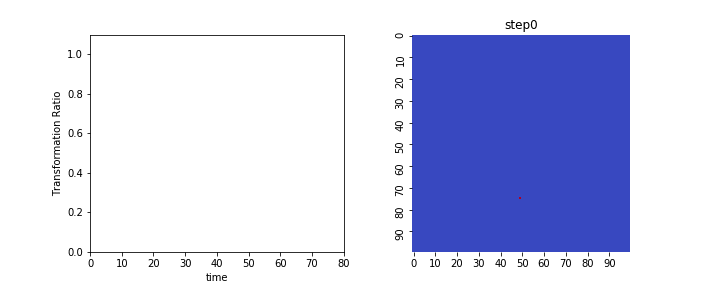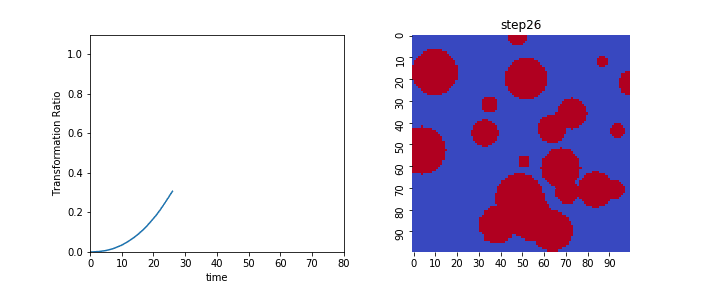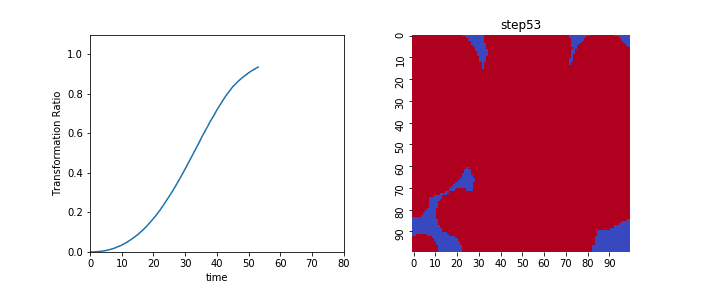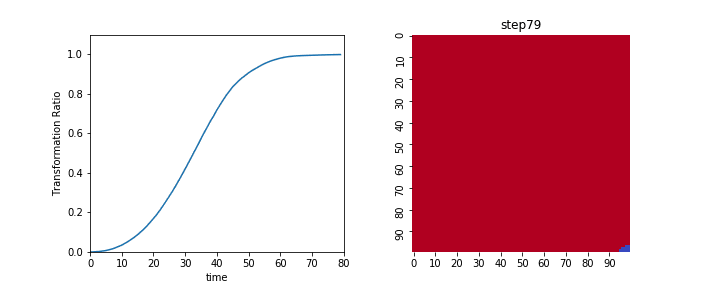
シミュレーション結果
上で説明したモデルをそのままシミュレーションし、
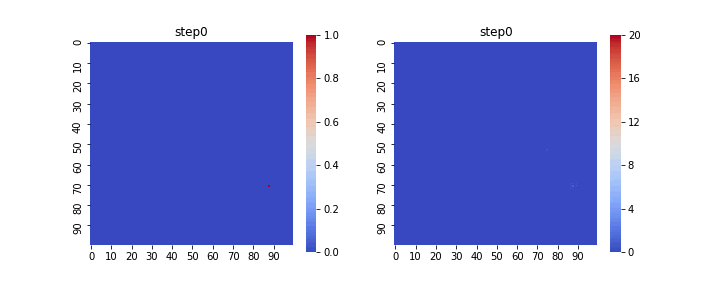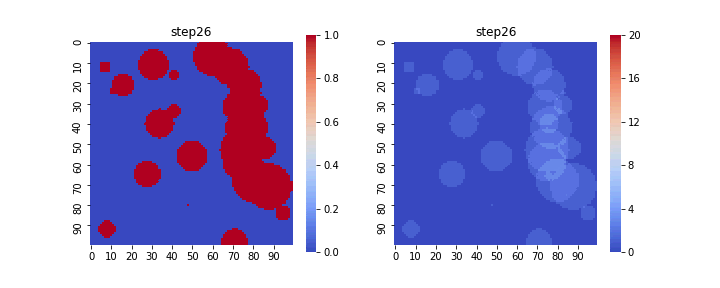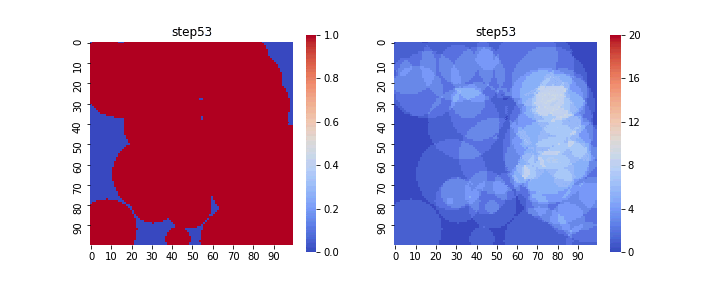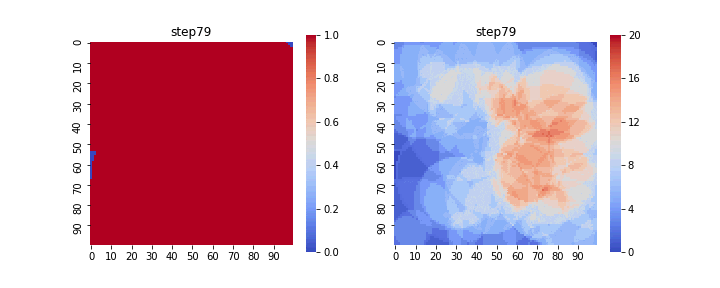
変換面積$V$と拡張体積$V_{ex}$の時間変化をアニメーションで表示すると以下のようになります。
左が変換体積$V$の変化で、結晶核が存在する領域が1、しない領域が0となっています。
右は拡張体積$V_{ex}$であり、結晶核が重なり合った面積が足しあわされている様子がわかります。
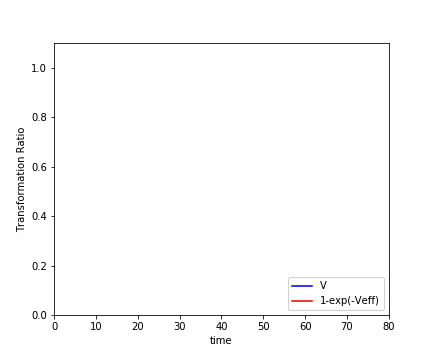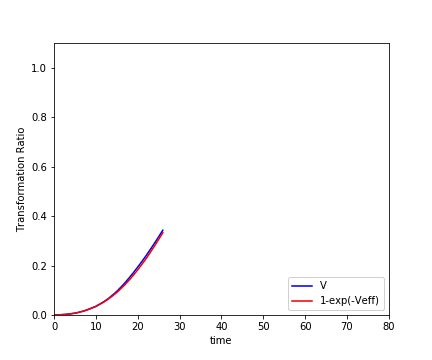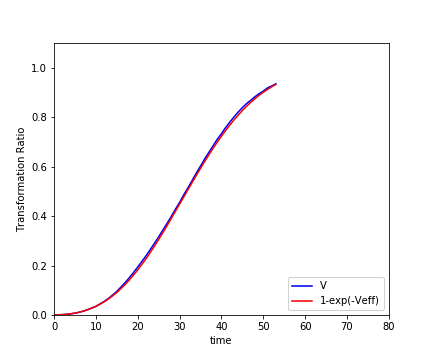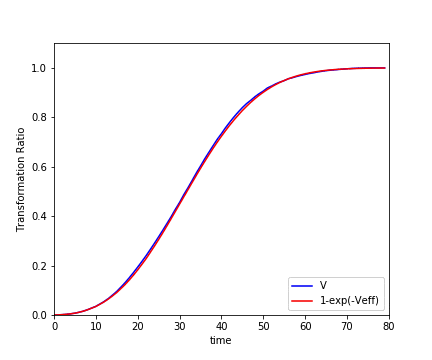
さて、それではJMAK式が正しいかどうかを確かめてみます。
各値を足し合わせ、変換体積$V$と$1 -exp(-V_{ex})$の時間変化をプロットします。
両者のプロットは確かによく合っていることが分かります。1
- 核が衝突しても成長を続ける
- すでに核が生じている部分でも核生成が起きる
以上の仮定をもとにすれば、$V=1 -exp(-V_{ex})$が成り立つことがわかりますね。
そもそもなぜこの式が成り立つのかということに関しては、
繰り返しになりますが、以下の文献が参考になります。
相変化の速度論の系譜 Johnson-Mehl-Avramiの式をめぐって
それでは最後に関数のフィッティングをやって終わりたいと思います。
JMAK式でのフィッティング
一般式である $V = 1 - exp(-kt^n)$ を使い、シミュレーション結果のフィッティングを行います。
フィッティングにはscikit-learnを使います。以下の記事を参考にしました。
コードはこんな感じです。
from scipy.optimize import curve_fit
def linear_fit(t, k, n): #JMAK式を定義
return 1 - np.exp(-1 * k * t ** n)
t = np.linspace(0, steps-1, steps)
param, cov = curve_fit(linear_fit, t, V_sum) #フィッティングを実行
fit = linear_fit(t, param[0], param[1]) #フィッティングの結果を出力
print(param[0], param[1]) #パラメーターk, nを表示
# フィッティング結果の描画と保存
plt.plot(V_sum ,lw=4, ls='dotted', label='simulation')
plt.plot(fit, label='fitting')
plt.xlabel('time')
plt.ylabel("Transformation Ratio")
plt.legend(loc='lower right')
plt.savefig("curvefit".png")
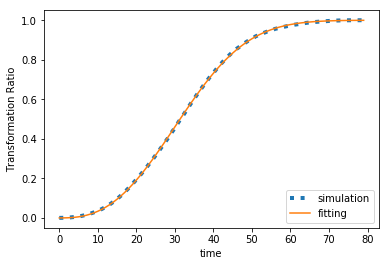
フィッティング結果は次のようになりました。よく合ってますね。
ちなみに$k=7.98284513×10^{-5}$, $n=2.63233243$となりました。
2次元の場合$n=3~2$になるとのことですが、その範囲に収まっています。
まとめ
以上、シミュレーションによるJMAK式の再現を行いました。
実はこの計算、以前にC++で書いたことがあったのですが、
数値計算やデータ処理を完全にPythonの方に乗り換えたので、書き直してみました。
やっぱりnumpyやmatplotlibは使いやすいですね~。もう戻れません。
材料工学関連のシミュレーションでは、イジング模型やフェーズフィールド法、
パーコレーションや拡散律速凝集(DLA)モデルなど、面白いのが多いので、
今後もいろいろとチャレンジしていきたいですね。
それでは~。
-
「一致している」なんて言うと怒られますね。実際に2つのプロットが完全に一致しないのは、JMAKモデルでは領域端の存在を考慮していないからでしょう。 ↩