Online Matching and Ad Allocation 勉強会: 第 7 章 Display Ads

はじめに

A. Mehta による Online Matching and Ad Allocation という書籍 (PDF) の輪読会の発表資料です。

このドキュメントは、第 7 章 Display Ads の解説になります。

Display Ads の問題設定

問題設定

• 頂点 $u$ と $v$ を結ぶ辺 $(u,v)$ には、重み $w_{uv}$ が存在する
• 頂点 $u$ にはキャパシティ $c_u$ が存在する
  • 頂点 $u$ とマッチングできる頂点 $v$ の個数は $c_u$ 個以下に制限される
• マッチング結果における、辺の重みの合計 $\sum w_{uv}$ を最大化したい

広告配信に置き換えると…

• インプレッション数保証型の広告配信 に近しい？
  • 限られたインプレッション数において、できるだけ成果を最大化したい
  • 成果: クリックやコンバージョンなど
• これに置き換えると
  • 頂点 $u$ は 広告 (キャンペーン) となる
  • 頂点 $v$ は インプレッション となる
  • 重み $w_{uv}$ はクリックやコンバージョンの有無 $\{0,1\}$ やクリック率 (CTR, click-through rate)、コンバージョン率 (CVR, conversion rate) に相当する？
  • キャパシティ $c_u$ は広告 $u$ に対するインプレッション数の上限相当する

Adversarial なモデル

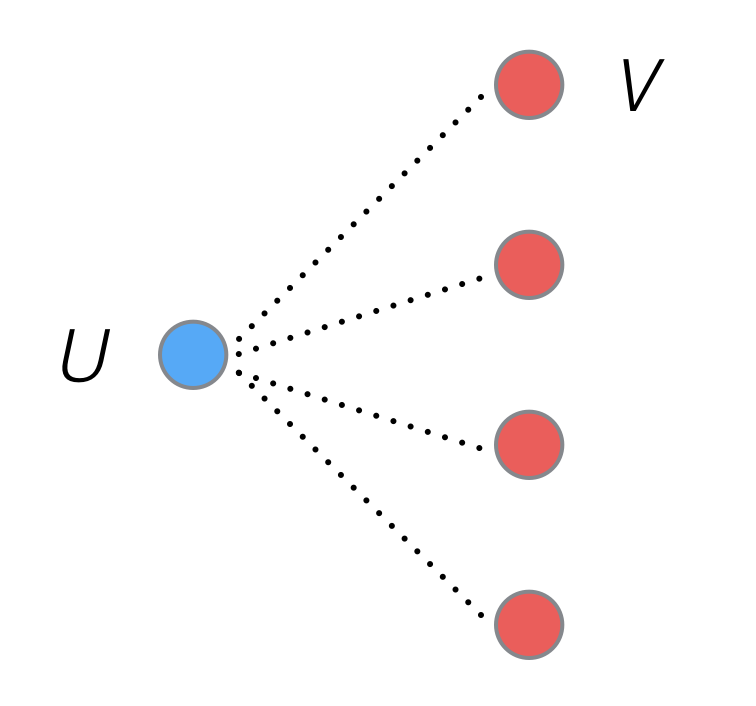
• Star graph を考える
  • 
  • 頂点 $u$ は一つだけ存在する
    • $|U| = 1$
  • 頂点 $v$ は複数存在する
  • すべての頂点 $v$ は、頂点 $u$ とマッチングできる
    • $(u,v) \in E$
  • 頂点 $u$ とマッチングできる頂点 $v$ は一つのみ
    • $c_u = 1$
• この Star graph における最適なマッチングを求める問題は 秘書問題 (Secretary problem) に相当する
• Adversarial なモデルでは、非自明な競合比を得ることができない
  • Random order なモデルについて先に考える
  • その後に Free-disposal モデルについて考える

7.1 Random Order and Secretary Algorithms

Classic Secretary

• まずは star graph = Classic Secretary に対するアルゴリズムから考える
• アルゴリズム
  • Phase 1:
    • 最初に到着する $|V| / e$ 個の頂点を無条件でリジェクトする
      • $u$ とはマッチングさせない
    • 上記でリジェクトした頂点 $v$ の $u$ との間の辺 $(u,v)$ の重み $w_{uv}$ について、その重みの最大値を $m$ とする
  • Phase 2:
    • Phase 1 で得た $m$ を超える重み $w_{uv}$ を持つ頂点 $v$ が最初に到着したところで $u$ とマッチングさせる
      • $m$ を超える頂点が到着しなかった場合 (= phase 1 でリジェクトした頂点に最適解が含まれている場合) は失敗とみなす
• このアルゴリズムの競合比は $1/e$ である
  • Phase 1 において、二番目に大きい重みを ($u$ との間の辺に) 持つ頂点が出現し、また phase 2 に一番大きい重みを持つ頂点が出現する確率が $\frac{1}{e} (1 - \frac{1}{e}) \simeq 0.23$ となる
  • 加えて、phase 1 において三番目に大きい重みの頂点が出現し、また phase 2 において、二番目に大きい重みの頂点よりも先に一番大きい重みの頂点が到着するケースなどを考慮すると、 $1/e$ となる

Secretary Matching

DP08, KP09

• 次に秘書問題を一般化したケース ($|U| \ge 1$) に対するアルゴリズム DP08, KP09 を考える
• アルゴリズム
  • Phase 1:
    • 最初に到着する頂点より、(全体に対する) 半分の個数の頂点をリジェクトする
      • リジェクトした頂点の集合を $V_1$ とする
    • $U$ と $V_1$ で構成されるグラフに対して、グリーディーに重みの最大化を図ったマッチング $\mathcal{M}_1$ を求める
    • マッチング結果 $\mathcal{M_1}$ において頂点 $u$ に着目し、その頂点とマッチングされた頂点 $v$ との間の辺の重みを $t_u$ とする
      • マッチングが存在しない頂点 $u$ の場合は $t_u = 0$ とする
  • Phase 2:
    • 到着した頂点 $v$ について、その $v$ と隣接する頂点 $u$ のうち、$w_{uv} \ge t_u$ の条件を満たすものの中から最大の重み $w_{uv}$ が得られる $u$ とマッチングさせる
• このアルゴリズムの競合比は少なくとも $1/8$ となる

KRTV13

• 前述のアルゴリズム DP08, KP09 よりも、よりよい競合比を達成するアルゴリズムを考える
• DP08, KP09 では、最初の半分の頂点をリジェクトして、重みに対するしきい値を事前に明示的に求めていた
• このアルゴリズム KRTV13 では、頂点が到着するごとに局所最適解を求め、その局所最適解に基いて
• アルゴリズム
  • 最初に到着する頂点より、(全体に対する) $1/e$ 個の頂点をリジェクトする
    • リジェクトした頂点の集合を $V'$ とする
  • マッチング結果の集合を $M = \emptyset$ とする
  • 次々に到着する頂点 $v$ について
    • $V' = V' \cup \{v\}$ とする
    • 現時点でのグラフ $G(U, V', E')$ より、局所最適なマッチング $M'$ を求める
    • 局所最適なマッチング結果 $M'$ において、$v$ と $u$ がマッチングされていて、かつ $u$ が $M$ において許容できる (？ キャパシティ的な意味、ということ？) 場合に、$(u,v)$ を $M$ に追加する
• (何というか、これは力技感がある…)
• このアルゴリズムの競合比は $1/e$ であり、これが最適である

7.2 Adversarial Order and the Free-Disposal Model

Free-Disposal モデルとは

• 端的にいうと、頂点 $u$ とマッチングできる頂点 $v$ の数を、キャパシティ $c_u$ 以上に緩和する、というもの
• ただし、キャパシティ $c_u$ を超えたマッチングした場合は、重みの高い順に $c_u$ 個のマッチングだけを目的関数の計算に利用する
• Free-Disposal モデルの目的関数は次のとおり

\sum_{u \in U} f_u(V_u)

• なお $f_u(V_u)$ は次の通り

f_u(V_u) = \max_{S \subseteq V_u, \ |S| \le c_u} \sum w_{uv}

• $V_u \subseteq V$ は、頂点 $u \in U$ とマッチングした頂点 $v \in V$ の集合を表す
• つまり $f_u(V_u)$ は、頂点 $u$ とマッチングした頂点 $v$ の集合 $V_u$ より、辺の重みが大きい順に $c_u$ 個の頂点を選んで、重みを合計したものに相当する
• 最初に考えた star graph のケースについては、この Free-Disposal モデルであれば、adversarial な順に頂点が到着しても競合比 1 を達成できる
• Free-Disposal モデルを導入する理由
  • Display Ads が想定しているインプレッション数保証型の広告配信において、保証された以上のインプレッションが生じる・得られることは、追加費用を支払う必要がない限り、広告主的には悪いことではない
    • (メディア側の立場で考えると、1 インプレッションあたりの単価が安くなってしまうわけなので、あまりうれしいことではない)

アルゴリズム

FKMMP09 のアルゴリズム

• 到着した頂点 $v$ について、 $w_{uv} - \beta_u$ が最大となる頂点 $u$ に割り当てる
  • $\beta_u$ は頂点 $u$ におけるビッドスケーリングルールを表す
  • 見てのとおり、(前章までのような) 乗算によるスケーリングではなく、加算・減算によるスケーリングをしている

ビッドスケーリングルール

• $V_u$ を、頂点 $u$ とマッチングした頂点 $v$ の集合とする
• $n_u$ を、頂点 $u$ とマッチングした頂点 $v$ の個数とする
  • つまり $n_u = |V_u|$
• $w_j$ を、集合 $V_u$ に含まれる頂点について、その重みの降順にソートしたときの $j$ 番目の頂点の重みとする

Greedy

\begin{eqnarray}
\beta_u = \left\{
\begin{array}{l}
0, & \rm if \ n_u < c_u \\
w_{c_u}, & \rm if \ n_u \ge c_u 
\end{array}
\right.
\end{eqnarray}

• Dispose が (= 頂点 $u$ のキャパシティ $c_u$ を超える) 生じるマッチングの場合に、 $\beta_u$ が 0 より大きな数値になる
  • $\beta_u$ は dispose されるマッチングの重みに相当する
• 競合比は $1/2$ となる

Exponential weighting scheme

\beta_u :=\frac{1}{n_u((1 + \frac{1}{n_u})^{n_u} - 1)}
\sum_{j = 1}^{n_u} w_j (1 + \frac{1}{n_u})^{j-1}

• キャパシティ $c_u$ がいずれも大きな値の場合、競合比は $1/2$ よりもよくなる
  • $c_u \rightarrow \infty, \forall u \in U$ のとき、競合比は $1 - 1/e$ を達成する