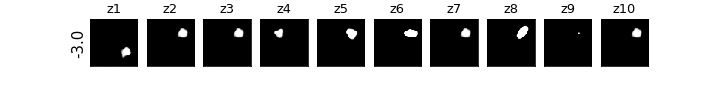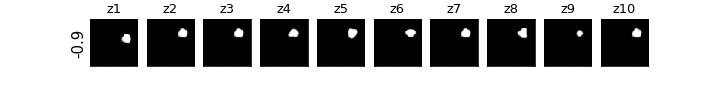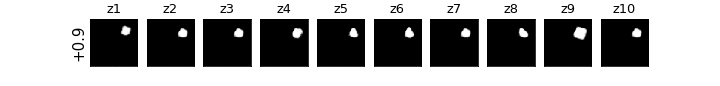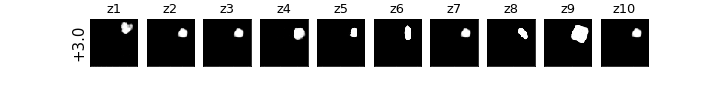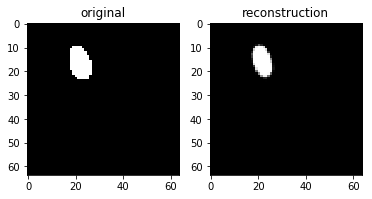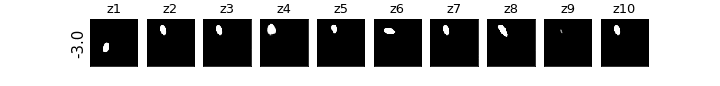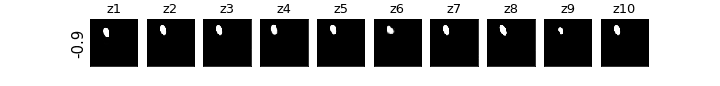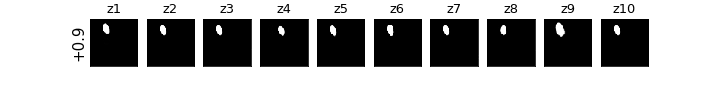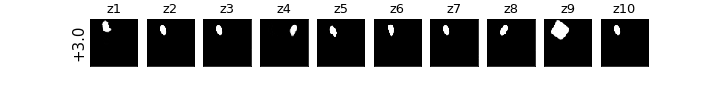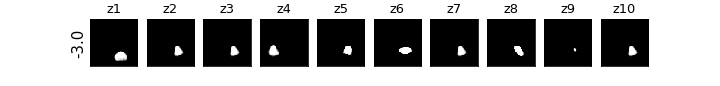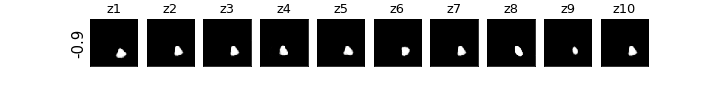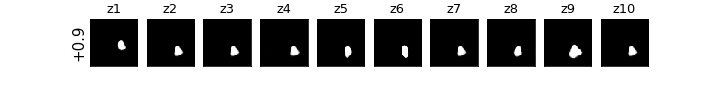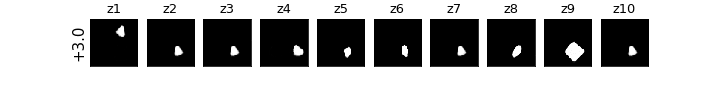Disentangling by Factorisingの概要
βVAEはdisentangleできるモデルだが,事前分布に近づける制約を大きくしているため,再構成がぼやけてしまう問題がある.
提案手法であるFactorVAEはTotal Correlation制約をいれることによって,再構成がぼやけてしまうことなしに,disentangleさせることを可能にした.
(詳しい説明は下スライド参照).

実装結果
各zの次元ごとに値を動かしたときの可視化
βVAE(CCI-VAE)
z1はy座標,z4はx座標,z8は回転,z9は大小がそれぞれ対応し,それぞれの要素のみが変化している(disentangleされている)ということがわかる.
チューニングをもっと頑張れば再構成ももっとキレイに生成できたと思われる.
FactorVAE
In progressです.実験結果がうまくいったら載せます.
pixyzを使った実装紹介
pixyzとは深層生成モデルを簡単に書くことができるライブラリである.
準備として,BetaVAEも簡単に実装した.
可視化も含めたすべての実装はここにあげた.
簡単に実装できる上,コードも非常に少なくてすむのでpixyzは素晴らしい.
pixyz参考
βVAE
Network Architecture
モデルはVAEと全く同じである.
Encoder(正規分布)とDecoder(ベルヌーイ分布)を用意する.
from pixyz.distributions import Normal, Bernoulli, Deterministic
import torch
import torch.nn as nn
from torch.nn import functional as F
class Encoder(Normal):
def __init__(self, z_dim=10):
super(Encoder, self).__init__(cond_var=["x"], var=["z"])
self.z_dim = z_dim
# encode
self.conv_e = nn.Sequential(
nn.Conv2d(1, 32, kernel_size=4, stride=2, padding=1), # 64 ⇒ 32
nn.BatchNorm2d(32),
nn.LeakyReLU(0.2),
nn.Conv2d(32, 64, kernel_size=4, stride=2, padding=1), # 32 ⇒ 16
nn.BatchNorm2d(64),
nn.LeakyReLU(0.2),
nn.Conv2d(64, 128, kernel_size=4, stride=2, padding=1), # 16 ⇒ 8
nn.BatchNorm2d(128),
nn.LeakyReLU(0.2),
)
self.fc_e = nn.Sequential(
nn.Linear(128 * 8 * 8, 1024),
nn.BatchNorm1d(1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, 2*self.z_dim),
)
def forward(self, x):
x = self.conv_e(x)
x = x.view(-1, 128 * 8 * 8)
x = self.fc_e(x)
mu = x[:, :self.z_dim]
scale = F.softplus(x[:, self.z_dim:])
return {"loc": mu, "scale": scale}
class Decoder(Bernoulli):
def __init__(self, z_dim=10):
super(Decoder, self).__init__(cond_var=["z"], var=["x"])
self.z_dim = z_dim
# decode
self.fc_d = nn.Sequential(
nn.Linear(self.z_dim, 1024),
nn.BatchNorm1d(1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, 128 * 8 * 8),
nn.LeakyReLU(0.2)
)
self.conv_d = nn.Sequential(
nn.ConvTranspose2d(128, 64, kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(64),
nn.LeakyReLU(0.2),
nn.ConvTranspose2d(64, 32, kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(32),
nn.LeakyReLU(0.2),
nn.ConvTranspose2d(32, 1, kernel_size=4, stride=2, padding=1),
nn.Sigmoid()
)
def forward(self, z):
h = self.fc_d(z)
h = h.view(-1, 128, 8, 8)
return {"probs": self.conv_d(h)}
Distribution
必要な確率分布を準備する.
上で作ったモデルをインスタンス化する.
z_dim=10
beta = 50
# prior model p(z)
loc = torch.tensor(0.).to(device)
scale = torch.tensor(1.).to(device)
prior = Normal(loc=loc, scale=scale, var=["z"], dim=z_dim, name="p_prior")
E = Encoder(z_dim=z_dim).to(device) # q(z|x)
D = Decoder(z_dim=z_dim).to(device) # p(x|z)
Loss
VAEと異なるのはLossの部分だけ.
βVAEの目的関数は,再構成誤差+β×制約項となる.
β=1のとき,VAEと全く同じ目的関数になることがわかる.
$$
E_{q_\phi(z|x)}\left[\log p_\theta(x|z)\right] - \beta KL(q_\phi(z|x)||p(z))
$$
from pixyz.losses import KullbackLeibler, CrossEntropy
reconst = CrossEntropy(E, D)
kl = KullbackLeibler(E, prior)
loss_cls = reconst.mean() + beta*kl.mean()
print(loss_cls)
# mean(-E_p(z|x)[log p(x|z)]) + mean(KL[p(z|x)||p_prior(z)]) * 50
model
あとはモデルに入れて訓練するだけ.非常にコードが短い.
model = Model(loss_cls, distributions=[E, D], optimizer=optim.Adam, optimizer_params={"lr":5e-4})
for i in range(5):
for batch_idx, x in tqdm(enumerate(train_loader)):
x = x.to(device)
loss = model.train({"x": x})
実は,単純なβVAEだとdisentangleさせるのが難しく,実験がうまくいかなかった.
βをめちゃくちゃ大きくすると,ある程度disentangleするようになったが,めちゃくちゃぼやけてしまった.
そのため,βVAEの改良版であるCCI-VAEを実装することにする.
CCI-VAE
βVAEのロスを工夫することで,disentangleさせることができる.
参考: Understanding disentangling in β-VAE
Loss
βを大きくしすぎると,zがxの情報をどんどん落としてしまうという問題があった.
そのため,β(ここではγ)を大きくしておく代わりに,Cをだんだん大きくしていくことによって,情報ボトルネックを解消したいという気持ちがある.
$$
E_{q_\phi(z|x)}\left[\log p_\theta(x|z)\right] - \gamma | KL(q_\phi(z|x)||p(z)) - C |
$$
Cは訓練中に変えていくので,変数として用意する.
論文にはγの値は1000にすると書いてあったが,あまりうまくいかなかったので80にした.
reconst = CrossEntropy(E, D)
kl = KullbackLeibler(E, prior)
C = Parameter("C")
loss_cls = reconst.mean() + gamma*(kl.mean()-C).abs()
Model
Cは0から25にかけて線形にepochに比例して大きくしていくようにする.
model = Model(loss_cls, distributions=[E, D], optimizer=optim.Adam, optimizer_params={"lr":5e-4})
N = len(train_loader)
for epoch in range(epoch_num):
for batch_idx, x in tqdm(enumerate(train_loader)):
x = x.to(device)
C_ = 25*(batch_idx+epoch*N)/(epoch_num*N)
loss = model.train({"x": x, "C": C_})
最終的にこちらの結果を上にのせている.
FactorVAE
Network Architecture
FactorVAEでは,βVAEのEncoderとDecoderに加え,Discriminatorも用意する.
このDiscriminatorはzの各次元を独立にさせるために必要.
class Discriminator(Deterministic):
def __init__(self, z_dim=10):
super(Discriminator, self).__init__(cond_var=["z"], var=["t"], name="d")
self.z_dim = z_dim
self.model = nn.Sequential(
nn.Linear(z_dim, 512),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(512, 256),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(256, 1),
nn.Sigmoid()
)
def forward(self, z):
t = self.model(z)
return {"t": t}
Distribution
確率分布を準備する.
ここで,InferenceShuffleDimは,zの各次元ごとにデータをばらばらにして出力するクラスである.
z_dim = 10
gamma = 10
# prior model p(z)
loc = torch.tensor(0.).to(device)
scale = torch.tensor(1.).to(device)
prior = Normal(loc=loc, scale=scale, var=["z"], dim=z_dim, name="p_prior")
E = Encoder(z_dim=z_dim).to(device) # q(z|x)
G = Decoder(z_dim=z_dim).to(device) # p(x|z)
D = Discriminator(z_dim=z_dim).to(device) # d(t|z)
class InferenceShuffleDim(Deterministic):
def __init__(self):
super(InferenceShuffleDim, self).__init__(cond_var=["x_"], var=["z"], name="q_shuffle")
def permute_dims(self, z):
B, _ = z.size()
perm_z = []
for z_j in z.split(1, 1):
perm = torch.randperm(B).to(z.device)
perm_z_j = z_j[perm]
perm_z.append(perm_z_j)
return torch.cat(perm_z, 1)
def forward(self, x_):
z = E.sample({"x": x_}, return_all=False)["z"]
return {"z": self.permute_dims(z)}
E_shuffle = InferenceShuffleDim()
Loss
FactorVAEの目的関数は,VAEの目的関数+Total Correlation(TC)である.
TCは,zのそれぞれの次元を独立にさせようという気持ちがある.
$$
E_{q_\phi(z|x)}\left[\log p_\theta(x|z)\right] - KL(q_\phi(z|x)||p(z)) - \gamma KL(q(z)||{\bar q}(z)) \
q(z) = \int p_{data}(x)q(z|x)dx \
{\bar q}(z) := \Pi_{j=1}^d q(z_j)
$$
reconst = CrossEntropy(E, G)
kl = KullbackLeibler(E, prior)
tc = AdversarialKullbackLeibler(E, E_shuffle, discriminator=D, optimizer=optim.Adam, optimizer_params={"lr":5e-4})
loss_cls = reconst.mean() + kl.mean() + gamma*tc
print(loss_cls)
# mean(-E_p(z|x)[log p(x|z)]) + mean(KL[p(z|x)||p_prior(z)]) + mean(AdversarialKL[p(z|x)||q_shuffle(z|x_)]) * 10
Model
discriminatorも学習させる必要があるので,いつものモデルの学習に加え,tc.train()も行っている.
model = Model(loss_cls, distributions=[E, G], optimizer=optim.Adam, optimizer_params={"lr":5e-4})
for i in range(10):
for batch_idx, x in tqdm(enumerate(train_loader)):
x = x.to(device)
loss = model.train({"x": x, "x_": x})
loss_d = tc.train({"x": x, "x_": x})
なぜか実験結果はうまくいっていないので調整中です.