pixyzとは
pixyzは深層生成モデルを簡単に書くことができるモデルです
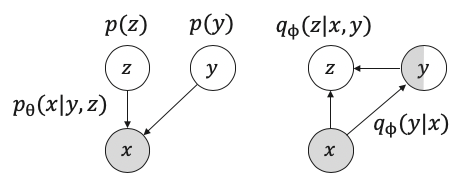
上の公式の図をみるとわかるように4つのブロックからなります.
下のブロックから積み重ねていくようにコードを書いていくと良いかと思われます.
今回は,下の論文を例にpixyzを使う練習もかねて実装してみました.
可視化も含めた全てのコードはここにあげました.
詳しくはpixyz公式を参照してください.
Semi-Supervised Learning with Deep Generative Models
元論文はこちら
一言で言えばVAEを半教師で学習できるモデルに拡張した論文です.
タスクはMNISTのラベルあり画像100枚とラベルなし画像59900枚を使って,10000枚のテスト画像のラベル予測精度をどれだけあげられるかということです.
M1モデル
M1モデルはVAEのことです.
M1モデルを使ってラベルを予測することを考えます.
Network Architecture
まず,ネットワーク構造を適当に書きます.models.pyとかによく入ってるやつです.
このとき普段のモデルの書き方と異なる点が3つほどあり,
- 確率分布を指定する. ex) class Encoder_m1(Normal)
- 変数を指定する. ex) cond_var=["x"], var=["z"]
- 分布に合わせたoutputを用意する. ex) {"loc": mu, "scale": scale}
ということです
from pixyz.distributions import Normal, Bernoulli, RelaxedCategorical
# q(z|x)
class Encoder_m1(Normal):
def __init__(self, z_dim=63):
super(Encoder_m1, self).__init__(cond_var=["x"], var=["z"], name="q")
self.z_dim = z_dim
self.conv_e = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=4, stride=2, padding=1), # 28 ⇒ 14
nn.BatchNorm2d(64),
nn.LeakyReLU(0.2),
nn.Conv2d(64, 128, kernel_size=4, stride=2, padding=1), # 14 ⇒ 7
nn.BatchNorm2d(128),
nn.LeakyReLU(0.2),
)
self.fc = nn.Sequential(
nn.Linear(128 * 7 * 7, 1024),
nn.BatchNorm1d(1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, 2*self.z_dim),
)
def forward(self, x):
x = self.conv_e(x)
x = x.view(-1, 128 * 7 * 7)
x = self.fc(x)
mu = x[:, :self.z_dim]
scale = F.softplus(x[:, self.z_dim:])
return {"loc": mu, "scale": scale}
# p(x|z)
class Decoder_m1(Bernoulli):
def __init__(self, z_dim=63):
super(Decoder_m1, self).__init__(cond_var=["z"], var=["x"])
self.z_dim = z_dim
self.fc_d = nn.Sequential(
nn.Linear(self.z_dim, 1024),
nn.BatchNorm1d(1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, 128 * 7 * 7),
nn.LeakyReLU(0.2)
)
self.conv_d = nn.Sequential(
nn.ConvTranspose2d(128, 64, kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(64),
nn.LeakyReLU(0.2),
nn.ConvTranspose2d(64, 1, kernel_size=4, stride=2, padding=1),
nn.Sigmoid()
)
def forward(self, z):
h = self.fc_d(z)
h = h.view(-1, 128, 7, 7)
return {"probs": self.conv_d(h)}
# latent classifier q(y|z)
class LatentClassifier(RelaxedCategorical):
def __init__(self, z_dim=63, y_dim=10):
super(LatentClassifier, self).__init__(cond_var=["z"], var=["y"], temperature=0.5, name="q")
self.fc = nn.Sequential(
nn.Linear(z_dim, 256),
nn.Dropout(p=0.4),
nn.ReLU(),
nn.Linear(256, y_dim),
nn.Dropout(p=0.4),
nn.Softmax(dim=1)
)
initialize_weights(self)
def forward(self, z):
out = self.fc(z)
return {"probs": out}
Distribution
VAEの潜在変数を使ってyを予測するモデルを考えます
z_dim = 63
# prior model p(z)
loc = torch.tensor(0.).to(device)
scale = torch.tensor(1.).to(device)
prior = Normal(loc=loc, scale=scale, var=["z"], dim=z_dim, name="p")
# initialize network
E = Encoder_m1().to(device) # q(z|x)
D = Decoder_m1().to(device) # p(x|z)
C = LatentClassifier().to(device) # q(y|z)
Loss
下限+対数尤度を最大化します.
すなわち,ロス = マイナス下限 + NLL となります.
$$
ELBO = E_{q_\phi(z|x)}\left[\log\frac{p_\theta(x, z)}{q_\phi(z|x)}\right] \
NLL = - E_{q_\phi(z|x)}[\log q_w(y|z)]
$$
同時分布p(x, z)が必要なので,定義します.
p(x|z)p(z)をかけるだけでなんとokです.
D_j = D * prior # P(x, z) = p(x|z)p(z)
D_j.to(device)
ロスのクラスにELBOとNLLがあります.
ロスをprintすると,定義したロスが出力されます.
from pixyz.losses import ELBO, NLL
elbo = ELBO(D_j, E)
nll = NLL(C)
# nllの係数
rate = 1 * (len(unlabel_loader) + len(label_loader)) / len(label_loader)
loss_cls = -elbo.mean() + (rate * nll).mean()
print(loss_cls) # -(mean(E_q(z|x)[log p(x,z)/q(z|x)])) + mean(log q(y|z) * 601.0)
Model
ここでは,最初に定義した分布をdistributionsのリストにいれ,optimizerを決め,与えられたデータを与えて訓練します.
from pixyz.models import Model
# 最適化
model = Model(loss_cls,test_loss=nll.mean(),
distributions=[E, D, C], optimizer=optim.Adam, optimizer_params={"lr":5e-4})
print(model)
モデルをprintすると,定義した分布や,ロスが出力されるので,間違いがないか確認できます.
Distributions (for training):
q(z|x), p(x|z), q(y|z)
Loss function:
-(mean(E_q(z|x)[log p(x,z)/q(z|x)])) + mean(log q(y|z) * 601.0)
Optimizer:
Adam (
Parameter Group 0
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
lr: 0.0005
weight_decay: 0
)
ELBOの入力はx_u, NLLの入力はzとyなので,modelに与えて訓練します.
zに関しては,E.sample({"x": x})とすることで,xで条件づけたときのzをサンプリングしています.
for epoch in range(100):
train_loss = 0
for (x, y), (x_u, y_u) in tqdm(zip(cycle(label_loader), unlabel_loader), total=len(unlabel_loader)):
x = x[:, 0:1].to(device)
y = torch.eye(10)[y].to(device)
x_u = x_u.to(device)
z = E.sample({"x": x})["z"]
loss = model.train({"y": y, "x": x_u, "z": z})
train_loss += loss
テスト画像のラベルの精度の推移
標準正規分布からのサンプリング結果
訓練できているようですが,思ったより汚い数字がでてきてしまいました.

M2モデル
M1モデルと同様に下から順に実装するだけです.
Network Architecture
# q(z|x, y)
class Encoder(Normal):
def __init__(self, z_dim=63, y_dim=10):
super(Encoder, self).__init__(cond_var=["x", "y"], var=["z"], name="q")
self.z_dim = z_dim
# encode
self.conv_e = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=4, stride=2, padding=1), # 28 ⇒ 14
nn.BatchNorm2d(64),
nn.LeakyReLU(0.2),
nn.Conv2d(64, 128, kernel_size=4, stride=2, padding=1), # 14 ⇒ 7
nn.BatchNorm2d(128),
nn.LeakyReLU(0.2),
)
self.fc1 = nn.Sequential(
nn.Linear(128 * 7 *7, 40),
)
self.fc2 = nn.Sequential(
nn.Linear(128 * 7 * 7, y_dim),
)
self.fc = nn.Sequential(
nn.Linear(40+y_dim, 1024),
nn.BatchNorm1d(1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, 2*self.z_dim),
)
def forward(self, x, y):
x = self.conv_e(x)
x = x.view(-1, 128 * 7 * 7)
x1 = self.fc1(x)
x2 = self.fc2(x)
x = torch.cat([x1, x2*y], dim=1)
x = self.fc(x)
mu = x[:, :self.z_dim]
scale = F.softplus(x[:, self.z_dim:])
return {"loc": mu, "scale": scale}
# p(x|z, y)
class Decoder(Bernoulli):
def __init__(self, z_dim=63, y_dim=10):
super(Decoder, self).__init__(cond_var=["z", "y"], var=["x"])
self.z_dim = z_dim
# decode
self.fc1 = nn.Sequential(
nn.Linear(self.z_dim, 40),
)
self.fc2 = nn.Sequential(
nn.Linear(self.z_dim, y_dim),
)
self.fc_d = nn.Sequential(
nn.Linear(40+y_dim, 1024),
nn.BatchNorm1d(1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, 128 * 7 * 7),
nn.LeakyReLU(0.2)
)
self.conv_d = nn.Sequential(
nn.ConvTranspose2d(128, 64, kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(64),
nn.LeakyReLU(0.2),
nn.ConvTranspose2d(64, 1, kernel_size=4, stride=2, padding=1),
nn.Sigmoid()
)
def forward(self, z, y):
z1 = self.fc1(z)
z2 = self.fc2(z)
z = torch.cat([z1, z2*y], dim=1)
h = self.fc_d(z)
h = h.view(-1, 128, 7, 7)
return {"probs": self.conv_d(h)}
# classifier q(y|x)
class Classifier(RelaxedCategorical):
def __init__(self, y_dim=10):
super(Classifier, self).__init__(cond_var=["x"], var=["y"], temperature=0.5, name="q")
self.input_height = 28
self.input_width = 28
self.conv1 = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=4, padding=2), # 28x28 ⇒ 14x14
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(2))
self.conv2 = nn.Sequential(
nn.Conv2d(64, 128, kernel_size=4, padding=2), # 14x14 ⇒ 7x7
nn.BatchNorm2d(128),
nn.ReLU(),
nn.MaxPool2d(2))
self.fc = nn.Sequential(
nn.Linear((self.input_height // 4) * (self.input_width // 4) * 128, 256),
nn.Dropout(p=0.4),
nn.ReLU(),
nn.Linear(256, y_dim),
nn.Dropout(p=0.4),
nn.Softmax(dim=1)
)
initialize_weights(self)
def forward(self, x):
c1 = self.conv1(x)
c2 = self.conv2(c1)
c2_flat = c2.view(c2.size(0), -1)
out = self.fc(c2_flat)
return {"probs": out}
Distribution
ラベルがあれば,そのままzを推論し,ラベルがなければxからyを推論したあと,zを推論するモデル
z_dim = 63
# prior model p(z)
loc = torch.tensor(0.).to(device)
scale = torch.tensor(1.).to(device)
prior = Normal(loc=loc, scale=scale, var=["z"], dim=z_dim)
# initialize network
E = Encoder().to(device) # q(z|x, y)
D = Decoder().to(device) # p(x|z, y)
C = Classifier().to(device) # q(y|x)
D_j = D * prior # p(x, z| y) = p(x|z, y)p(z)
D_j.to(device)
今回は,同じモデルにラベルデータ及びアンラベルデータを入力するため,変数を置き換えたものを新しく定義します.
(モデルのパラメタは共有されます)
# distributions for unsupervised learning
Eu = E.replace_var(x="x_u", y="y_u") # q(z|x_u, y_u)
Du = D.replace_var(x="x_u", y="y_u") # p(x_u|z, y_u)
Cu = C.replace_var(x="x_u", y="y_u") # q(y_u|x_u)
ECu = Eu * Cu # q(z, y_u|x_u) = q(z|x_u, y_u)q(y_u|x_u)
Du_j = Du * prior # p(x_u, z| y_u) = p(x_u|z, y_u)p(z)
Du_j.to(device)
ECu.to(device)
Cu.to(device)
Loss
M1のときと同様に愚直にロスを書きます
$$
Elbo = E_{q_\phi(z|x, y)}\left[\log\frac{p_\theta(x, z|y)}{q_\phi(z|x, y)}\right] \
ElboU = E_{q_\phi(z, y|x)}\left[\log\frac{p_\theta(x, z|y)}{q_\phi(z, y|x)}\right] \
NLL = - E_{q_\phi(z|x)}[\log q_w(y|z)]
$$
elbo = ELBO(D_j, E)
elbo_u = ELBO(Du_j, ECu)
nll = NLL(C)
rate = 1 * (len(unlabel_loader) + len(label_loader)) / len(label_loader)
loss_cls = -elbo_u.mean() -elbo.mean() + (rate * nll).mean()
print(loss_cls)
# -(mean(E_p(z,y_u|x_u)[log p(x_u,z|y_u)/p(z,y_u|x_u)])) - mean(E_q(z|x,y)[log p(x,z|y)/q(z|x,y)]) + mean(log p(y|x) * 601.0)
Model
M1と同様
model = Model(loss_cls,test_loss=nll.mean(),
distributions=[E, D, C], optimizer=optim.Adam, optimizer_params={"lr":5e-4})
print(model)
Distributions (for training):
q(z|x,y), p(x|z,y), p(y|x)
Loss function:
-(mean(E_p(z,y_u|x_u)[log p(x_u,z|y_u)/p(z,y_u|x_u)])) - mean(E_q(z|x,y)[log p(x,z|y)/q(z|x,y)]) + mean(log p(y|x) * 601.0)
Optimizer:
Adam (
Parameter Group 0
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
lr: 0.0005
weight_decay: 0
)
for epoch in range(100):
train_loss = 0
for (x, y), (x_u, y_u) in tqdm(zip(cycle(label_loader), unlabel_loader), total=len(unlabel_loader)):
x = x[:, 0:1].to(device)
y = torch.eye(10)[y].to(device)
x_u = x_u.to(device)
loss = model.train({"x": x, "y": y, "x_u": x_u})
train_loss += loss
テスト画像のラベルの精度の推移
100ラベルで学習したにもかかわらず,最終的に精度が0.91くらいでています.
論文に報告されている通りなので,正しい実装ではないかと思われます.

標準正規分布+ラベルを固定したときのサンプリング結果
ラベルとスタイルのdisentangleもされている上,数字もきれいにサンプリングされたことがわかります.
M1+M2モデル
M1とM2を組み合わせることで,半教師ありの精度が96%を超えるということが報告されています.
実装としては,元論文と同様にM1を学習し,その後M2を学習する,end-to-endではない方法で実験を行います.
M1を100epoch学習させたあと,M2を200epoch学習させました.
Loss
$$
ElboM1 = E_{q_\phi(z_1|x)}\left[\log\frac{p_\theta(x, z_1)}{q_\phi(z_1|x)}\right] \
ElboM2 = E_{q_\phi(z_2|z_1, y)}\left[\log\frac{p_\theta(z_2, z_1|y)}{q_\phi(z_2|z_1, y)}\right] \
ElboM2U = E_{q_\phi(z_2, y|z_1)}\left[\log\frac{p_\theta(z_2, z_1|y)}{q_\phi(z_2, y|z_1)}\right] \
NLL = - E_{q_\phi(z_1|x)}[\log q_w(y|z_1)]
$$
テスト画像のラベルの精度の推移
チューニングが難しく,0.80止まりの精度となってしまいました,

標準正規分布+ラベルを固定したときのサンプリング結果
数字は最初からきれいにサンプリングされていますが,スタイルとラベルのdisentangleはあまりされていないようにみえます.
その他
感想
サンプリングとか,対数尤度とかが確率分布からサクッと計算できるのでハマりそう.
何気に正規分布や離散分布のリパラメタリゼーションすら内包されているのでなにも考えなくてよいところも良いです.
参考
公式のM2.ipynb