0. 注記
WindowsAPIのソースコードは調べられなかったので、実験ベースでの検証になります。
コード例はC#です。
「コードはよ」というかたは、最後の章へ。
マルチモニタでの挙動は未検証です。
1. 絶対座標指定でのSendInputを使ったマウスカーソルの移動
現在のマウスカーソル位置とは関係なくデスクトップ上の指定の座標にマウスカーソルを移動させたいとき、MOUSEEVENTF_ABSOLUTEを指定してSendInput(Windows API)を使ってマウスを制御します。
※移動させるだけなら Cursor.Position に座標を設定してもやれるようです。マウスボタン操作を合わせてやりたい場合はSendInputを使うことになるかと思います。
巷(ちまた)には下記のような変換をしているコードがあふれていますが、これらを使うと、丸め誤差により、もともとの意図した座標(x, y)からずれます。
(例2や例3は、ズレは1ピクセルとかになると思うので通常は気にならないレベルですが、シーンによっては問題になり得ます。)
absX = x * (65535 / Screen.PrimaryScreen.Bounds.Width);
absY = y * (65535 / Screen.PrimaryScreen.Bounds.Height);
NG例1については、C言語やC#等は/が整数除算になるので、係数(65535 / Screen.PrimaryScreen.Bounds.Width) を計算した時点で、モニタのWidth,Heightに依存した誤差をもってしまいます。1
勘の良い方なら、NG例2を使うでしょう。
absX = (x * 65535) / Screen.PrimaryScreen.Bounds.Width;
absY = (y * 65535) / Screen.PrimaryScreen.Bounds.Height;
もしくは、分子が(65536から)1引いているのだから、分母も同じく1を引いて、下記を使う方もいると思います。
absX = (x * 65535) / (Screen.PrimaryScreen.Bounds.Width - 1);
absY = (y * 65535) / (Screen.PrimaryScreen.Bounds.Height - 1);
2. 公式サイトのSendInputの仕様記載がそもそもイケてない
NG例2やNG例3をみて、「いやいや、Microsoftの公式サイトに書いてあるし、あってるでしょ?」と思う方もおられるかと思います。(自分もそう思ってました。)
公式サイトの記載を抜粋します。
If MOUSEEVENTF_ABSOLUTE value is specified,
dx and dy contain normalized absolute coordinates between 0 and 65,535.
The event procedure maps these coordinates onto the display surface.
Coordinate (0,0) maps onto the upper-left corner of the display surface;
coordinate (65535,65535) maps onto the lower-right corner.
In a multimonitor system, the coordinates map to the primary monitor.
これを見ると、あたかも(65535,65535)とプライマリモニタの(Width,Height)もしくは(Width-1,Height-1)が対応しているように見えます。
ですが、実際にNG例2やNG例3のコードでやってみるとずれます。
ずれるケースの実験は本記事では省略しますが、この記事のコードを使えば確認できます。
3. 指定した座標 と 実際の移動後の座標 の関係を調べてみた
3章では、指定した座標に対しSendInput実行後のマウスカーソル座標がどこになるのかを調べます。
この章で、SendInputの世界の座標系(0,0)-(65535(?),65535(?)) から ピクセル単位の座標系を取得する式を得ます。
最終的に得たいのは、これと逆方向の変換です。それについては4章で扱います。
3.1. 結論
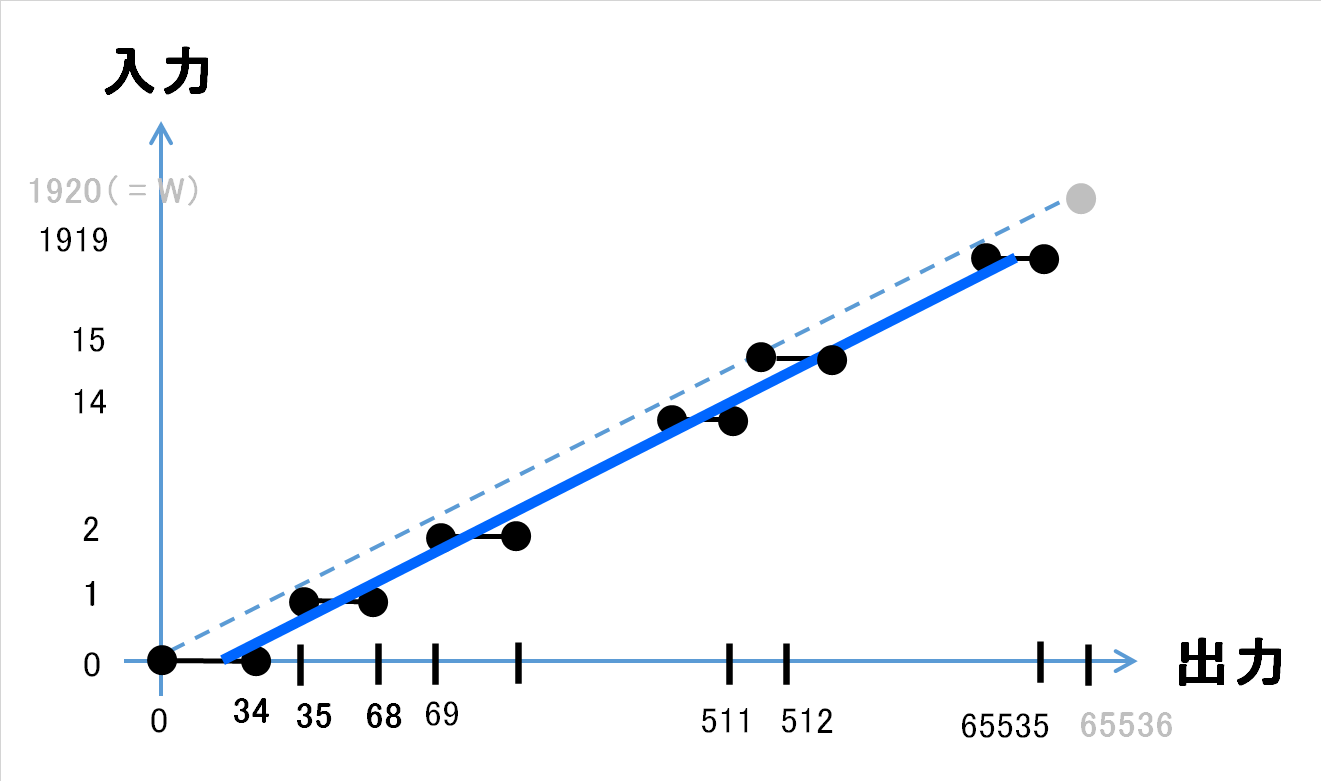
実験により検証したところ、(0,0)-(65536,65536)とプライマリモニタの(0,0)-(Width,Height)が対応関係にあります。丸め方向は切り捨てです。
つまり、SendInput APIは、内部で Cursor.Position.X = (absX * Width) / 65536; に相当する計算(整数除算)をしているようです。
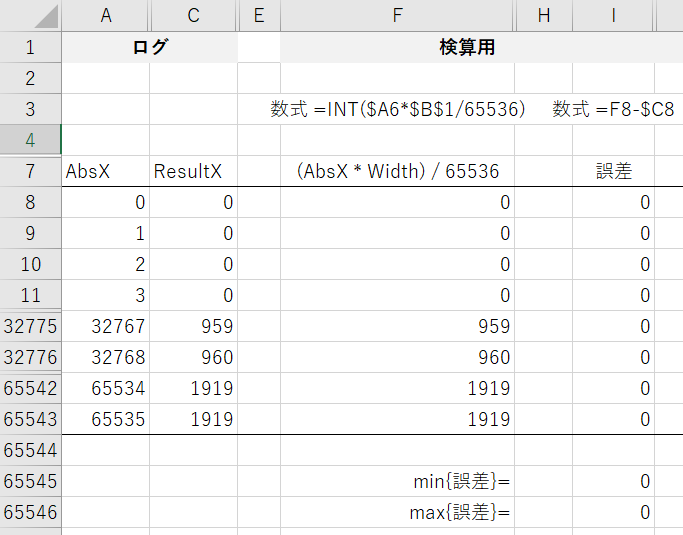
3.2. それっぽいエビデンス
AbsXが、SendInputに指定した x の値。
ResultXが、.NetのCursor.Positionプロパティで取得した実際のマウスカーソル座標です。
(行挿入等の操作をしてしまったので数式のセル参照がメモとずれてます)
3.3. 実験に使用したソースコード
高解像度による座標系変換の影響を受けると問題がややこしくなるので、SetProcessDPIAware (Windows API)で高解像度対応させています。
using System;
using System.Drawing;
using System.IO;
using System.Runtime.InteropServices;
using System.Threading;
using System.Threading.Tasks;
using System.Windows.Forms;
class MainForm : Form
{
readonly int sweepStep = 1; // SendInputに送信するx座標ベース
bool abortFlag;
// SendInputに送信する終端x,y座標。コマンドライン引数経由で設定。
// (memo: コマンドライン引数はintで受けておき、sweep中のfor文でのoverflow防止のためlongでもっている。)
long _lastAbsX;
long _lastAbsY;
string _directionOption; // "d": ななめ(Diagonal)(x,yを同時にsweep) それ以外: 水平と垂直
MainForm(int lastAbsX, int lastAbsY, string directionOption)
{
abortFlag = false;
_directionOption = directionOption;
_lastAbsX = lastAbsX;
_lastAbsY = lastAbsY;
ClientSize = new System.Drawing.Size(300,100);
Load += (s,e)=>{SendMouseMove();};
FormClosing += (s,e)=>{abortFlag=true;};
}
private static class NativeMethods
{
[DllImport("user32.dll", SetLastError = true)]
public extern static void SendInput(int nInputs, Input[] pInputs, int cbsize);
[DllImport("user32.dll", SetLastError = true)]
public extern static IntPtr GetMessageExtraInfo();
[DllImport( "user32.dll" )]
public static extern bool SetProcessDPIAware();
}
[StructLayout(LayoutKind.Sequential)]
private struct POINT
{
public int x;
public int y;
}
[StructLayout(LayoutKind.Sequential)]
struct MouseInput
{
public int X;
public int Y;
public int Data;
public int Flags;
public int Time;
public IntPtr ExtraInfo;
}
[StructLayout(LayoutKind.Sequential)]
struct KeyboardInput
{
public short VirtualKey;
public short ScanCode;
public int Flags;
public int Time;
public IntPtr ExtraInfo;
}
[StructLayout(LayoutKind.Sequential)]
struct HardwareInput
{
public int uMsg;
public short wParamL;
public short wParamH;
}
[StructLayout(LayoutKind.Sequential)]
struct Input
{
public int Type;
public InputUnion ui;
}
[StructLayout(LayoutKind.Explicit)]
struct InputUnion
{
[FieldOffset(0)]
public MouseInput Mouse;
[FieldOffset(0)]
public KeyboardInput Keyboard;
[FieldOffset(0)]
public HardwareInput Hardware;
}
private const int MOUSEEVENTF_MOVE = 0x0001;
private const int MOUSEEVENTF_ABSOLUTE = 0x8000;
void SendMouseMove()
{
BeginInvoke(
(MethodInvoker)delegate(){
checked{
var scrs = Screen.AllScreens;
for(int i=0;i<scrs.Length;i++) {
if(abortFlag){return;}
Console.Write("Size of screen[");
Console.Write(i);
Console.Write("]\t");
Console.Write(scrs[i].Bounds.Width);
Console.Write("\t");
Console.WriteLine(scrs[i].Bounds.Height);
Console.Write("Location of screen[");
Console.Write(i);
Console.Write("]\t");
Console.Write(scrs[i].Bounds.Left);
Console.Write("\t");
Console.WriteLine(scrs[i].Bounds.Top);
}
if ( _directionOption == "d" ) {
// 左上(0,0)から右下(_lastAbsX,_lastAbsY)まで斜めに移動させてx,yを同時に動かして座標を出力させる。
for ( long i = 0 ; i < _lastAbsX + sweepStep ; i += sweepStep ) {
if(abortFlag){return;}
long x = i;
if ( x > _lastAbsX ){x = _lastAbsX;}
long y = (x * _lastAbsY) / _lastAbsX;
SendInputMouseMoveAndDumpPoint((int)x, (int)y);
}
}
else {
// 左上(0,0)から(_lastAbsX,0)まで直線状に移動させてx,yを出力させる。
for ( long i = 0 ; i < _lastAbsX + sweepStep ; i += sweepStep ) {
if(abortFlag){return;}
long x = i;
if (x > _lastAbsX) {x = _lastAbsX;}
SendInputMouseMoveAndDumpPoint((int)x, 0);
}
// 左上(0,0)から(0,_lastAbsY)まで直線状に移動させてx,yを出力させる。
for ( long i = 0 ; i < _lastAbsY + sweepStep ; i += sweepStep ) {
if(abortFlag){return;}
long y = i;
if (y > _lastAbsY) {y = _lastAbsY;}
SendInputMouseMoveAndDumpPoint(0, (int)y);
}
}
}
MessageBox.Show("Completed.");
}
);
}
static void SendInputMouseMoveAndDumpPoint(int absX, int absY)
{
SendInputMouseMove(absX, absY);
DumpPoint(absX, absY);
}
static void DumpPoint(int orgAbsX, int orgAbsY)
{
Point p = Cursor.Position;
Console.Write(orgAbsX);
Console.Write("\t");
Console.Write(orgAbsY);
Console.Write("\t");
Console.Write(p.X);
Console.Write("\t");
Console.WriteLine(p.Y);
}
private static void SendInputMouseMove(int absX, int absY)
{
var mv = new Input();
mv.Type = 0; // MOUSE = 0
mv.ui.Mouse.X = absX;
mv.ui.Mouse.Y = absY;
mv.ui.Mouse.Data = 0;
mv.ui.Mouse.Flags = MOUSEEVENTF_ABSOLUTE | MOUSEEVENTF_MOVE;
mv.ui.Mouse.Time = 0;
mv.ui.Mouse.ExtraInfo = IntPtr.Zero;
Input[] inputs = new Input[]{mv};
NativeMethods.SendInput(inputs.Length, inputs, Marshal.SizeOf(inputs[0]));
}
[STAThread]
static void Main(string[] args)
{
NativeMethods.SetProcessDPIAware(); // 高解像度のスケーリング座標に対応するため
int lastAbsX;
int lastAbsY;
string directionOption;
if ( args.Length==0 ) {
lastAbsX = 65535;
lastAbsY = 65535;
directionOption = "d";
}
else if ( args.Length==3 ) {
try{
lastAbsX = Convert.ToInt32(args[0]);
lastAbsY = Convert.ToInt32(args[1]);
}
catch(FormatException){
return;
}
catch(OverflowException){
return;
}
if(lastAbsX<0){return;}
if(lastAbsY<0){return;}
directionOption = args[2];
}
else {
return;
}
Application.Run(new MainForm(lastAbsX,lastAbsY,directionOption));
}
}
4. じゃあどうすればよいの?
3章で得られた関係性 Cursor.Position.X = (absX * Width) / 65536;の
逆計算をすることでマウスカーソルの座標系から0~65536の座標系に変換する。
というアプローチで行きます。
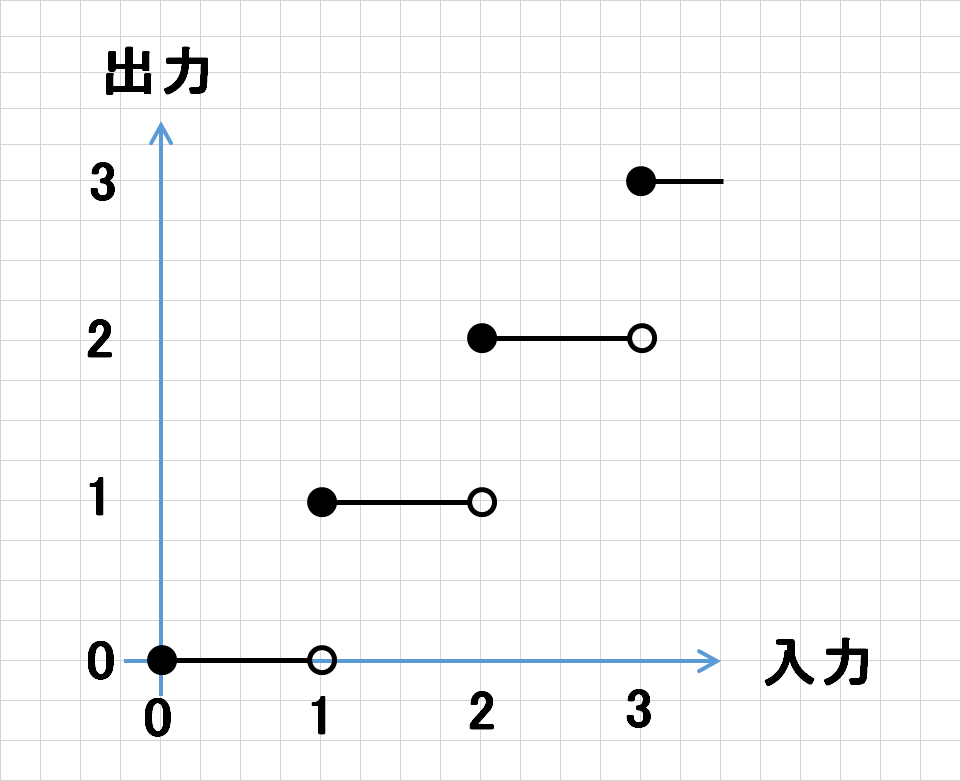
4.1. 床関数
整数除算の際の丸め処理2は、大雑把にいうと、小数点以下を切り捨てているのと同じなので、床関数と同じと考えることができます。
床関数のグラフの描くとこんな感じになります。(白抜きの〇は、含まない。)
4.2. 逆計算のイメージ
モニタのWidth, Heightが65536以下である仮定のもと、実際の例 Width = 1920 のときの逆計算のイメージをグラフで描くと下図のようになります。
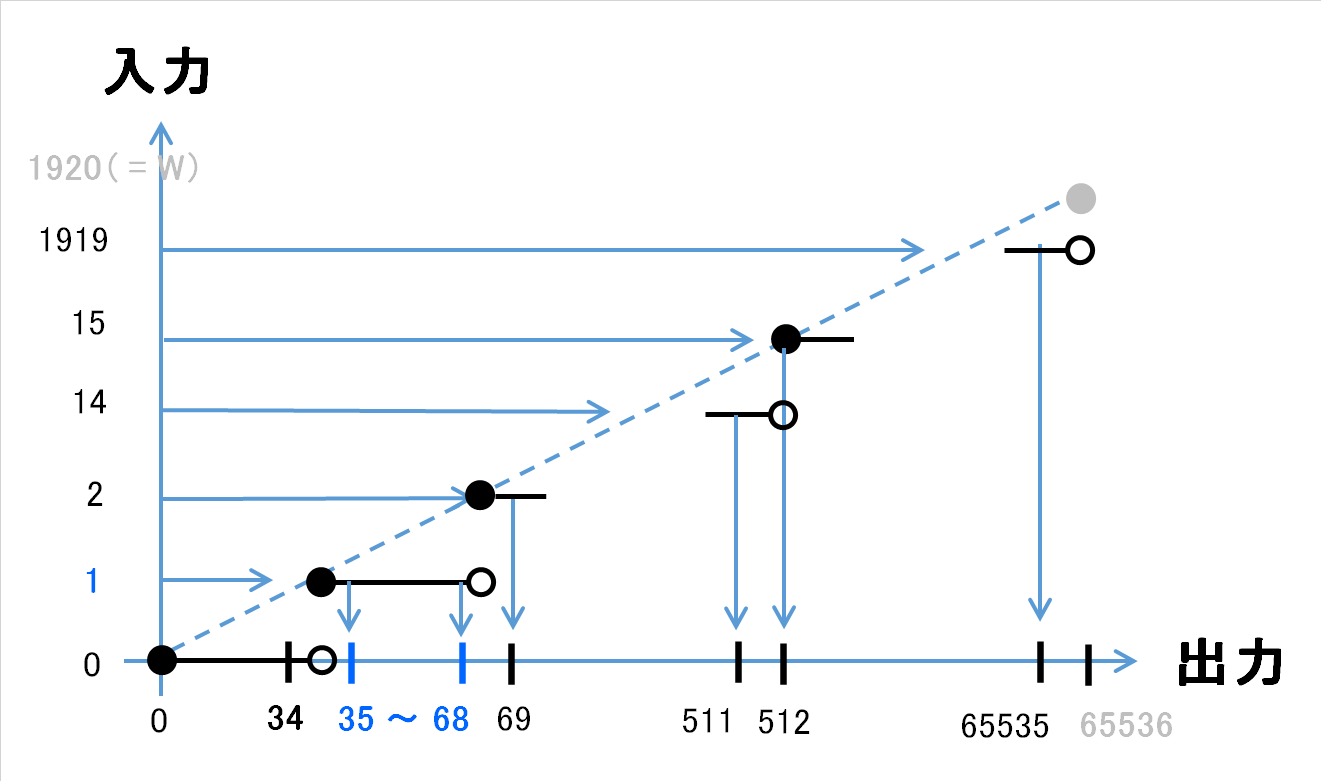
カーソル位置x=1に動かしたい場合は、35~68の範囲に収まる値をSendInputのabsXに設定してやる必要があります。3
なので、グラフ上の各線分●ー○よりも内側を貫く直線で逆計算の式を構築する必要があります。(語彙力・・・)
ちょっと雑ですが、下図のイメージです。
4.3. 逆計算の式
話がとびますが、直感に頼って式の案を出すと、天井関数を使って
absX = ceiling((Cursor.Position.X * 65536) ÷ Width)
として計算すればイケそう(4.2.章の内容を満たせそう)な気がします(超乱暴)。(ここでの÷は実数での除算を表しているとします。)
Excelで検算をしたところ、Width=1920, Height=1080の環境では誤差がでないようです。
イメージこんな感じ。
See the Pen Conversion graph of SendInput by kob58im (@kob58im) on CodePen.
4.4. 結論(正確に変換できるであろうコード)
4.3章の変換式をソースコード(C#)にすると、下記のようになります。
下記の「正確に変換できるであろうコード」は、最終的に4.3章にて直感で出しており、4.2章で言及した変換ができているかどうか数学的な証明もしていないので、参考扱いとしてください。
absX = (x * 65536 + Screen.PrimaryScreen.Bounds.Width -1) / Screen.PrimaryScreen.Bounds.Width;
absY = (y * 65536 + Screen.PrimaryScreen.Bounds.Height-1) / Screen.PrimaryScreen.Bounds.Height;
注: x または y が 30000くらいの大きな値をとりえるならば、long型にキャストすること。
4.5. 証明してみる
完全に自己満足の世界だが、証明しておかないと落ち着かないので、証明してみた。
65536の代わりに一般化して $ N $ と置きます。モニタの幅Widthを $ W $ と置きます。 $ N \geq W $ と仮定します。
p = \frac{N}{W}
と置きます。 $ x $ を カーソルのx座標とします。
このとき、4.3章で案として挙げた式は天井関数 $ \lceil x\rceil $ を使って下記と書けます。
f(x) = \lceil x \cdot p \rceil
また、SendInputの座標系からカーソルのx座標に変換する関数を $ g $ と書くと、床関数 $ \lfloor x\rfloor $ を使って下記で表せます。
g(y) = \biggl\lfloor y \cdot \frac{1}{p} \biggr\rfloor
以降で $ f(x) $ が、「4.2章最下部のグラフの各区間の左端の出力値を取ることを示します。
つまり
g(f(x) -1) = x-1 \cdots\cdots ①
が成立することを証明します。
上記を4.2章のグラフのイメージで描くと下記のようになります。
①の $ g $ を展開すると、
① \Leftrightarrow\biggl\lfloor (f(x) -1) \cdot \frac{1}{p} \biggr\rfloor = x-1
$ \lfloor y \rfloor = C $ なら $ C \leq y < C+1 $ なので、
① \Leftrightarrow x-1 \leq (f(x) -1) \cdot \frac{1}{p} < x
すべての辺に $ p $ を乗算し、さらに $ f(x) $ を展開すると、
① \Leftrightarrow (x-1)\cdot p \leq \lceil x \cdot p \rceil -1 < x \cdot p
$ x \cdot p $ を $ z $ と置き、すべての辺に $ 1 $ を加算すると、
① \Leftrightarrow z-(p-1) \leq \lceil z \rceil < z + 1
$ p - 1 \geq 0 $ なので、上記は常に成立する。以上で証明できた。
-
プライマリモニタのWidthが1920だとすると、係数は34.1328125が丸められて34になります。xが1919のとき、実数上の除算だとabsXは65,500.8671875ですが、係数は34に丸められておりabsXは65,246となります。その差は-254.8671875となり、65535に対して約0.4%の誤差であることが分かります。この0.4%(=0.004)とWidth-1(=1919)を乗算すると、7~8ピクセルほどのズレになります。 ↩
-
ここでは負の数はとりあえず考えないようにします。 ↩
-
公式のAPIの説明上の名称はabsXではなく
dxです。dxだと微分やDifferenceの略のイメージから「差分」を連想するので、記事中では絶対座標をイメージしやすいようにabsXとしています。 ↩