[Python]【補足】04章-09 いろいろなデータ構造（セットにおける集合理論と演算）

#[Python]【補足】04章-09 セットにおける集合理論と演算
この節では集合理論の話と演算について触れていきます。主に高校数学の範囲で扱う内容となり、少し理論的なお話が多くなると思います。

そのためこの節は【補足】としていますので飛ばしていただいても構いません。

ただし、基本情報技術者試験を受験しようとしている方や、午後問題でPythonの選択を考えている方は基礎理論分野で集合の話が出題されますので目を通しておきましょう。

##集合におけるベン図
まず、集合理論を説明するために、Python consoleに以下のコードを入力してセットを作成しましょう。

.py

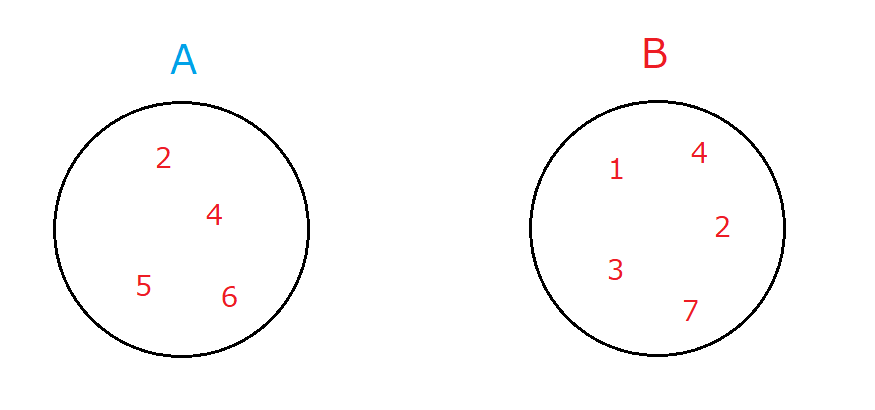
>>> A = {2, 4, 5, 6}
>>> B = {1, 2, 3, 4, 7}
>>> A
{2, 4, 5, 6}
>>> B
{1, 2, 3, 4, 7}

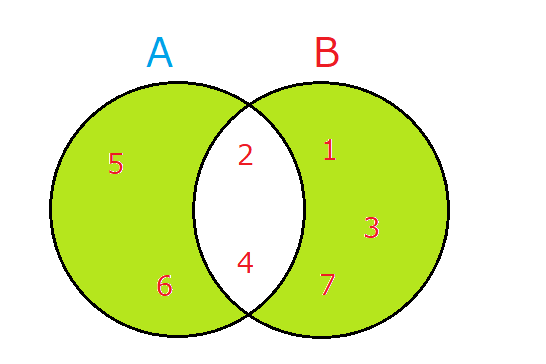
今回は2つのセットを作成しましたが、図で表記するとそれぞれ以下の通りになります。
この図のことをベン図と言います。

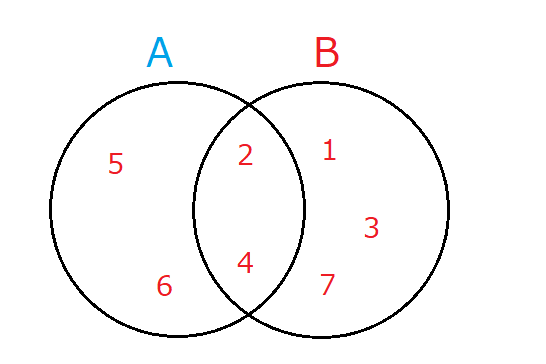
このベン図を見てわかる通り、それぞれAとBの中に**{2, 4}**がそれぞれのセットに共通して存在します。そのため、以下のようにベン図を表現することができます。

##集合における理論
ここでは理論的なお話が多いため、「セット」という表現でなく、「集合」という一般的な表現で説明していきます。

集合とは、ある条件で集まった集合体のことを言います。上記例では数値の集合を作成しましたが、例えば集合X「髪の毛の長さが１cm未満の人」、集合Y「身長が170cm以上の人」といったものが条件です。

これが例えば、「髪の毛の長さが短い人」「身長が高い人」というのは人の主観によって変わってくるので、これは条件とは言いません。
具体的には、数値で表現されたものが条件と考えてください。

##集合演算
ここでは、集合における演算を紹介していきます。

####和集合
2つの集合を加算したものです。先ほどの集合Aと集合Bの例でいえば、どちらか1つ以上の集合に含まれるものが出力されます。（OR演算ということがある。）
以下の表記のいずれかの方法で表します。

A∪B, 　A+B, 　A∨B, 　A　or　B

したがって、以下のように表現できます。

A∪B = \{1, 2, 3, 4, 5, 6, 7\}

ベン図で表すと以下の色を塗ったところが該当します。

Pythonで実装すると以下の通りになります。
（キーボードの「¥記号」のところにある**|**（バー）を用います。）

.py

>>> A | B
{1, 2, 3, 4, 5, 6, 7}

または、unionメソッドを用いても演算可能です。

.py

>>> A.union(B)
{1, 2, 3, 4, 5, 6, 7}

####積集合
2つの集合を乗算したものです。先ほどの集合Aと集合Bの例でいえば、両方の集合に含まれるものが出力されます。（AND演算ということがある。）
以下の表記のいずれかの方法で表します。

A∩B, 　A・B, 　A∧B, 　A　and　B

したがって、以下のように表現できます。

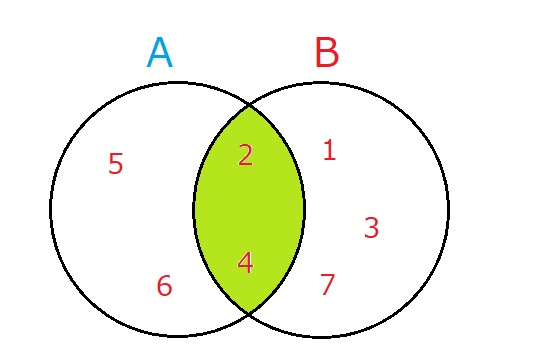
A∩B = \{2, 4\}

ベン図で表すと以下の色を塗ったところが該当します。

Pythonで実装すると以下の通りになります。

.py

>>> A & B
{2, 4}

または、intersectionメソッドを用いても演算可能です。

.py

>>> A.intersection(B)
{2, 4}

####差集合
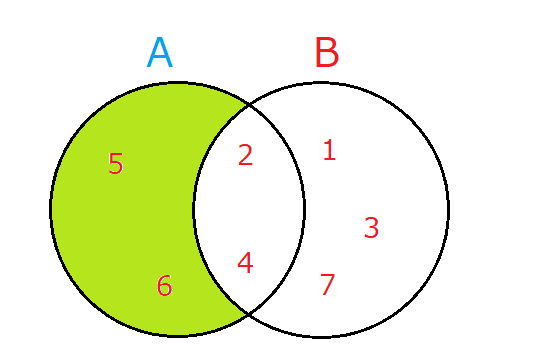
ある集合から、別の集合の要素を差し引いたものです。先ほどの集合Aと集合Bの例でいえば、集合Aには含まれるけど集合Bには含まれないものが出力されます。
以下の表記の方法で表します。

A-B

したがって、以下のように表現できます。

A-B = \{5, 6\}

ベン図で表すと以下の色を塗ったところが該当します。

Pythonで実装すると以下の通りになります。

.py

>>> A - B
{5, 6}

または、differenceメソッドを用いても演算可能です。

.py

>>> A.difference(B)
{5, 6}

####対象差集合
少し難しい表現となりますが、2つの集合のうち、どちらかの条件にあてはまるものから、両方の条件にあてはまるものを差し引いたものが出力されます（XOR演算ということがある。）
どういうことかと言いますと、差集合でA-BとB-Aを行って、それぞれをOR演算したものです。
以下の表記の方法で表します。

A⊕B, 　A　xor　B

したがって、以下のように表現できます。

A⊕B = \{1, 3, 5, 6, 7\}

ベン図で表すと以下の色を塗ったところが該当します。

Pythonで実装すると以下の通りになります。

.py

>>> A ^ B
{1, 3, 5, 6, 7}

または、symmetric_differenceメソッドを用いても演算可能です。

.py

>>> A.symmetric_difference(B)
{1, 3, 5, 6, 7}

####補集合
ある集合の否定を意味します。集合Aに含まれないという意味です。（NOT演算ということがある。）
なお、補集合についてはPythonでは実装は不可能となります。
以下の表記の方法で表します。

\overline{A},　not A

したがって、以下のように表現できます。

\overline{A} = {1, 3, 7}

ベン図で表すと以下の色を塗ったところが該当します。

※補集合は集合A以外の部分が範囲となります。したがって、集合Bについても範囲であるし、外の部分も範囲となります。

##部分集合
部分集合とは集合の中にさらに集合を含んだ状態です。ベン図で表現すると以下の通りです。ここでは集合Pと集合Qで表現します。

まずは、Python Consoleからセットを作成してみます。

.py

>>> P = {1, 2, 3, 4, 5, 6, 7}
>>> Q = {3, 5}
>>> P
{1, 2, 3, 4, 5, 6, 7}
>>> Q
{3, 5}

この状態で、積集合を表現すると、以下の通りになります。

.py

>>> P & Q
{3, 5}

集合Pと集合Qの重複部分が表示されています。これは先ほど説明した積集合の結果と同じことを確認できます。

では、集合Qが集合Pに含まれていることを表現するにはどうしたらよいでしょうか？
以下の表記の方法で表します。

Q⊂P,　Q⊆P

つまり、PにQが含まれている（包含されている）ということを表現します。

これをPythonで実装していきますが、Python上では包含されているかどうかを判定することができます。
以下のコードを入力してください。一度変数P, Q、そしてAの内容を表示してから実行します。

.py

>>> P
{1, 2, 3, 4, 5, 6, 7}
>>> Q
{3, 5}
>>> A
{2, 4, 5, 6}
>>> Q <= P
True
>>> Q <= A
False

Pythonで集合の包含関係の判定をするには**<=を用います。
Qの要素はPに含まれているのでTrueが出力されますが、Qの要素はAに含まれているものが一部存在しないのでFalse**と出力されます。

または、issubsetメソッドを用いても演算可能です。

.py

>>> Q.issubset(P)
True

##最後に
今回はいろいろな集合演算に触れました。集合演算は種類が多いですが、情報処理技術者試験ではよく出題されるものばかりです。ぜひ押さえておきましょう。

###【目次リンク】へ戻る