最近、A Visual Exploration of Gaussian Processesというサイトを見ました。今まであまりよく理解できていなかったカーネル法やガウシアンRBFカーネルを視覚的に見ることができて理解が深まった気がします(理解したとはいっていない)。
これを真似すれば、以前書いたWAEの記事でのIMQ関数も理解が深まるのではないかと思い、やってみました。
TL;DR
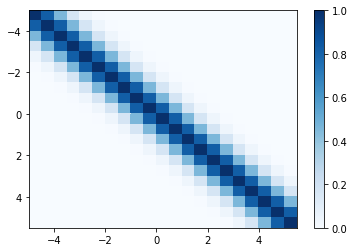
jupyter notebookで以下のような感じのグラフ可視化ができました。
コード全体はgithubに掲載してあります。
RBFについて
自分はこれまでRadial basis kernel(RBF)について誤解していたのですが、RBFにも種類が複数あり一般にSVMなどで単に「RBFカーネル」として紹介されるのはGaussian kernelであるようです。
定義
k(x, y) = \exp \left(- \frac{ ||x - y||^2}{2\sigma^2} \right)
他の書き方もあるようです。
k(x, y) = \exp \left(- \gamma ||x - y||^2 \right)
これは単に $\gamma = \frac{1}{2\sigma^2}$ と表現しているだけで同じものだと理解できました。
IMQについて
Inverse Multiquadric(IMQ)はRBFカーネルの一種で日本語では逆多重二乗RBFという名称がついているようです。
こちらも異なる式での解説が複数見受けられます。Wikipediaでの記述に習いつつ、表記を合わせると以下になるでしょう。
k(x, y) = \frac {1} {\sqrt{1 + \epsilon ||x - y||^2} }
先の自分の記事から貼ったリンク(PDF)でも同じ式が示されています。
一方で、César Souzaの解説記事ではちょっと違った式になっています。
k(x, y) = \frac{1}{\sqrt{||x - y||^2 + c^2 }}
$||x-y||$は頻出するので以下$r = ||x - y||$とします。分母の平方根の中身に着目すると、
r^2 + c^2 = 1 + \epsilon r^2 \\
c^2 = 1 + \epsilon r^2 - r^2 \\
c^2 = 1 + ( \epsilon -1) ||x - y||^2
と考えれば内容は同じだと考えられます。ただし$c^2 > 0$なのでこの場合$\epsilon \geq 1$となるような気がします(間違っていたらご指摘ください)。
WAE-MMDでの式
Wasserstein Auto-Encodersの論文内ではまた違う式で表現しています。
k(x, y) = \frac{C}{C+||x - y||^2}
分母に平方根がありませんね…Wikipediaの解説を見る限り、逆二乗カーネル(Inverse quadratic kernel)に見えます。
式変形をしてみましょう。
\frac{C}{C+r^2} = \frac{1}{1+\frac{r^2}{C}} \\
( \epsilon r)^2 = \frac{r^2}{C} \\
\epsilon^2 r^2 = \frac{r^2}{C} \\
\epsilon^2 = \frac{1}{C} \\
\epsilon = \sqrt{\frac{1}{C}}
$r^2 = ||x - y||^2$なので
k(x, y) = \frac{1}{1+(\epsilon r)^2}
と変換でき、よってこのカーネル関数はInverse Multiquadric kernelではなくInverse quadratic kernelが正しい気がします。
なお、WAE論文の原文では"In all experiments we used $C = 2_z\sigma^2_d$, which is the expected squared distance between two multivariate Gaussian vectors drawn from $P_Z$"とあります。
Cは確率分布$P_Z$由来の多変量ガウスベクトル2点間の距離の2乗、ということのようです。
ガウシアンカーネルの可視化
まずは"A Visual Exploration of Gaussian Process"のRBFガウシアンカーネルの可視化と同じような出力を出すことを考えてみましょう。
リアルタイムにインタラクティブな操作ができるところまでいきなり到達するのは難しそうなので、まずはjupyter notebookとmatplotlibで似たような図を出すことを考えます。
$k(x, y)$の値をそれぞれ-5 ~ 5の間で計算し、その値をヒートマップとして表示しているようなので、matplotlibのpcolormeshを使うことができそうです。
ガウシアンカーネルを関数として定義します。一般的には入力x, yはそれぞれベクトルですが、今回は可視化のためスカラ値を入力し、定義に沿って出力します。計算式は"A Visual Exploration of Gaussian Processes"に合わせてみます。
def rbfgaussian(x, y, length=0.8, sigma=0.8):
z = (sigma)**2 * np.exp(-((x - y)** 2/ (2 * length**2)))
return z
単純にX, Y = [0, 1, 2, 3, 4, 5]としたときの図を書いてみます。
X = list(range(5+1))
data = np.zeros((5+1, 5+1))
for x in X:
for y in X:
data[x, y] = rbfgaussian(x, y)
plt.pcolormesh(X, X, data, cmap='Blues')
plt.colorbar()
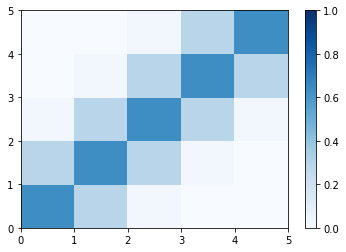
書きたい図と比べるとちょっと異なります。これはおそらく軸の方向がA Visual Exploration of Gaussian Processesとは逆になっているのではないかと思います。y軸を反転させてみましょう。
X = list(range(5+1))
data = np.zeros((5+1, 5+1))
for x in X:
for y in X:
data[x, y] = rbfgaussian(x, y)
plt.gca().invert_yaxis() # Y軸反転
plt.pcolormesh(X, X, data, cmap='Blues', vmin=0, vmax=1)
plt.colorbar()
それっぽくなってきました。
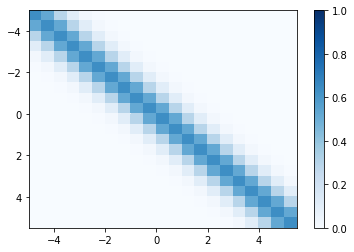
粒度を上げて、値の範囲も-5~5に変更し、描画するまでの処理を関数にしてみます。
def drawheatmap(max_xy, step, kfunc, **kwargs):
X = np.arange(-max_xy, max_xy+1, step)
chunks = X.shape[0]
data = np.zeros((chunks, chunks))
X = np.arange(-max_xy, max_xy+1, step)
for i, x in enumerate(X):
for j, y in enumerate(X):
data[i, j] = kfunc(x, y, **kwargs)
plt.gca().invert_yaxis()
plt.pcolormesh(X, X, data, cmap='Blues', vmin=0, vmax=1)
plt.colorbar()
描画させると以下のようになります。
drawheatmap(5, 0.5, rbfgaussian)
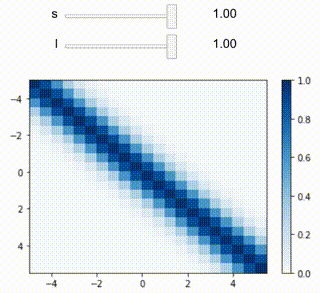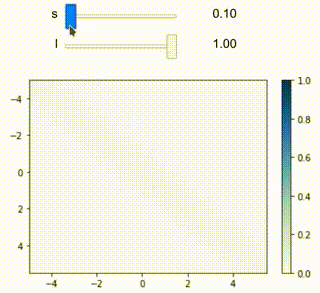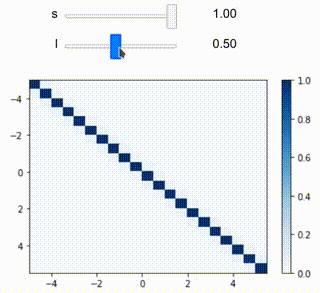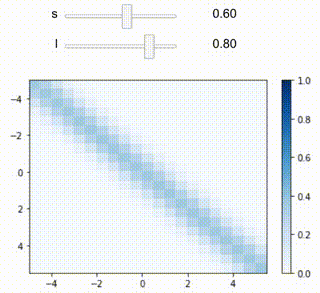
パラメータも変えてみましょう。sigmaを大きくすれば濃くなるはずです。
drawheatmap(5, 0.5, rbfgaussian, sigma=1)
インタラクティブに表示させる
もとのページではパラメータ$\sigma, l$がスライダーで変更できるようになっていたので、同じことをやらせます。ipywidgetsを使えばできそうです。
こちらの記事を参考にしました。ただ、この記事では古いモジュール名(IPython.html.widgets)を使っているので、ipywidgetsに読み替えます。
@interact(s=(0.1, 1), l=(0.1, 1))
def inter_rbf(s, l):
drawheatmap(5, 0.5, rbfgaussian, sigma=s, length=l)
うっかり0除算しないように範囲を決める必要があります。
計算は基本jupyter notebookが動作している側でやることになりますが、件のページとだいたい同じようなことが再現できました。
IMQ kernelの可視化
既に計算を行う部分を関数化して定義しているので、その中身をIMQに置き換えれば、同じことができます。
def rbfimq(x, y, c=1):
z = 1 / np.sqrt((x-y)**2 + c**2)
return z
@interact(c=(0.01, 5))
def inter_rbf(c):
drawheatmap(5, 0.5, rbfimq, c=c)
ガウシアンカーネルと比較すると、色の濃い(値の大きい)領域がより太くなっている傾向が見られます。また、Cを1より大きくすると全体的に薄くなっていくことが確認できます。
WAE-MMDでの式
おそらくはIMQではなくInverse quadraticだと思われる、WAE論文の式を可視化してみます。
def rbfwaeimq(x, y, c=1):
z = c / (c + (x-y)**2)
return z
@interact(c=(0.01, 5))
def inter_rbf(c):
drawheatmap(5, 0.5, rbfwaeimq, c=c)
$x = y$の時は常に$C/C = 1$となるので、その領域は色が濃くなっています。Cを1より大きくすると色の濃いエリアが広がる傾向が見られます。
やはりWAEのカーネル関数はIMQではないのでは…との思いが強くなります。
線形カーネル
せっかくなので線形カーネルでもやってみましょう。
def linear(x, y, c = 0, sigma=0.3, sigmab=0.8):
z = sigmab**2 + sigma **2 * (x - c) * (y - c)
return z
@interact(c=(-1.5, 1.5), sigma=(0.01, 1), sigmab=(0.1, 1))
def inter_rbf(c, sigma=0.34, sigmab=0.8):
drawheatmap(5, 0.5, linear, c=c, sigma=sigma, sigmab=sigmab)
最後に
可視化をしてみることで理解を深めることができました。世の中の解説は微妙に式が違うことがあり、式変形を自分でやってみることも重要である、という気づきを個人的には得られました。
しかしどうせなら、A Visual Exploration of Gaussian Processesと同じようにすべてクライアントサイドで完結するような方法でも実装してみたいものです。