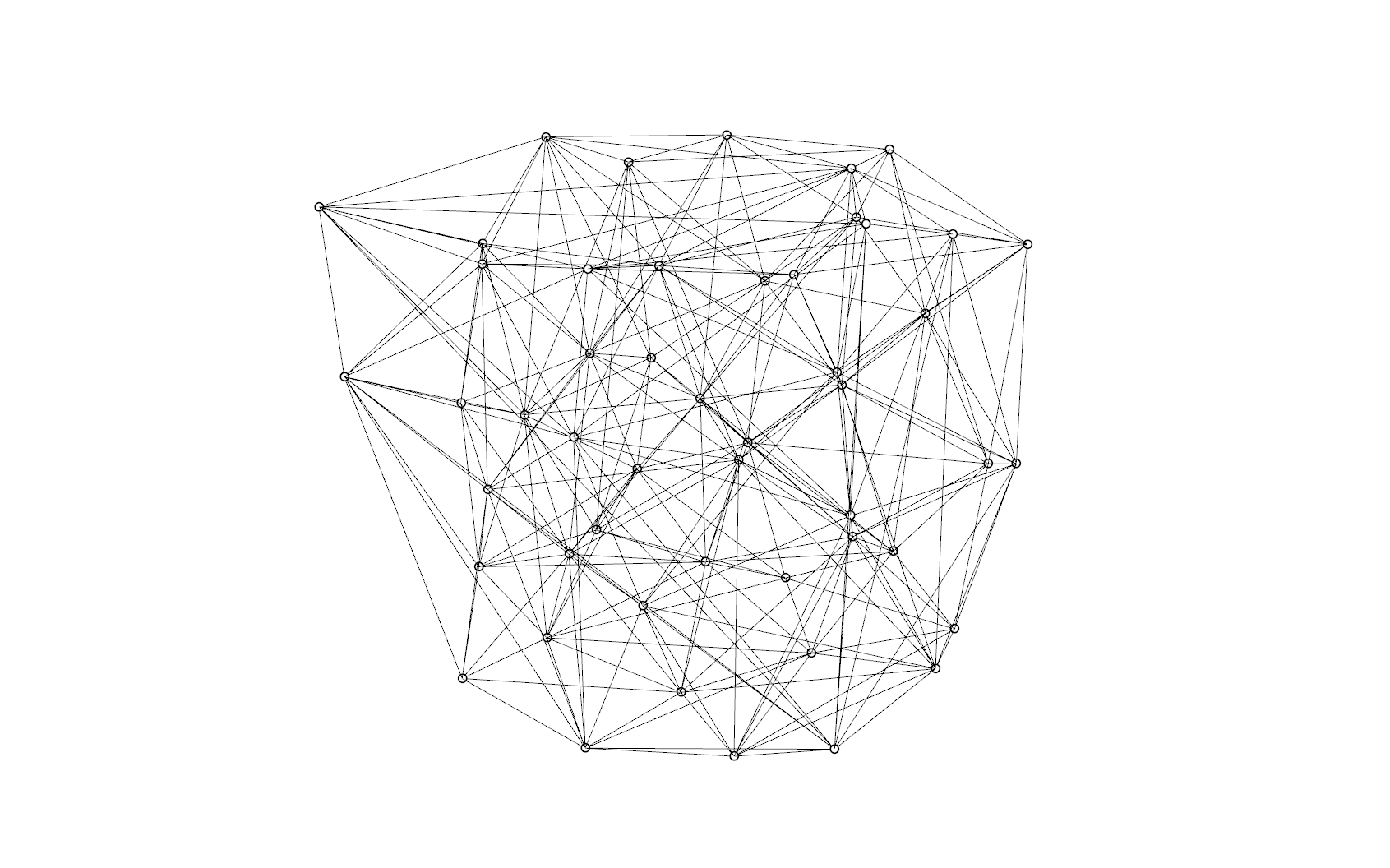
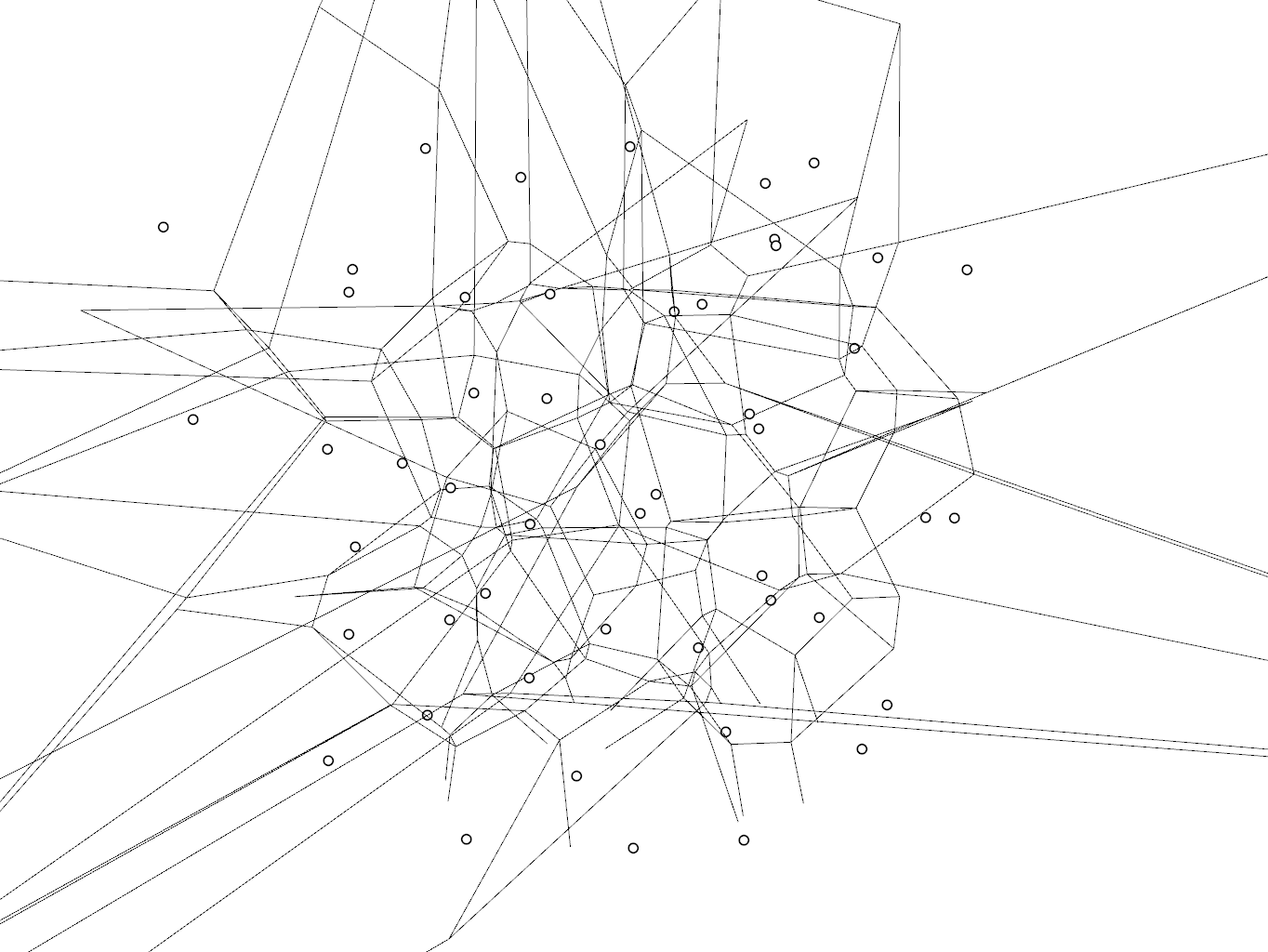
3次元ドロネー分割とボロノイ分割を実装してみた。

3次元ドロネー分割とボロノイを実装してみた。

はじめに

以前に２次元ドロネーとボロノイの実装を行いましたが、今回はその発展版ということで３次元ドロネー分割とボロノイ分割の実装をおこないました。（以前の記事はこちら)
自前の実装になっておりますので、不備等あるかもしれませんが、参考になれば幸いです。

描画環境にRhinocerosという3DCADソフトを使用していますが、入力と出力以外は依存しないように記述していますので、他の環境での応用可能であると思います。

まずはドロネー分割から

今回はまずドロネー分割を行った後にボロノイ分割を行うという工程ですすめていきます。

ファイルの構造ですが、以下のようになっております。

root/
├ Main.py
├ voronoi_module/
│ ├ Point.py
│ └ Tetrahedron.py

はじめにRhinoceros上で作成した点群を取得しPointクラスのインスタンスを作成します。

Main.py

# coding: utf-8
import rhinoscriptsyntax as rs
from voronoi_module import Tetrahedron
from voronoi_module import Point


points_obj_list = []  # Pointのオブジェクトを保持。
divide_tetrahedron_list = []  # このリストに三角形分割を保持していく。[p1, p2, p3]


# Rhino上の点群を取得し座標値を取得。
points = rs.GetObjects('select points to use 3D Delaunay', rs.filter.point)

for i in range(len(points)):
    point = Point.Point(points[i])
    point.system_guid_obj_to_coordinate()
    points_obj_list.append(point)

この部分は僕がRhinoを入力、出力環境として使用しているのでこのようになっていますが、p = [x, y, z]のように対応するリストを作成することで代替可能です。

因みにPointクラスは以下のような構成になっています。

Point.py

# coding: utf-8
import rhinoscriptsyntax as rs


class Point:
    def __init__(self, point):
        self.point = point
        self.x = None
        self.y = None
        self.z = None
        self.coordinate = None

    def system_guid_obj_to_coordinate(self):
        '''System.GuidObjectをRhino.Objectに変換。クラス変数に座標値を保持させる'''

        p = rs.coerce3dpoint(self.point)
        self.x = p[0]
        self.y = p[1]
        self.z = p[2]
        self.coordinate = [p[0], p[1], p[2]]

    def change_coordinate(self):
        '''外接円を構成する点を変換するメソッド'''

        p = self.point
        self.x = p[0]
        self.y = p[1]
        self.z = p[2]
        self.coordinate = [p[0], p[1], p[2]]

def system_guid_obj_to_coordinate(self):はRhinoで取得したデータを変換するための関数ですので、Rhinoを使用しない場合必要ありません。

続いてドロネー分割のメインアルゴリズムです。
1. 作成した点群を内包するような四面体を作成
2. 作成した四面体の外接球を計算
3. 外接球内にある点群の内、任意の一点を追加する。
4. 追加した点を使用して外接球が属している四面体を四面体分割する。
5. 2~4を繰り返す。

ことでドロネー三角分割を実現できます。（ざっくりな説明なのですが。。。

以下コードです。

Main.py

# ドロネー分割の前準備。
# はじめの外接円を構成する点のインスタンス作成。この範囲内に点群を収めておく必要あり。
p1 = Point.Point([0, 0, 800])
p1.change_coordinate()
p2 = Point.Point([0, 1000, -200])
p2.change_coordinate()
p3 = Point.Point([866.025, -500, -200])
p3.change_coordinate()
p4 = Point.Point([-866.025, -500, -200])
p4.change_coordinate()

tetrahedron = Tetrahedron.Tetrahedron(p1, p2, p3, p4)
tetrahedron.cul_center_p_and_radius()
divide_tetrahedron_list.append(tetrahedron)


# ドロネー分割のメインアルゴリズム
# for _ in range(len(points_obj_list)):
for _ in range(len(points_obj_list)):

    # 追加するポイントの選択。
    select_point = points_obj_list.pop(0)

    # 三角形の外接円内に追加したポイントが内包されていないか判定。内包されている場合はindexを保存。
    temp_divide_tetrahedron = []
    count = 0
    for i in range(len(divide_tetrahedron_list)):
        tri = divide_tetrahedron_list[i + count]
        check = tri.check_point_include_circumsphere(select_point)
        if check:
            # 内包していた三角形の頂点を使用して再分割する。
            new_tetrahedron1 = Tetrahedron.Tetrahedron(tri.p1, tri.p2, tri.p3, select_point)
            new_tetrahedron2 = Tetrahedron.Tetrahedron(tri.p1, tri.p2, tri.p4, select_point)
            new_tetrahedron3 = Tetrahedron.Tetrahedron(tri.p1, tri.p3, tri.p4, select_point)
            new_tetrahedron4 = Tetrahedron.Tetrahedron(tri.p2, tri.p3, tri.p4, select_point)
            new_tetrahedron1.cul_center_p_and_radius()
            new_tetrahedron2.cul_center_p_and_radius()
            new_tetrahedron3.cul_center_p_and_radius()
            new_tetrahedron4.cul_center_p_and_radius()

            temp_divide_tetrahedron.append(new_tetrahedron1)
            temp_divide_tetrahedron.append(new_tetrahedron2)
            temp_divide_tetrahedron.append(new_tetrahedron3)
            temp_divide_tetrahedron.append(new_tetrahedron4)

            del divide_tetrahedron_list[i + count]
            count = count - 1
        else:
            pass

    # 重複している三角形を削除
    del_instances = []
    for tetra in temp_divide_tetrahedron:
        for tetra_check in temp_divide_tetrahedron:
            if tetra == tetra_check:
                continue
            if tetra.radius == tetra_check.radius and tetra.center_p == tetra_check.center_p:
                del_instances.append(tetra_check)
                del_instances.append(tetra)

    for del_instance in del_instances:
        if del_instance in temp_divide_tetrahedron:
            del temp_divide_tetrahedron[temp_divide_tetrahedron.index(del_instance)]

    # 重複三角形を削除した後にappend
    divide_tetrahedron_list.extend(temp_divide_tetrahedron)


# はじめに作成した四面体の母点をもつ四面体分割を削除
del_instances = []
for tetra_check in divide_tetrahedron_list:
    if tetra_check.p1 == p1 or tetra_check.p1 == p2 or tetra_check.p1 == p3 or \
            tetra_check.p1 == p4 or tetra_check.p2 == p1 or tetra_check.p2 == p2 or \
            tetra_check.p2 == p3 or tetra_check.p2 == p4 or tetra_check.p3 == p1 or \
            tetra_check.p3 == p2 or tetra_check.p3 == p3 or tetra_check.p3 == p4 or \
            tetra_check.p4 == p1 or tetra_check.p4 == p2 or tetra_check.p4 == p3 or \
            tetra_check.p4 == p4:
        del_instances.append(tetra_check)

for del_instance in del_instances:
    if del_instance in divide_tetrahedron_list:
        del divide_tetrahedron_list[divide_tetrahedron_list.index(del_instance)]


# ドロネー描画
for i in range(len(divide_tetrahedron_list)):
    divide_tetrahedron_list[i].draw_divide_tetrahedron()

今回は外接球を求める計算式を実装するのにつまずきました。。。
外接球に関しては別記事に後日まとめようと思います。。。

ちなみにTetrahedronクラスは以下のようになっています。

Point.py

# coding: utf-8
import math
import scriptcontext
import Rhino


class Tetrahedron:

    def __init__(self, p1, p2, p3, p4):
        self.p1 = p1
        self.p2 = p2
        self.p3 = p3
        self.p4 = p4
        self.radius = None
        self.center_p = None

    def cul_center_p_and_radius(self):
        '''外接球の中心点と半径を計算'''

        a = [
            [self.p1.x, self.p1.y, self.p1.z, 1],
            [self.p2.x, self.p2.y, self.p2.z, 1],
            [self.p3.x, self.p3.y, self.p3.z, 1],
            [self.p4.x, self.p4.y, self.p4.z, 1]
        ]

        d_x = [
            [pow(self.p1.x, 2) + pow(self.p1.y, 2) + pow(self.p1.z, 2), self.p1.y, self.p1.z, 1],
            [pow(self.p2.x, 2) + pow(self.p2.y, 2) + pow(self.p2.z, 2), self.p2.y, self.p2.z, 1],
            [pow(self.p3.x, 2) + pow(self.p3.y, 2) + pow(self.p3.z, 2), self.p3.y, self.p3.z, 1],
            [pow(self.p4.x, 2) + pow(self.p4.y, 2) + pow(self.p4.z, 2), self.p4.y, self.p4.z, 1]
        ]

        d_y = [
            [pow(self.p1.x, 2) + pow(self.p1.y, 2) + pow(self.p1.z, 2), self.p1.x, self.p1.z, 1],
            [pow(self.p2.x, 2) + pow(self.p2.y, 2) + pow(self.p2.z, 2), self.p2.x, self.p2.z, 1],
            [pow(self.p3.x, 2) + pow(self.p3.y, 2) + pow(self.p3.z, 2), self.p3.x, self.p3.z, 1],
            [pow(self.p4.x, 2) + pow(self.p4.y, 2) + pow(self.p4.z, 2), self.p4.x, self.p4.z, 1]
        ]

        d_z = [
            [pow(self.p1.x, 2) + pow(self.p1.y, 2) + pow(self.p1.z, 2), self.p1.x, self.p1.y, 1],
            [pow(self.p2.x, 2) + pow(self.p2.y, 2) + pow(self.p2.z, 2), self.p2.x, self.p2.y, 1],
            [pow(self.p3.x, 2) + pow(self.p3.y, 2) + pow(self.p3.z, 2), self.p3.x, self.p3.y, 1],
            [pow(self.p4.x, 2) + pow(self.p4.y, 2) + pow(self.p4.z, 2), self.p4.x, self.p4.y, 1]
        ]

        a = dit_4(a)
        d_x = dit_4(d_x)
        d_y = -(dit_4(d_y))
        d_z = dit_4(d_z)

        center_p_x = d_x / (2 * a)
        center_p_y = d_y / (2 * a)
        center_p_z = d_z / (2 * a)

        self.center_p = [float(center_p_x), float(center_p_y), float(center_p_z)]

        distance = math.sqrt(
            pow((self.p1.x - self.center_p[0]), 2) + pow((self.p1.y - self.center_p[1]), 2) + pow((self.p1.z - self.center_p[2]), 2))

        self.radius = float(distance)

    def draw_divide_tetrahedron(self):
        '''分割四面体をRhinoに描画するためのメソッド'''
        line1 = Rhino.Geometry.Line(self.p1.x, self.p1.y, self.p1.z, self.p2.x, self.p2.y, self.p2.z)
        line2 = Rhino.Geometry.Line(self.p1.x, self.p1.y, self.p1.z, self.p3.x, self.p3.y, self.p3.z)
        line3 = Rhino.Geometry.Line(self.p1.x, self.p1.y, self.p1.z, self.p4.x, self.p4.y, self.p4.z)
        line4 = Rhino.Geometry.Line(self.p2.x, self.p2.y, self.p2.z, self.p3.x, self.p3.y, self.p3.z)
        line5 = Rhino.Geometry.Line(self.p2.x, self.p2.y, self.p2.z, self.p4.x, self.p4.y, self.p4.z)
        line6 = Rhino.Geometry.Line(self.p3.x, self.p3.y, self.p3.z, self.p4.x, self.p4.y, self.p4.z)

        scriptcontext.doc.Objects.AddLine(line1)
        scriptcontext.doc.Objects.AddLine(line2)
        scriptcontext.doc.Objects.AddLine(line3)
        scriptcontext.doc.Objects.AddLine(line4)
        scriptcontext.doc.Objects.AddLine(line5)
        scriptcontext.doc.Objects.AddLine(line6)

    def check_point_include_circumsphere(self, check_p):
        '''外接球に任意の点が内包されているかどうか判定'''

        distance = math.sqrt(pow((check_p.x - self.center_p[0]), 2) + pow(
            (check_p.y - self.center_p[1]), 2) + pow((check_p.z - self.center_p[2]), 2))

        if distance < self.radius:
            return True
        else:
            return False


def dit_2(dit):
    '''二次元行列の計算'''
    cul = (dit[0][0] * dit[1][1]) - (dit[0][1] * dit[1][0])

    return cul


def dit_3(dit):
    '''三次行列の計算'''
    a = [
        [dit[1][1], dit[1][2]],
        [dit[2][1], dit[2][2]]
    ]

    b = [
        [dit[0][1], dit[0][2]],
        [dit[2][1], dit[2][2]]
    ]

    c = [
        [dit[0][1], dit[0][2]],
        [dit[1][1], dit[1][2]]
    ]

    cul = (dit[0][0] * dit_2(a)) - (dit[1][0] * dit_2(b)) + (dit[2][0] * dit_2(c))

    return cul


def dit_4(dit):
    '''4次元の行列'''
    a = [
        [dit[1][1], dit[1][2], dit[1][3]],
        [dit[2][1], dit[2][2], dit[2][3]],
        [dit[3][1], dit[3][2], dit[3][3]]
    ]

    b = [
        [dit[0][1], dit[0][2], dit[0][3]],
        [dit[2][1], dit[2][2], dit[2][3]],
        [dit[3][1], dit[3][2], dit[3][3]]
    ]

    c = [
        [dit[0][1], dit[0][2], dit[0][3]],
        [dit[1][1], dit[1][2], dit[1][3]],
        [dit[3][1], dit[3][2], dit[3][3]]
    ]

    d = [
        [dit[0][1], dit[0][2], dit[0][3]],
        [dit[1][1], dit[1][2], dit[1][3]],
        [dit[2][1], dit[2][2], dit[2][3]]
    ]

    cul = (dit[0][0] * dit_3(a)) - (dit[1][0] * dit_3(b)) + (dit[2][0] * dit_3(c)) - (dit[3][0] * dit_3(d))

    return cul

これみてなぜnumpy使って行列計算しないんだ！とツッコミキそうですがその通りです。。
今回は実行環境の問題でnumpyを使用することができなかったため行列計算が自前になってしまっています。。。。

最後にボロノイ分割

ボロノイ分割は外形を作成しトリミングなりしないと拡散してしまいます。
今回はトリミングのコードは実装していません。。。

以下のコードを追加することでボロノイ分割を実現できます。

Point.py

# ボロノイ分割。
for i in range(len(divide_tetrahedron_list)):
    tri_1 = divide_tetrahedron_list[i]
    for j in range(len(divide_tetrahedron_list)):
        if i == j:
            continue
        tri_2 = divide_tetrahedron_list[j]

        count = 0
        if tri_1.p1 == tri_2.p1 or tri_1.p1 == tri_2.p2 or tri_1.p1 == tri_2.p3 or tri_1.p1 == tri_2.p4:
            count += 1
        if tri_1.p2 == tri_2.p1 or tri_1.p2 == tri_2.p2 or tri_1.p2 == tri_2.p3 or tri_1.p2 == tri_2.p4:
            count += 1
        if tri_1.p3 == tri_2.p1 or tri_1.p3 == tri_2.p2 or tri_1.p3 == tri_2.p3 or tri_1.p3 == tri_2.p4:
            count += 1
        if tri_1.p4 == tri_2.p1 or tri_1.p4 == tri_2.p2 or tri_1.p4 == tri_2.p3 or tri_1.p4 == tri_2.p4:
            count += 1

        if count == 3:
            line = Rhino.Geometry.Line(tri_1.center_p[0], tri_1.center_p[1], tri_1.center_p[2], tri_2.center_p[0],
                                       tri_2.center_p[1], tri_2.center_p[2])
            scriptcontext.doc.Objects.AddLine(line)

まとめ

最後まで目を通していただきありがとうございました。自前での実装を通して計算機科学の分野は奥が深い。。と痛感しました。
自前でアルゴリズムを実装することと既存ライブラリを使用することのバランスは大切だなとも思った次第です。笑