はじめに
公開鍵を使ったデジタル署名にはRSA署名の他に、DSA(Digital Signature Algorithm)やそれを楕円曲線暗号の世界で実現したECDSAなどがあります。RSA署名に関しては難しい数学を使わないわかりやすい直感的な解説が多数存在しています。ところが、DSAに関してはわたしのような数学弱者エンジニアにとっては相当難解な解説ばかり。頼みのWikipediaでさえこんな感じです。
そういうわけで、今回は世界初。難しい数学の知識なしに直感的にDSAがわかったと思えるような解説に挑戦です!
DSAはRSAに比べていくつか弱点もあってあまり使用されていないのが現状ですが、楕円曲線暗号の世界ではEC-RSAのような署名アルゴリズムは存在しません。そのためDSAと同様の原理で実現されているECDSAやEdDSAは楕円曲線暗号による署名としては幅広く実用的に利用されています。そういう観点で、DSAの原理についてもある程度理解しておくことはあながち無駄ではないような気がします。
- RSAとDSAは原理的に何が違うの?
- DSAでは何を根拠に署名が正しいことを判断しているの?
などと言った素朴な疑問の解として、直感的なわかった感を味わっていただければ大成功です。
1. RSAとDSAの原理的な違い
RSA署名ではメッセージのハッシュを署名鍵を使って署名を生成し、検証の際は検証鍵を使ってその値にもどることを確認する、という方法がとられています。このように元に戻るような演算の組が存在しているものを「落とし戸付き一方向性関数」と呼ぶそうです。しかし、DSAではそのような性質の関数は利用しません。DSAでは、二つの異なる一方向演算の組み合わせ同士で同一の値を得ることができることを利用します。
2. 一方向演算の組合わせ
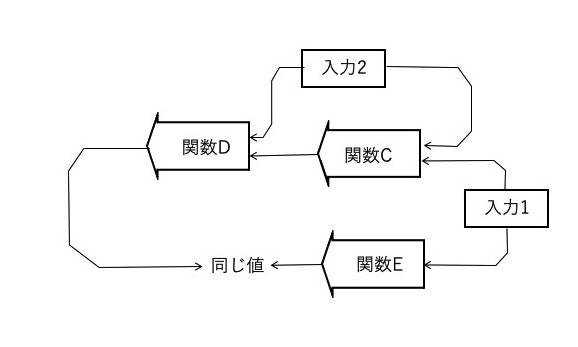
図のように関数CとDの2入力の関数と関数Eのような1入力の関数を考えます。このような関数の組み合わせで関数Cと関数Eに同じ入力1を、そして関数CとDに同じ入力2を加えると関数DとEが同じ結果となるようなうまい関数を作り出すのです。
これは一方向関数でなくて良いということなら、そんなに難しいことではありません。入力1をx、入力2をyとすれば、例えばこんな感じでどうでしょう。
関数C: x + y、 関数D:(x - y)^{2}
関数E: x^2
つまり、関数CとDの中に入力2を打ち消すような演算を入れておけばいいということに気がつきます。関数cで足されたyは関数Dで引かれるので、値は当然もとにもどります。
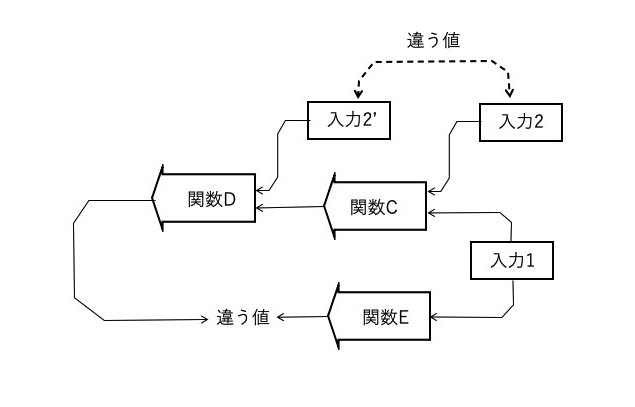
前の図ではC、Dとも同じ入力2が与えられていましたが、次の図のようにもし仮にC,Dの入力2に異なる値が与えられた場合はうまく打ち消しあわないことになります。関数Dと関数Eの結果は当然違う値になるはずですよね。
ここまで理解できたら、DSAの説明準備完了です。
3. 署名、検証フローを当てはめる
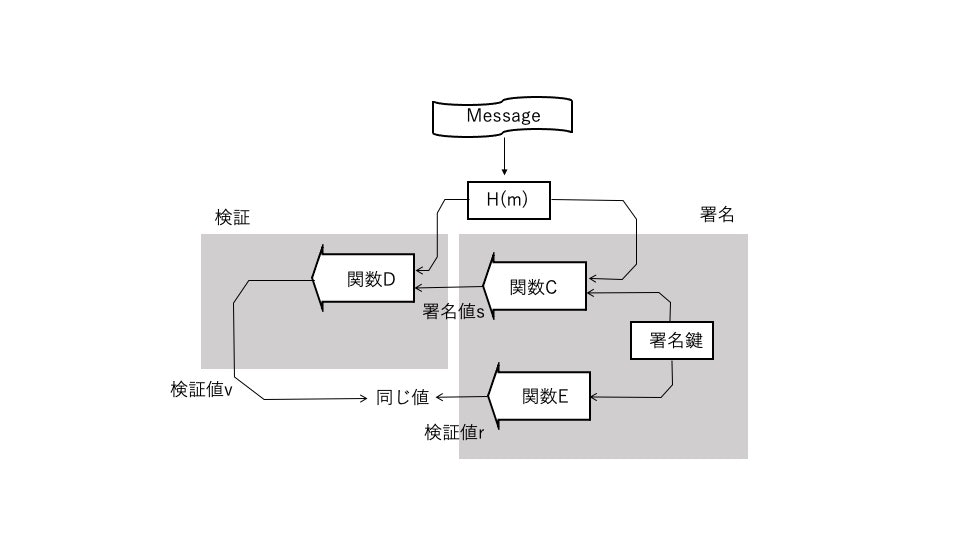
では、これを署名検証の流れに当てはめてみましょう。前の図の入力1は署名のための鍵です。入力2は署名対象のメッセージのハッシュ値です。DSAでは署名は署名値sと検証値rの二つの値の組み合わせとなります。関数Cの結果が署名値s、関数Eの結果が検証値rです。このよう当てはめると下の図のようになって、図の右半分が署名、左半分が検証の流れとなっていることがわかります。
署名側と検証側でH(m)が同じ値ならば、検証値vとrは同じ値となります。
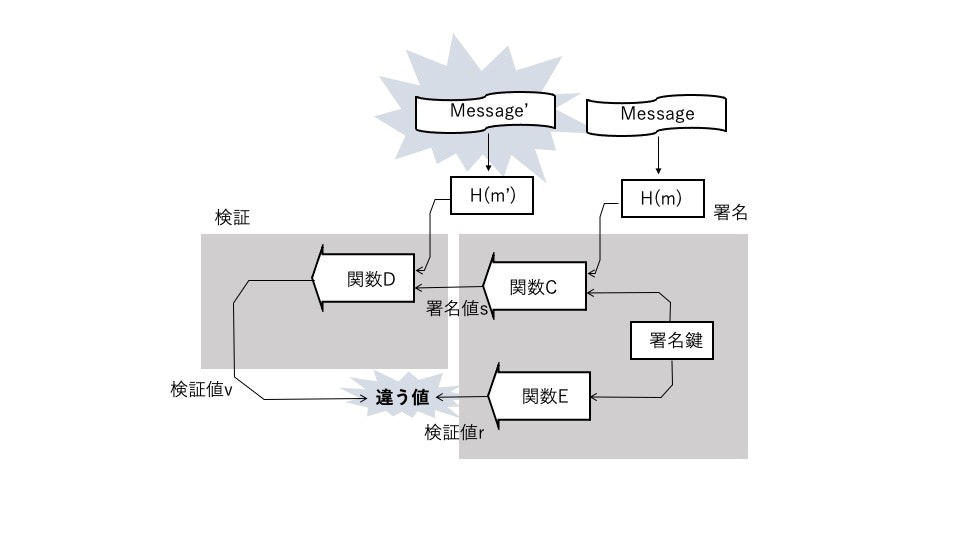
もし、例えばメッセージが改ざんされていて検証側のH(m)が署名側と異なれば検証値は一致しません。これで、署名の正当性が検証できたことになります。
もちろん、本物のデジタル署名では、上の例のような演算ではもとの鍵を簡単に逆算できてしまうので使えません。しかし、署名が正しいかどうかの判定について直感的にざっくり言えば、こんな感じで行われているのです。
4. DSAの演算式を当てはめる
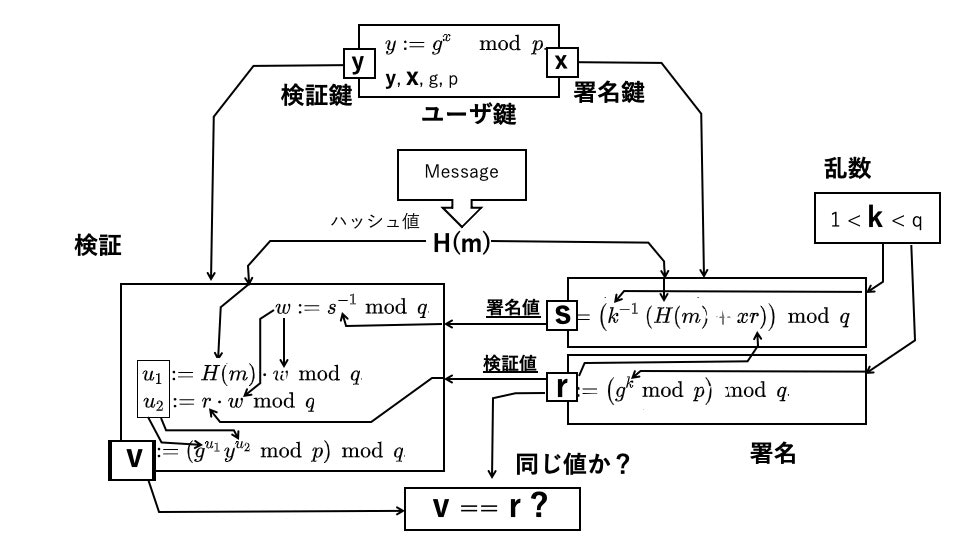
最後に、この図にDSAの実際の演算式を当てはめてみると下の図のようになります。
一方向演算を実現するためのパラメータとしてユーザ鍵ペアが加えられていたり、署名値rも検証演算に加えられていたり詳細の追加はありますが、基本的な構造は前の図と変わらないことがわかります。数学的厳密な意味は別として、随所に整数による公開鍵演算のプリミティブである冪乗の剰余が使われ一方向性が実現されていることを直感的に感ることができるかと思います(modは剰余を表します)。
DSAでは、このような形で「落とし戸付き一方向性関数」の性質を利用しないRSAとは異なる演算構造で署名、検証を実現しています。
まとめ
以上、専門家がみたらお笑いか激怒の超乱暴な説明ではありますが、少しでもアハー感を味わっていただけたら大成功です。まだまだ、わかりにくかった点、改善点などあるかと思います。感想、フィードバックお待ちしまています。
DSAは実現においては適切な鍵生成が難しく十分な注意が必要です。鍵を解読されないためには署名毎に新しい異なる乱数を生成する必要があります。また、検証のための計算量はRSAくらべてかなり大きくなる傾向にあります。そうした理由で、整数演算の世界においてはRSA署名のほうが広く利用されています。
しかし、楕円曲線暗号では「落とし戸付き一方向性関数」のようなものは見つかっていないため、RSAのような方法で署名検証を実現することはできません。整数演算の世界のDSAと等価のアルゴリズムを楕円曲線暗号の世界で実現したECDSA, EdDSAなどが広く使われています。