はじめに
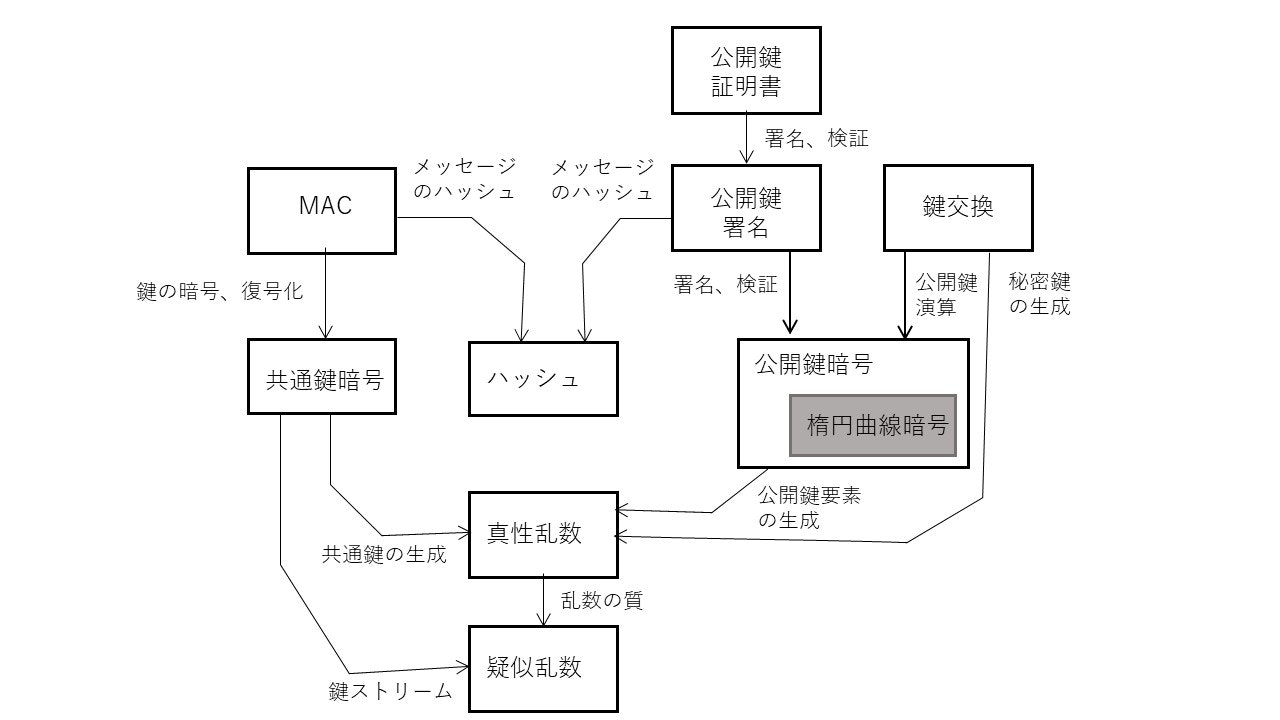
暗号技術は多岐にわたっていて、その関係をつかむのにいささか戸惑ってしまします。いまさらながらですが、 TLSで登場する暗号技術、アルゴリズムだけに絞ってまとめてみました。図は暗号技術要素とその関連を示したもので、矢印は技術要素の依存関係を示します。
この図に示すように、暗号アルゴリズムの多くが乱数の予測不能性に依存して組み立てられています。また、これらの暗号技術はハッシュ、共通鍵暗号、および公開鍵暗号の3つの要素技術と、それらを組み合わせた目的別の複合的な暗号技術とからできています。
1) 乱数
乱数はすべての近代暗号アルゴリズムの基本となるもので、その暗号強度は利用する乱数の質に依存しています。質の低い乱数を使用すると、例えば暗号化のための鍵の長さのようなものがが十分に生かされず秘匿性が確保されないことになるので十分な注意が必要です。
真性乱数は周期性や統計的な偏りがない純粋な乱数です。質の高い真性乱数を得ることは容易ではなく、特にソフトウェアのように決定論的に動作するアルゴリズムだけでは真性乱数を得ることはできません。疑似乱数は、もととなる乱数シード値を外部から与え周期が十分に長く統計的な偏りの少ない乱数列を決定論的に生成する技術です。擬似乱数は、質の高い真性乱数を直に生成するのが難しい場合に、真性乱数をシードとして擬似乱数を組み合わせて質の高い乱数を得るというような目的で使われす。擬似乱数はまた、シード値が同じ場合同一の乱数列を生成するので、例えばシミュレーションのように再現性が必要な応用でも利用されます。また、一つのマスター鍵から複数の目的別の鍵を生成する鍵導出や後述のストリーム暗号処理のための鍵の拡張なども擬似乱数の一種と言えます。
代表的な擬似乱数アルゴリズムとしては、Hash_DRBG, HMAC_DRBG, CTR_DRBGなどがあります。乱数の質に関する規定としては、例えば米国NISTによる SP 800-90A/B があります。
2) ハッシュ
ハッシュはメッセージダイジェストとも呼ばれ、不定長の長いメッセージを固定長の短いデータに圧縮するための一方向性のアルゴリズムです。データを圧縮するため異なるオリジナルメッセージから同一のハッシュ値が生成される(ハッシュ衝突の)可能性や、ハッシュ値からもとのメッセージを推測される(原像計算)リスクがあり、使用するアルゴリズムにはそうしたリスクが最小となることが求められます。
代表的なハッシュアルゴリズムとして、初期にはMD5, SHA1が広く使用されましたが危殆化のため現在ではSHA2(SHA256/384/512など)、SHA3などが標準化され使用されています。TLS1.3ではSHA2のSHA256/384が暗号スイートで使われるハッシュアルゴリズムとして採用されています。
3) 共通鍵暗号
暗号化と復号に同じ鍵を使用する暗号アルゴリズムを共通鍵暗号(対称鍵暗号)と呼びます。共通鍵暗号は大容量のデータを効率的に暗号化、復号できる特徴があるので、TLSではアプリケーションデータ転送時の暗号アルゴリズムとして使用します。
しかし、ネットワーク通信のように潜在的に多数の相手方と通信する可能性がある場合には、使用する鍵を相手方にどのように安全にわたすかという問題(鍵の配送問題)を抱えています。TLSでは、後述の公開鍵暗号の技術を使って通信の相手方と安全に同一の鍵を共有した上で(鍵交換、鍵合意)、共通鍵暗号によって暗号通信を行います。
共通鍵暗号はブロック単位に処理をするブロック型とそのような区切れを必要としないストリーム型にわけることができます。AESは現在ブロック型として一番広く使われているアルゴリズムです。また、ブロック型の場合ブロック間の情報の接続方法によって各種の利用モードがあります。AES-CBCはTLS1.2まではもっとも広く利用されていましたが、TLS1.3ではAES-GCM, AES-CCMのように暗号化と同時にメッセージが改ざんされたものでないこと(真正性)を検証できるものだけが標準として採用されています。
ストリーム型のアルゴリズムとして初期にはRC4が広く使われましたが危殆化により現在は廃止されています。TLS1.3ではChaCha 20がPoly1305によるメッセージ認証コードのアルゴリズムと組み合わされ標準として採用されています。
4) メッセージ認証コード(MAC)
ネットワーク通信においては受け取ったメッセージが改ざんされたものでないこと(完全性)の確認が課題となります。そのためのアルゴリズム、メッセージ認証コード(MAC)にはハッシュを利用したHMAC (Hash based MAC)、共通鍵暗号を利用したAES-MACなどがあります。MACによる検証には共通鍵がつかわれ鍵の正当な所有者だけがメッセージの完全性を検証するができます。
しかし、TLSにおいてはメッセージ認証はより細かな単位で行う必要性が高まりメッセージ認証は共通鍵暗号の一環として取り込まれるようになってきています(AEAD)。一方、鍵導出アルゴリズムでは従来はTLS独自のアルゴリズムが使われていましたが、TLS1.3ではMACアルゴリズムの一つであるHMACが採用されています。
5) 公開鍵による鍵交換と署名
当初、公開鍵暗号(非対称鍵暗号)は共通鍵の鍵配送問題解決のために研究されました。公開鍵アルゴリズムでは、暗号化、復号に異なる鍵を使用する暗号アルゴリズムで両者の鍵が異なり、暗号化のための鍵(公開鍵)を通信の相手方に渡して暗号化したメッセージを受け取ることができるからです。ただし、公開鍵暗号の処理は共通鍵暗号にくらべて極めて大きな処理時間がかかるため、TLSでは最初のハンドシェークで公開鍵による鍵交換で通信の両者が同一の鍵値を得たのち、それを共通鍵暗号の鍵として使用し、大量のメッセージを効率的に暗号化、複号するという手法がとられています。
初期のTLSではRSAによる暗号化、復号を利用した鍵交換方式が広く使用されていましたが、RSA方式では同じ鍵を長期に使いまわす必要がるため近年は公開鍵といえども秘匿性のリスクが指摘されてきました。そのため、元となる鍵の更新が容易なディフィーヘルマン(DH)型の鍵交換が推奨され、TLS1.3ではDH型の中でも楕円曲線暗号によるECDHEのみが標準として認められるに至っています。
公開鍵署名は、公開鍵暗号の特性である一方向性を利用したデジタル署名のアルゴリズムです。TLSでは、公開鍵署名は通信の相手方のなりすましを防ぐピア認証の手段として使われています。通信相手としての自分の正当性を証明するためには、まず自分の公開鍵の格納された証明書(後述)とともに、自分の署名用のプライベート鍵を使用して適当なメッセージ(Blob)に対する署名を送ります。受け取った側はBlobに対する署名が正しいものかどうかを証明書に格納された公開鍵で検証します。
代表的署名アルゴリズムにはRSA, DSAがあります。RSA署名ではRSA暗号化と同様、別の鍵を使ってデータを復元できる性質を使って署名検証を実現ますが、DSA署名では一方向演算の組合せだけで署名を検証します。DSAは署名のための運用に注意が必要な点があり処理時間的にも不利な点がありTLS1.3では採用されていません。しかし、同様の処理を楕円曲線暗号の世界で実現するECDSAが標準として採用されています。
このように公開鍵暗号の用途は当初の目的より大きく広がり、単純な情報秘匿化のための暗号化技術という色合いは薄れてきています。
6) 楕円曲線暗号
楕円曲線暗号では楕円曲線上の点とそれに対するスカラー乗算を定義します。RSAやDHが離散対数の逆演算困難性をベースとするのに対して、楕円曲線暗号ではスカラー値が十分大きい場合、楕円上の点に対するスカラー乗算の逆方向の演算が困難となることを暗号化に利用します。ECDHでは、この楕円曲線上の演算を利用してディフィーヘルマンと同様の方法で通信する両者で安全に共通の鍵を得ることができます。楕円曲線暗号はデジタル署名のアルゴリズムとしても利用されています。楕円曲線による署名アルゴリズムとしてDSAの原理を楕円曲線暗号で実現したECDSAが標準化されています。
一般的に、楕円曲線暗号はRSAのような素数に依拠するアルゴリズムより短い鍵で同程度の暗号強度を得ることができます。楕円曲線暗号はアルゴリズムはやや複雑になりますが、鍵が短くべき乗演算が容易なこともあり現実のアルゴリズム実行時間としては所要時間が短くなる傾向にあります。NISTは初期に楕円曲線の標準化に取り組み通称NIST曲線と呼ばれる一連の曲線を標準化しました。欧州を中心としたSECGによる曲線ともマッピングがとられTLSでも標準として採用されています。
最近では、Curve25519, Curve448のような演算処理が単純化される特別な楕円曲線も研究され、TLS1.3でも標準の曲線として採用されています。
7) 公開鍵証明書
公開鍵証明書は公開鍵とその他のメタ情報格納したものに署名をしたものです。証明書への署名は通信の双方が信頼する認証局(CA:Certification Authority)が認証局のプライベート鍵を使用して署名します。通信を行おうとするものは、信頼するCAの証明書を使って相手から送られてきた証明書が認証局によって正当に署名された正当な証明書であることを確認できます。また、証明書に格納されている通信相手の公開鍵を使って通信相手の正当性を認証することができます。
公開鍵証明書の書式はITU X.509、またそのベースとなるデータ構造定義ASN.1、DERによって物理的構造が標準化されています。DERをBase64でテキスト形式に変換したPEM形式もファイルフォーマットとして広く利用されています。
この記事の内容を含めてTLプログラミングについて解説をまとめる機会をいただきました。興味のあるかたはご覧ください。徹底解剖 TLS 1.3 (翔泳社から 3/7刊行)。