この記事はBabylon.js Advent Calendar 2024の20日目の記事です。
はじめに
前回の記事で面積計算をやったよ!じゃあ次は体積だよね?ということで体積計算を可視化していくよ。
できたもの
Playground
https://playground.babylonjs.com/#A28FEN#1
メッシュの体積を計算する方法
体積の計算方法については、モデルの体積を計算する の解説がわかりやすいかなと思います。
やっていることとしては「メッシュを構築する三角形と原点とで構成される三角錐について符号付き体積を計算して合計する」みたいなことなんですが、まあ何が何やらですよね?解説を見てもやっぱり難しい!
2次元上の多角形の面積の計算方法を解説するよ
わかんないときは問題を簡単にしよう!ということで3次元から2次元にして考えるよ。つまり体積じゃなくて面積で考えてみる。
上記の体積の計算方法を面積に置き換えると、
「多角形を構成する辺」と「原点」とで構成される三角形について、
「符号付き面積」を計算して合計する
ということなんだけど、順に見ていこう。
「多角形を構成する辺」と「原点」とで構成される三角形
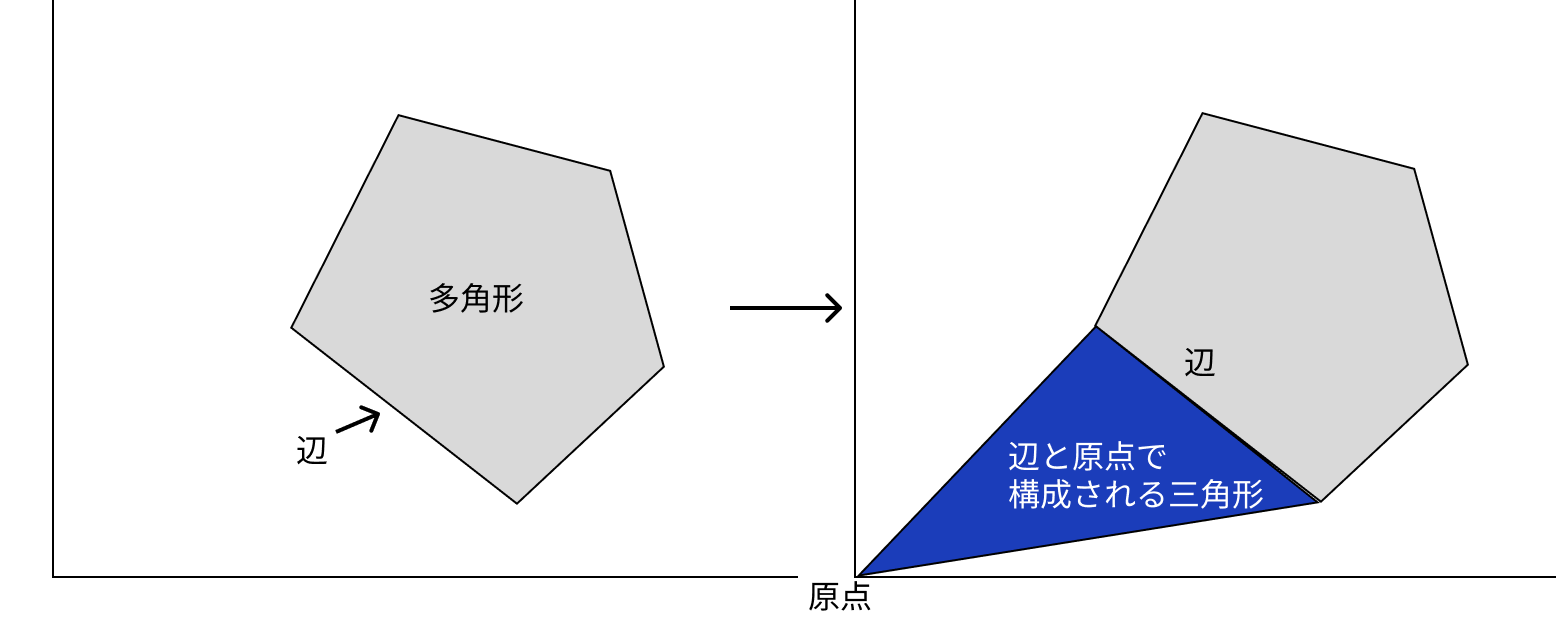
まずは最初の【「多角形を構成する辺」と「原点」とで構成される三角形】を図で表すとこんな感じ。
この図だと五角形だから5つの三角形を作ることができるね。この三角形の符号付き面積の和を計算するわけだ。
符号付き面積
でも「符号付き面積」って何?面積なんだからプラスの値しかないのでは...?って思うよね?その説明をするよ。
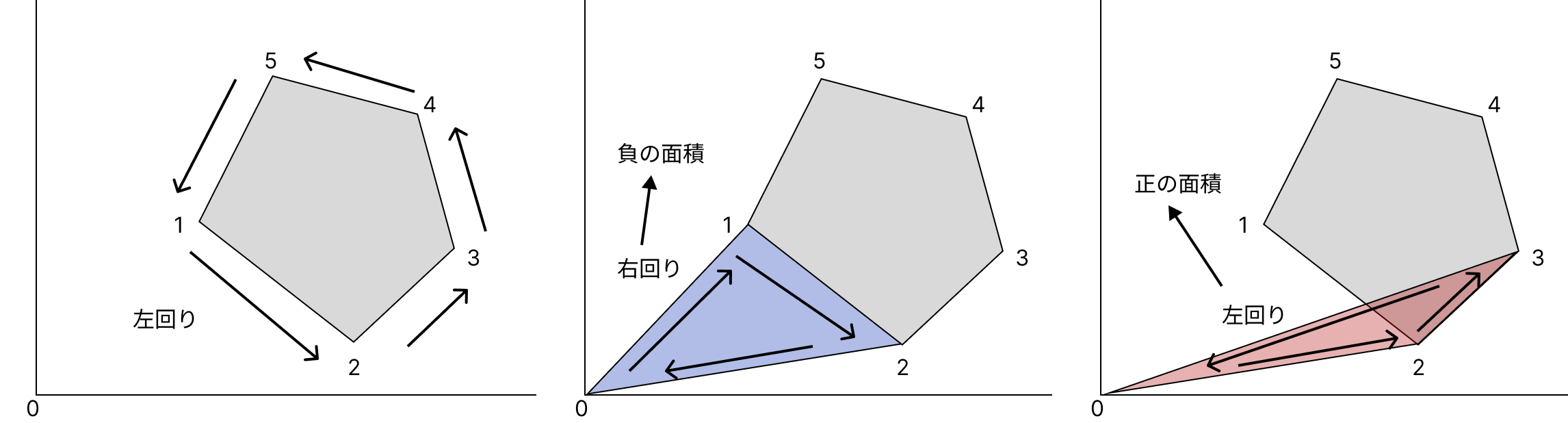
ここで、多角形の頂点から左回りに矢印を引いてみる。そしてその矢印を基準に三角形を見ると、(0, 2, 1)の三角形は右回り、(0, 2, 3)の三角形は左回りになっているね。
この左周り右回りの違いによって、面積の符号を変えるのが「符号付き面積」だよ。今回の場合だと、右回りになっている三角形の面積を負の面積、左回りになっている三角形の面積を正の面積、とするよ。
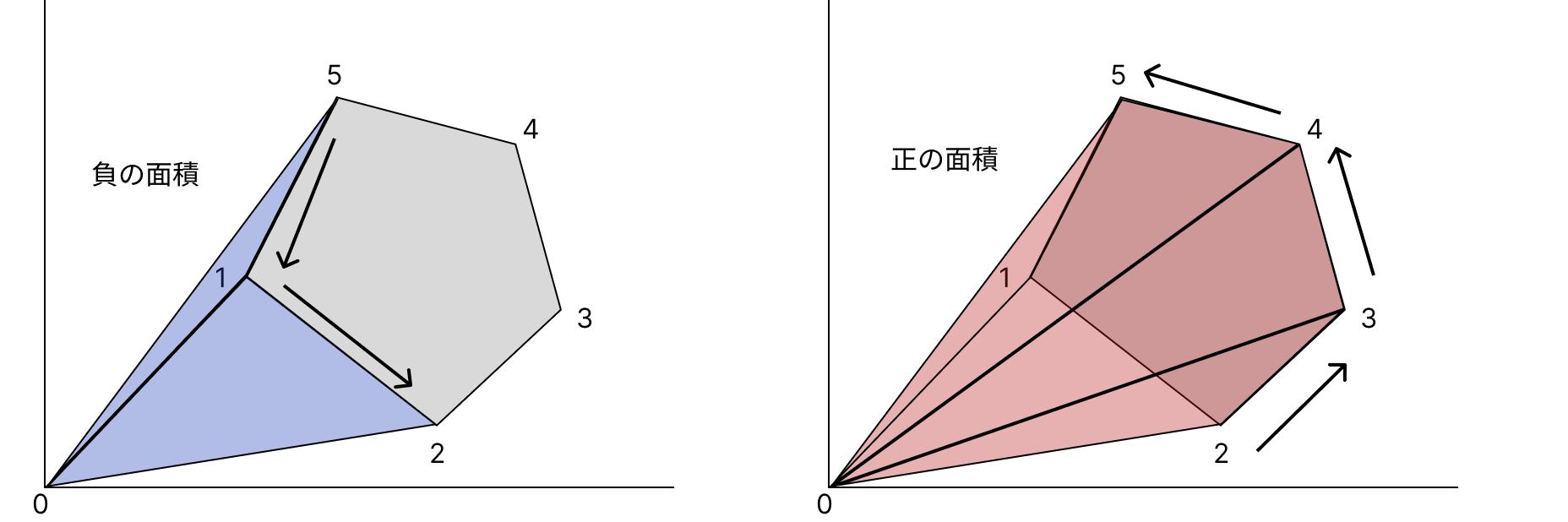
五角形の5つの三角形について図にすると以下のような感じ。青が負の面積、赤が正の面積になっているから、面積を足し合わせると多角形の面積になっていることがわかるね。
こんな感じに【「多角形を構成する辺」と「原点」とで構成される三角形について、「符号付き面積」を合計する】ことで、多角形の面積を計算できることがわかったね。
体積計算を可視化しよう!
さて、2Dがわかったから次は3Dだ!ということで改めて計算方法を確認してみると
「メッシュを構築する三角形」と「原点」とで構成される三角錐について、
「符号付き体積」を計算して合計する
この意味がイメージしやすくなっているんじゃないかと思う。じゃあこれを図で説明してみよう!と思うわけだけど、図にするの難しいよね?
そういうわけでBabylon.jsで可視化していこう!というのがこの記事の趣旨なんだけど...ここまで長かったね?
できました
なにか解説を書こうと思ったんだけど、
実際に説明を文章で書くよりも触ってもらったほうがわかりやすいでしょ!というかここまで読んでみんな疲れてるよ!あとはみんな実物触って遊ぶがいいさ!
と思ったのでPlaygroundに作ってあるからみんな遊んでね!別にここまで記事書いて力尽きたわけじゃないんだからね!?
※ 最初の方に乗せたのと同じリンクです
すっごく簡単にだけやっていることを説明すると
- メッシュから三角形を取得
- 三角形と原点で三角錐を作って面積を計算
- ボタンに応じて表示される三角錐と面積を切り替えるようにする
ということをやっているよ!
まとめ
メッシュの体積計算の方法を解説したよ!難しい問題を理解するためには、まずは問題を簡単にして考えるって大事だよね。
最後はサボったわけじゃないんです><
参考