Babylon.jsでメッシュの面積計算を可視化する

この記事はBabylon.js Advent Calendar 2024の18日目の記事です。

はじめに

前回の記事で、幅優先探索を行うことによってメッシュの三角形を徐々に塗りつぶす、ということを行いました。今回は深さ優先探索を用いることでメッシュの面の面積を計算します。

できたもの

コード

やっていること

今回の面積計算の処理は、

• クリックしたメッシュの三角形を開始位置として深さ優先探索を行い、
• 隣接している三角形の面積を順に計算して足し合わせる

という処理で計算を行っています。

つまり、前回の記事から以下を変更することで、メッシュの面積を計算することができます。

• 幅優先探索を深さ優先探索に変更
• 三角形の面積を計算する処理を追加

※ 幅優先探索でも計算できますが、深さ優先探索のほうが向いています。

深さ優先探索

深さ優先探索は以下のようなコードにしています。再帰関数にしているのでちょっとなれないと難しいですが、やっていることはシンプルかなと思います。
（深さ優先探索そのものの解説は、アルゴリズムの解説ページが色々あると思うのでそちらに譲ります。）

function animateTriangleFilling(startFaceId) {
    const visited = new Set();

    const visitColor = new BABYLON.Color3(0.84, 0.84, 0.84);
    async function dfs(faceId) {
        // 訪問済みの三角形はスキップ
        if (visited.has(faceId)) {
            return;
        }

        // 現在の三角形を訪問済みとしてマーク
        visited.add(faceId);

        // 現在の三角形を色変更
        setTriangleColor(faceId, visitColor);

        // 50ms待機
        await new Promise((resolve) => setTimeout(resolve, 50));

        // 隣接三角形を探索
        const neighbors = adjacencyList[faceId];
        for (const neighbor of neighbors) {
            if (!visited.has(neighbor)) {
                await dfs(neighbor); // 再帰的に訪問
            }
        }
    }

    dfs(startFaceId);
}

三角形の面積の計算

三角形の面積の計算は以下で行います。

// 三角形の面積を計算する関数
function calculateTriangleArea(v0, v1, v2) {
    const vector1 = v1.subtract(v0);
    const vector2 = v2.subtract(v0);
    const cross = BABYLON.Vector3.Cross(vector1, vector2);
    return 0.5 * cross.length();
}

なんでこれで計算できるのかは、高校数学とかの解説ページが色々あると思うのでそちらを見てもらえると。簡単に言うと 「底辺×高さ/2」の計算を三角関数とかを使って式変形するとこうなります。

面積計算を実装したPlayground

これらを実装したものが以下です。面積を画面に表示したり、どこを探索しているのかわかるようにしたりとかを色々追加しているので、ごちゃごちゃしていますがメインの処理は上記の深さ優先探索と面積計算です。これで面積が計算できました。

平面の面積を計算する

表面積の計算は実装できました。でもクリックした箇所の平面部分の面積が知りたいときもあると思います。

そんなわけで、次は平面の面積の計算を行ってみます。

隣接条件を変更する

平面の面積を計算すると言っても、表面積すべてを計算するときと処理はほとんど同じです。やることは隣接の条件を変えるだけです。
前回記事の隣接リストの作成 では「2頂点を共有していること」が隣接条件でした。これに加えて「三角形の面が同じ方向を向いていること」を条件に追加することで、平面の面積を計算することができます。

隣接判定はコードでいうと以下の部分です。ここの if文 に条件を追加してもいいのですが、後のことを考えて隣接リストに角度情報を追加することにします。

  // 隣接条件: 2つの頂点を共有している場合
  if (sharedVertexCount >= 2) {
      const triangleIndex2 = j / 3;
      if (!adjacencyList[triangleIndex1].includes(triangleIndex2)) {
+         const normal2 = calculateNormal(...triangle2);
+         const angle = calculateAngleBetweenVectors(normal1, normal2);
+         adjacencyList[triangleIndex1].push({ triangleIndex: triangleIndex2, angle });
-          adjacencyList[triangleIndex1].push(triangleIndex2);
      }
  }

作られるデータとしては以下のような形式です。
1つ目のデータであれば、0 の三角形に対して 1 の三角形が 0度で隣接、 6，11は90度で隣接している、という形式ですね。

{
    "0": [{"triangleIndex": 1, "angle": 0}, {"triangleIndex": 6, "angle": 90}, {"triangleIndex": 11, "angle": 90}],
    "1": [{"triangleIndex": 0, "angle": 0}, {"triangleIndex": 5, "angle": 90}, {"triangleIndex": 9, "angle": 90}],
    "2": [{"triangleIndex": 3, "angle": 0}, {"triangleIndex": 7, "angle": 90}, {"triangleIndex": 8, "angle": 90}],
    "3": [{"triangleIndex": 2, "angle": 0}, {"triangleIndex": 4, "angle": 90}, {"triangleIndex": 10, "angle": 90}],
    "4": [{"triangleIndex": 3, "angle": 90}, {"triangleIndex": 5, "angle": 0}, {"triangleIndex": 10, "angle": 90}],
    "5": [{"triangleIndex": 1, "angle": 90}, {"triangleIndex": 4, "angle": 0}, {"triangleIndex": 9, "angle": 90}],
    "6": [{"triangleIndex": 0, "angle": 90}, {"triangleIndex": 7, "angle": 0}, {"triangleIndex": 11, "angle": 90}],
    "7": [{"triangleIndex": 2, "angle": 90}, {"triangleIndex": 6, "angle": 0}, {"triangleIndex": 8, "angle": 90}],
    "8": [{"triangleIndex": 2, "angle": 90}, {"triangleIndex": 7, "angle": 90}, {"triangleIndex": 9, "angle": 0}],
    "9": [{"triangleIndex": 1, "angle": 90}, {"triangleIndex": 5, "angle": 90}, {"triangleIndex": 8, "angle": 0}],
    "10": [{"triangleIndex": 3, "angle": 90}, {"triangleIndex": 4, "angle": 90}, {"triangleIndex": 11, "angle": 0}],
    "11": [{"triangleIndex": 0, "angle": 90}, {"triangleIndex": 6, "angle": 90}, {"triangleIndex": 10, "angle": 0}],
}

探索時に隣接チェックを追加する

角度の情報が隣接リストに追加されたので、その情報を使って探索処理の方を修正します。といっても次の三角形を探索するときの条件に角度の条件を追加するだけです。

これで隣り合っていて、かつ、2つの三角形面のなす角度が0度の三角形のみが探索されるようになります。

  // 隣接三角形を探索
  const neighbors = adjacencyList[faceId];
  for (const neighbor of neighbors) {
+      const neighborIndex = neighbor.triangleIndex;
+      const neighborAngle = neighbor.angle;
+      if (!visited.has(neighborIndex) && neighborAngle <= 0) {
-      if (!visited.has(neighbor)) {
          await dfs(neighborIndex); // 再帰的に訪問
      }
  }

平面の面積計算を実装したPlayground

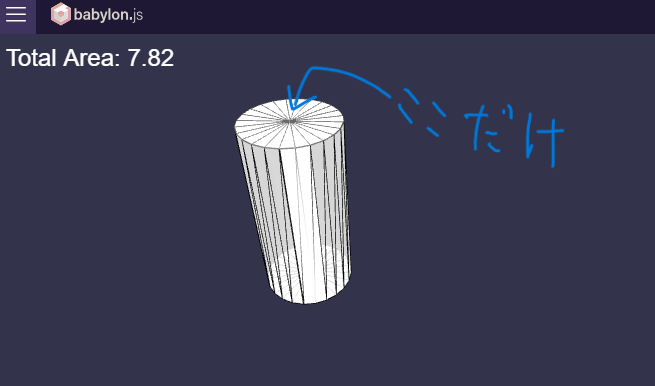
そんなわけでできあがりました。画像は円柱の上面を選択して計算した結果です。側面は色が塗られておらず、計算されていないことがわかります。（...若干色がわかりにくいけど）

曲面も計算したくない？したいよね？

でもでも？これ側面も計算したいよね？でもこれだとうまく計算できないじゃん！知りたいのはそうじゃないんだよ！！

ちゃんと側面を一周したときの面積を知りたいよー٩(๑`^´๑)۶

ある程度の角度の違いは許容しようぜ？

さっき平面を計算したときの角度の条件だと、こうしたと思うんだよ。

     if (!visited.has(neighborIndex) && neighborAngle <= 0) {

でもこれだと0度指定だから、ほんとに平面になっている部分しか隣接してないって判定されちゃうんだよね？だったらちょっとの角度の違いは許容して、曲面部分も隣接しているって判定させちゃおうぜ！

そういうわけでこうやって角度を変数で指定できるようにするよ。

    if (!visited.has(neighborIndex) && neighborAngle <= angleThreshold) {

これで曲面も計算できるね！

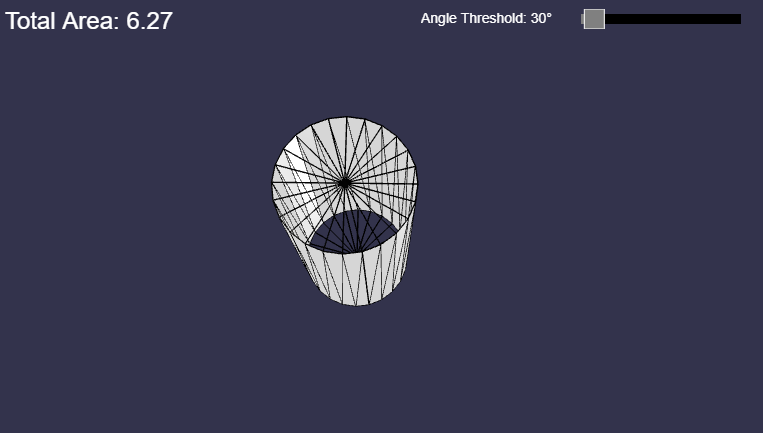
できたよやったー。こうやってスライダーを付けてUIから指定するようにすれば、表面積も平面も曲面も自由自在に計算できるぜ！やったね！

まとめ

そんなわけでメッシュの面積の計算方法を解説したよ！ついでにどうやって探索しているのかを色を変えて可視化してみたよ。探索アルゴリズムって面白いね？

ちなみに途中で真面目に書くのに飽きました。テンションが変わるなんて、まあよくあることだと思います。しかたないね！