お疲れ様です!
きうちです^^
今日は、フラクタル図形のお話をします。
あ、ソースはJavaのものを載せてありますが、
例によってC#版とVB.NET版もすぐに追加で載せようと思っています。
.NET派の方も、請うご期待♪
あこがれの「綺麗な図形」
自分が中学のころ、よくパソコン雑誌を読み漁っていました。
当時はインターネットなんてなかったので、雑誌が有益な情報源でした。
そして、そうした雑誌でときおり見かける「なんとも綺麗な図形」、それがフラクタル図形でした。
それをプログラムで描けるのだ、と知った時、
「自分もこういうのを描くプログラムを作ってみたい!」
そう思ったものです。
言うなれば、自分がパソコン&プログラム大好きになったひとつの理由ですね。
フラクタル図形とその例
フラクタル図形というのは、
「図形の部分と全体が自己相似になっている」ような図形です。
この説明だと「なんのこっちゃ」ですね。
言い換えると、「あるものの集まりが、その『あるもの』の形になっている」そんな図形です。
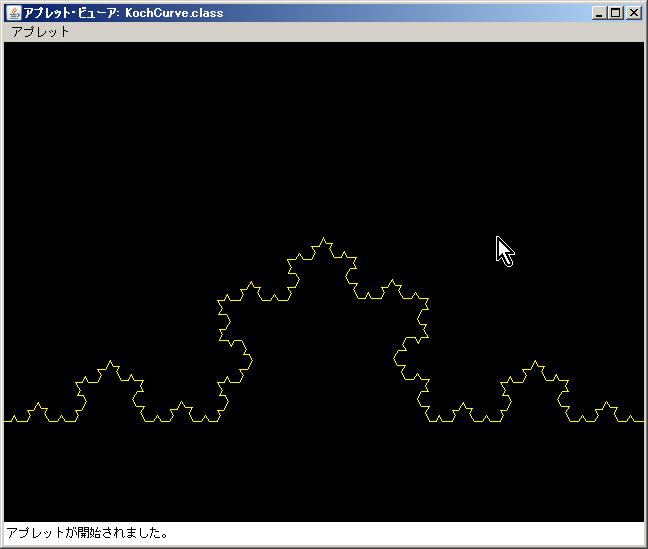
代表的なもので私も好きなものに「コッホ曲線」がありますね。
雪の結晶のような図形です。
■コッホ曲線 - Wikipedia
http://ja.wikipedia.org/wiki/%E3%82%B3%E3%83%83%E3%83%9B%E6%9B%B2%E7%B7%9A
これは「線の真ん中に山がある」そんな図形の集まりでできています。
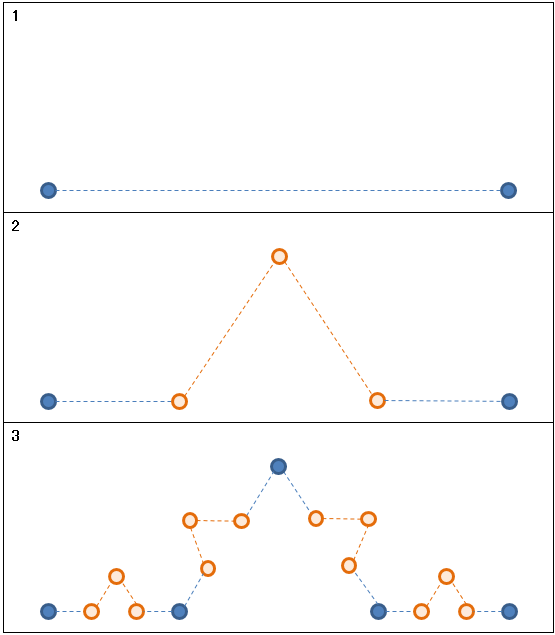
描き方の考え方としては
「線の真ん中に山を作り、そうしてできたそれぞれの線の真ん中にまた山を作り…」
を繰り返す、そういうことになります。
よくよく見ると、山は正三角形になっており、その1辺と左右の辺の長さは等しいことが分かるかと思います。
今回、Javaでコッホ曲線を描くプログラムを作りました。
アプレットとして作ってあります。
興味がありましたら、打ち込んで…いや雑誌じゃないんだからコピペでいいですね。
動かしてみてください。
Eclipseで実行するときは、「Javaアプリケーション」ではなく「Javaアプレット」で実行してください。
import java.applet.Applet;
import java.awt.Color;
import java.awt.Graphics;
public class KochCurve extends Applet {
private static final long serialVersionUID = 1L;
private static final double PAI = 3.141592653589393238462643383279;
private static final double thetaOf60Degree = 60 * PAI / 180;
private int maxLevel = 4;
public void init() {
setSize(640,480);
setBackground(Color.BLACK);
}
public void paint(Graphics g) {
g.setColor(Color.YELLOW);
drawKochCurve(g, 0, 100, 639, 100, 0);
}
private void drawKochCurve(Graphics g, int x1, int y1, int x2, int y2, int level) {
if (level == maxLevel) {
g.drawLine(x1, 479 - y1, x2, 479 - y2);
} else {
int vx = (x2 - x1) / 3;
int vy = (y2 - y1) / 3;
int xx1 = x1 + vx;
int yy1 = y1 + vy;
int[] v1 = rotate(thetaOf60Degree, vx, vy);
int xx2 = xx1 + v1[0];
int yy2 = yy1 + v1[1];
int[] v2 = rotate(-thetaOf60Degree, vx, vy);
int xx3 = xx2 + v2[0];
int yy3 = yy2 + v2[1];
level++;
drawKochCurve(g, x1, y1, xx1, yy1, level);
drawKochCurve(g, xx1, yy1, xx2, yy2, level);
drawKochCurve(g, xx2, yy2, xx3, yy3, level);
drawKochCurve(g, xx3, yy3, x2, y2, level);
}
}
private int[] rotate(double theta, int x, int y) {
double sinTheta = Math.sin(theta);
double cosTheta = Math.cos(theta);
int x2 = (int)(cosTheta * x - sinTheta * y);
int y2 = (int)(sinTheta * x + cosTheta * y);
return new int[] {x2, y2};
}
}
今回は座標を求めるのに三角関数をつかいました。
三角関数は苦手な方は苦手だと思いますが、面白い、あるいは綺麗な図形を
コンピュータに描かせるのに何かと使えます。
かいつまんで座標の計算方法を言うと、次のようになります。
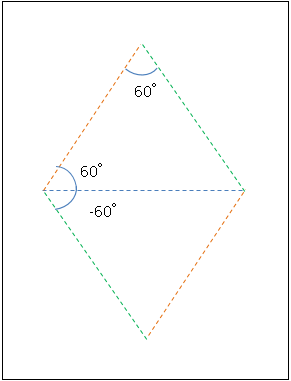
(1) 起点となる座標から、目的点の座標までのベクトルの、三分の一の長さのベクトル(以下A)を求める。
(2) そのベクトルを正方向に60°回転したベクトル(以下B)と、マイナス60°回転したベクトル(以下C)を求める。
(3) 以下のように座標を計算する。
[1] 起点。
[2] 起点からベクトルAだけ移動した位置。
[3] [2]の点からベクトルBだけ移動した位置。
[4] [3]の点からベクトルCだけ移動した位置。
[5] 目標点。
ちなみに、三角関数を使わなくても座標計算をする方法はあります(タブン)。
フラクタル図形の描画処理は、メソッドが自分自身を呼び出す、いわゆる「再帰呼び出し」によって目的を達成します。
フィールドのmaxLevelの値を大きくすると再帰レベルを上げることができ、より細かい図形になります…が、あまりやりすぎると描画がつぶれて微妙なことになります(笑)
ちなみにコッホというのはこの曲線を考案したスウェーデンの数学者、ヘルゲ・フォン・コッホという人です。1870年から1924年に生きた人です。
そのころは今のようなコンピュータはまだないでしょうが、紙に書くこともできますし、概念は完成していたのでしょうね。
ついでなのでもう1つ
もう1つ、私が好きなフラクタル図形である
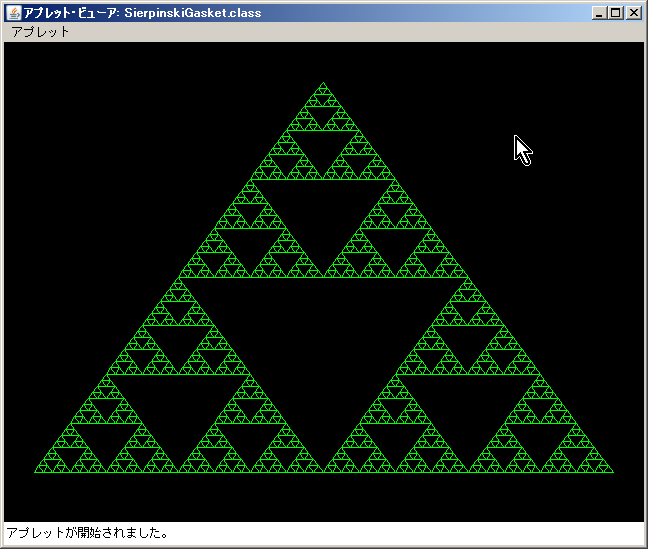
「シェルピンスキーのギャスケット」
これについてもご紹介します。
■シェルピンスキーのギャスケット - Wikipedia
http://ja.wikipedia.org/wiki/%E3%82%B7%E3%82%A7%E3%83%AB%E3%83%94%E3%83%B3%E3%82%B9%E3%82%AD%E3%83%BC%E3%81%AE%E3%82%AE%E3%83%A3%E3%82%B9%E3%82%B1%E3%83%83%E3%83%88
これは、三角形の中に三角形を書いていく図形です。
やり方は、次のようになります。
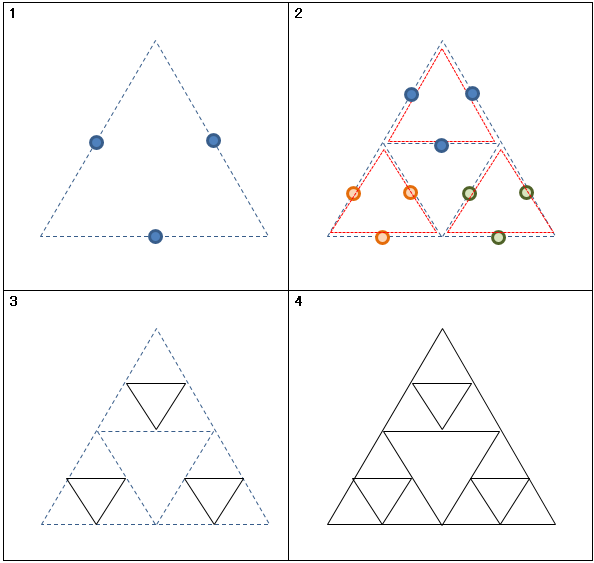
(1) 三角形を描く。
(2) 3辺の中点を求め、それらを頂点に持つ三角形を描く。
(3) そうすると周囲に3つの小さい三角形ができるので、それぞれについて(2)を実施する。
(真ん中の三角形はそのまま。)
※(2)と(3)を繰り返す。
本当は塗りつぶされた三角形をくりぬいて行くというシナリオだった気がしますが、まあそこは気にせず(笑)。
これも、Javaでプログラムを書いてみました。
import java.applet.Applet;
import java.awt.Color;
import java.awt.Graphics;
public class SierpinskiGasket extends Applet{
private static final long serialVersionUID = 1L;
private int maxLevel = 6;
public void init() {
setSize(640,480);
setBackground(Color.BLACK);
}
public void paint(Graphics g) {
g.setColor(Color.GREEN);
drawSierpinskiGasket(g, 319, 40, 30, 430, 609, 430, 0);
}
private void drawSierpinskiGasket(Graphics g, int x1, int y1, int x2, int y2, int x3, int y3, int level) {
if (level == maxLevel) {
g.drawLine(x1, y1, x2, y2);
g.drawLine(x2, y2, x3, y3);
g.drawLine(x3, y3, x1, y1);
} else {
int xx1 = (int)((x1 + x2) / 2.0);
int yy1 = (int)((y1 + y2) / 2.0);
int xx2 = (int)((x2 + x3) / 2.0);
int yy2 = (int)((y2 + y3) / 2.0);
int xx3 = (int)((x3 + x1) / 2.0);
int yy3 = (int)((y3 + y1) / 2.0);
level++;
drawSierpinskiGasket(g, x1, y1, xx1, yy1, xx3, yy3, level);
drawSierpinskiGasket(g, x2, y2, xx1, yy1, xx2, yy2, level);
drawSierpinskiGasket(g, x3, y3, xx3, yy3, xx2, yy2, level);
}
}
}
ちなみに、シェルピンスキーはポーランドの数学者、ヴァツワフ・シェルピンスキという人です。1882年から1969年に生きた人です。
さらに、シェルピンスキーは「シェルピンスキーのカーペット」「シェルピンスキー曲線」というのも考案しています。
まとめ
仕事でコーディングをしていると、
とかく分かりづらい・つまらないコードができあがることもしばしばですが…
こういう綺麗な図形を描かせてみることで、気分転換を図るというのはいかがでしょうか。
きっと「プログラミングは本来楽しいものである」ということを思い出させてくれます^^
それから、フラクタル図形は他にもいっぱい種類があります。
ぜひGoogleで画像検索してみてください!
■フラクタル図形 - Google 検索
https://www.google.co.jp/search?q=%E3%83%95%E3%83%A9%E3%82%AF%E3%82%BF%E3%83%AB%E5%9B%B3%E5%BD%A2&oe=utf-8&hl=ja&um=1&ie=UTF-8&tbm=isch
以上、きうちでした。それではまた!
よいクリスマスを!そしてよいお年を!
…っとその前に忘年会かな(笑)
追記
C#版、載せました!
http://qiita.com/kiuyas/items/4c05cfa5e341e9788b46
2014.12.21 追記
VB.NET版も載せました!
http://qiita.com/kiuyas/items/bf495bd915910aaf5d9c