交線を求める

過去に交点を求める記事を書きましたが、今回は交線を求める記事を書きたいと思います。

Houdiniでフェースとフェースの交線を求める場合は、
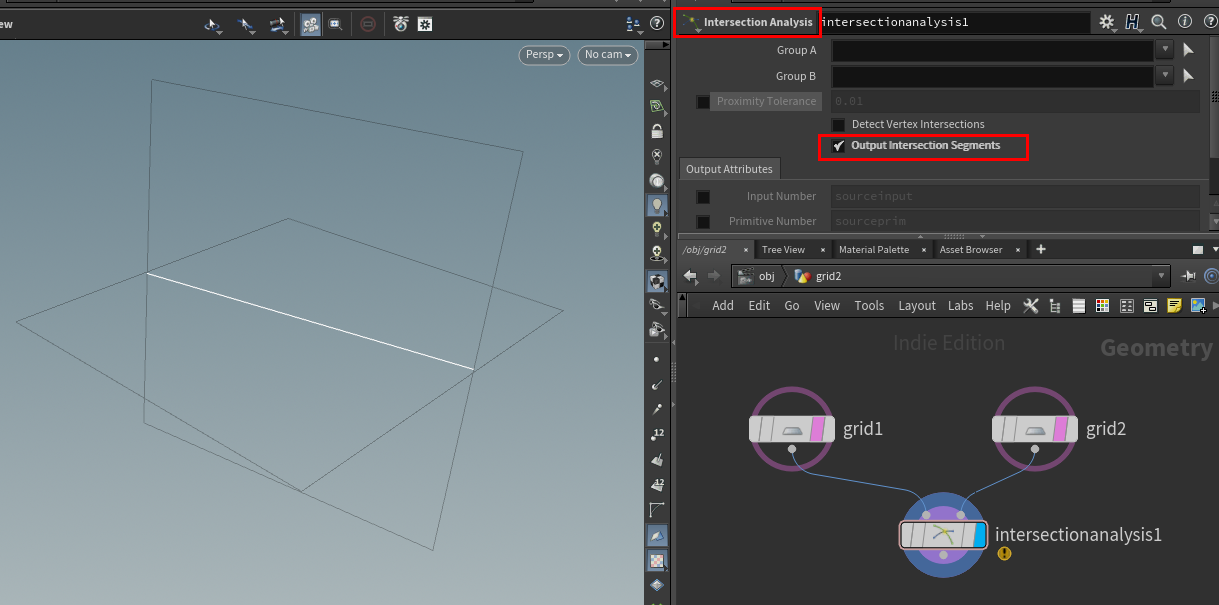
Intersection Analysis SOPを使用して、そのノードのOutput Intersection Segmentsチェックボックスを有効にすることです。

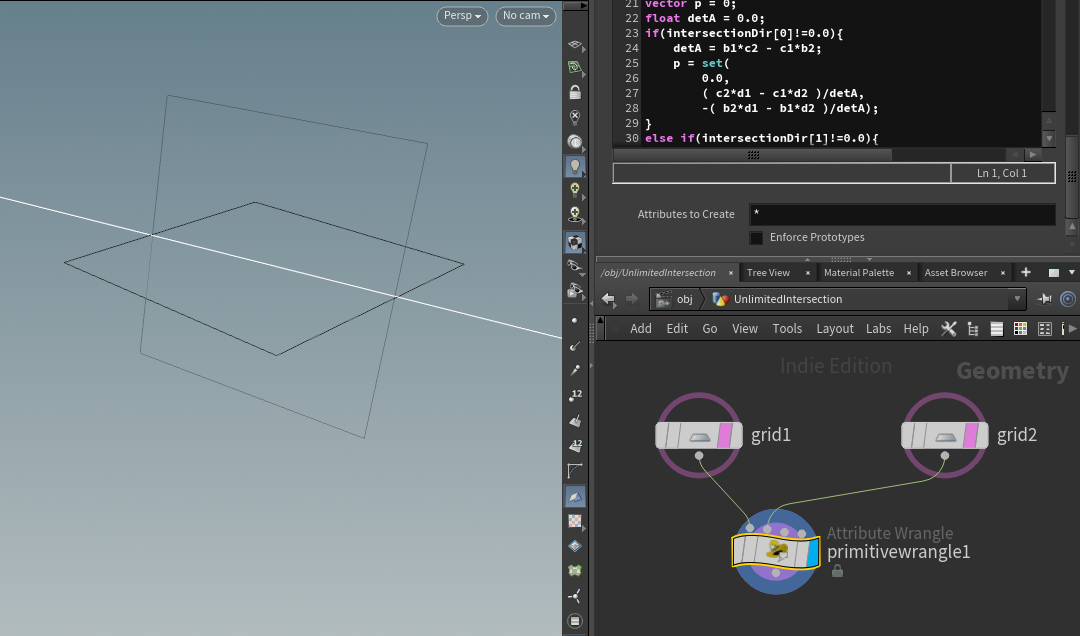
今回は、SOPを使用せずにWrangleで交線を求めたいと思います。
そういえば？VEX関数にintersect関数があるのでそれを使用すれば求まり・・・ません
そのintersect関数は光線(Ray)と面との交差ですね。
Wrangleで面と面の交線を求めるとなると独自に数式を求めてそれをコードにする必要があります。

では、数学的に面と面の交線はどうやって求めれば良いでしょう？
交線の方向はすぐに思いつくことでしょう。

交線の方向L = 面1の法線と面2の法線の両方に直交するベクトル。
つまり、面1の法線と面2の法線の外積で求まりますね。

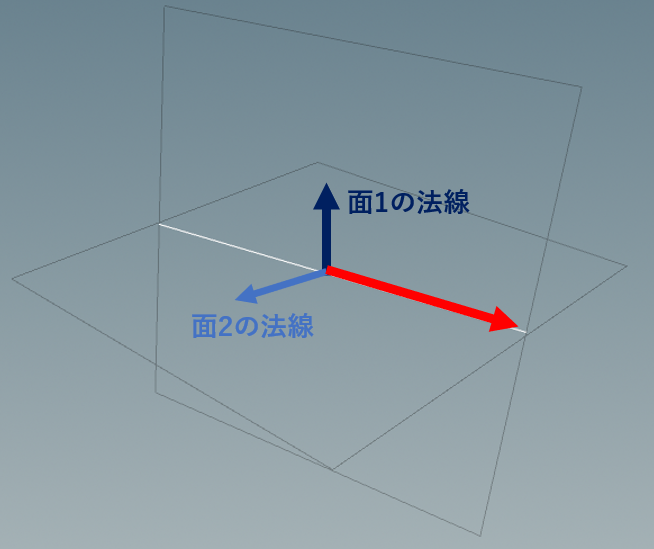
後は、交線が通る任意の1点Pを求めれば
交線 = P + α*L
という式ができますね。

平面1:

a1X+b1Y+c1Z=d1

平面2:

a2X+b2Y+c2Z =d2

とした場合、それぞれの平面を通る任意の1点は、X,Y,Zどれかを0として決め打ちすることで、この連立方程式を解くことができます。
交線方向LのX成分が0でない場合(YZ平面上にない場合)、Xを0と決め打ちすることでY,Zの値が求まります。
同様にLのY成分が0でない場合、Yを0と決め打ちすることでX,Zの値が求まり、
LのZ成分が0でない場合、Zを0と決め打ちすることでX,Yの値が求まります。

これをWrangleで実装すると

PrimitiveWrangle

vector nul = 0;
int success = 0;
vector curPrimNormal = prim_normal(0,0,nul);
vector curPrimPoint = primattrib(0,"P",0,success);
vector targetPrimNormal = prim_normal(1,0,nul);
vector targetPrimPoint = primattrib(1,"P",0,success);
//平面1と平面2の交線方向
vector intersectionDir = normalize(cross(curPrimNormal,targetPrimNormal));

//平面1の式の係数
float a1 = curPrimNormal.x;
float b1 = curPrimNormal.y;
float c1 = curPrimNormal.z;
float d1 = a1*curPrimPoint.x + b1*curPrimPoint.y + c1*curPrimPoint.z;
//平面2の式の係数
float a2 = targetPrimNormal.x;
float b2 = targetPrimNormal.y;
float c2 = targetPrimNormal.z;
float d2 = a2*targetPrimPoint.x + b2*targetPrimPoint.y + c2*targetPrimPoint.z;

vector p = 0;
float detA = 0.0;
if(intersectionDir[0]!=0.0){
    detA = b1*c2 - c1*b2;
    p = set(
        0.0,
        ( c2*d1 - c1*d2 )/detA,
        -( b2*d1 - b1*d2 )/detA);
}
else if(intersectionDir[1]!=0.0){
    detA = c1*a2 - a1*c2;
    p = set(
        -( c2*d1 - c1*d2 )/detA,
        0.0,
        ( a2*d1 - a1*d2 )/detA);
}
else if(intersectionDir[2]!=0.0){
    detA = a1*b2 - b1*a2;
    p = set(
        ( b2*d1 - b1*d2 )/detA,
        -( a2*d1 - a1*d2 )/detA,
        0.0);
}
int newLine = addprim(0, "polyline");
int newPtNum1 = addpoint(0, p-100.0*intersectionDir);
addvertex(0, newLine, newPtNum1);
int newPtNum2 = addpoint(0, p+100.0*intersectionDir);
addvertex(0, newLine, newPtNum2);

これで、交線を求めることができました。
ただ、これは2枚の平面同士の無限交線の求め方で、実際に欲しいのは複数枚の平面同士の有限交線だと思います。
コードは以下のような感じで書きます。

PrimitiveWrangle

int isInside(vector refPos;int listPoints[]){
    int result = 0;
    int success = 0;
    if(len(listPoints)<3) return result;
    
    vector refPnt,pnt1,pnt2;
    int listTargetPoints[]=listPoints;
    push(listTargetPoints,listTargetPoints[0]);

    float originalArea = 0.0;
    refPnt = pointattrib(1,"P",listTargetPoints[0],success);
    for(int i =0;i<len(listTargetPoints)-3;i++){
        pnt1 = pointattrib(1,"P",listTargetPoints[i+1],success);
        pnt2 = pointattrib(1,"P",listTargetPoints[i+2],success);
        originalArea += 0.5*length(cross(pnt1-refPnt,pnt2-refPnt));
    }
    
    float currentArea = 0.0;
    refPnt = refPos;
    for(int i =0;i<len(listTargetPoints)-1;i++){
        pnt1 = pointattrib(1,"P",listTargetPoints[i],success);
        pnt2 = pointattrib(1,"P",listTargetPoints[i+1],success);
        float tmpArea = 0.5*length(cross(pnt1-refPnt,pnt2-refPnt));
        currentArea += tmpArea;
    }
    if( abs(currentArea - originalArea)<1e-6) result = 1;//微小面積対策として、精度厳しくする
    
    return result;
}

void getIntersection(vector A;vector B;vector C;vector D;int result;vector out)
{
    result = 1;
    if(A==B || C==D){
        result = 0;
        return;
    }
    vector n1 = normalize(B-A);
    vector n2 = normalize(D-C);
    if(abs(1.0-abs(dot(n1,n2)))<1e-6){//平行だった場合
        result = 0;
        return;
   }
    vector AC = C - A;
    float d1 = ( dot(n1,AC) - dot(n2,AC)*dot(n1,n2) ) / ( 1.0 - dot(n1,n2)*dot(n1,n2) );
    float d2 = ( -dot(n2,AC) + dot(n1,AC)*dot(n1,n2) ) / ( 1.0 - dot(n1,n2)*dot(n1,n2) );

    if( abs(d1)<1e-6 ) d1 = 0.0f;
    if( abs(d2)<1e-6 ) d2 = 0.0f;
    if(d1<0.0f || d2<0.0f) {
        result = 0;
        return;
    }
    
    if( abs(d1-distance(A,B)) <1e-6  ) d1 = distance(A,B);
    if( abs(d2-distance(C,D)) <1e-6  ) d2 = distance(C,D);
    
    if(d1>distance(A,B) || d2>distance(C,D)){
        result = 0;
        return;
    }
    vector p1 = A + d1*n1;
    if(distance(B,p1)<1e-6){
        result = 0;
        return;
    }
    out = p1;
    return;
}

void createIntersection(vector startPnt;vector endPnt;int targetPrimNum)
{
    int listPoints[] = primpoints(1,targetPrimNum);
    int newPntCount = 0;
    vector listNewPtPos[];
    if(isInside(startPnt,listPoints)==1){
        push(listNewPtPos,startPnt);
        newPntCount+=1;
    }
    if(isInside(endPnt,listPoints)==1){
        push(listNewPtPos,endPnt);
        newPntCount+=1;
    }
    if(newPntCount<2){
        push(listPoints,listPoints[0]);
        for(int i=0;i<len(listPoints)-1;i++){
            int success = 0;
            vector startPos = pointattrib(1,"P",listPoints[i],success);
            vector endPos = pointattrib(1,"P",listPoints[i+1],success);
            vector out;
            getIntersection(startPnt,endPnt,startPos,endPos,success,out);
            if(success==1){
                if(out!=startPnt && out!=endPnt){
                    push(listNewPtPos,out);
                    newPntCount+=1;
                    if(newPntCount==2) break;
                }
            }
        }
    }
    if(len(listNewPtPos)==2){
        int newLine = addprim(0, "polyline");
        
        foreach(vector eachNewPtPos;listNewPtPos){
            int newPtNum = addpoint(0, eachNewPtPos);
            addvertex(0, newLine, newPtNum);
        }
            
        addprimattrib(0,"line",0);
        setprimattrib(0,"line",newLine,1,"set");
    }
}

void getPrimIntersection(int curPrimNum;int targetPrimNum;int check;vector result1;vector result2)
{
    vector nul = 0;
    int success = 0;
    vector outOrigin=0;
    vector outVector=0; 
    vector curPrimNormal = prim_normal(0,curPrimNum,nul);
    vector curPrimPoint = primattrib(0,"P",curPrimNum,success);
    vector targetPrimNormal = prim_normal(1,targetPrimNum,nul);
    vector targetPrimPoint = primattrib(1,"P",targetPrimNum,success);
    vector intersectionDir = normalize(cross(curPrimNormal,targetPrimNormal));

    float a1 = curPrimNormal.x;
    float b1 = curPrimNormal.y;
    float c1 = curPrimNormal.z;
    float d1 = a1*curPrimPoint.x + b1*curPrimPoint.y + c1*curPrimPoint.z;
    float a2 = targetPrimNormal.x;
    float b2 = targetPrimNormal.y;
    float c2 = targetPrimNormal.z;
    float d2 = a2*targetPrimPoint.x + b2*targetPrimPoint.y + c2*targetPrimPoint.z;

    check = 0;
    vector p = 0;
    float detA = 0.0;
    if(intersectionDir[0]!=0.0){
        detA = b1*c2 - c1*b2;
        p = set(
            0.0,
            ( c2*d1 - c1*d2 )/detA,
            -( b2*d1 - b1*d2 )/detA
        );
        check = 1;
    }
    else if(intersectionDir[1]!=0.0){
        detA = c1*a2 - a1*c2;
        p = set(
            -( c2*d1 - c1*d2 )/detA,
            0.0,
            ( a2*d1 - a1*d2 )/detA
        );
        check = 1;
    }
    else if(intersectionDir[2]!=0.0){
        detA = a1*b2 - b1*a2;
        p = set(
            ( b2*d1 - b1*d2 )/detA,
            -( a2*d1 - a1*d2 )/detA,
            0.0
        );
        check = 1;
    }
    else{
        check = 0;
    }
    p = dot( curPrimPoint - p , intersectionDir ) * intersectionDir + p;
    if(check==1){
        outOrigin = p;
        outVector = intersectionDir;
    } 
    else{
        outOrigin = 0;
        outVector = 0;
    }
    if(check==1){
        int listPoints[] = primpoints(0,curPrimNum);
        vector startPnt = outOrigin - 100*outVector;
        vector endPnt = outOrigin + 100*outVector;
        vector results[]=array(startPnt,endPnt);
        int newPntCount = 0;
        push(listPoints,listPoints[0]);
        for(int i=0;i<len(listPoints)-1;i++){
            vector startPos = pointattrib(0,"P",listPoints[i],success);
            vector endPos = pointattrib(0,"P",listPoints[i+1],success);
            vector out;
            getIntersection(startPnt,endPnt,startPos,endPos,success,out);
            if(success==1){
                results[newPntCount]=out;
                newPntCount+=1;
                if(newPntCount==2) break;
            }
        }
        result1 = results[0];
        result2 = results[1];

        if(newPntCount==2) createIntersection(result1,result2,targetPrimNum);
    }
}
float bounds[]=primintrinsic(0,"bounds",@primnum);
int nearPrims[] = primfind(1,set(bounds[0],bounds[2],bounds[4]),set(bounds[1],bounds[3],bounds[5]));
foreach(int nearPrim;nearPrims){
    int check;
    vector pnt1;
    vector pnt2;
    getPrimIntersection(@primnum,nearPrim,check,pnt1,pnt2);
}

長っっっっっっ！
これでコードによってオブジェクト同士の交線を求めることができました。

まぁ、HIPファイルを添付するので見たい方はどうぞ。こちらです。