交点を求める

はじめに

今回はHoudiniを使って高校数学の勉強をしたいと思います。

よく交点を求めたいってことありませんか？
スクランブル交差点とか歩いてると、交点はどこかなとか。
人混みの中、みんなが見ている視線の交点には一体なにがあるんだろうとか。
ふと、そう考えることもあるでしょう(ねぇよっ！)

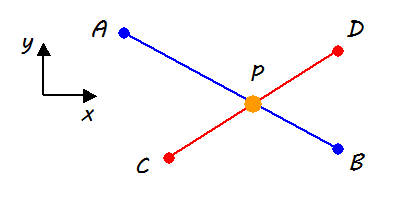
では、問題です。

平面上で直線AB、直線CDの交点pを求めろ

問題の解き方がわかりましたか？
普段Houdiniに限らず3DCGを使っていると線を分割するってことをよくすると思いますが、そもそもどうやって計算してるのでしょう？
おそらく頭の中に浮かぶのは、それらの直線の式の連立方程式を解くっていうのが中学校でやったと思うんですね。

\begin{eqnarray}
  \left\{
    \begin{array}{l}
      y = 3x + 2 \\
      y = -3x + 5
    \end{array}
  \right.
\end{eqnarray}

でも、CG触ってると、任意の2直線の交点を求める必要性に駆られるときがよくありますが、中学校でやってたような上記のような式から連立方程式を解くって・・
やらないです
しかも、それ2次元だし。ax+by+cz=0でやっても、"節子、それ線やない(a,b,c)を法線とする平面や"って言われるし。

じゃ、どうやって交点を解くのでしょう？

Curvesect SOP、Intersection Analysis SOP、intersect VEX関数を使えば交点が求められます。

終わり。
 
 
 
 
いやいやいや、そのために書いたんじゃない。
例えば、

• 線と線が厳密に交差していない、いわば、ねじれの状態でも交点を計算したい
• 線と線の延長線上の交点を計算したい
• 線と線が平行だった時の処理を加えたい

このような交点計算を独自にカスタマイズしたいのです。
中学校でやった2次元のあらかじめ与えられた連立方程式から交点を求める方法ではなく、プログラムに実装できる形で交点を求めるにはどうすればいいでしょうか？

それは、内積を使えば求めることができます。
もうわかってる人は、この記事はスキップでいいと思います。

やっぱ内積は必須

では、内積なにそれおいしいの？っていう人のために2年前のアドカレの記事をどうぞ。
https://qiita.com/kit2cuz/items/ba67b8dee3fd5d0de479#%E5%86%85%E7%A9%8D%E3%81%AB%E3%81%A4%E3%81%84%E3%81%A6

内積を使えば、点から直線までの最短距離を求めることができます。
それを応用すれば交点だって求まります。

では、ピンと来ない人は下図を想像すればいいんです。

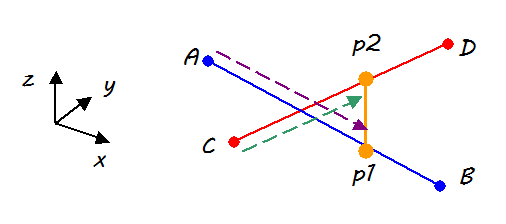
ベクトルABがベクトルp1p2と直交している、つまり、それらのベクトルの内積は0
ベクトルCDがベクトルp1p2と直交している、つまり、それらのベクトルの内積は0

はい、内積を使ったベクトル数学と連立方程式の組み合わせを使います。

この条件を満たす計算式を考えれば、交点が求まりますよね。
Aとp1までの距離をd1、Cとp2までの距離をd2、ベクトルABの長さ1のベクトルをn1、ベクトルCDの長さ1のベクトルをn2とすれば、
ベクトルAp1 = d1*n1
ベクトルCp2 = d2*n2
と表現することができます。
ベクトルAB・ベクトルp1p2 = 0
ベクトルCD・ベクトルp1p2 = 0
p1=A+d1*n1、p2=C+d2*n2なのでそれを代入し、ベクトルABをAB、ベクトルCDをCD、ベクトルACをACと表記すると、
AB・(AC+d2*n2-d1*n1)=0
CD・(AC+d2*n2-d1*n1)=0
これらの連立方程式を解きやすくする鍵はABもCDも正規化したn1,n2に置き換えることです。
p1とp2がAとCだけを考慮しているので、BとDの情報は不要、むしろ複雑化してしまうので
n1・(AC+d2*n2-d1*n1)=0
n2・(AC+d2*n2-d1*n1)=0
と変換します。
ここからd1とd2さえ求まればよく、この2つの連立方程式を見ると、d1=ほにゃらら、d2=ほにゃららという形式に落とし込むことができそうです。つまり、問題が解ける！
n1・AC + d2*(n1・n2) - d1*(n1・n1) = 0
n2・AC + d2*(n2・n2) - d1*(n1・n2) = 0
同じベクトル同士の内積は、そのベクトルの長さの2乗です。
単位ベクトルの長さは1なので、n1・n1、n2・n2は1になります。
つまり、
n1・AC + d2*(n1・n2) - d1 = 0
n2・AC + d2 - d1*(n1・n2) = 0
ということは、
d1 = n1・AC + d2*(n1・n2)
d2 = d1*(n1・n2) - n2・AC
つまり、
d1 = n1・AC + d1*(n1・n2)(n1・n2) - (n2・AC)(n1・n2)
= ( n1・AC - (n2・AC)(n1・n2) ) / ( 1 - (n1・n2)(n1・n2) )
d2 = (n1・AC)(n1・n2) + d2(n1・n2)(n1・n2) - n2・AC
= ( -n2・AC + (n1・AC)(n1・n2) ) / ( 1 - (n1・n2)*(n1・n2) )

d1,d2が求まれば、p1=A+d1*n1、p2=C+d2*n2が求まるので、これで交点が算出できます。
これをWrangleで実装してみます

カスタマイズしたい交点計算の仕様は以下の内容を想定します。

• 1本以上の直線(AB)と1本以上のポリラインの交点を求める
• ポイントAからポイントBに向かった延長線上の交点を加味する。複数の交点が存在すれば、Bに近い交点を取得する
• 交点がなければポイントBにする
• 直線とポリラインが厳密に交差していない(ねじれの関係)場合は、ポリライン上の交点を取得する

PrimitiveWrangle

//交点を取得するサブルーチン
vector getIntersection(vector A;vector B;vector C;vector D)
{
   if(A==B || C==D) return B;//同一点ならBを返す
   vector n1 = normalize(B-A);
   vector n2 = normalize(D-C);

   //2直線が平行な場合の挙動を定義する
   if(abs(1.0-abs(dot(n1,n2)))<1e-5) return B;

   vector AC = C - A;
   float d1 = ( dot(n1,AC) - dot(n2,AC)*dot(n1,n2) ) / ( 1 - dot(n1,n2)*dot(n1,n2) );
   float d2 = ( -dot(n2,AC) + dot(n1,AC)*dot(n1,n2) ) / ( 1 - dot(n1,n2)*dot(n1,n2) );

   //交点がCD上にない場合の挙動を定義する
   if(d1<0 || d2<0) return B;//d1またはd2がマイナス値ならポイントBを返す
   else if(d2>distance(C,D)) return B;//d2がCDより長ければポイントBを返す

   //好きなようにp1,p2からどのような形で交点を算出するか定義する
   vector p1,p2;
   p1 = A + d1*n1;
   p2 = C + d2*n2;
   return p2;
}
//メイン処理
int listPoints1[] = primpoints(0, @primnum);
vector A = point(0,"P",listPoints1[0]);
vector B = point(0,"P",listPoints1[1]);
vector p=B;
float minimumDist = 1e+6;
for(int i=0;i<nprimitives(1);i++){//nprimitives(1)は2番目の入力のプリミティブの数を返します
    int listLinearVertices[] = primvertices(1, i);//2番目の入力の各プリミティブの線形頂点番号のリストを取得する
    for(int curIndex=0;curIndex<len(listLinearVertices);curIndex++){
        int curPrimOnC = vertexprim(1,listLinearVertices[curIndex]);//現行線形頂点番号が属するプリミティブ番号を取得する
        int nextIndex = curIndex+1;
        int curPrimOnD = vertexprim(1,listLinearVertices[nextIndex]);//次の線形頂点番号が属するプリミティブ番号を取得する
        if(curPrimOnC!=curPrimOnD){//現行線形頂点と次の線形頂点が別のプリミティブに属する場合は、そのポイント間で交点を計算したくないのでスキップする
            continue;
        }
        vector C = point(1,"P",vertexpoint(1,listLinearVertices[curIndex]));//Cのポイント座標を取得する
        vector D = point(1,"P",vertexpoint(1,listLinearVertices[nextIndex]));//Dのポイント座標を取得する
        vector outP = getIntersection(A,B,C,D);//交点を計算
        if(outP!=B && distance(B,outP)<minimumDist){//計算した交点とBの距離が他の交点よりも近ければ、その交点を採用する
            p = outP;
            minimumDist = distance(B,outP);
         }
    }
}
removeprim(0, @primnum, 1);//プリミティブを削除する
addpoint(0,p);//交点を追加する

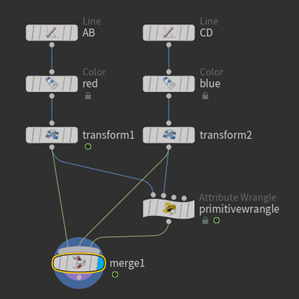
このようにLine SOPを2つ用意し、Primitive Wrangle SOPの1番目、2番目の入力にそれぞれ直線を接続します。
すると、下図のように2直線が完全に交差していなくても交点を求めることができます。

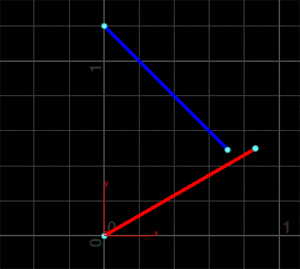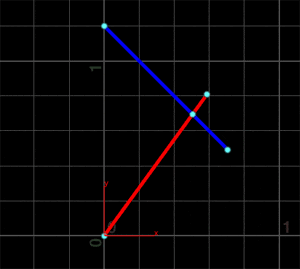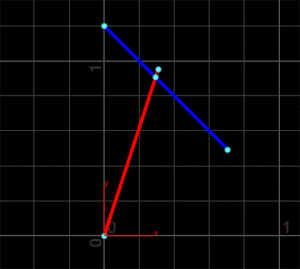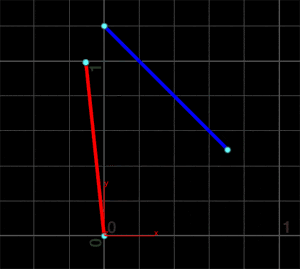
Primitive Wrangle SOPの2番目の入力にポリラインを接続すると、こんな感じになります。

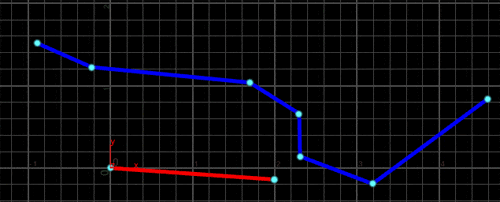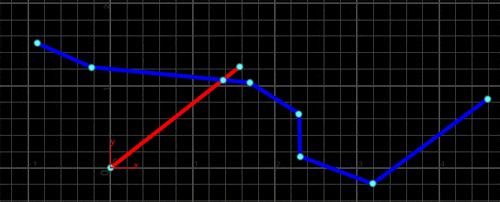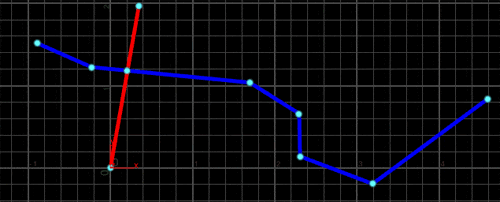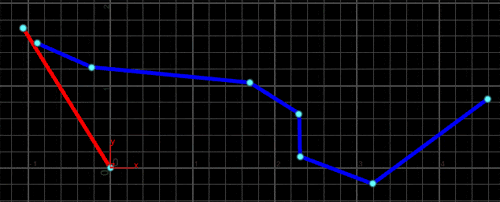
これで、好きなように交点を計算することができました。
めでたしめでたし

 
 
 
 
 
 
 
 
 
 
 
 
 
 
で終わらないよねぇ。
ここまでで何か疑問に思わないと駄目でしょ。
「え？こんなことMELでもできるよ。」
「移植性考えたらMayaとHoudiniでも使えるようにPython SOPでやった方がいいだろうし、Wrangleでやるメリットってあるの？」
「パフォーマンスモニタで調べてみるとIntersection Analysis SOPの方が高速じゃねぇかごらぁ。」
「つーか、上記のコードなんてVEXの並列処理のメリットがまったくいかされてないじゃん。」
「直線とポリラインの交点を求める時には、ポリラインの方をRun Overさせた方が処理効率がよくないか？」
と思われた方がいたら、あなたはHoudinistだ！おら嬉しいぞ。ワックワクすんぞ

1本の直線と1本のポリラインの交点を求めるコードを書く時は、そのポリラインの各エッジに対してRun Overさせたほうが並列処理できますよね。
ポリラインは1本のプリミティブなので、Wrangle SOPのRun OverをPrimitiveに設定しても並列にならずforループを使わざるを得ません。
上記のコードは、複数交点のうち、Bに近いポイントだけを求めたかったのでPrimitive Wrangle SOPを使いました。
もし、1本の直線とポリラインから 複数の交点 を求める場合には、もっと効率のよいコードを書くことができます。
エッジに対してRun Overさせることはできないのですが、これは頂点で代用できます。

• Wrangle SOPの1番目の入力にポリライン、2番目の入力に直線(AB)を指定する
• ポイントAからポイントBに向かった延長線上の交点を加味する。複数の交点も取得する
• 直線とポリラインが厳密に交差していない(ねじれの関係)場合は、ポリライン上の交点を取得する

以下がVertex Wrangleのコードです。

VertexWrangle

//交点を取得するサブルーチン
vector getIntersection(vector A;vector B;vector C;vector D;int test)
{
   if(A==B || C==D) return B;//同一点ならBを返す
   vector n1 = normalize(B-A);
   vector n2 = normalize(D-C);

   //2直線が平行な場合の挙動を定義する
   if(abs(1.0-abs(dot(n1,n2)))<1e-5){
       test = 0;
       return B;
   }

   vector AC = C - A;
   float d1 = ( dot(n1,AC) - dot(n2,AC)*dot(n1,n2) ) / ( 1 - dot(n1,n2)*dot(n1,n2) );
   float d2 = ( -dot(n2,AC) + dot(n1,AC)*dot(n1,n2) ) / ( 1 - dot(n1,n2)*dot(n1,n2) );

   //交点がCD上にない場合の挙動を定義する
   if(d1<0 || d2<0){test=0;return B;}//d1またはd2がマイナス値ならポイントBを返す
   else if(d2>distance(C,D)){test=0;return B;}//d2がCDより長ければポイントBを返す

   //好きなようにp1,p2からどのような形で交点を算出するか定義する
   vector p1,p2;
   p1 = A + d1*n1;
   p2 = C + d2*n2;
   test = 1;
   return p2;
}
//メイン処理
int listPoints1[] = primpoints(1, 0);
vector A = point(1,"P",listPoints1[0]);
vector B = point(1,"P",listPoints1[1]);
int curPrimOnC= vertexprim(0,@vtxnum);
int curPrimOnD= vertexprim(0,@vtxnum+1);
if(curPrimOnC!=curPrimOnD){
    removepoint(0,vertexpoint(0,@vtxnum));
    return;
}
vector C = point(0,"P",vertexpoint(0,@vtxnum));
vector D = point(0,"P",vertexpoint(0,@vtxnum+1));
vector p=C;
int test = 0;
p = getIntersection(A,B,C,D,test);
removepoint(0,vertexpoint(0,@vtxnum));
if(test==1){
    addpoint(1,p);
}

まとめ

• 内積は便利だよ
• 作成した数式をサブルーチンで定義する方法を教えたよ
• VEXはそこらのスクリプトと違って並列処理が簡単に実装できることを説明したよ
• エッジの処理は頂点で代用できるよ

おしまい