はじめに
私はゲーム会社でデータ分析を行っています。
アートの方々がアイテムの装着率を気にしているのを見る度に、「リリース前にクリエイティブを定量的に評価できる指標が無いだろうか?」と、考えていました。
ディープラーニングを勉強してみて「これならもしかしてできるんじゃないか??」と思い、VGGから初めて、いくつかのアルゴリズムを試してきました。
まだしっかりした結果が出ていないものですが、公開しようと思います1。
データは、業務外の私的な研究なので、ネット上から収集できるデータにしました。
今回はゆるキャラグランプリ2017にエントリーしたキャラクターの画像から、そのキャラクターの最終的な順位を予想してみます。
結論
- 学習データでの精度は98%、バリデーションデータに対しての精度は88%、テストデータに対しての精度は23%でした。
- 新規エントリーと過去エントリー実績があるキャラクターに分けてテストデータでの予想精度を分析してみると、新規エントリーしたキャラクターの順位はまったく予想できておらず、過去にエントリーしたことのあるキャラクターに対しての予想精度も悪いという結果が得られました。
- 学習データの順位帯には2011~2016年までの順位帯の中で最も多く属した順位帯を採用したため、時系列情報が落ちてしまい、2017年の予想精度が悪くなりました。
- 後で見るように、過去エントリーしたことがあるキャラクターの順位の変動にはトレンドが存在しているため、RNN等の時系列を考慮したモデルを使う必要がありました。
- いわゆるコールドスタート問題で初参加のキャラクターの予想が悪いです。
モデルの仮定
今回のモデル構築では以下を仮定しています。
- 人はかっこいいや可愛いなど見た目で投票する
- トレンドの変化は無い2
使用したデータとディープラーニングアルゴリズム
-
トレーニングデータ
ゆるキャラグランプリの2011年 ~ 2016年の総合ランキングの順位とキャラクターの画像
総合ランキングは期間中に最も多く属した順位帯を採用しました。
属した回数にタイが発生した場合は最も小さい順位帯を採用しています。 -
予想するデータ
ゆるキャラグランプリの2017年の総合ランキングの順位
※ランキングがご当地と企業・その他で分かれているので、データを取得後に得票数から総合ランキングを作成しました。 -
適用したアルゴリズム
Inception-V3
今回はkerasで提供されているAPIをそのまま適用しました。
モデルの詳細はhttps://keras.io/ja/applications/#inceptionv3をご確認下さい。
トレーニングスクリプト
トレーニングで使ったスクリプトは次の3つから構成されています。
-
model.pykerasのモデルを構築します。 -
utils.pyデータのロードやトレーニングデータをシャッフルする関数が定義されています。 -
trainer.pyモデルのトレーニングを実行します。
# -*- coding: utf-8 -*-
from keras.applications.inception_v3 import InceptionV3
def build_model():
return InceptionV3(include_top=True, weights=None, classes=10)
if __name__ == '__main__':
model = build_model()
model.summary()
# -*- coding: utf-8 -*-
import csv
import os
from keras.utils import to_categorical
import numpy as np
from skimage.io import imread
def _load_yuruchara_data(csv_path, image_dir):
points = []
images = []
with open(csv_path, 'r') as f:
reader = csv.DictReader(f)
for row in reader:
pt = int(row['point'])
points.append([pt])
fn = row['filename']
img = imread(os.path.join(image_dir, fn))
images.append(img)
points_array = np.array(points)
images_array = np.array(images)
return images_array, points_array
def _load_yuruchara_decile_data(csv_path, image_dir):
deciles = []
images = []
with open(csv_path, 'r') as f:
reader = csv.DictReader(f)
for row in reader:
d = int(row['ranking_class'])
# To use `to_categorical`, we must calculate d - 1.
deciles.append(d-1)
fn = row['filename']
img = imread(os.path.join(image_dir, fn))
images.append(img)
deciles_array = to_categorical(deciles)
images_array = np.array(images)
return images_array, deciles_array
def load_yuruchara_data():
TRAIN_DIR = '/home/ishiyama/yuruchara/data/train'
train = _load_yuruchara_data(
csv_path=os.path.join(TRAIN_DIR, 'yuruchara_train_data.csv'),
image_dir=os.path.join(TRAIN_DIR, 'image'))
TEST_DIR = '/home/ishiyama/yuruchara/data/test'
test = _load_yuruchara_data(
csv_path=os.path.join(TEST_DIR, 'yuruchara_test_data.csv'),
image_dir=os.path.join(TEST_DIR, 'image'))
return train, test
def load_yuruchara_decile_data():
TRAIN_DIR = '/home/ishiyama/yuruchara/decile_data/train'
train = _load_yuruchara_decile_data(
csv_path=os.path.join(TRAIN_DIR, 'train_data.csv'),
image_dir=os.path.join(TRAIN_DIR, 'image', '299'))
TEST_DIR = '/home/ishiyama/yuruchara/decile_data/test'
test = _load_yuruchara_decile_data(
csv_path=os.path.join(TEST_DIR, 'test_data.csv'),
image_dir=os.path.join(TEST_DIR, 'image', '299'))
return train, test
def shuffle_data(x, y):
x_length = x.shape[0]
y_length = y.shape[0]
if x_length != y_length:
raise ValueError('lengths of x and y must be same length.')
index = np.arange(x_length)
np.random.shuffle(index)
return x[index, :, :, :], y[index, :]
def normalize_images(images):
shape = images.shape
normalized = np.zeros(shape)
channels = shape[-1]
for ch in range(channels):
layers = images[:, :, :, ch]
mean = layers.mean()
scale = layers.max()
normalized[:, :, :, ch] = (layers - mean) / scale
return normalized
if __name__ == '__main__':
train, test = load_yuruchara_decile_data()
train_x, train_y = shuffle_data(x=train[0], y=train[1])
print(train_x.shape)
print(train_y.shape)
# -*- coding: utf-8 -*-
""" Predicting votes on Yuruchara GP with Inception V3. """
import sys
import keras
from utils import load_yuruchara_decile_data, shuffle_data
from model import build_model
EPOCHS = 50
LOG_DIR = './logs'
model = build_model()
model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
callbacks = keras.callbacks.TensorBoard(log_dir=LOG_DIR)
(train_x, train_y), (test_x, test_y) = load_yuruchara_decile_data()
train_x, train_y = shuffle_data(train_x, train_y)
model.fit(x=train_x,
y=train_y,
epochs=EPOCHS,
validation_split=0.1,
verbose=2,
callbacks=[callbacks])
model.evaluate(x=test_x, y=test_y)
model.save('yuruchara_inception01.h5')
実行結果
トレーニングデータでは精度が98%まで上昇したが、バリデーションでは88.1%にとどまりました。
2017年のデータで行った予想のテストでは、正解率は22.77%程度しかありません。
この結果は今回のモデルが大きな問題を持っていることを示しています。
実は2017年にゆるキャラグランプリにエントリーした1,098体のキャラクターのうち、845体(約77%)が過去にエントリーした経験があります。
そのため、本来ならば、テスト用に残しておいた2017年の画像の3/4がトレーニングデータに含まれていることになるので、トレーニングデータにオーバーフィッテングしていることから考えると、テストの精度もそれなりに高くなるはずですが、実際にはそうなっていません。
-
テストデータでの精度が悪かったことに対する仮説
原因として挙げられるのは、このモデルでは時系列を考慮していないことです。
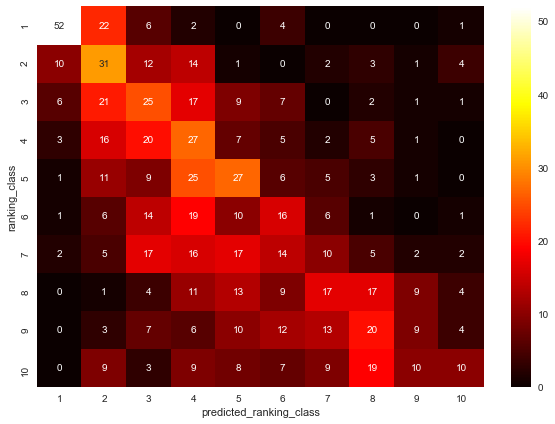
実際、下で作成した予想の順位帯と実際の順位帯のヒートマップを見ると、予想が外れた場合の実際の順位は左上から右下への対角線より下側になっているケースが多いです。
したがって、2017年の順位は2011~2016年までの実績よりも下がる傾向があると考えられます。
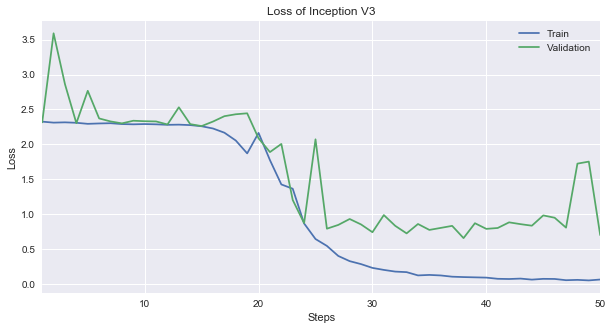
損失関数の推移
損失関数を見てみます。
ここではTensorBoardからトレーニングの損失関数の値run_004-tag-loss.csvとバリデーションの損失関数の値run_004-tag-val_loss.csvをダウンロードしてグラフを作成します。
まずは最後の5エポックの数値を見てみますと、トレーニングデータは0.06まで下がりましたが、バリデーションでは0.7までしか下がりませんでしたので、オーバーフィッテングが疑われます。
import pandas as pd
USECOLS = ['Step', 'Value']
loss_train = pd.read_csv('run_004-tag-loss.csv', usecols=USECOLS)
loss_train.rename(columns={'Value': 'Train'}, inplace=True)
loss_train.Step += 1
loss_train.set_index('Step', inplace=True)
loss_validation = pd.read_csv('run_004-tag-val_loss.csv', usecols=USECOLS)
loss_validation.rename(columns={'Value': 'Validation'}, inplace=True)
loss_validation.Step += 1
loss_validation.set_index('Step', inplace=True)
loss = pd.concat(objs=[loss_train, loss_validation], axis=1)
loss.tail()
| Train | Validation | |
|---|---|---|
| Step | ||
| 46 | 0.072949 | 0.949500 |
| 47 | 0.055133 | 0.807800 |
| 48 | 0.059830 | 1.724219 |
| 49 | 0.052230 | 1.753363 |
| 50 | 0.064824 | 0.700812 |
グラフを書いてみると以下の通りです。
%matplotlib inline
from matplotlib import pyplot as plt
import seaborn as sns
plt.rcParams['figure.figsize'] = (10, 5)
ax = loss.plot(title='Loss of Inception V3')
ax.set_xlabel('Steps')
ax.set_ylabel('Loss')
バリデーションの損失関数は25ステップ以降は下がりませんでした。
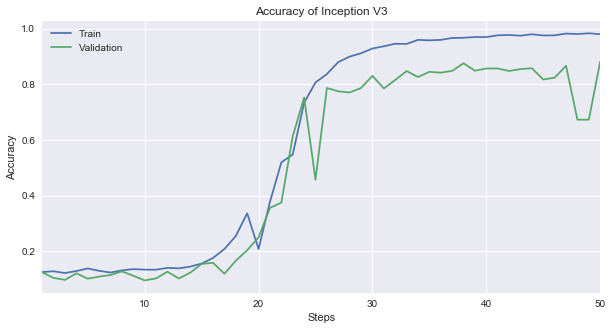
精度の推移
次に精度の推移を見てみます。
損失関数ではバリデーションデータがトレーニングデータのように下がらなかったので、精度の場合もバリデーションがトレーニングに劣っています。
同じように最後の5ステップの精度を見てみますと、トレーニングデータ(Train)で98.8%になっていますが、バリデーションデータ(Validation)は84.7%になっているのが分かります。
USECOLS = ['Step', 'Value']
acc_train = pd.read_csv('run_004-tag-acc.csv', usecols=USECOLS)
acc_train.rename(columns={'Value': 'Train'}, inplace=True)
acc_train.Step += 1
acc_train.set_index('Step', inplace=True)
acc_validation = pd.read_csv('run_004-tag-val_acc.csv', usecols=USECOLS)
acc_validation.rename(columns={'Value': 'Validation'}, inplace=True)
acc_validation.Step += 1
acc_validation.set_index('Step', inplace=True)
acc = pd.concat(objs=[acc_train, acc_validation], axis=1)
acc.tail()
| Train | Validation | |
|---|---|---|
| Step | ||
| 46 | 0.975506 | 0.823511 |
| 47 | 0.981715 | 0.865869 |
| 48 | 0.980248 | 0.672498 |
| 49 | 0.982738 | 0.672498 |
| 50 | 0.979668 | 0.880909 |
これをグラフにすると以下のようになります。
%matplotlib inline
from matplotlib import pyplot as plt
import seaborn as sns
plt.rcParams['figure.figsize'] = (10, 5)
ax = acc.plot(title='Accuracy of Inception V3')
ax.set_xlabel('Steps')
ax.set_ylabel('Accuracy')
損失関数の場合と同じようにバリデーションの精度は途中から上がらなくなっています。
予想した順位は以下のようなデータになっています。
predict_result = pd.read_csv('predict_result_20180427112651.csv')
print(predict_result.shape)
predict_result.head(10)
(1098, 7)
| character_id | character_name | prefecture | is_previous | ranking_class | filename | predicted_ranking_class | |
|---|---|---|---|---|---|---|---|
| 0 | 43 | うなりくん | 千葉県 | 1 | 1 | 00000031.jpg | 1 |
| 1 | 166 | ちりゅっぴ | 愛知県 | 1 | 1 | 00002537.jpg | 1 |
| 2 | 619 | トライくん | 大阪府 | 1 | 1 | 00000895.jpg | 2 |
| 3 | 7 | こにゅうどうくん | 三重県 | 1 | 1 | 00000390.jpg | 1 |
| 4 | 326 | 稲敷いなのすけ | 茨城県 | 1 | 1 | 00002736.jpg | 1 |
| 5 | 821 | ジャー坊 | 福岡県 | 0 | 1 | 00003613.jpg | 4 |
| 6 | 23 | カミスココくん | 茨城県 | 1 | 1 | 00002620.jpg | 1 |
| 7 | 24 | 福井市宣伝隊長「朝倉ゆめまる」 | 福井県 | 1 | 1 | 00000877.jpg | 1 |
| 8 | 100 | 滝ノ道ゆずる | 大阪府 | 1 | 1 | 00000009.jpg | 1 |
| 9 | 39 | なーしくん | 愛媛県 | 1 | 1 | 00001988.jpg | 1 |
予想の精度
予測した順位帯が実際の順位帯と同じである割合を調べてみます。
real_ranking_class = predict_result.ranking_class.tolist()
predicted_ranking_class = predict_result.predicted_ranking_class.tolist()
correct_count = 0
for p, r in zip(predicted_ranking_class, real_ranking_class):
correct_count += 1 if p == r else 0
accuracy = correct_count / float(len(predicted_ranking_class))
print('Accuracy: {:0.2f}%'.format(accuracy * 100))
Accuracy: 22.77%
結果は22.77%と低い結果になっていました。
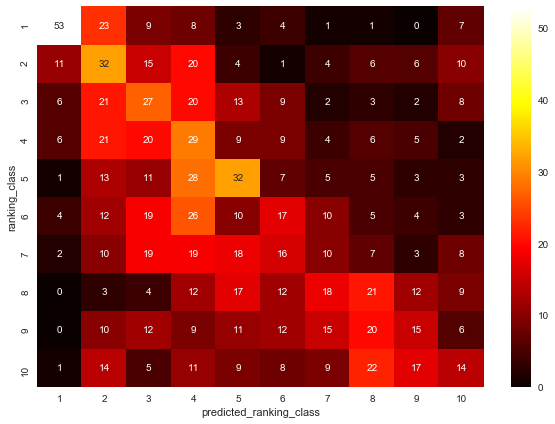
予想した順位帯と実際の順位帯の間に相関があるかを調べる
今回のモデルが何かしらの関係性を学習できているなら、予想した順位と実際の順位の間に相関が生まれるはずです。
横軸に予想した順位帯(predicted_ranking_class)、縦軸に実際の順位帯(ranking_class)を取ってヒートマップ3を作成して検証してみます。
%matplotlib inline
from matplotlib import pyplot as plt
import seaborn as sns
plt.rcParams['figure.figsize'] = (10, 7)
data = pd.pivot_table(
data=predict_result,
index=['ranking_class'],
columns=['predicted_ranking_class'],
values='character_id',
aggfunc='count',
fill_value=0)
sns.heatmap(data, annot=True, cmap='hot')
ヒートマップからは正の相関があると言えます。
しかし、右上よりも左下にデータが集まっていることが気になります。
これは実際の順位が2011年から2016年のデータをもとに予想した順位よりも低い場合に起こるパターンだからです。
正の相関を作っているデータが何なのかを調査する
予想した順位帯と実際の順位帯の間には正の相関があるが、その程度は弱いものでした。
今後モデルを調整するにあたって、どのデータに対してモデルがフィットしていないのかを追求しておく必要があります。
仮説として考えられることは、「2017年に初参加したキャラクターの順位帯が全く予想できていない」ということです。
そのため、予想結果のデータを「過去にエントリーしたキャラクター」と「初参加したキャラクター」の2つに分けて、同じようにヒートマップを作成してみます。
初参加の場合
まずは初参加したキャラクターの予想データを抽出します。
is_newcomer = (predict_result.is_previous == 0)
predict_result_newcomer = predict_result.loc[is_newcomer, :]
print(predict_result_newcomer.shape)
predict_result_newcomer.head(10)
(253, 7)
| character_id | character_name | prefecture | is_previous | ranking_class | filename | predicted_ranking_class | |
|---|---|---|---|---|---|---|---|
| 5 | 821 | ジャー坊 | 福岡県 | 0 | 1 | 00003613.jpg | 4 |
| 12 | 692 | センドくん | 福岡県 | 0 | 1 | 00003573.jpg | 10 |
| 30 | 800 | めいじろう | 東京都 | 0 | 1 | 00003608.jpg | 3 |
| 48 | 78 | さかろん | 埼玉県 | 0 | 1 | 00003454.jpg | 10 |
| 56 | 947 | みえきたん | 三重県 | 0 | 2 | 00003655.jpg | 4 |
| 62 | 1148 | いせわんこ | 三重県 | 0 | 2 | 00003722.jpg | 8 |
| 75 | 843 | ぽぽたん | 埼玉県 | 0 | 2 | 00003620.jpg | 10 |
| 78 | 657 | ブルベリッ娘とブルピヨ | 宮城県 | 0 | 2 | 00003564.jpg | 10 |
| 82 | 736 | なっちゃん | 埼玉県 | 0 | 2 | 00003588.jpg | 5 |
| 83 | 992 | み~ちゅ | 三重県 | 0 | 2 | 00003667.jpg | 9 |
このデータから先程のヒートマップを作成してみます。
contingency_newcomer = pd.pivot_table(
data=predict_result_newcomer,
index=['ranking_class'],
columns=['predicted_ranking_class'],
values='character_id',
aggfunc='count',
fill_value=0)
sns.heatmap(contingency_newcomer, annot=True, cmap='hot')
予想した順位帯と実際の順位帯に正の相関は無いので、初参加のキャラクターの予想はできていないことになります...orz
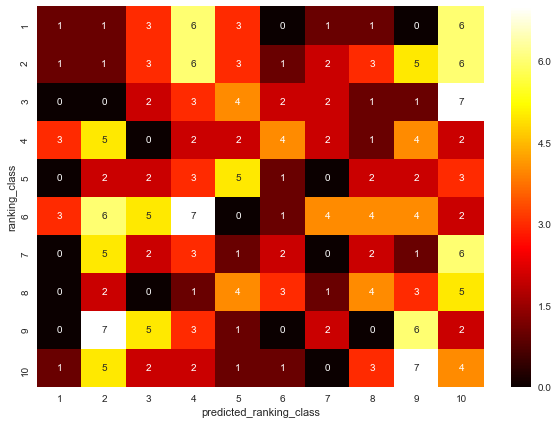
過去にエントリーしたことがある場合
同じ手順で過去にエントリーしたことがある場合のヒートマップも作成します。
is_previous = (predict_result.is_previous == 1)
predict_result_previous = predict_result.loc[is_previous, :]
print(predict_result_previous.shape)
predict_result_previous.head(10)
(845, 7)
| character_id | character_name | prefecture | is_previous | ranking_class | filename | predicted_ranking_class | |
|---|---|---|---|---|---|---|---|
| 0 | 43 | うなりくん | 千葉県 | 1 | 1 | 00000031.jpg | 1 |
| 1 | 166 | ちりゅっぴ | 愛知県 | 1 | 1 | 00002537.jpg | 1 |
| 2 | 619 | トライくん | 大阪府 | 1 | 1 | 00000895.jpg | 2 |
| 3 | 7 | こにゅうどうくん | 三重県 | 1 | 1 | 00000390.jpg | 1 |
| 4 | 326 | 稲敷いなのすけ | 茨城県 | 1 | 1 | 00002736.jpg | 1 |
| 6 | 23 | カミスココくん | 茨城県 | 1 | 1 | 00002620.jpg | 1 |
| 7 | 24 | 福井市宣伝隊長「朝倉ゆめまる」 | 福井県 | 1 | 1 | 00000877.jpg | 1 |
| 8 | 100 | 滝ノ道ゆずる | 大阪府 | 1 | 1 | 00000009.jpg | 1 |
| 9 | 39 | なーしくん | 愛媛県 | 1 | 1 | 00001988.jpg | 1 |
| 10 | 659 | カパル | 埼玉県 | 1 | 1 | 00000364.jpg | 1 |
contingency_previous = pd.pivot_table(
data=predict_result_previous,
index=['ranking_class'],
columns=['predicted_ranking_class'],
values='character_id',
aggfunc='count',
fill_value=0)
sns.heatmap(contingency_previous, annot=True, cmap='hot')
初参加のデータが混じっていた時よりも正の相関がはっきりと分かるようになりました。
やはり、わずかではありますが、右上よりも左下にデータが集まる傾向あります。
考えられる要因は「順位は年を追うごとに連れて下降する」ことです。
また、データは1098件なので、順位帯が1つ違うだけで順位が約100位程度ずれます
予想の精度は低いと言わざるを得ません。
順位は年々下がっていくのかを検証する
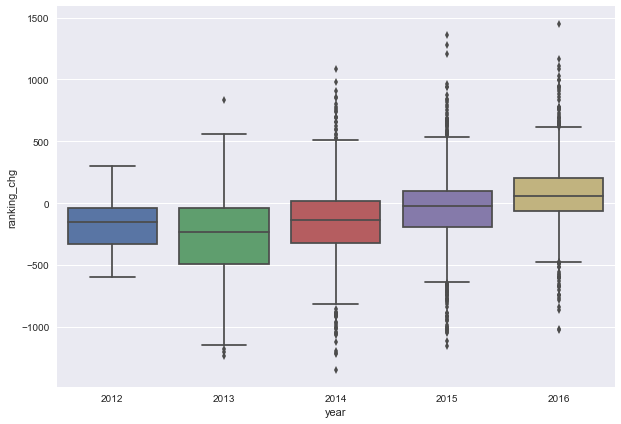
過去の順位よりも下がる傾向を見るために、複数年エントリーしたキャラクターを対象にして過去と現在の順位の差を年度ごとの箱ひげ図で図示します。
今回の学習に使ったデータは次の通りです。
meta_data = pd.read_csv('meta_data_2011_2016.csv')
meta_data.head()
| year | ranking_type | ranking | character_id | character_name | prefecture | |
|---|---|---|---|---|---|---|
| 0 | 2011 | total | 1 | 1 | くまモン | 熊本県 |
| 1 | 2011 | total | 2 | 2 | いまばり バリィさん | 愛媛県 |
| 2 | 2011 | total | 3 | 3 | にしこくん | 東京都 |
| 3 | 2011 | total | 4 | 4 | 与一くん | 栃木県 |
| 4 | 2011 | total | 5 | 5 | はち丸/だなも/エビザベス | 愛知県 |
このデータをもとに過去と現在の順位の差を計算します。
処理は以下の通りです。
ranking_chgは変動した順位で、マイナスは順位が下がったことを示しています。
ranking_data = meta_data[['year', 'ranking', 'character_id', 'character_name']].copy()
ranking_data.sort_values(['character_id', 'year'], inplace=True)
ranking_data.set_index(['year', 'character_id', 'character_name'], inplace=True)
ranking_change = ranking_data.groupby(level=['character_id']).ranking.diff(1)
ranking_change *= -1 # ランキングが下がった場合(順位の値が増加)をマイナスで表示したいため
ranking_change = ranking_change[ranking_change.notnull()]
ranking_change.name = 'ranking_chg'
ranking_change = ranking_change.reset_index()
ranking_change.head()
| year | character_id | character_name | ranking_chg | |
|---|---|---|---|---|
| 0 | 2012 | 2 | いまばり バリィさん | 1.0 |
| 1 | 2012 | 3 | にしこくん | -41.0 |
| 2 | 2013 | 3 | にしこくん | 4.0 |
| 3 | 2012 | 4 | 与一くん | -9.0 |
| 4 | 2013 | 4 | 与一くん | 8.0 |
順位変動の箱ひげ図
sns.boxplot(x='year', y='ranking_chg', data=ranking_change)
2011 ~ 2015年は順位の変動の中央値が0を下回っているため、全体的には順位が過去出場時よりも下がっています。
しかし、2013年までは過去の順位よりも下がる傾向が強まる傾向があったものの、2014年以降は徐々に上がる傾向に転換しているため、やはりトレンドを考慮したモデルを構築するほうが良さそうです。
トレンドが生まれた原因は定かではありませんが、エントリーした各団体がPRを狙って順位が上がる努力をしたということではないかなと考えています。
時間があれば調査してみたいです。
まとめ
正直なところ、時系列に影響されるとは考えていませんでした。
長い目で見ればトレンドはあると思いますが、5〜6年程度では影響ないだろうと決めつけていたためです。
データを収集したら箱ひげ図などで簡単に傾向を掴むというデータ分析では基本的なことを疎かにしてはいけないと、改めて認識しました。
-
こちらにも掲載しています。 https://kishiyama.hatenablog.com/entry/2018/07/06/070000 ↩
-
まずは単純なモデルの構築を目指します。 ↩
-
いわゆる混同行列です。 ↩