はじめに

「Pythonで学ぶ実験計画法入門ベイズ最適化によるデータ解析」によれば、ガウス過程回帰なるものを使うと予測値だけでなく、予測値の分散や標準偏差も得られるので、ベイズ最適化なんてことができるらしい。

今回、RDkitとscikit-learnを使って、化学データによるモデルの構築から、各サンプルの標準偏差の可視化まで行ってみた。

環境

Windows 10
RDKit 2020.09.3
mordred 1.2.0
scikit-learn 0.24.2

モデル構築

データはこちらのデータを利用

https://github.com/hkaneko1985/python_data_analysis_ohmsha/blob/master/sample_data/molecules_with_pIC50.csv

データ読み込み

import numpy as np
import pandas as pd
from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, Descriptors
from rdkit.ML.Descriptors import MoleculeDescriptors
from mordred import Calculator, descriptors

import codecs
with codecs.open('../datas/raw/molecules_with_pIC50.csv', 'r', 'utf-8', 'ignore') as f:
    df = pd.read_csv(f)


# SMILESのリストをMOLに変換
mols = []
for i, smiles in enumerate(smiles_list):
    mol = Chem.MolFromSmiles(smiles)
    if mol:
        mols.append(mol)
    else:
        print("{0} th mol is not valid".format(i))

記述子計算

RDKit記述子計算

descriptor_names = [descriptor_name[0] for descriptor_name in Descriptors._descList]
descriptor_calculator = MoleculeDescriptors.MolecularDescriptorCalculator(descriptor_names)
rdkit_descriptors_results = [descriptor_calculator.CalcDescriptors(mol) for mol in mols]
df_rdkit = pd.DataFrame(rdkit_descriptors_results, columns = descriptor_names, index=names_list)

# 数値変換後のnullの列チェック
df_rdkit = df_rdkit[df_rdkit.columns[~df_rdkit.isnull().any()]]

Mordred記述子計算

# mordredの記述子計算
mordred_calculator = Calculator(descriptors, ignore_3D=True)
df_mordred = mordred_calculator.pandas(pd.Series(mols, index=names_list))

# 数値型への変換
for column in df_mordred.columns:
    if df_mordred[column].dtypes == object:
        #print("{0}/{1}".format(column, df_mordred[column].dtypes))
        df_mordred[column] = df_mordred[column].values.astype(np.float32)
    else:    
        #print("{0}/{1}".format(column, df_mordred[column].dtypes))    
        pass

#数値変換後のnullの列チェック
df_mordred = df_mordred[df_mordred.columns[~df_mordred.isnull().any()]]

データ統合・分割

# RDKit, mordredのプレフィックスをつける(同じ名前の記述子があるため)
for df_tmp, prefix in zip([df_rdkit, df_mordred], ["RDkit.", "Mordred."]):
    columns_new = [(prefix + column_tmp) for column_tmp in df_tmp.columns]
    df_tmp.columns = columns_new

# RDKit, mordredのデータを統合
df_all = pd.concat([df_rdkit, df_mordred], axis=1)

# 目的変数を統合
df_all.insert(0, "t", df["pIC50"].values)


# 学習データとテストデータの分割
from sklearn.model_selection import train_test_split
df_train, df_test = train_test_split(df_all, test_size=0.2, shuffle=True, random_state=43)

# 説明変数と目的変数に分離
train_t = df_train.iloc[:, 0].values
test_t = df_test.iloc[:, 0].values

df_train_X = df_train.iloc[:, 1:]
df_test_X = df_test.iloc[:, 1:]

特徴選択

# 分散が0のものを除去
from sklearn.feature_selection import VarianceThreshold
tmp_values = df_train_X.values
select = VarianceThreshold()
tmp_values = select.fit_transform(tmp_values)

# 同一値が9割以上の記述子を除く

st_threshold = 0.9
selected = []

for column in df_train_X_vt.columns:
    value_counts = df_train_X_vt[column].value_counts(sort=True)
    score = value_counts.values[0]/len(df_train_X_vt[column].values)
    if score < st_threshold:
        selected.append(column)

df_train_X_st = df_train_X_vt[selected]

続いてPandasを活用し相関の高い特徴を除去する(改良)にしたがって相関係数が0.95以上の説明変数の組がある場合、どちらかを除去する。

以降、学習データが df_train_X_ct、テストデータが df_test_X_ct というDataFrameに格納された前提で進める。

オートスケーリング

from sklearn import preprocessing
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
train_X_scaled = ss.fit_transform(df_train_X_ct.values)
test_X_scaled = ss.transform(df_test_X_ct.values)

カーネル選択

下準備ができたので、いよいよscikit-learnのGaussianProcessRegressorを使ってモデルを構築する。

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import DotProduct, WhiteKernel, ConstantKernel, RBF, Matern

# カーネル 11 種類 参考 https://github.com/hkaneko1985/python_doe_kspub/blob/master/sample_program_03_11_gpr_one_kenrnel.py
kernels = [DotProduct() + WhiteKernel(),
           ConstantKernel() * RBF() + WhiteKernel(),
           ConstantKernel() * RBF() + WhiteKernel() + DotProduct(),
           ConstantKernel() * RBF(np.ones(train_X_scaled.shape[1])) + WhiteKernel(),
           ConstantKernel() * RBF(np.ones(train_X_scaled.shape[1])) + WhiteKernel() + DotProduct(),
           ConstantKernel() * Matern(nu=1.5) + WhiteKernel(),
           ConstantKernel() * Matern(nu=1.5) + WhiteKernel() + DotProduct(),
           ConstantKernel() * Matern(nu=0.5) + WhiteKernel(),
           ConstantKernel() * Matern(nu=0.5) + WhiteKernel() + DotProduct(),
           ConstantKernel() * Matern(nu=2.5) + WhiteKernel(),
           ConstantKernel() * Matern(nu=2.5) + WhiteKernel() + DotProduct()]

# 11種類のカーネルで予測
scores = []
for i, kernel in enumerate(kernels):
    gpr = GaussianProcessRegressor(kernel=kernel, random_state=0)
    gpr.fit(train_X_scaled, train_t)
    scores.append(gpr.score(test_X_scaled, test_t))


# 最適なカーネルでモデル構築
kernel = kernels[np.array(scores).argmax()]
gpr = GaussianProcessRegressor(kernel=kernel, random_state=0)
gpr.fit(train_X_scaled, train_t)

この結果、7番目のカーネル関数(ConstantKernel() * Matern(nu=0.5) + WhiteKernel()を使ったモデルが最終モデルとなった。
テストデータでのR^2は0.69であり、まずまずの値が得られた。

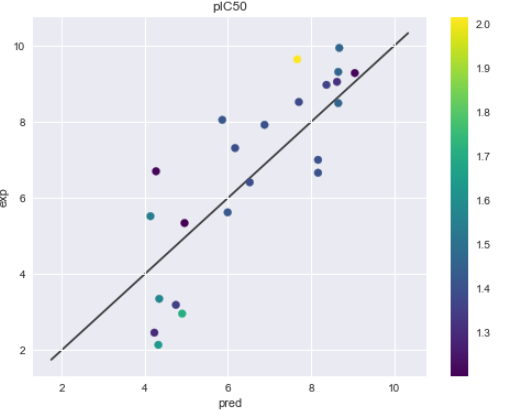
標準偏差を可視化(予測実測プロット)

予測値と標準偏差を元に、予測実測プロットを可視化する。その際に標準偏差に応じて色を変更する。

train_y_with_std = gpr.predict(train_X_scaled, return_std=True)
test_y_with_std = gpr.predict(test_X_scaled, return_std=True)

# 予測実測曲線(テストデータのみ)
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use("seaborn")
figure = plt.figure(figsize=(8, 6))
ax = figure.add_subplot(1,1,1)
sc = ax.scatter(test_y_with_std[0], test_t, c=test_y_with_std[1],cmap=plt.cm.viridis)
ax.set_title("pIC50")
ax.set_xlabel("pred")
ax.set_ylabel("exp")

lims = [
    np.min([ax.get_xlim(), ax.get_ylim()]),  # min of both axes
    np.max([ax.get_xlim(), ax.get_ylim()]),  # max of both axes
]

ax.plot(lims, lims, 'k-', alpha=0.75, zorder=0)
plt.colorbar(sc)

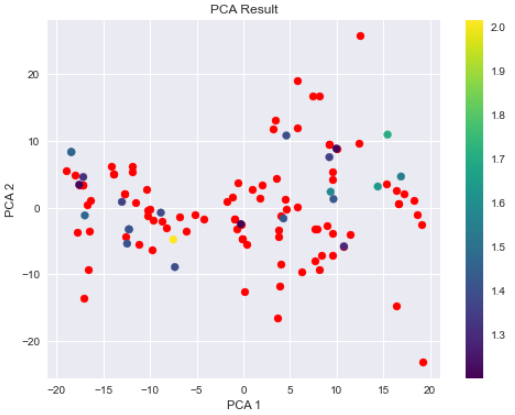
標準偏差を可視化(主成分分析)

学習データ上に対するテストデータの散らばり具合と、それによる標準偏差の変動をざっくりみたいので、学習データとテストデータについて、主成分分析をして可視化してみる。

from sklearn.decomposition import PCA 
pca_model = PCA(n_components=2)
Z_train = pca_model.fit_transform(train_X_scaled)
Z_test = pca_model.transform(test_X_scaled)
figure = plt.figure(figsize=(8, 6))
ax_pca = figure.add_subplot(111)
#ax_pca.scatter(Z_train[:, 0], Z_train[:, 1], c=train_y_with_std[1], cmap=plt.cm.viridis)
ax_pca.scatter(Z_train[:, 0], Z_train[:, 1], c="red")
ax_pca.scatter(Z_test[:, 0], Z_test[:, 1], c=test_y_with_std[1], cmap=plt.cm.viridis)
ax_pca.set_title("PCA Result")
ax_pca.set_xlabel("PCA 1")
ax_pca.set_ylabel("PCA 2")
plt.colorbar(sc)

赤が学習データで、テストデータのみ標準偏差により色付けしている。
学習データと重なるぐらい近いテストデータは、標準偏差が小さい(濃い色)になっていることが分かる。

感想

前回 LightGBMでハイパーパラメータチューニングをした場合と、同程度の精度のカーネルが得られたので少々びっくりした。標準偏差も得られる分、こちらのモデルの方が情報量が多い。
今後ガウス過程回帰を用いてベイズ最適化を行ってみたい。

参考

sklearn.gaussian_process.GaussianProcessRegressor

RDkitとscikit-learnで化学データによるガウス過程回帰を試してみる