プロ野球:1位を当ててみた！～ロジスティック回帰で

はじめに

最近ヤクルトが強いですね～ヤクルト1強みたいな感じになってますね。

ヤクルトの強さってどこに現れるんだろう？

これが気になって、モデルを作ってみました。
今回は打率といった野球の様々な指標から、その球団が1位かどうかを
ロジスティック回帰モデルを使って予測させました。

データ収集

以下のサイトから過去のデータを引用しました。
https://baseball-data.com/team/hitter.html

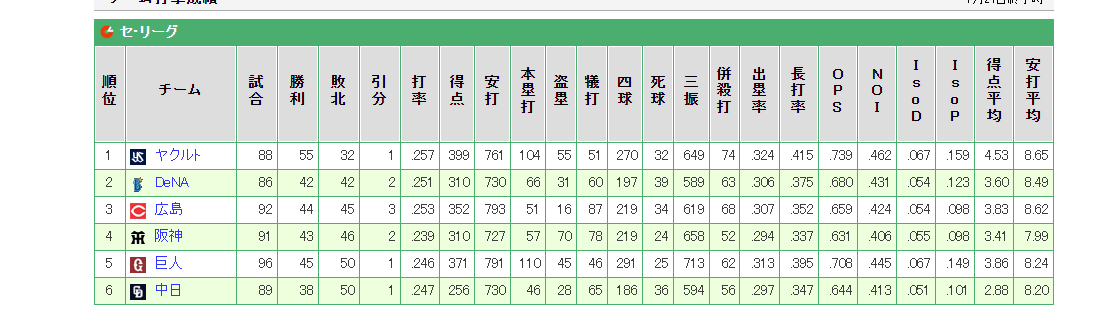
↑こんな感じで各球団の打率、得点等の統計データがあります。
今回は2009年～2021年における、セ・リーグのチーム打撃成績とチーム投手成績を収集しました。
webページの表データを自動で抽出するには、pandasのread_htmlを利用します。

baseball_data_from_url.py

import pandas as pd
HP=["hitter","pitcher"]#打撃か投手成績かを変数にする。
for hp in HP:
 for i in range(9,22):#2009年~2021年まで繰り返す。
  url='https://baseball-data.com/{0}/team/{1}.html'.format(i,hp)
  data = pd.read_html(url, header = 0)[0]#0ならセ・リーグ
  data.to_csv('./baseball/{0}/{0}_{1}.csv'.format(hp,i+2000) ,encoding='utf_8_sig')#csvをフォルダに格納 

上記コードで年度別、打撃投手別にデータを収集できたので、次はこれらを1つにまとめます。
ここの作業については細かいのでコードは省きます(mergeとかconcatとか使いました)。
最終的に以下のようなcsvファイルを得ました。

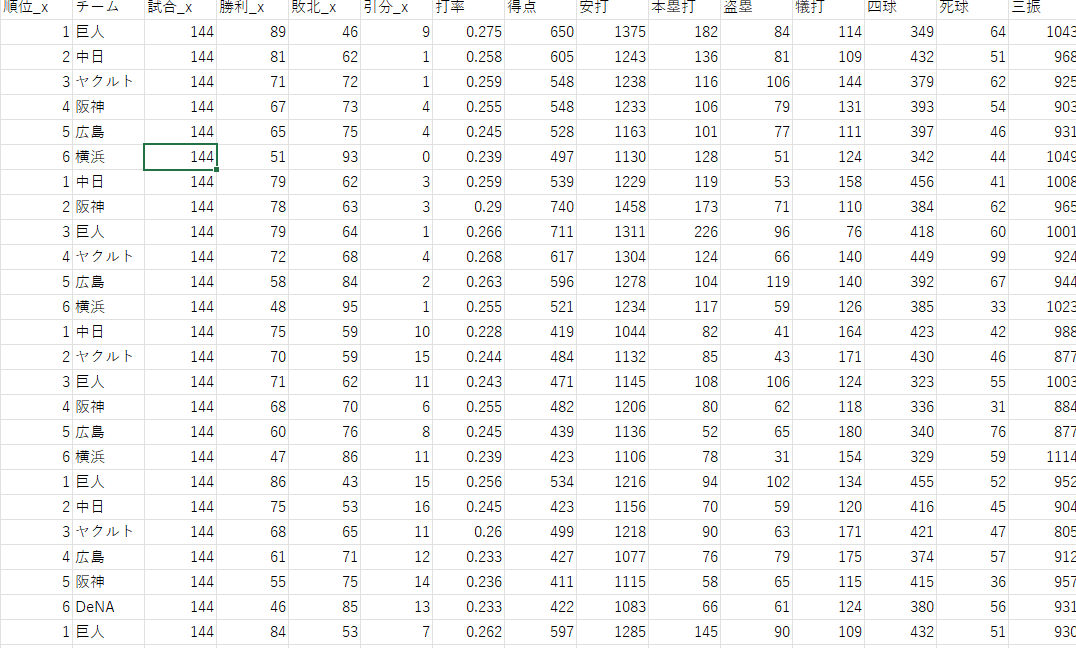
データ加工

続いて、データ加工です。以下の3つを行いました。
➀収集したデータからいらない変数を除外
②データの標準化
③順位ラベル付け
➀で除外したものは、順位、試合数、勝利数、敗北数、引き分け数です。これらは順位を決めるうえで直接使う値であるため、
除外しました。
②の標準化は平均0、分散1になるように行いました。
③順位ラベルは、今回は1位だけ当てたいので、1位の球団には1をそれ以外は0になるようにつけました。
最終的には、今回使うデータは34変数で、データ数は6球団×13年分=78個となりました。

モデル構築

モデルとしてロジスティック回帰を使いました。式は以下の通りです。$p$は確率です。

p=\frac{1}{1+\exp(-y)} \\
y=\beta_0+\beta_1x_1+\beta_2x_2・・・\beta_nx_n

ロジスティック回帰は複数の説明変数から、確率を予測するときに使われます。
説明変数$x$は先ほど収集した34種類の野球統計データで、目的変数$p$は順位ラベル(1位なら1,それ以外は0)となります。
ロジスティック回帰では回帰係数$\beta$の符号や大きさをみることで、目的変数とどのような関係性があるのか解釈することが出来ます。なお、ロジスティック回帰を使う上で、説明変数が34個もあるのは共線性の問題からしてマズイところもあるかもしれませんが、これは研究ではないのではそこは気にしてません。研究なら気にします。
ではコードです。

logistic.py

data=pd.read_csv('./baseball/all_data_stand.csv')
X=data.loc[:, '打率':'被安平均']#説明変数
Y=data['順位ラベル']#目的変数
lr = LogisticRegression() # ロジスティック回帰モデルのインスタンスを作成
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2, random_state =None) # 80%のデータを学習データに、20%を検証データにする
lr.fit(X_train, Y_train) # ロジスティック回帰モデルの重みを学習
# 推論
Y_pred = lr.predict(X_test)
#回帰係数を出力
df_model = pd.DataFrame(index=X.columns)
df_model["偏回帰係数"] = lr.coef_[0]
print(df_model)
# 正解率
print('accuracy: ',  round(accuracy_score(y_true=Y_test, y_pred=Y_pred),2))
# 適合率
print('precision: ', round(precision_score(y_true=Y_test, y_pred=Y_pred),2))
# 再現率
print('recall: ',    round(recall_score(y_true=Y_test, y_pred=Y_pred),2))
# f1スコア
print('f1 score: ',  round(f1_score(y_true=Y_test, y_pred=Y_pred),2))
#モデルを保存
filename = './baseball_model.pkl'
pickle.dump(lr,open(filename,'wb'))

結果

予測精度を測る指標として正答率だけでは不十分なので、他の指標も取り入れました。
結果は以下の通りです。

指標	accuracy	precision	recall	f1 score
score	0.94	0.8	1.0	0.89

結果はどれも非常に高い数値でした。使ったデータの内、ラベルが1のデータは全体の1/6なので(6球団の内1位は1球団だけだから)、仮にモデルが全部0と予測してしまっても、accuracyは5/6=0.83と、高い数値になります。一方で、このような予測をした場合、recall=0となります。つまりaccuracyだけでは評価指標として十分でないことがあるのですが、このモデルはどの指標でも高い数値が出ているので、偏った予測はしてないでしょう。
続いて回帰係数になります。以下は回帰係数の絶対値の大きい順に並べています。

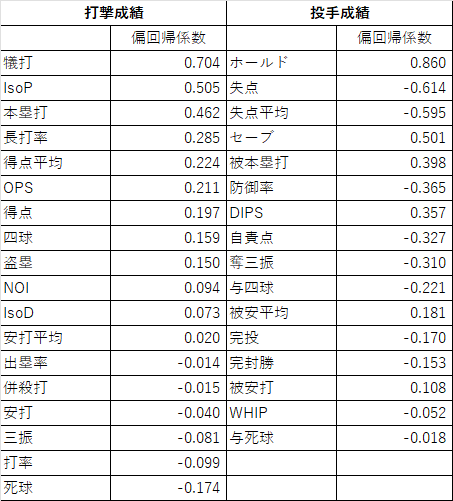
打撃成績に関する変数では、犠打、ISOP、本塁打が高いですね。ちなみにISOPは純粋な長打力を表し、長打率と打率の差で計算されます。点数に必ずしも直結しない犠打が一番高いのは意外ですね。符号を見ると大体正になっていますが、これは自然な結果ですね。例えば、本塁打の符号は正ですが、これは本塁打の本数が多いほど1位になる確率が上がることを意味します。
投手成績についてはホールド、失点、防御率などが高いですね。ホールドは試合のリードや試合の状況を保った投手に記録される指標です。つまりホールドの回数が多いほど、勝利への貢献が大きいと判断できます。その意味では符号が正なのは自然ですね。一方で失点、防御率は大きいほど勝利への貢献が小さくなると考えられるので、符号が負なのは納得できますね。
＊本来であれば、各回帰係数について、0と有意に異なるかを$p$値を使って評価し、変数として採用するか判断します。しかしsklearnには$p$値を算出する機能が無かったため、ここではそういった議論はしていません。

2022年データ予測

最後に2022年の今の段階でのデータを使って、順位予測をしてみました。

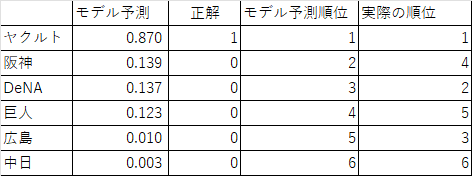
モデルの予測値が高い順に並べています。やはりモデルはヤクルトを高く予測しています。圧倒的ですね。
面白いのが、2位の広島がモデルでは4位評価されているところですね。これはこれまでの戦績の割に順位が良いということですね。一方で現在4位の阪神はモデルでは2位に評価されています。阪神は戦績自体は悪くないようですが、それが実際の順位に反映されていないようですね。

最後に

野球はサッカーのような公式賭博が無いので、これが何かの役に立つかは不明ですが。。。
面白かったので良し！