Mahalanobis'距離と確率楕円の関係を書こうと思ったら、
思いの外、理論的背景が長くなったのでここで分けておきます。
Mahalanobis' Distance
点Xと群Aのマハラノビス距離は、下記で定義される。
D_{Mahalanobis}^2 = (X-\bar{A})^t cov(A) ^{-1}(X-\bar{A}) \\
\ \\
\begin{eqnarray}
cov(A):& &variance\ covariance\ matrix \\
\bar{A}:& &mean(A)\\
^t:& &transported\ matrix\\
^{-1}:& &inverse\ matrix \\
\end{eqnarray}
概念
2次元の場合を考える。
前回紹介した確率楕円の考え方を押さえておく。
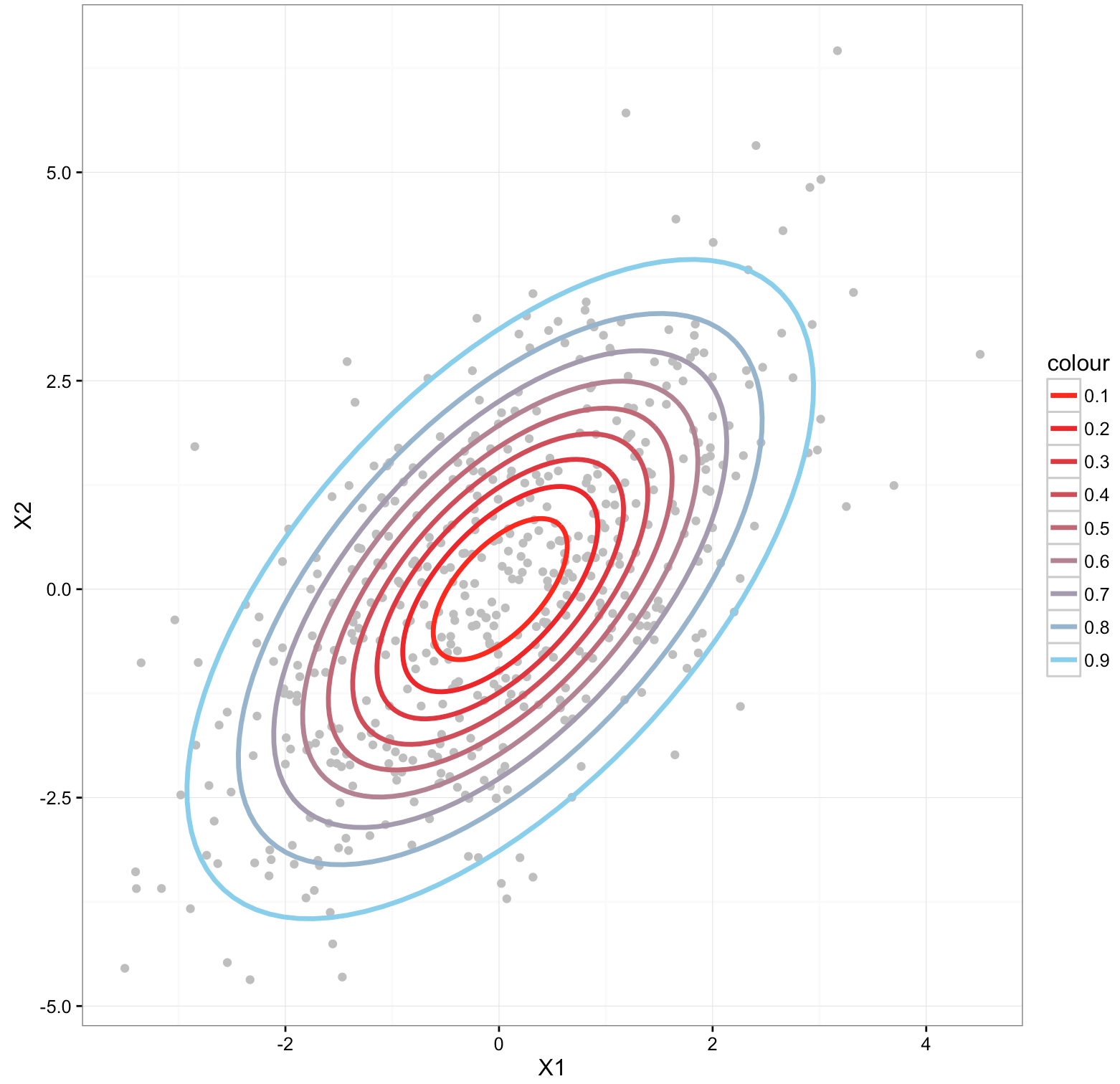
二次元正規分布を例にして、中心からhoge%のプロットが含まれる範囲を描画してあります。
(RコードはAppendix-1)
ポイントは、同じ色の楕円上の点は同等に扱いたい、という事です。
このままでは、分布の中心(原点)からの距離が均等ではない。
そこで、補正をかけて下図のように変換したい。
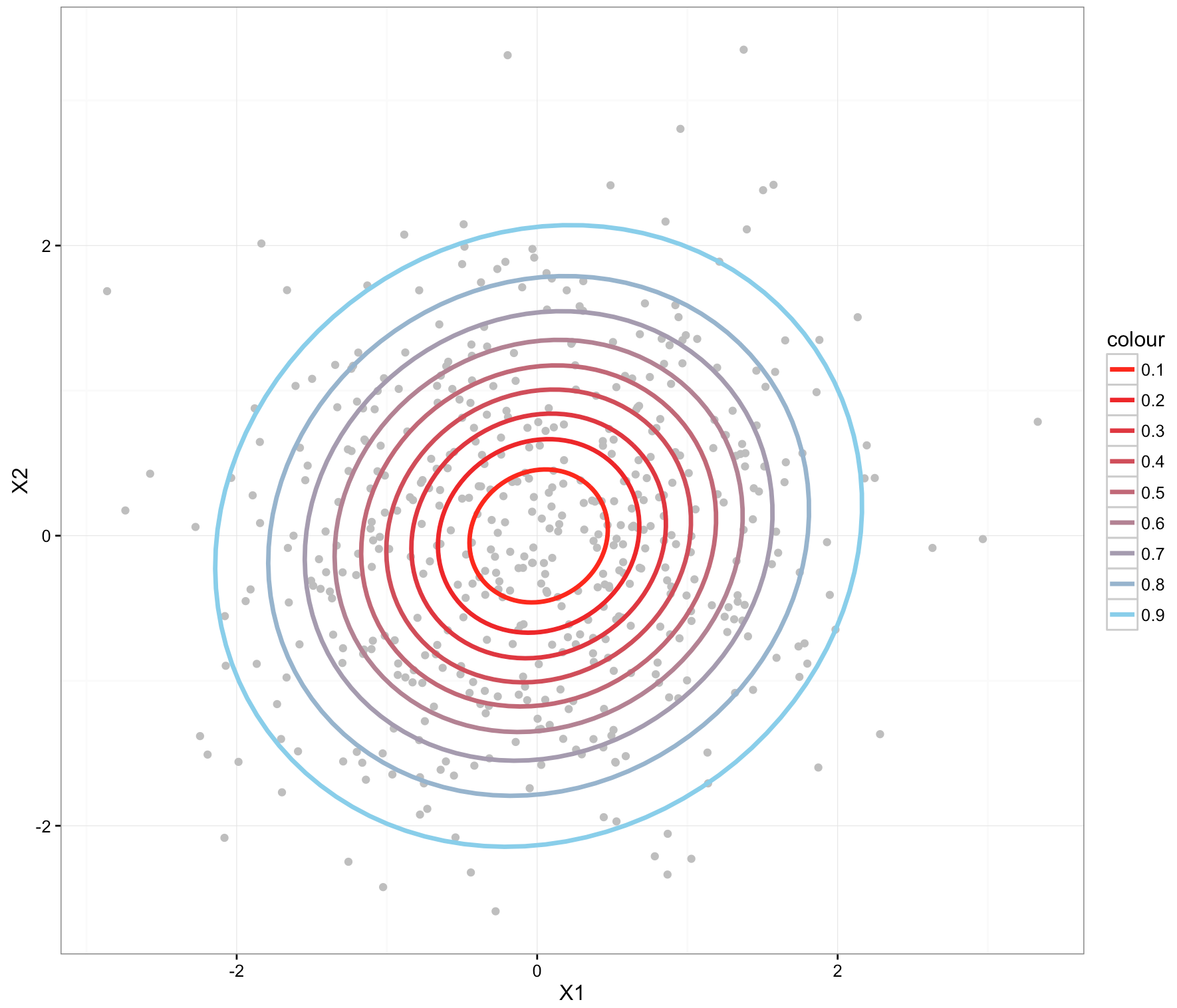
2つの補正を行います。
・"長軸"をX軸、"短軸"をY軸に一致するように回転補正
・各軸方向に分散=1になるように補正
で、補正後のプロットと中心の距離のことを、Mahalanobis'距離と言います。
勘所の鋭いヒトは、これって主成分分析じゃん、と思うはずです。
その通り、でして、Mahalanobis'距離を求めるということは、分散共分散行列に基づく主成分分析をして、その主成分でプロットをスケールする、という事と同等の操作をしています。
数学的意味
投射先の軸上の分散
座標(X, Y)をθ度回転させた座標(X',Y')は、
\begin{eqnarray}
X' &=& &cosθ*X &+ sinθ*Y \\
Y' &=& -&sinθ*X &+ cosθ*Y
\end{eqnarray}
つまり回転したい向きの方向ベクトル(cosθ, sinθ)が分かれば良い。
どうやってθを決定すれば良いかというと、分布の"長軸"なわけなので、
その軸に投射した時に分散が最大になる軸を選べば良い。
少し記号を変えて、投射前座標(X1,X2)を方向ベクトル(h1,h2)の軸に投射した座標をYとします。
Y=h_1*X_1+h_2*X_2
軸上の座標の標本平均は、
\begin{eqnarray}
\bar{Y}&=&\frac{1}{n}\sum_{i=1}^n{Y_i}=\frac{1}{n}\sum_{i=1}^n{(h_1X_1+h_2X_2)} \\
&=&\frac{1}{n}\sum_{i=1}^n{h_1X_1}+\frac{1}{n}\sum_{i=1}^n{h_2X_2} \\
&=&h_1\bar{X_1}+h_2\bar{X_2}
\end{eqnarray}
これを用いて、軸(h1,h2)上の標本分散は、
\begin{eqnarray}
s^2_{(h_1, h_2)}
&=&\frac{1}{n-1}\sum_{i=1}^n{(Y_i-\bar{Y})^2} \\
&=&\frac{1}{n-1}\sum_{i=1}^n{ \Big\{(h_1X_{i1}+h_2X_{i2})-(h_1\bar{X_1}+h_2\bar{X_2}) \Big\}^2 } \\
&=&h_1^2 \frac{1}{n-1}\sum_{i=1}^n{(X_{i1}-\bar{X_1})^2}
+2h_1h_2\frac{1}{n-1}\sum_{i=1}^n{(X_{i1}-\bar{X_1})(X_{i2}-\bar{X_2})}
+h_2^2 \frac{1}{n-1}\sum_{i=1}^n{(X_{i2}-\bar{X_2})^2} \\
&=& h_1^2\ s_{11}+2h_1h_2\ s_{12}+h_2^2\ s_{22}
\end{eqnarray}
え〜と、初項から、X1の標本分散s11、X1,X2の標本共分散s12、X2の標本分散s22の形になっているという事です。
つーことで、
S= \left(
\begin{array}{cc}
s_{11} & s_{12} \\ s_{12} & s_{22}
\end{array} \right),
h= \left( \begin{array}{c} h_1 \\ h_2 \end{array} \right)
分散共分散行列Sと方向ベクトルhを用いて、
s^2_{(h_1, h_2)} = h^t Sh
このhが主成分の固有ベクトルだったとすると、
\begin{equation}
(S-λE)h=0
\Rightarrow h^t Sh = λ = s^2_{(h_1, h_2)}
\end{equation}
なる固有値λが存在する(Eは単位行列)。
すなわち、主成分軸方向の分散は、対応する固有値に一致する。
(あとで、ここに戻ってきます)
Mahalanobis'距離
で、求めたい値は、
- 元座標
(X1, X2)を固有ベクトルh1(h11, h12)とh2(h21,h22)を使って主成分座標(pX1, pX2)に変換 - 主成分座標
(pX1, pX2)と中心の距離を固有値λ(λ1,λ2)のルートで割った距離を算出
という事になる。
元座標(X1, X2)は、中心原点(0,0)に平行移動しておくものとします。(回転の関係で)
さて、2から攻めると、
\begin{eqnarray}
D^2_{mahalanobis}
&=& \frac{pX_1^2+pX_2^2}{s^2}\\
&=& \frac{pX_1^2+pX_2^2}{λ}\\
&=& ( \begin{array}{cc}pX_1 & pX_2 \end{array} )
\Big( \begin{array}{c} \frac{pX_1}{λ_1} \\ \frac{pX_2}{λ_2} \end{array} \Big) \\
&=& ( \begin{array}{cc}pX_1 & pX_2 \end{array} )
\Big( \begin{array}{cc} \frac{1}{λ_1} & 0\\ 0 & \frac{1}{λ_2} \end{array} \Big) ( \begin{array}{cc}pX_1 & pX_2 \end{array} )^t
\\
\end{eqnarray}
1を盛り込む。
pX_1 = h_{11} X_1+h_{12}X_2\\
pX_2 = h_{21} X_1+h_{22}X_2
より、
\begin{eqnarray}
( \begin{array}{cc}pX_1 & pX_2 \end{array} ) &=&
( \begin{array}{cc}X_1 & X_2 \end{array} )
\Big( \begin{array}{cc} h_{11} & h_{21}\\ h_{12} & h_{22} \end{array} \Big) \\
& \equiv &
( \begin{array}{cc}X_1 & X_2 \end{array} )H
\end{eqnarray}
Hは固有ベクトルマトリックス。
また、
( \begin{array}{cc}pX_1 & pX_2 \end{array} )^t =
H^t
( \begin{array}{cc}X_1 & X_2 \end{array} )^t \\
これらを用いて、
\begin{eqnarray}
D^2_{mahalanobis}
&=& ( \begin{array}{cc}pX_1 & pX_2 \end{array} )
\Big( \begin{array}{cc} \frac{1}{λ_1} & 0\\ 0 & \frac{1}{λ_2} \end{array} \Big) ( \begin{array}{cc}pX_1 & pX_2 \end{array} )^t
\\
&=& ( \begin{array}{cc}X_1 & X_2 \end{array} )
H
\Big( \begin{array}{cc} \frac{1}{λ_1} & 0\\ 0 & \frac{1}{λ_2} \end{array} \Big)
H^t
( \begin{array}{cc}X_1 & X_2 \end{array} )^t
\end{eqnarray}
大丈夫ですか?
ページトップの数式と見比べてください。大分近づいてきました。
あとは、
H
\Big( \begin{array}{cc} \frac{1}{λ_1} & 0\\ 0 & \frac{1}{λ_2} \end{array} \Big)
H^t
\equiv S^{-1}
が言えればOKですね?
少しトリッキーですが、
\begin{eqnarray}
\Big( \begin{array}{cc}
\frac{1}{λ_1} & 0\\ 0 & \frac{1}{λ_2}
\end{array} \Big)
&=&
\Big( \begin{array}{cc}
\frac{λ_2}{λ_1λ_2} & 0\\ 0 & \frac{λ_1}{λ_1λ_2}
\end{array} \Big) \\
&=&
\frac{1}{λ_1λ_2}
\Big( \begin{array}{cc} λ_2 & 0\\ 0 & λ_1 \end{array} \Big) \\
&=&
\Big( \begin{array}{cc} λ_1 & 0\\ 0 & λ_2 \end{array} \Big)^{-1} \\
&\equiv& \Lambda^{-1}
\end{eqnarray}
と置く。
λ大文字は、対角成分が固有値の行列です。
H \Lambda^{-1} H^t \equiv S^{-1}
が言えればOK。Sは分散共分散行列。
ふ〜。さて、(あとでここに)と言っていた式を再掲。
(S-λE)h=0
これを今風の記号に書き直すと、
(S-λ_1 E)\Big(\begin{array}{c}h_{11}\\ h_{12}\end{array}\Big)=0 \\
(S-λ_2 E)\Big(\begin{array}{c}h_{21}\\ h_{22}\end{array}\Big)=0
これを少し整理して、
S\Big(\begin{array}{c}h_{11}\\ h_{12}\end{array}\Big) = λ_1\Big(\begin{array}{c}h_{11}\\ h_{12}\end{array}\Big)\\
S\Big(\begin{array}{c}h_{21}\\ h_{22}\end{array}\Big)=
λ_2\Big(\begin{array}{c}h_{21}\\ h_{22}\end{array}\Big)
何がしたいかというと、
\begin{eqnarray}
S \Big(\begin{array}{cc}h_{11} & h_{21} \\ h_{12} & h_{22} \end{array} \Big)&=&
\Big(\begin{array}{cc}λ_{1}h_{11} & λ_2h_{21} \\ λ_1h_{12} & λ_2h_{22} \end{array} \Big) \\
&=&\Big(\begin{array}{cc}h_{11} & h_{21} \\ h_{12} & h_{22} \end{array} \Big)
\Big(\begin{array}{cc}λ_1 & 0 \\ 0 & λ_2 \end{array} \Big)
\end{eqnarray}
すなわち、
SH=H \Lambda
これを用いて、
\begin{eqnarray}
SH&=&H \Lambda \\
S^{-1}SH&=&S^{-1}H\Lambda \\
H&=&S^{-1}H\Lambda \\
H\Lambda^{-1}&=&S^{-1}H\Lambda \Lambda^{-1}=S^{-1}H\\
H\Lambda^{-1}H^{-1}&=&S^{-1}HH^{-1}=S^{-1}
\end{eqnarray}
おっと、ここで、
\begin{eqnarray}
H^tH&=&
\Big( \begin{array}{cc} h_{11} & h_{12} \\ h_{21} & h_{22} \end{array} \Big)
\Big( \begin{array}{cc} h_{11} & h_{21} \\ h_{12} & h_{22} \end{array} \Big)\\
&=& \Big( \begin{array}{cc} h_{11}^2+h_{12}^2 & h_{11}h_{21}+h_{12}h_{22} \\
h_{11}h_{21}+h_{12}h_{22} & h_{21}^2+h_{22}^2 \end{array} \Big) \\
&=&\Big( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \Big) \\
\therefore H^t&=&H^{-1}
\end{eqnarray}
対角成分=1は、単位ベクトルだから。
それ以外の成分=0は、直行ベクトルだから。
やっとなっ、
H\Lambda^{-1}H^{t}=S^{-1}
従って、
\begin{eqnarray}
D^2_{mahalanobis}
&=& ( \begin{array}{cc}X_1 & X_2 \end{array} )
H \Lambda^{-1} H^t
( \begin{array}{cc}X_1 & X_2 \end{array} )^t\\
&=& ( \begin{array}{cc}X_1 & X_2 \end{array} )
S^{-1}
( \begin{array}{cc}X_1 & X_2 \end{array} )^t
\end{eqnarray}
っという事になりました。
Appendix
Appendix-1. 確率楕円
詳しくは前回
library("ellipse")
library("ggplot2")
# "回転前"のデータ
set.seed(13)
dat0 <- matrix(rnorm(1000), , 2)
# 回転
sita <- pi/4
rot <- matrix(c(cos(sita), -sin(sita), sin(sita), cos(sita)),2)
dat <- data.frame(dat0 * c(2, 1) %*% rot)
# 楕円を描く確率水準
level <- seq(0.1, 0.9, by=0.1)
# 楕円座標の算出
datE <- NULL
for(i in level){
datE <-rbind(datE, cbind(i, ellipse(cov(dat), centre=apply(dat, 2, mean), level=i)))
}
datE <- data.frame(datE)
datE$i <- factor(datE$i)
# カラーコードの設定
Col <- colorRamp(c("Red","skyblue"))
color <- rgb(Col(seq(0, 1, length=length(level)))/255)
# 軸範囲
ax <- max(abs(dat))
# 描画
ggplot()+
layer(
data = dat,
mapping = aes(x=X1, y=X2),
geom = "point",
stat = "identity",
position = "identity",
params = list(color="grey")
)+
layer(
data = datE,
mapping = aes(x=X1, y=X2, color=i),
geom = "path",
stat = "identity",
position = "identity",
params = list(size=1.2)
)+
xlim(-ax, ax)+
ylim(-ax, ax)+
scale_color_manual(values=color)+
theme_bw()
っとまぁ、最近はggplot2を使うようにしていますが、普通にplotを使っても書けます。
# ggplot2を使わない描画
par(mar=c(2,2,1,1))
plot(0,0,type="n", xlim=c(-ax,ax), ylim=c(-ax,ax), mgp=c(2, 0.3, 0), tcl=-0.2)
points(dat, col="grey", pch=16)
for(i in 1:length(level)){
lines(datE[datE$i==level[i], 2:3], col=color[i], lwd=2)
}
ん〜。どちらが見直した時に読みやすいか、の好みで。
plotも、結構使い勝手いいと思いますよっ。
参考文献
- 静岡大 金久保先生のページより、判別分析(マハラノビス)
- 書籍ですが、『多次元データ解析法(Rで学ぶデータサイエンス)』