スモール・ワールド
「6次の隔たり」とか「ケビン・ベーコン数」とか「エルディシュ数」とか。
知り合いの、知り合いの、知り合いの、知り合いの、知り合いの、知り合い、まで辿ると、全世界のヒトを網羅するという都市伝説です。
ん〜、という事は。
世界人口が80億人ぐらいとして、1/6乗は、約30人。
これは家族・親戚も含めているので、そうですね、6人ぐらい引いておきます。24人。
男女比は半々として、恋愛対象になるセクシュアリティを持つのは概ね半数。12人。
恋愛対象年齢の幅は、ヒトそれぞれですが、ザックリ半分にします。6人。
つまり、気になるあのヒトを巡って、あなたが争うべき相手は、全世界で概ね5人です。
もちろん、この繋がりは動的平衡にあるので、概ね5人は入れ替わり立ちかわるはずですが。
おっと、道ならぬ恋に足を踏み入れる覚悟が無いのならば、すでにパートナがいる、そうですね、約半数を除けるので概ね2人ですね。
なんのこっちゃ。
世界は小さいという事です。
大きさは、構造と機能の2つの方向から定義する事ができます。
例えば、日本にいるAさんと、パタゴニア平原にいる親友のBさんとは、構造(物理)的には大きく離れていても、電話番号さえ知っていればいつでも連絡を取る事ができるでしょう(電話と電話代さえあれば)。つまり、機能的には1つのパスで繋がる。
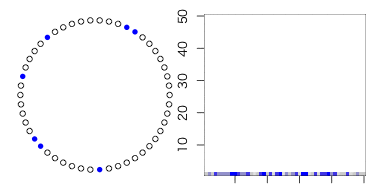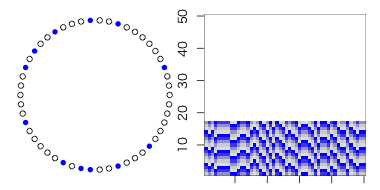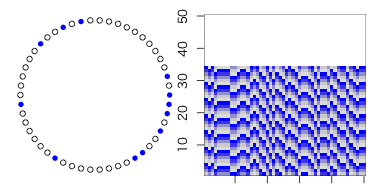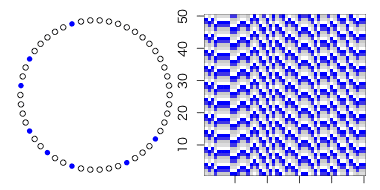
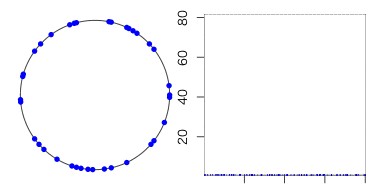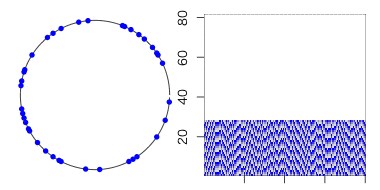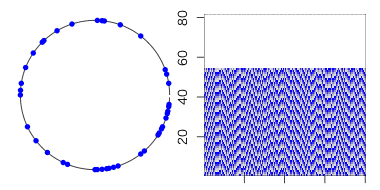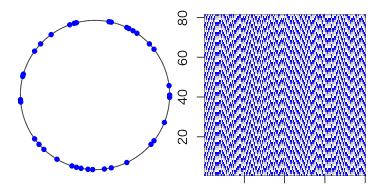
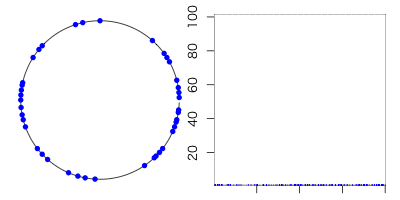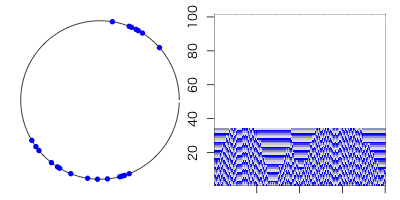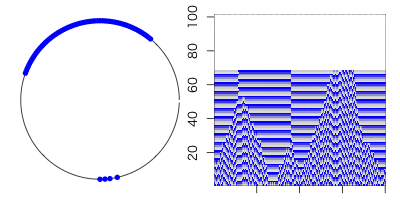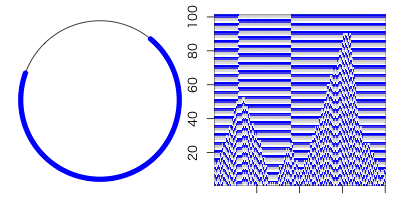
例えば、これは100人の独居引きこもりワールドです。
全ての点と点は、機能的に完全に独立です。
ただ、time-stepが5過ぎる毎に青くなる。
非常に規則的な繋がりを持った世界を考えてみましょう。
例えば、「近傍の$k$人(両側の$k/2$人)」と繋がっている世界ではどうでしょうか。
繋がっているというのは、独立では無い、影響を受ける、という事です。
ここでは多数決を採用しましょう。
繋がっている相手のうち半数以上が青だったら、自分も青になる。
という法則を導入します。
この時、世界はどう振る舞うのか?想像できますか?
βモデル
非常にシンプルで(、従って)クールな世界のモデルが、βモデルです。
詳細は、スモールワールド, D. Wattsをご参照ください。素晴らしい本です。
ネットでは、この資料とかが分かりやすいかも。
エッセンスは、「規則的な世界」と「ランダムな世界」を連続的に記述したいという事です。
近傍k人と規則的に繋がっている状態からスタートし、
・1つの頂点の1つの辺を選び、
・確率βで、繋がる相手をランダムな頂点に繋ぎ変える。
・この操作をもとからあった全ての辺に適用するまで繰り返す。
・ただし、自分自身と繋がる事や、すでにある辺に重なる事は無い。
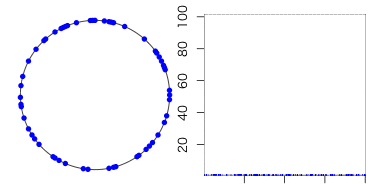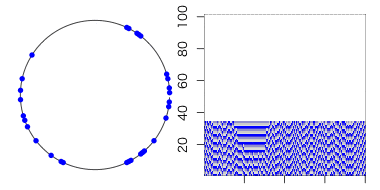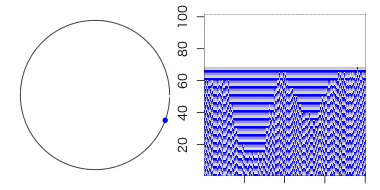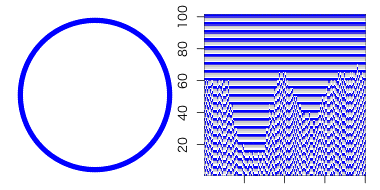
β=0なら繋ぎ変わら無いので「規則的な世界」。
β=1ならば全てがランダムな辺になるので「ランダム(に近い)世界」が実現する。
という事は、その間の値を取れば、「規則とランダムの狭間」の世界を表現できるハズ。
重複が無いので、ネットワーク全体が持つパスの数は不変。
また、この繋がりが「双方向」である事に注意してください。
Rによる実装
ベタ打ちです。ベッタベタです。
そう。迷える子羊よ、恐れるものは何も無い。
汝には $for$文 があるのです。
録画はgifにしたかったので、animation::saveGIFを使いました。
落とし穴だったのは、βモデルでは(系としてのパス数は不変だけど)それぞれのノードが持つパスの数は、一般に、均等では無いという事。あと、双方向なのも面倒でしたね。
結果
共通のパラメータは
population <- 200 # プロットの数
t.max <- 100 # 時間の終点
n.step <- 5 # 1回の"発火"に至るまでのステップ数
n.bond <- 16 # β=0の時、1つのプロットが持つpathの数
あ、β=1だけt.max=80ですね(大人の事情)。
ソースコードはAppendixにまとめました。
Enjoy!!!
Appendix
初期値
population <- 200 # プロットの数
t.max <- 100 # 時間の終点
n.step <- 5 # 1回の"発火"に至るまでのステップ数
n.bond <- 16 # β=0の時、1つのプロットが持つpathの数
beta <- 1 # β=1でlattice, β=0でrandomネットワーク
βモデルシミュレーション用関数
cycle_beta <- function(population=population, t.max=t.max,
n.step=n.step, n.bond=n.bond, beta=beta){
sita <- seq(0, 2*pi*(1-1/population), length=population)
x <- cos(sita); y <- sin(sita)
ID <- 1:population
a <- rep(ID, 2)
b <- matrix(runif(population*n.bond/2), population)
bond_beta <- mapply(rep, 1:population, 0)
for(k in 1:population){
for(j in 1:(n.bond/2)){
if(b[k, j] <= beta){
target <- sample(ID[!is.element(ID, c(k, bond_beta[[k]]))], 1)
bond_beta[[k]] <- c(bond_beta[[k]], target)
bond_beta[[target]] <- c(bond_beta[[target]], k)
}else{
target <- a[k+j]
bond_beta[[k]] <- c(bond_beta[[k]], target)
bond_beta[[target]] <- c(bond_beta[[target]], k)
}
}}
stat <- sample(1:n.step, population, replace=T)
stat_all <- stat
for(i in 1:t.max){
stat <- stat + 1
stat[stat > n.step] <- 1
stat1 <- stat
for(k in 1:population){
input <- stat[bond_beta[[k]]]
if(sum(input==n.step) >= (length(input)/2)){
stat1[k] <- n.step
}
}
stat_all <-cbind(stat_all, stat1)
stat <- stat1
}
Col <- colorRamp(c("grey95", "grey80", "blue"))
image(stat_all, col=rgb(Col(1:n.step/n.step)/255), ann=F, axes=F)
return(stat_all)
}
録画用関数定義
cycle <- function(stat_all=stat_all){
par(mfrow=c(1, 2), mar=c(1, 1, 1, 1))
for(i in 1:(t.max+1)){
# 円形プロットの描画
plot(x, y, type="n", axes=F, xlab="", ylab="")
lines(x, y)
points(x[stat_all[,i] == n.step], y[stat_all[,i] == n.step],
pch=16, col="Blue")
# imageの描画
stat_image <- stat_all
if(i <= t.max){ stat_image[, (i+1):ncol(stat_image)] <- 0 }
Col <- colorRamp(c("grey95", "grey80", "blue"))
image(x=1:population, y=1:(t.max+1), z=stat_image,
col=c("white", rgb(Col(1:n.step/n.step)/255)))
}
}
録画キックコード
library("animation")
stat_all <- cycle_beta(population, t.max, n.step, n.bond, beta)
saveGIF({
ani.options(interval = 0.05,
convert = "/opt/ImageMagick/bin/convert")
cycle.simple()},
movie.name="hoge.gif",
ani.width=380, ani.height=190, clean=T
)