『カーネル多変量解析』 赤穂昭太郎 (岩波書店)
手を動かして図を再現するのは初学者の常套手段として。
とりあえず1章の図4枚をRで作ってみる。
私は、手を動かす時はネチネチ泥臭く組んでみるようにしています。
解析に今すぐ使いたい方は、格好良く{kernlab}を使った例が↓。
http://www.slideshare.net/yokkuns/tokyor45
カーネル関数の例
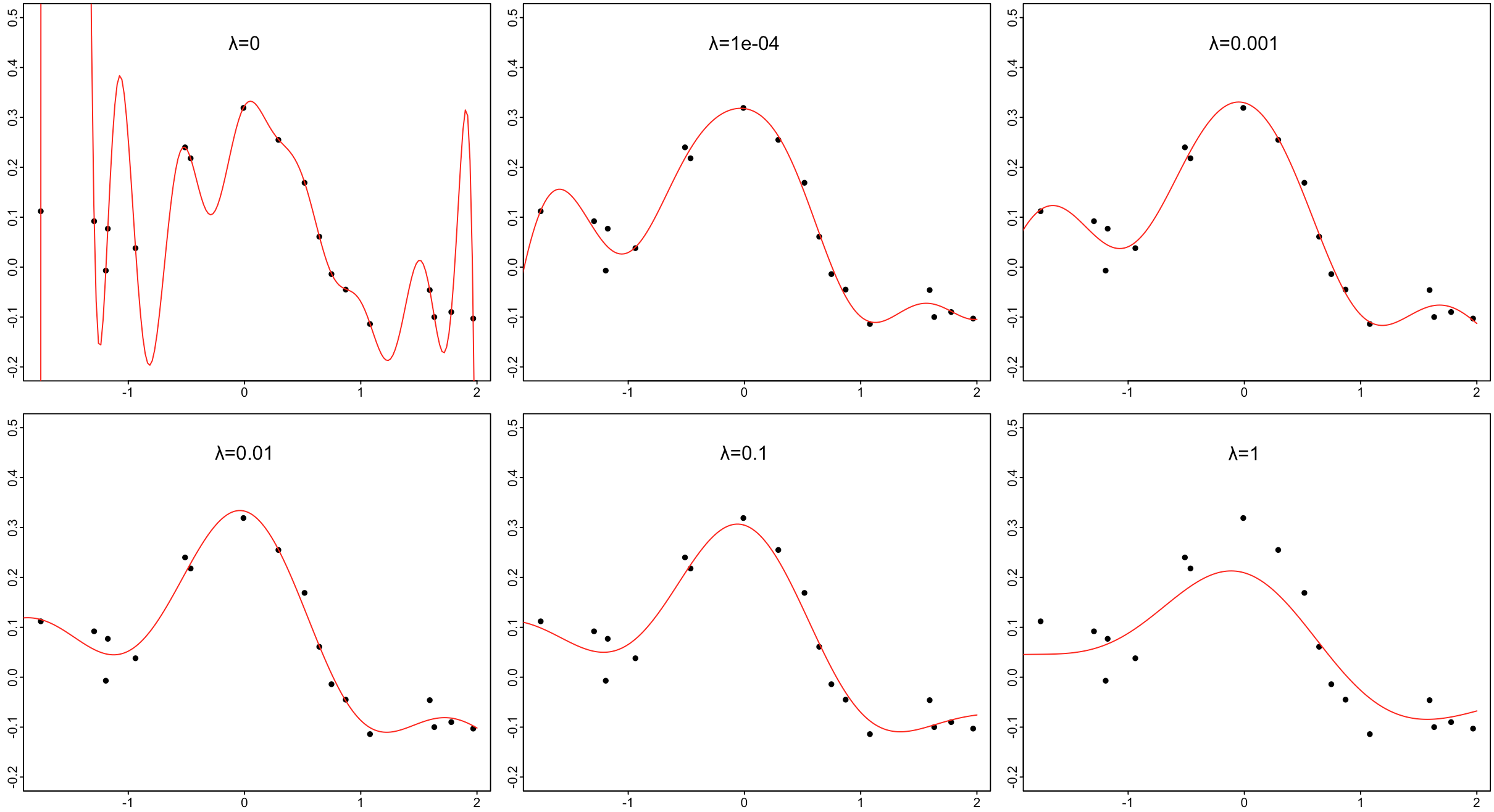
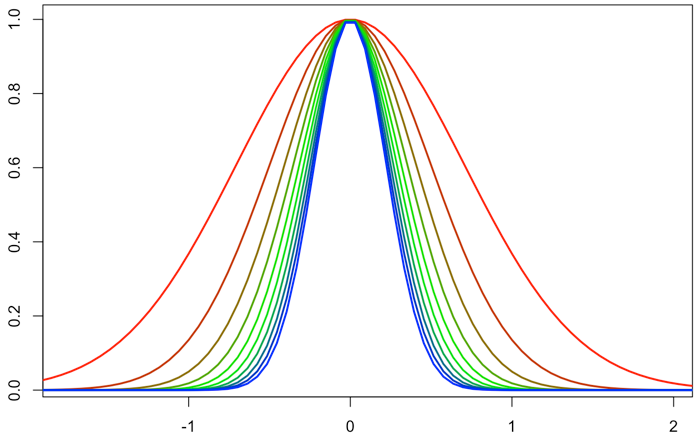
先に図1.2からいきます。
k(x, x')=exp(-\beta\ ||x-x'||^2)
このカーネル関数を、x-x'を横軸に取って描画する。
# x座標
a <- seq(-3,3, length=100)
# 色の準備
N <- 10
Col <- colorRamp(c("Red","Green","Blue"))
Col1 <- rgb(Col(seq(0, 1, length=N))/255)
plot(a, exp(-a^2), type="n")
for(b in 1:N)
lines(a, exp(-b * a^2), col=Col1[b], lwd=2)
β依存的にトンガっていくのが分かります。
サンプルデータ
続いて図1.1。
見栄えのするサンプルデータの準備は結構ツライ(あるある?)。
こんな風にしました。
最後にround入れて丸めておくのが後々効きます。
set.seed(1)
N <- 18
x <- runif(N,-2,2) # X座標
e <- rnorm(N, 0, 0.03) # 正規誤差
A <- 0.7 # 定義域の真ん中だけ凸にしたい
y <- rep(0, N)
y[abs(x)<A] <- -0.5*x[abs(x) < A]^2+0.3
y <- round(y -0.05*x + e, 3)

カーネル関数を使った近似
超短縮版で要約します。
線形回帰と同じイメージから入ります。
所与のデータ集合(X, Y)に対して、関数y=f(x)で近似する。
そのために誤差Y-f(X)の2乗の総和を最小化できる回帰係数を求める。
カーネル関数を使った近似では、このf(x)が特殊な形をしている。
回帰係数をα_1~nとして、
f(x)=\sum_{j=1}^n α_j\ k(X_j, x)
N個$全て$を考慮している、というのがミソです。
2乗誤差の総和は、
\begin{eqnarray}
R_k(α)&=&\sum_{i=1}^n\Big(Y_i-\sum_{j=1}^n α_j\ k(X_j, X_i)\Big)^2 \\
&=&(Y-Kα)^T(Y-Kα)
\end{eqnarray}
ただし、
K_{ij}=k(X_i, X_j)
この2乗誤差の総和を最小化するαは、
α=(K^TK)^{-1}K^TY=K^{-1}Y
と書ける。ので、これを元にf(x)を描けばよろしい。
ただしこれだと、(X, Y)を100%フィットさせた関数になるので、過学習になりがち。なので、$正則化$項目を入れる。
α=(K+λE)^{-1}Y
Eは単位行列。λで調整する。
行列Kを求める。
Yを丸めておかないと、solveでラリる。
データ点の数が18という微妙な数なのも、このせい。
K <- matrix(0, N, N)
for(i in 1:N)
for(j in 1:N)
K[i, j] <- exp(-(x[i] - x[j])^2)
λを決めればαが決まる。
lamda <- `hoge`
alpha <- solve(K+ lambda*diag(N)) %*% y
回帰曲線を構成する(x_k,y_k)は、こんな感じになる。
x_k <- seq(-2, 2, length=200)
y_k <- 0
for(i in 1:N){
y_k <- y_k + alpha[i] * exp(-(x[i] - x_k[k])^2)
}
手を動かすと、大分イメージが湧くと思います。
enjoy!!